立体几何的计算与位置关系课件-2022届高三数学二轮复习(共22张PPT)
文档属性
| 名称 | 立体几何的计算与位置关系课件-2022届高三数学二轮复习(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 10:20:45 | ||
图片预览







文档简介
(共22张PPT)
高三二轮复习
《立体几何中的计算与位置关系》
1
3
4
2
空间几何体的表面积、体积问题
简单的动态问题
空间点、线、面位置关系的判定
空间角的计算
考点1:空间几何体的
表面积与体积
【例1】《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体,如图所示,四边形ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则该几何体的表面积为( )
A. B. 8+
C. + D. 8+ +
B
E
F
B
A
C
D
P
Q
求解几何体的表面积与体积的技巧
等体积转化
三棱锥体积
常用分割或补形的方法
不规则几何体体积
空间问题平面化
求表面积
考点2:多面体与球的切、接问题
【例2】(1)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )
A.4π B. C.6π D.
B
A
B
C
A1
B1
C1
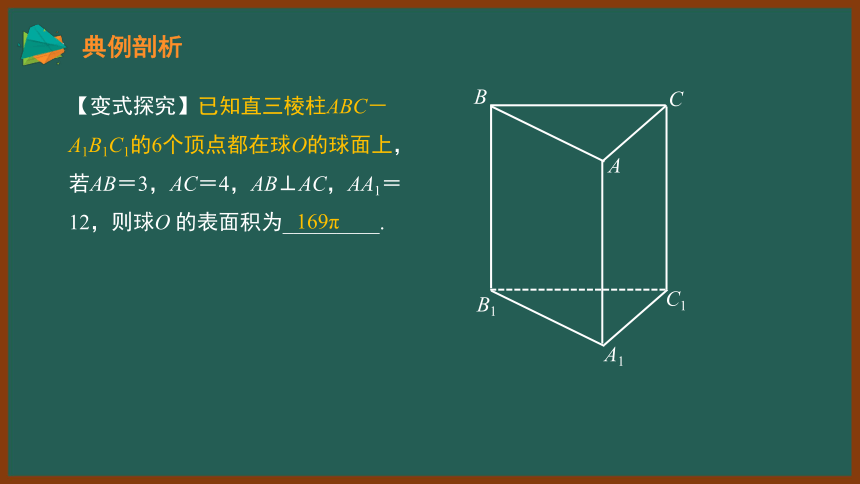
【变式探究】已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O 的表面积为_________.
B
A
C
B1
A1
C1
169π
B
A
S
C
O
【例2】(2)已知三棱锥S -ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S- ABC的体积为9,则球O的表面积为________.
36π
与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常是作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.
若球面上四点P,A,B,C中, PA,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接问题.
考点3:空间平行、垂直关系的判断
【例3】(1)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A
B
C
D
A
【例3】(2)已知m,n,l是互不重合的三条直线,α,β是两个不重合的平面,给出以下四个命题:
①若m,n是异面直线,m α,n β,且m∥β,n∥α,则α∥β;
②若m α,n∩α=A,且点A m,则m,n是异面直线;
③若m,n是异面直线,m∥α,n∥α,且l⊥m,l⊥n,则l⊥α;
④若m⊥α,n β,α⊥β,则m∥n.
其中为真命题的序号是________.(把所有真命题的序号都填上)
①②③
判断与空间位置关系有关命题真假的方法
借助空间几何模型,如从长方体模型、四面体模型等模型中观察线面位置关系,结合有关定理,进行肯定或否定.
02
借助反证法,当从正面入手较难时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断.
03
借助空间线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理进行判断.
01
考点4:简单的动态问题
【例4】(1)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′ -CD -B的平面角为α,则( )
A.∠A′DB≤α
B. ∠A′DB≥α
C. ∠A′CB≤α
D. ∠A′CB≥α
A
C
A′
D
B
【例4】(1)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′ -CD -B的平面角为α,则( )
A.∠A′DB≤α
B. ∠A′DB≥α
C. ∠A′CB≤α
D. ∠A′CB≥α
A
C
A′
D
B
H
B
【例4】(2)如图,M,N分别是棱长为1的正方体ABCD- A1B1C1D1的棱AA1,BC上两动点,且MN=,则线段MN的中点P的轨迹是( )
A.一条线段
B.一段圆弧
C.一个球面区域
D.两条平行线段
M
N
A
D
C
B
A1
B1
C1
D1
P
B
对于立体几何中的动态问题,关键是抓住变化过程中不变的位置关系和数量关系,事实上动静是相对的,以静制动是处理立体几何中动态元素的良策.
1
解此类问题还要回归到最本质的定义、定理、性质或现有结论中.
2
求解几何体的表面积或体积
对于不规则几何体,可采用割补法求解;对于某些三棱锥,有时可采用等体积转换法求解.
对于规则几何体,可直接利用公式计算.
求解旋转体的表面积和体积时,注意圆柱的轴截面是矩形,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形的应用.
求解几何体的表面积时要注意:
S表=S侧+S底.
球的简单组合体中几何体度量之间的关系,如棱长为a的正方体的外接球、内切球、棱切球的半径分别为, , .
锥体体积公式为V= Sh,在求解锥体体积中,不能漏掉
空间中点、线、面的位置关系的判定
可以从线、面的概念、定理出发,学会找特例、反例.
可以借助长方体,在理解空间点、线、面位置关系的基础上,抽象出空间线、面的位置关系的定义.
再见!
高三二轮复习
《立体几何中的计算与位置关系》
1
3
4
2
空间几何体的表面积、体积问题
简单的动态问题
空间点、线、面位置关系的判定
空间角的计算
考点1:空间几何体的
表面积与体积
【例1】《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体,如图所示,四边形ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则该几何体的表面积为( )
A. B. 8+
C. + D. 8+ +
B
E
F
B
A
C
D
P
Q
求解几何体的表面积与体积的技巧
等体积转化
三棱锥体积
常用分割或补形的方法
不规则几何体体积
空间问题平面化
求表面积
考点2:多面体与球的切、接问题
【例2】(1)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )
A.4π B. C.6π D.
B
A
B
C
A1
B1
C1
【变式探究】已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O 的表面积为_________.
B
A
C
B1
A1
C1
169π
B
A
S
C
O
【例2】(2)已知三棱锥S -ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S- ABC的体积为9,则球O的表面积为________.
36π
与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常是作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.
若球面上四点P,A,B,C中, PA,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接问题.
考点3:空间平行、垂直关系的判断
【例3】(1)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A
B
C
D
A
【例3】(2)已知m,n,l是互不重合的三条直线,α,β是两个不重合的平面,给出以下四个命题:
①若m,n是异面直线,m α,n β,且m∥β,n∥α,则α∥β;
②若m α,n∩α=A,且点A m,则m,n是异面直线;
③若m,n是异面直线,m∥α,n∥α,且l⊥m,l⊥n,则l⊥α;
④若m⊥α,n β,α⊥β,则m∥n.
其中为真命题的序号是________.(把所有真命题的序号都填上)
①②③
判断与空间位置关系有关命题真假的方法
借助空间几何模型,如从长方体模型、四面体模型等模型中观察线面位置关系,结合有关定理,进行肯定或否定.
02
借助反证法,当从正面入手较难时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断.
03
借助空间线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理进行判断.
01
考点4:简单的动态问题
【例4】(1)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′ -CD -B的平面角为α,则( )
A.∠A′DB≤α
B. ∠A′DB≥α
C. ∠A′CB≤α
D. ∠A′CB≥α
A
C
A′
D
B
【例4】(1)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′ -CD -B的平面角为α,则( )
A.∠A′DB≤α
B. ∠A′DB≥α
C. ∠A′CB≤α
D. ∠A′CB≥α
A
C
A′
D
B
H
B
【例4】(2)如图,M,N分别是棱长为1的正方体ABCD- A1B1C1D1的棱AA1,BC上两动点,且MN=,则线段MN的中点P的轨迹是( )
A.一条线段
B.一段圆弧
C.一个球面区域
D.两条平行线段
M
N
A
D
C
B
A1
B1
C1
D1
P
B
对于立体几何中的动态问题,关键是抓住变化过程中不变的位置关系和数量关系,事实上动静是相对的,以静制动是处理立体几何中动态元素的良策.
1
解此类问题还要回归到最本质的定义、定理、性质或现有结论中.
2
求解几何体的表面积或体积
对于不规则几何体,可采用割补法求解;对于某些三棱锥,有时可采用等体积转换法求解.
对于规则几何体,可直接利用公式计算.
求解旋转体的表面积和体积时,注意圆柱的轴截面是矩形,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形的应用.
求解几何体的表面积时要注意:
S表=S侧+S底.
球的简单组合体中几何体度量之间的关系,如棱长为a的正方体的外接球、内切球、棱切球的半径分别为, , .
锥体体积公式为V= Sh,在求解锥体体积中,不能漏掉
空间中点、线、面的位置关系的判定
可以从线、面的概念、定理出发,学会找特例、反例.
可以借助长方体,在理解空间点、线、面位置关系的基础上,抽象出空间线、面的位置关系的定义.
再见!
同课章节目录
