2022届高三数学二轮复习坐标法解决立体几何问题课件(39张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习坐标法解决立体几何问题课件(39张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 626.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 10:02:29 | ||
图片预览






文档简介
(共39张PPT)
坐标法解决立体几何问题
向量方法的前提
------建立空间直角坐标系
右手系
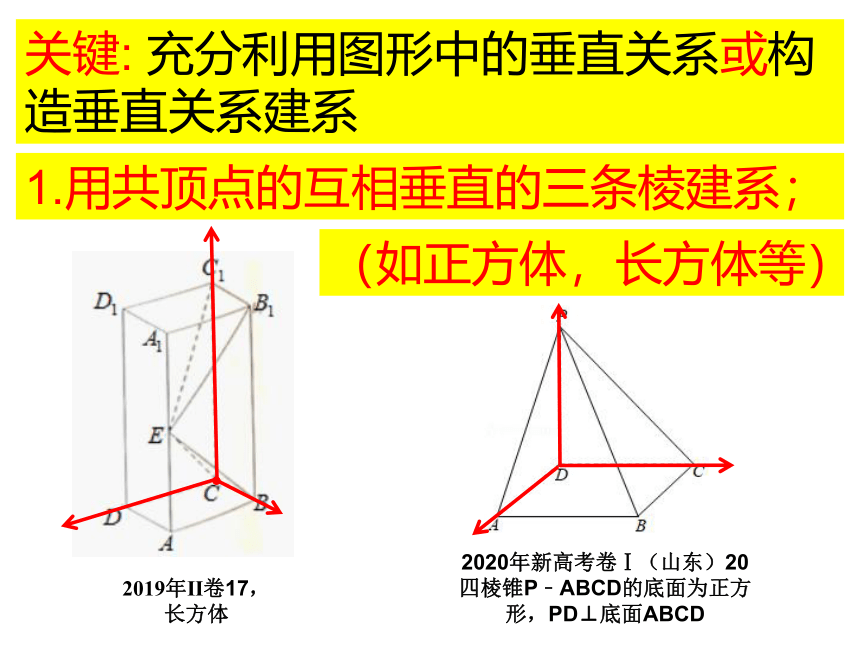
关键: 充分利用图形中的垂直关系或构造垂直关系建系
1.用共顶点的互相垂直的三条棱建系;
(如正方体,长方体等)
2019年Ⅱ卷17,
长方体
2020年新高考卷Ⅰ(山东)20
四棱锥P﹣ABCD的底面为正方形,PD⊥底面ABCD
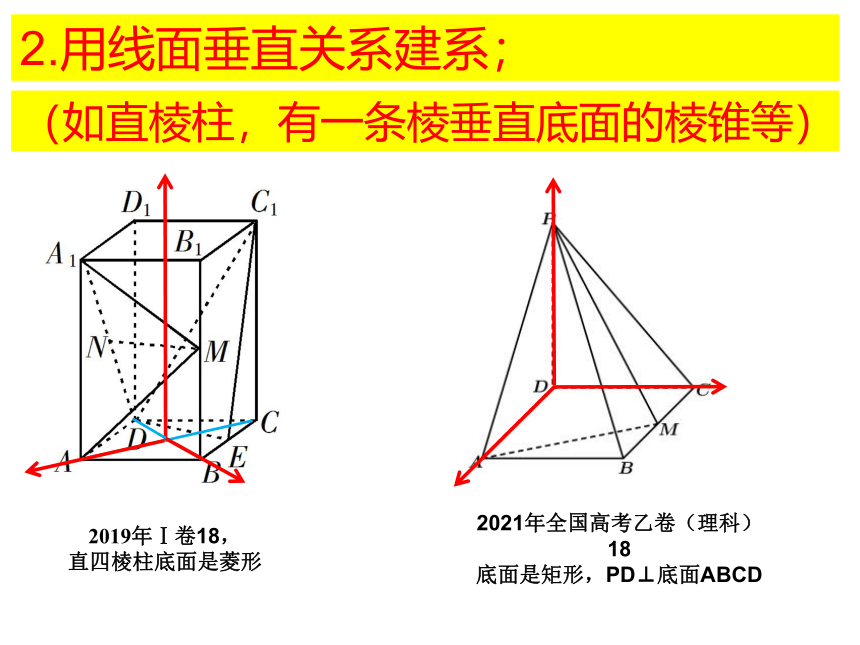
2.用线面垂直关系建系;
(如直棱柱,有一条棱垂直底面的棱锥等)
2019年Ⅰ卷18,
直四棱柱底面是菱形
2021年全国高考乙卷(理科)18
底面是矩形,PD⊥底面ABCD
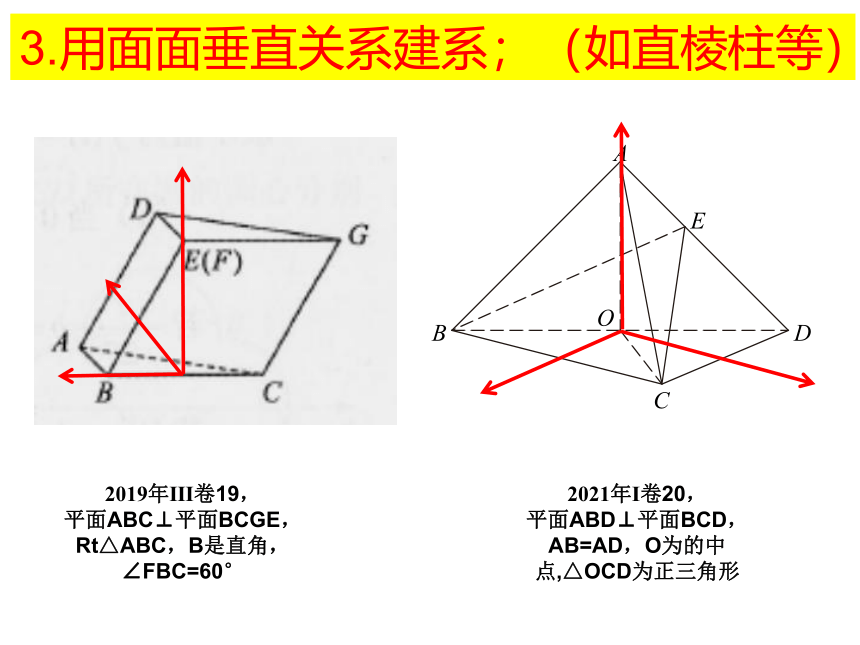
3.用面面垂直关系建系;(如直棱柱等)
2019年Ⅲ卷19,
平面ABC⊥平面BCGE,Rt△ABC,B是直角,∠FBC=60°
2021年Ⅰ卷20,
平面ABD⊥平面BCD,AB=AD,O为的中点,△OCD为正三角形
A
P
D
C
B
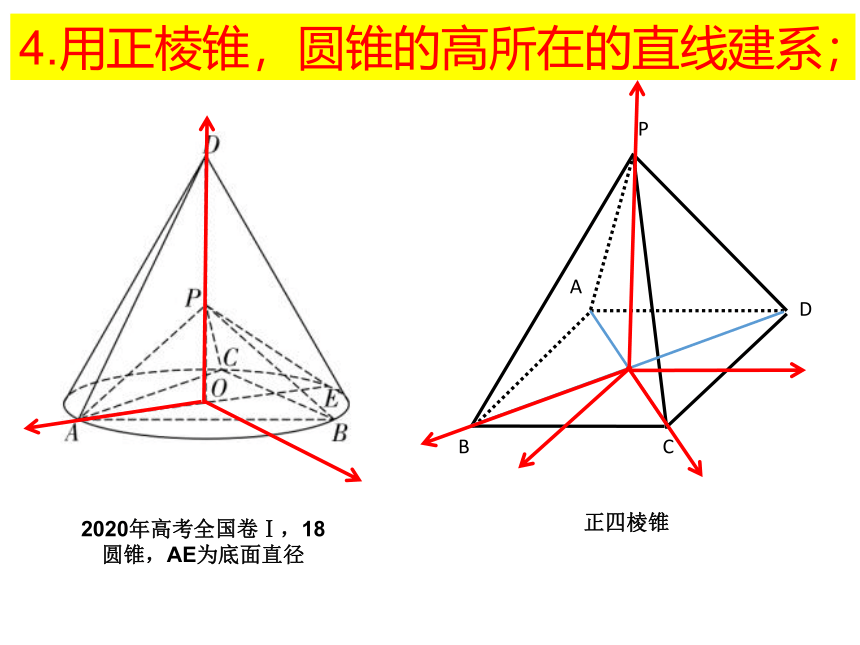
4.用正棱锥,圆锥的高所在的直线建系;
2020年高考全国卷Ⅰ,18
圆锥,AE为底面直径
正四棱锥
注意:1.不能凭感觉建系,
要有严格的证明过程;
2.对于复杂不规则几何体,要先找垂直,或者构造垂直建系;
3.要建立右手系,尽可能使更多的点在坐标轴上或坐标平面上;
向量方法的准备
------找点的坐标
向量方法的准备
------两个重要向量
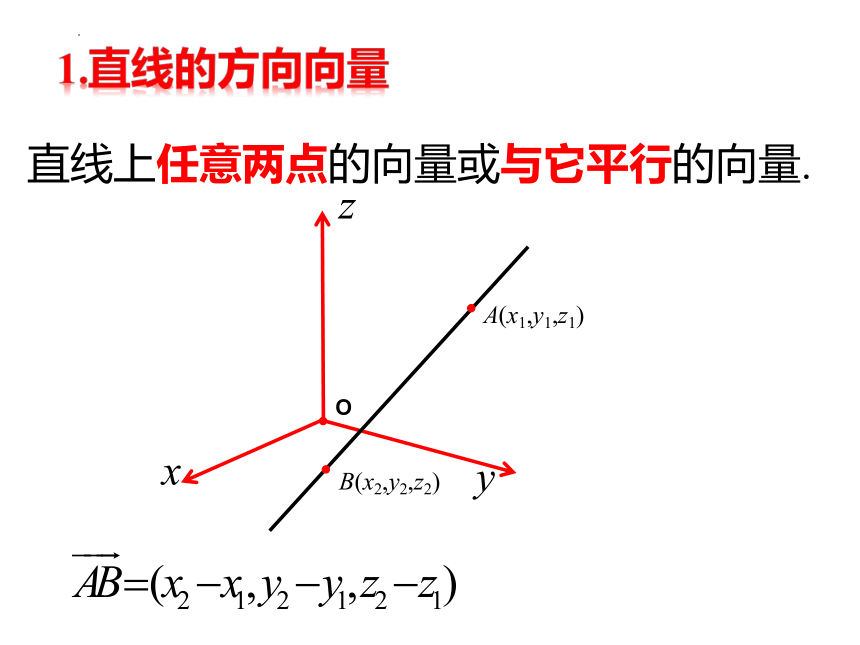
直线的方向向量
平面的法向量
直线上任意两点的向量或与它平行的向量.
1.直线的方向向量
A(x1,y1,z1)
B(x2,y2,z2)
O
x
y
z
α
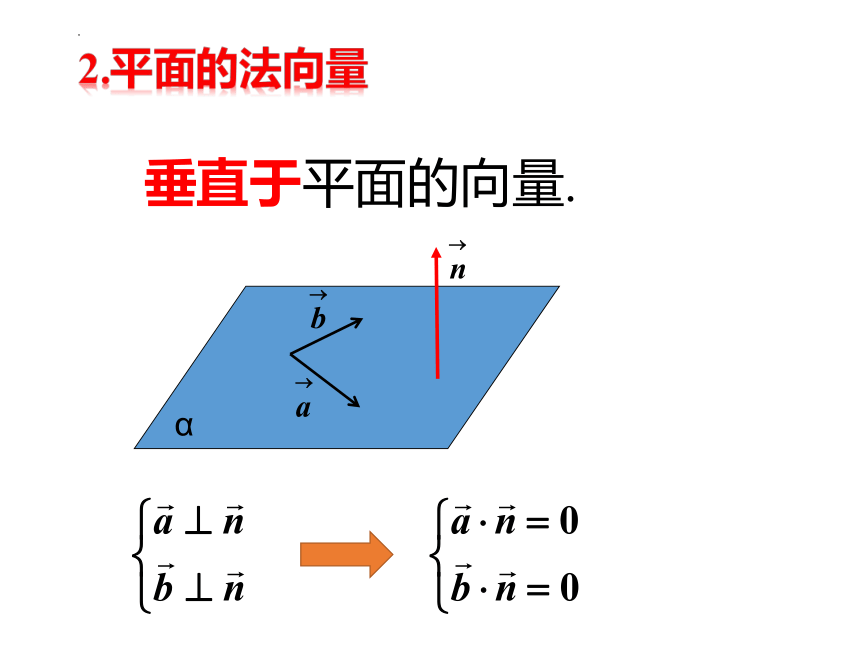
2.平面的法向量
垂直于平面的向量.
求平面的法向量的坐标的一般步骤:
第一步(设):设出平面法向量的坐标为n=(x,y,z).
第二步(列):根据n·a = 0且n·b = 0可列出方程组
第三步(解):把z看作常数,用z表示x、y.
第四步(取):取z为任意一个正数(当然取得越特殊越好),便得到平面法向量n的坐标.
例1.在棱长为2的正方体ABCD-A1B1C1D1中,O是面AC的中心,求面OA1D1的法向量.
A
A
A
B
C
D
O
A1
B1
C1
D1
z
x
y
立体几何中的向量方法
------空间位置问题
例2.棱长都等于2的正三棱柱ABC-A1B1C1,
D,E分别是AC,CC1的中点,求证:
(1)A1E ⊥平面DBC1;
(2)AB1 ∥ 平面DBC1
A1
C1
B1
A
C
B
E
D
z
x
y
立体几何中的向量方法
------空间角问题
①求出两条异面直线的方向向量;
②套公式求两方向向量的夹角的余弦值;则两直线的夹角与其相等或互补,我们仅取锐角或直角就行了.
1.异面直线所成角
P
2.直线与平面所成角
3.二面角
立体几何中的向量方法
------距离问题
一、求点到平面的距离
一般方法:
利用定义先作出过这个点到平面的垂线段,再计算这个垂线段的长度。
还可以用等积法求距离.
向量法求点到平面的距离
其中 为斜向量, 为法向量。
二、直线到平面的距离
其中 为斜向量, 为法向量。
l
三、平面到平面的距离
四、异面直线的距离
注意:
是与 都垂直的向量
点到平面的距离:
直线到平面的距离:
平面到平面的距离:
异面直线的距离:
四种距离的统一向量形式:
例题6
(1) 求B1到面A1BE的距离;
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:
例题6
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:
(2) 求D1C到面A1BE的距离;
例题6
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:
(3) 求面A1DB与面D1CB1的距离;
例题6
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:
(4) 求异面直线D1B与A1E的距离.
F
E
B1
C1
D1
D
C
A
练习1:
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是B1C1和C1D1 的中点,求点A1到平面DBEF的距离。
B
x
y
z
A1
练习2:
已知棱长为1的正方体ABCD-A1B1C1D1,求平面DA1C1和平面AB1C间的距离。
B1
C1
D1
D
C
A
B
x
y
z
A1
练习3:
已知棱长为1的正方体ABCD-A1B1C1D1,求直线DA1和AC间的距离。
B1
C1
D1
D
C
A
B
x
y
z
A1
小结
利用法向量来解决上述立体几何题目,最大的优点就是不用象在进行几何推理时那样去确定垂足的位置,完全依靠计算就可以解决问题。但是也有局限性,用代数推理解立体几何题目,关键就是得建立空间直角坐标系,把向量通过坐标形式表示出来,所以能用这种方法解题的立体几何模型一般都是如:正(长)方体、直棱柱、正棱锥等。
坐标法解决立体几何问题
向量方法的前提
------建立空间直角坐标系
右手系
关键: 充分利用图形中的垂直关系或构造垂直关系建系
1.用共顶点的互相垂直的三条棱建系;
(如正方体,长方体等)
2019年Ⅱ卷17,
长方体
2020年新高考卷Ⅰ(山东)20
四棱锥P﹣ABCD的底面为正方形,PD⊥底面ABCD
2.用线面垂直关系建系;
(如直棱柱,有一条棱垂直底面的棱锥等)
2019年Ⅰ卷18,
直四棱柱底面是菱形
2021年全国高考乙卷(理科)18
底面是矩形,PD⊥底面ABCD
3.用面面垂直关系建系;(如直棱柱等)
2019年Ⅲ卷19,
平面ABC⊥平面BCGE,Rt△ABC,B是直角,∠FBC=60°
2021年Ⅰ卷20,
平面ABD⊥平面BCD,AB=AD,O为的中点,△OCD为正三角形
A
P
D
C
B
4.用正棱锥,圆锥的高所在的直线建系;
2020年高考全国卷Ⅰ,18
圆锥,AE为底面直径
正四棱锥
注意:1.不能凭感觉建系,
要有严格的证明过程;
2.对于复杂不规则几何体,要先找垂直,或者构造垂直建系;
3.要建立右手系,尽可能使更多的点在坐标轴上或坐标平面上;
向量方法的准备
------找点的坐标
向量方法的准备
------两个重要向量
直线的方向向量
平面的法向量
直线上任意两点的向量或与它平行的向量.
1.直线的方向向量
A(x1,y1,z1)
B(x2,y2,z2)
O
x
y
z
α
2.平面的法向量
垂直于平面的向量.
求平面的法向量的坐标的一般步骤:
第一步(设):设出平面法向量的坐标为n=(x,y,z).
第二步(列):根据n·a = 0且n·b = 0可列出方程组
第三步(解):把z看作常数,用z表示x、y.
第四步(取):取z为任意一个正数(当然取得越特殊越好),便得到平面法向量n的坐标.
例1.在棱长为2的正方体ABCD-A1B1C1D1中,O是面AC的中心,求面OA1D1的法向量.
A
A
A
B
C
D
O
A1
B1
C1
D1
z
x
y
立体几何中的向量方法
------空间位置问题
例2.棱长都等于2的正三棱柱ABC-A1B1C1,
D,E分别是AC,CC1的中点,求证:
(1)A1E ⊥平面DBC1;
(2)AB1 ∥ 平面DBC1
A1
C1
B1
A
C
B
E
D
z
x
y
立体几何中的向量方法
------空间角问题
①求出两条异面直线的方向向量;
②套公式求两方向向量的夹角的余弦值;则两直线的夹角与其相等或互补,我们仅取锐角或直角就行了.
1.异面直线所成角
P
2.直线与平面所成角
3.二面角
立体几何中的向量方法
------距离问题
一、求点到平面的距离
一般方法:
利用定义先作出过这个点到平面的垂线段,再计算这个垂线段的长度。
还可以用等积法求距离.
向量法求点到平面的距离
其中 为斜向量, 为法向量。
二、直线到平面的距离
其中 为斜向量, 为法向量。
l
三、平面到平面的距离
四、异面直线的距离
注意:
是与 都垂直的向量
点到平面的距离:
直线到平面的距离:
平面到平面的距离:
异面直线的距离:
四种距离的统一向量形式:
例题6
(1) 求B1到面A1BE的距离;
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:
例题6
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:
(2) 求D1C到面A1BE的距离;
例题6
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:
(3) 求面A1DB与面D1CB1的距离;
例题6
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:
(4) 求异面直线D1B与A1E的距离.
F
E
B1
C1
D1
D
C
A
练习1:
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是B1C1和C1D1 的中点,求点A1到平面DBEF的距离。
B
x
y
z
A1
练习2:
已知棱长为1的正方体ABCD-A1B1C1D1,求平面DA1C1和平面AB1C间的距离。
B1
C1
D1
D
C
A
B
x
y
z
A1
练习3:
已知棱长为1的正方体ABCD-A1B1C1D1,求直线DA1和AC间的距离。
B1
C1
D1
D
C
A
B
x
y
z
A1
小结
利用法向量来解决上述立体几何题目,最大的优点就是不用象在进行几何推理时那样去确定垂足的位置,完全依靠计算就可以解决问题。但是也有局限性,用代数推理解立体几何题目,关键就是得建立空间直角坐标系,把向量通过坐标形式表示出来,所以能用这种方法解题的立体几何模型一般都是如:正(长)方体、直棱柱、正棱锥等。
同课章节目录
