北师大版九下数学 第三章圆综合试题 (word版含答案)
文档属性
| 名称 | 北师大版九下数学 第三章圆综合试题 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 300.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 07:26:42 | ||
图片预览


文档简介
圆综合试题
一、单选题
1.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
2.已知⊙O的半径为6cm,圆心O到直线a的距离为6cm,则直线a与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
3.如图,已知四边形 内接于 , ,则 的度数是( )。
A. B. C. D.
4.同一平面内, 一个点到圆的最小距离为 , 最大距离为 , 则该圆的半径为 ( )
A. 或 B. 或
C. 或 D. 或
5.如图所示,⊙O的半径为5,点O到直线l的距离为7,P是直线l上的一个动点,PQ与⊙O相切于点Q.则PQ的最小值为( )
A. B. C.2 D.2
6.如图,的内切圆与分别相切于点D,E,F,若,则的度数是( )
A. B. C. D.
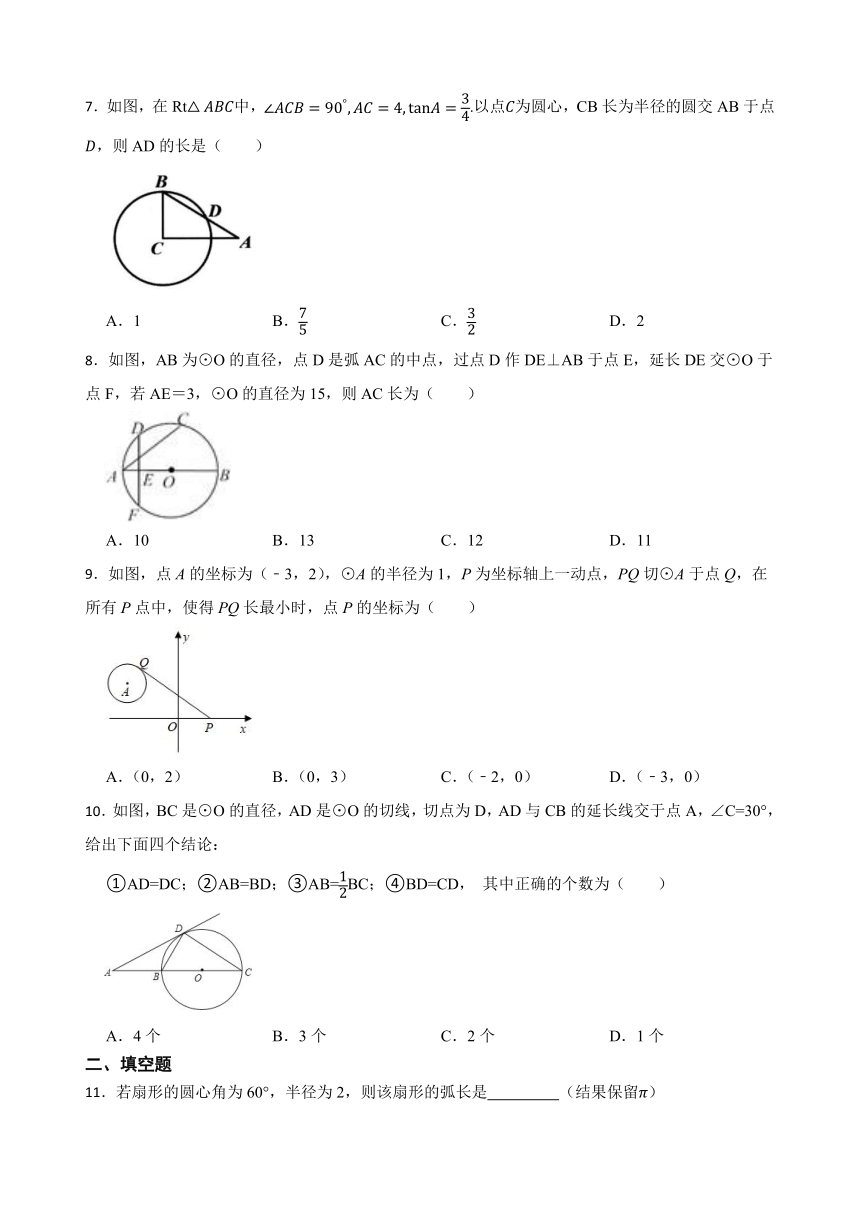
7.如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点,则AD的长是( )
A.1 B. C. D.2
8.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙O的直径为15,则AC长为( )
A.10 B.13 C.12 D.11
9.如图,点A的坐标为(﹣3,2),⊙A的半径为1,P为坐标轴上一动点,PQ切⊙A于点Q,在所有P点中,使得PQ长最小时,点P的坐标为( )
A.(0,2) B.(0,3) C.(﹣2,0) D.(﹣3,0)
10.如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB=BC;④BD=CD, 其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.若扇形的圆心角为60°,半径为2,则该扇形的弧长是 (结果保留)
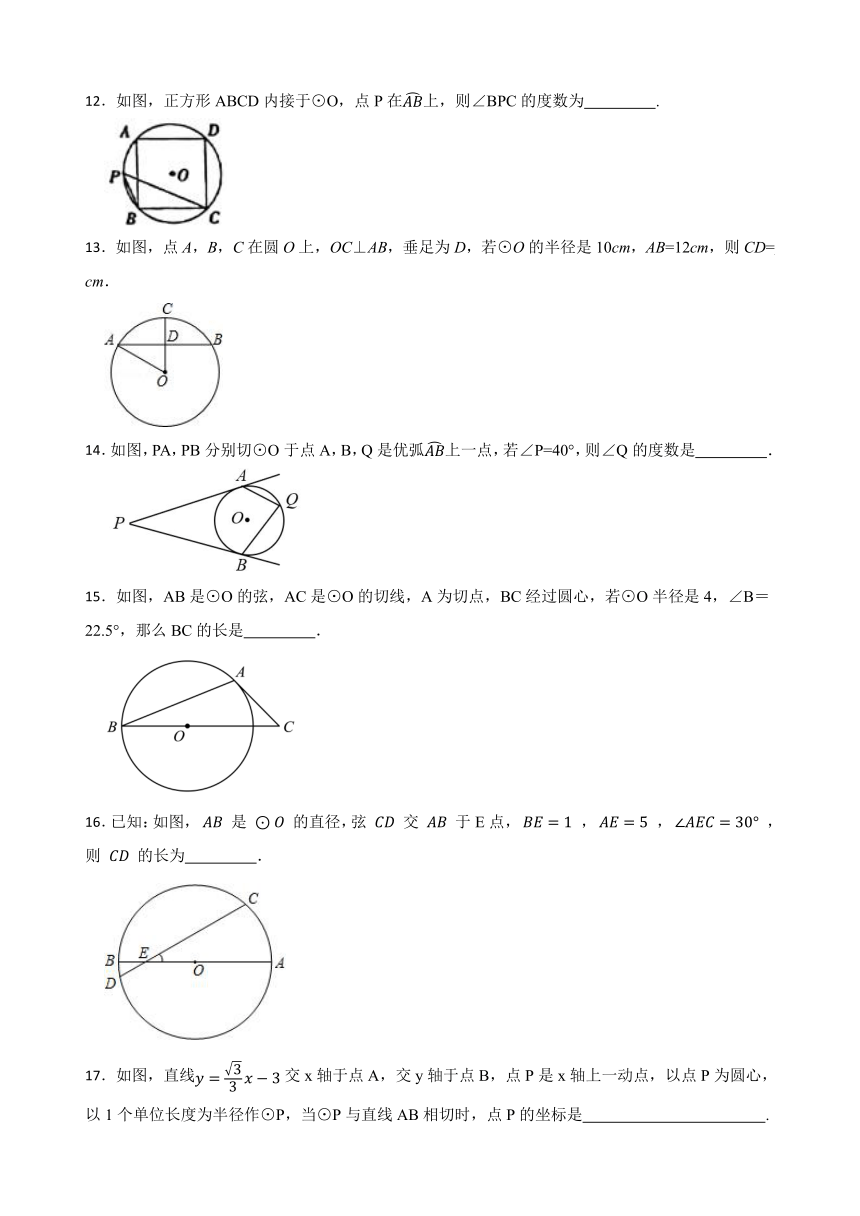
12.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为 .
13.如图,点A,B,C在圆O上,OC⊥AB,垂足为D,若⊙O的半径是10cm,AB=12cm,则CD= cm.
14.如图,PA,PB分别切⊙O于点A,B,Q是优弧上一点,若∠P=40°,则∠Q的度数是 .
15.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若⊙O半径是4,∠B=22.5°,那么BC的长是 .
16.已知:如图, 是 的直径,弦 交 于E点, , , ,则 的长为 .
17.如图,直线交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是 .
18.如图,半径为 的 中, 为直径,弦 且过半径 的中点,点 为 上一动点, 于点 .当点 从点 出发顺时针运动到点 时,点 所经过的路径长为 .
三、解答题
19.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于点 D,BC于点E,连接ED.求证:ED=EC.
20.如图为桥洞的形状,其正视图是由 和矩形ABCD构成.O点为 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求 所在⊙O的半径DO.
21.将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,求图中阴影部分的面积.
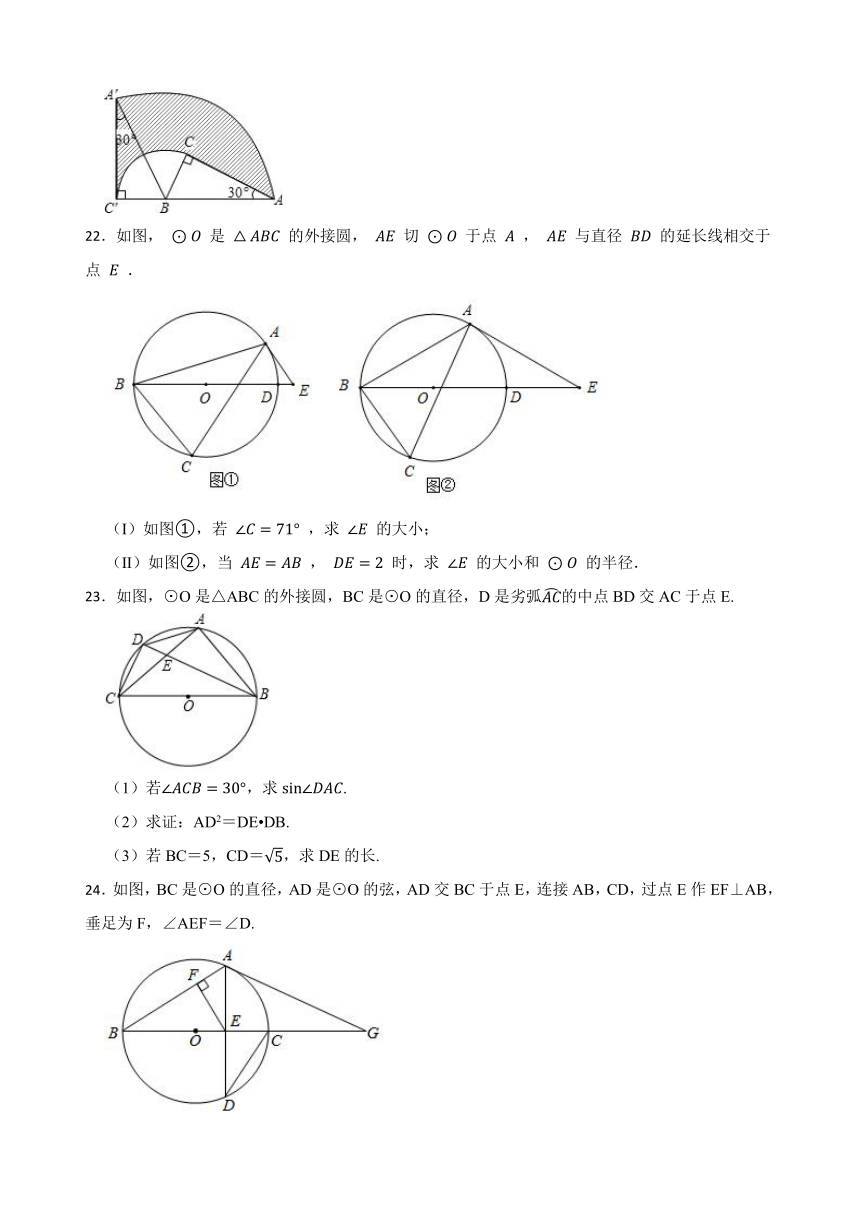
22.如图, 是 的外接圆, 切 于点 , 与直径 的延长线相交于点 .
(Ⅰ)如图①,若 ,求 的大小;
(Ⅱ)如图②,当 , 时,求 的大小和 的半径.
23.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧的中点BD交AC于点E.
(1)若,求.
(2)求证:AD2=DE DB.
(3)若BC=5,CD=,求DE的长.
24.如图,BC是⊙O的直径,AD是⊙O的弦,AD交BC于点E,连接AB,CD,过点E作EF⊥AB,垂足为F,∠AEF=∠D.
(1)求证:AD⊥BC;
(2)点G在BC的延长线上,连接AG,∠DAG=2∠D.
①求证:AG与⊙O相切;
②当 ,CE=4时,直接写出CG的长.
答案解析部分
1.【答案】B
【解析】【解答】如图,取AB的中点O,分别连接OC、OB,则OC⊥AB,且
在Rt△OBC中,OB=5,由勾股定理得:
点P线段BC上,则,即
由对称性,当点P在线段AC上时,
∴当点P在弦AB上时,
∵
∴选项B符合题意
故答案为:B
【分析】先作辅助线,取AB的中点O,分别连接OC、OB,取AB的中点O,根据垂径定理得OC⊥AB,且,然后在Rt△OBC中由勾股定理得OC=4,再由垂线段最短可得答案。
2.【答案】B
【解析】【解答】解:设圆心O到直线a的距离为d,则d=6 cm
∵⊙O的半径为6 cm,
即半径=d=6 cm,
∴直线a与⊙O的位置关系是相切.
故答案为:B.
【分析】由⊙O的半径为6cm,圆心O到直线a的距离d=6cm,根据直线与圆的位置关系判定方法:当d>r时,直线与圆相离,当d<r时,直线与圆相交,当d=r时,直线与圆相切,即可判断.
3.【答案】B
【解析】【解答】解:∵四边形ABCD为圆内接四边形,
∴∠ADC=180°-∠ABC=180°-70°=110°.
故答案为:B.
【分析】利用圆内接四边形的对角互补的性质列式计算即可.
4.【答案】C
【解析】【解答】解:分为两种情况:
①当点P在圆内时,最近点的距离为6cm,最远点的距离为8cm,则直径是14cm,因而半径是7cm;
②当点P在圆外时,最近点的距离为6cm,最远点的距离为8cm,则直径是2cm,因而半径是1cm.
故答案为:C.
【分析】①当点P在圆内时,直径是14cm,据此可得半径;②当点P在圆外时,直径是2cm,据此可得半径.
5.【答案】C
【解析】【解答】解:∵PQ与⊙O相切于点Q,
∴OQ⊥PQ,
∴PQ2=OP2-OQ2=OP2-52=OP2-25,
∴当OP最小时,PQ有最小值,
∵点O到直线l的距离为7,
∴OP的最小值为7,
∴PQ的最小值=,
故答案为:C.
【分析】由切线的性质可得OQ⊥PQ,由勾股定理可得PQ2=OP2-OQ2=OP2-52=OP2-25,所以可得当OP最小时,PQ有最小值,由于OP的最小值为7,从而得解.
6.【答案】D
【解析】【解答】解:连接OD、OF,如图所示:
∵△ABC的内切圆与AB、BC、AC分别相切于点D,E,F,,
∴,
∴;
故答案为:D.
【分析】连接OD、OF,根据切线的性质可得∠ADO=∠AFO=90°,由同弧所对的圆心角等于圆周角的2倍可得∠DOF=2∠DEF=100°,然后根据四边形内角和为360°进行计算.
7.【答案】B
【解析】【解答】解:连接CD,过点C作CE⊥AB于点E,
在Rt△ABC中,
解之:BC=3,
∴
∵
∴3×4=5CE
解之:CE=.
∴
∴BD=2BE=
∴.
故答案为:B.
【分析】连接CD,过点C作CE⊥AB于点E,利用解直角三角形求出BC的长,利用勾股定理求出AB的长;再利用三角形的面积公式求出CE的长;然后利用勾股定理求出BE的长,根据BD=2BE可求出BD的长;然后根据AD=AB-BD,代入计算求出AD的长.
8.【答案】C
【解析】【解答】解:如图,连接AD,BD,
∵点D是弧AC的中点,DE⊥AB于点E,
∴,∠AED=∠DEB=90°,DF=2DE,
∴∠ADE=∠B,AC=DF,
∴△AED∽△DEB,
∴,
∴DE2=AE·BE=3×(15-3)=36,
∴DE=6,
∴DF=2DE=12,
∴AC=DF=12.
故答案为:C.
【分析】连接AD,BD,根据垂径定理和圆周角定理得出∠ADE=∠B,DF=2DE,再根据等弧所对的弦相等得出AC=DF,利用相似三角形的判定与性质得出DE=6,从而得出DF=12,即可得出AC=12.
9.【答案】D
【解析】【解答】解:连接AQ、PA,如图,
∵PQ切⊙A于点Q,
∴AQ⊥PQ,
∴∠AQP=90°,
∴PQ= ,
当AP的长度最小时,PQ的长度最小,
∵AP⊥x轴时,AP的长度最小,
∴AP⊥x轴时,PQ的长度最小,
∵A(﹣3,2),
∴此时P点坐标为(﹣3,0).
故答案为:D.
【分析】先求出PQ= ,再根据点A的坐标求解即可。
10.【答案】B
【解析】【解答】连接DO,∵BC是⊙O的直径,AD是⊙O的切线,切点为D,∴∠BDC=∠ADO=90°,∵DO=CO,∴∠C=∠CDO=30°,∴∠A=30°,∠DBC=60°,
∠ADB=30°,∴AD=DC,故①正确;∵∠A=30°,∠DBC=60°,∴∠ADB=30°,∴AB=BD,故②正确;∵∠C=30°,∠BDC=90°,∴BD=BC,∵AB=BD,
∴AB=BC,故③正确;无法得到BD=CD,故④错误.故选:B
【分析】利用圆周角定理结合切线的性质得出∠BDC=∠ADO=90°,进而得出∠A,∠ADB的度数即可得出答案,再利用直角三角形中30°所对的边等于斜边的一半进而得出AB=BC,判断即可.
11.【答案】
【解析】【解答】解:依题意,n=,r=2,
∴扇形的弧长=.
故答案为:.
【分析】利用弧长公式计算即可.
12.【答案】45°
【解析】【解答】解:连接OB、OC,
∵四边形ABCD是正方形,
∴∠BOC=90°,
∴∠BPC=.
故答案为:45°.
【分析】连接OB、OC,由正方形的性质可得∠BOC=90°,然后根据圆周角定理进行解答.
13.【答案】2
【解析】【解答】解:∵OC是⊙O的半径且OC⊥AB,垂足为D,
∴OA=OC=10cm,AD= AB= ×12=6cm,
∵在Rt△AOD中,OA=10cm,AD=6cm,
∴OD= cm,
∴CD=OC﹣OD=10﹣8=2cm.
故答案为2.
【分析】在直角三角形AOD中利用勾股定理求出OD的值,然后利用CD=OC﹣OD即可求解。
14.【答案】70°
【解析】【解答】解:连接OA、OB,
∵PA,PB分别切⊙O于点A,B,
∴∠OAP=∠OBP=90°,又∠P=40°,
∴∠AOB=360°-90°-90°-40°=140°,
∴∠Q=∠AOB=70°,
故答案为:70°.
【分析】连接OA、OB,先根据切线的性质和四边形的内角和求出∠AOB,再利用圆周角的性质可得∠Q=∠AOB=70°。
15.【答案】
【解析】【解答】解:连接,如图,
AC是⊙O的切线,
是等腰直角三角形,
故答案为:
【分析】连接OA,根据,可得是等腰直角三角形,即可得到,再利用线段的和差可得。
16.【答案】
【解析】【解答】解:如图所示,过点O作OF⊥CD于F,连接OD,
∴∠OFE=90°, ,
∵∠AEC=30°,
∴ ,
∵BE=1,AE=5,
∴AB=BE+AE=6,
∵AB是直径,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
故答案为: .
【分析】过点O作OF⊥CD于F,连接OD,根据,可得,在直角△DOF中求得DF的长即可求解。
17.【答案】
【解析】【解答】解:∵直线交x轴于点A,交y轴于点B,
∴令x=0,得y=-3,令y=0,得x=-4,
∴A(,0),B(0.-3),
∴OA=,OB=3,
∴AB=6,
设⊙P与直线AB相切于D,
连接PD,
如图示:
则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴
∴
∴
∴或,
∴P点坐标为:
故答案为:.
【分析】易得A(,0),B(0,-3),然后求出OA、OB、AB,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=1,证明△APD∽△ABO,由相似三角形的性质可得AP,进而求出OP,据此可得点P的坐标.
18.【答案】
【解析】【解答】
点 的路径是以 为半径, 中点为圆心的一段圆弧
如图,连接 ,设 于点 ,连接 的中点 和点 ,
的半径为 ,弦 且过半径 的中点, 为直径
,
,
故答案为: .
【分析】连接AC,AO,由AB⊥CD,利用垂径定理得到G为AB的中点,由中点的定义确定出OG的长,在直角三角形AOG中,由AO与OG的长,利用勾股定理求出AG的长,进而确定出AB的长,由CO+GO求出CG的长,在直角三角形AGC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半圆,如图所示。当E位于点B时,CG⊥AE,此时F、G重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发,顺时针运动到点D时,点F所经过的路径长弧AG,在直角三角形ACG中,利用锐角三角函数定义求出∠ACG的度数,进而确定出弧AG所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出弧AG的长,即可求出点F所经过的路径长。
19.【答案】解:∵AB=AC,
∴∠B=∠C,
∵四边形ABED是圆内接四边形,
∴∠CDE=∠B,
∴∠CDE=∠C,
∴CE=DE.
【解析】【分析】根据等腰三角形的性质和圆内接四边形的性质解答即可;
20.【答案】解:∵OE⊥弦CD于点F,CD为8米,EF为2米,
∴EO垂直平分CD,DF=4m,FO=DO﹣2,在Rt△DFO中,DO2=FO2+DF2,则DO2=(DO﹣2)2+42,解得:DO=5.
答:弧CD所在⊙O的半径DO为5m.
【解析】【分析】根据垂径定理得出EO垂直平分CD,DF=4m,然后利用勾股定理建立方程,求解即可得出OD的长。
21.【答案】解:∵∠BCA=90°,∠BAC=30°,AB=4,∴BC=2,∠CBC′=120°,∠A′BA=120°,
由旋转知△A′BC′≌△ABC ∴ S△A′BC′=S△ABC,
∴S阴影=S△A′BC′+S扇形ABA′-S扇形CBC′-S△ABC= S扇形ABA′-S扇形CBC′= ×(42-22)=4π(cm2).
【解析】【分析】根据图形阴影部分的面积转化为圆心角为 120° ,两个半径分别为4和2的圆环的面积,利用扇形得面积公式求解即可。
22.【答案】解:(Ⅰ)连接 .
∵ 切 于点 ,
∴ ,∴ ,
∵ ,
∴ ,
∴ .
(Ⅱ)连接 ,设 .
∵ ,∴ ,
∵ ,∴ ,
∴ .
∵ 是 的切线,
∴ ,即 ,
在 中, ,
即 ,
解得 ,
∴ .
在 中, ,
∵ ,
∴ ,
∵ ,
∴ ,即 的半径为2.
【解析】【分析】(1)先求出 , 再求出∠AOB=142°,最后求解即可;
(2)先求出 ,再求出 , 最后求解即可。
23.【答案】(1)解:∵BC是⊙O的直径
∴∠CAB=90°
∵
∴∠ABC=90°-30°=60°
∵D是劣弧的中点,得,
∴∠ABD=∠DAC=30°
∴=
(2)证明:由(1)得∠ABD=∠DAC,
又∵∠ADB=∠EDA,
∴△ABD∽△EAD,
∴AD2=DE DB;
(3)解:由D是劣弧的中点,得AD=DC,则DC2=DE DB
∵CB是直径,
∴△BCD是直角三角形.
∴BD=,由DC2=DE DB得,
()2=2DE,
解得:DE=.
【解析】【分析】(1)由圆周角定理可得∠CAB=90°,则∠ABC=90°-∠ACB=60°,根据中点的概念可得,由圆周角定理可得∠ABD=∠DAC=30°,据此求解;
(2)由(1)得∠ABD=∠DAC,证明△ABD∽△EAD,然后由相似三角形的性质证明即可;
(3)根据弧、弦的关系可得AD=DC,则DC2=DE DB,由勾股定理求出BD,然后根据DC2=DE DB就可求出DE.
24.【答案】(1)证明:∵EF⊥AB,
∴∠AFE=90°,
∴∠AEF+∠EAF=90°,
∵∠AEF=∠D,∠ABE=∠D,
∴∠ABE+∠EAF=90°,
∴∠AEB=90°,
∴AD⊥BC
(2)解:①证明:连接OA,AC.
∵AD⊥BC,
∴AE=ED,
∴CA=CD,
∴∠D=∠CAD,
∵∠GAE=2∠D,
∴∠CAG=∠CAD=∠D,
∵OC=OA,
∴∠OCA=∠OAC,
∵∠CEA=90°,
∴∠CAE+∠ACE=90°,
∴∠CAG+∠OAC=90°,
∴OA⊥AG,
∴AG是⊙O的切线.
②解:过点C作CH⊥AG于H.设CG=x,GH=y.
∵CA平分∠GAE,CH⊥AG,CE⊥AE,
∴CH=CE,
∵∠AEC=∠AHC=90°,AC=AC,EC=CH,
∴Rt△ACE≌Rt△ACH(HL),
∴AE=AH,
∵EF⊥AB,BC是直径,
∴∠BFE=∠BAC,
∴EF∥AC,
∴ ,
∵CE=4,
∴BE=10,
∵BC⊥AD,
∴ ,
∴∠CAE=∠ABC,
∵∠AEC=∠AEB=90°,
∴△AEB∽△CEA,
∴ ,
∴AE2=4×10,
∵AE>0,
∴AE= ,
∴AH=AE= ,
∵∠G=∠G,∠CHG=∠AEG=90°,
∴△GHC∽△GEA,
∴ ,
∴ ,
解得x= .
经检验:x= 是原方程的根且符合题意,
【解析】【分析】(1)由垂直的概念可得∠AFE=90°,由圆周角定理可得∠ABE=∠D,结合已知条件可推出∠AEB=90°,据此证明;
(2)①连接OA,AC,由垂径定理可得AE=ED,由等腰三角形的性质可得∠D=∠CAD,∠OCA=∠OAC,结合已知条件可得∠CAG=∠CAD=∠D,推出OA⊥AG,据此证明;
②过点C作CH⊥AG于H,设CG=x,GH=y,由角平分线的性质可得CH=CE,证明Rt△ACE≌Rt△ACH,推出EF∥AC,由平行线分线段成比例的性质可得BE,由弧、弦以及圆周角的关系可得∠CAE=∠ABC,证明△AEB∽△CEA,△GHC∽△GEA,然后由相似三角形的性质求解即可
一、单选题
1.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
2.已知⊙O的半径为6cm,圆心O到直线a的距离为6cm,则直线a与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
3.如图,已知四边形 内接于 , ,则 的度数是( )。
A. B. C. D.
4.同一平面内, 一个点到圆的最小距离为 , 最大距离为 , 则该圆的半径为 ( )
A. 或 B. 或
C. 或 D. 或
5.如图所示,⊙O的半径为5,点O到直线l的距离为7,P是直线l上的一个动点,PQ与⊙O相切于点Q.则PQ的最小值为( )
A. B. C.2 D.2
6.如图,的内切圆与分别相切于点D,E,F,若,则的度数是( )
A. B. C. D.
7.如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点,则AD的长是( )
A.1 B. C. D.2
8.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙O的直径为15,则AC长为( )
A.10 B.13 C.12 D.11
9.如图,点A的坐标为(﹣3,2),⊙A的半径为1,P为坐标轴上一动点,PQ切⊙A于点Q,在所有P点中,使得PQ长最小时,点P的坐标为( )
A.(0,2) B.(0,3) C.(﹣2,0) D.(﹣3,0)
10.如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB=BC;④BD=CD, 其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.若扇形的圆心角为60°,半径为2,则该扇形的弧长是 (结果保留)
12.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为 .
13.如图,点A,B,C在圆O上,OC⊥AB,垂足为D,若⊙O的半径是10cm,AB=12cm,则CD= cm.
14.如图,PA,PB分别切⊙O于点A,B,Q是优弧上一点,若∠P=40°,则∠Q的度数是 .
15.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若⊙O半径是4,∠B=22.5°,那么BC的长是 .
16.已知:如图, 是 的直径,弦 交 于E点, , , ,则 的长为 .
17.如图,直线交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是 .
18.如图,半径为 的 中, 为直径,弦 且过半径 的中点,点 为 上一动点, 于点 .当点 从点 出发顺时针运动到点 时,点 所经过的路径长为 .
三、解答题
19.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于点 D,BC于点E,连接ED.求证:ED=EC.
20.如图为桥洞的形状,其正视图是由 和矩形ABCD构成.O点为 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求 所在⊙O的半径DO.
21.将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,求图中阴影部分的面积.
22.如图, 是 的外接圆, 切 于点 , 与直径 的延长线相交于点 .
(Ⅰ)如图①,若 ,求 的大小;
(Ⅱ)如图②,当 , 时,求 的大小和 的半径.
23.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧的中点BD交AC于点E.
(1)若,求.
(2)求证:AD2=DE DB.
(3)若BC=5,CD=,求DE的长.
24.如图,BC是⊙O的直径,AD是⊙O的弦,AD交BC于点E,连接AB,CD,过点E作EF⊥AB,垂足为F,∠AEF=∠D.
(1)求证:AD⊥BC;
(2)点G在BC的延长线上,连接AG,∠DAG=2∠D.
①求证:AG与⊙O相切;
②当 ,CE=4时,直接写出CG的长.
答案解析部分
1.【答案】B
【解析】【解答】如图,取AB的中点O,分别连接OC、OB,则OC⊥AB,且
在Rt△OBC中,OB=5,由勾股定理得:
点P线段BC上,则,即
由对称性,当点P在线段AC上时,
∴当点P在弦AB上时,
∵
∴选项B符合题意
故答案为:B
【分析】先作辅助线,取AB的中点O,分别连接OC、OB,取AB的中点O,根据垂径定理得OC⊥AB,且,然后在Rt△OBC中由勾股定理得OC=4,再由垂线段最短可得答案。
2.【答案】B
【解析】【解答】解:设圆心O到直线a的距离为d,则d=6 cm
∵⊙O的半径为6 cm,
即半径=d=6 cm,
∴直线a与⊙O的位置关系是相切.
故答案为:B.
【分析】由⊙O的半径为6cm,圆心O到直线a的距离d=6cm,根据直线与圆的位置关系判定方法:当d>r时,直线与圆相离,当d<r时,直线与圆相交,当d=r时,直线与圆相切,即可判断.
3.【答案】B
【解析】【解答】解:∵四边形ABCD为圆内接四边形,
∴∠ADC=180°-∠ABC=180°-70°=110°.
故答案为:B.
【分析】利用圆内接四边形的对角互补的性质列式计算即可.
4.【答案】C
【解析】【解答】解:分为两种情况:
①当点P在圆内时,最近点的距离为6cm,最远点的距离为8cm,则直径是14cm,因而半径是7cm;
②当点P在圆外时,最近点的距离为6cm,最远点的距离为8cm,则直径是2cm,因而半径是1cm.
故答案为:C.
【分析】①当点P在圆内时,直径是14cm,据此可得半径;②当点P在圆外时,直径是2cm,据此可得半径.
5.【答案】C
【解析】【解答】解:∵PQ与⊙O相切于点Q,
∴OQ⊥PQ,
∴PQ2=OP2-OQ2=OP2-52=OP2-25,
∴当OP最小时,PQ有最小值,
∵点O到直线l的距离为7,
∴OP的最小值为7,
∴PQ的最小值=,
故答案为:C.
【分析】由切线的性质可得OQ⊥PQ,由勾股定理可得PQ2=OP2-OQ2=OP2-52=OP2-25,所以可得当OP最小时,PQ有最小值,由于OP的最小值为7,从而得解.
6.【答案】D
【解析】【解答】解:连接OD、OF,如图所示:
∵△ABC的内切圆与AB、BC、AC分别相切于点D,E,F,,
∴,
∴;
故答案为:D.
【分析】连接OD、OF,根据切线的性质可得∠ADO=∠AFO=90°,由同弧所对的圆心角等于圆周角的2倍可得∠DOF=2∠DEF=100°,然后根据四边形内角和为360°进行计算.
7.【答案】B
【解析】【解答】解:连接CD,过点C作CE⊥AB于点E,
在Rt△ABC中,
解之:BC=3,
∴
∵
∴3×4=5CE
解之:CE=.
∴
∴BD=2BE=
∴.
故答案为:B.
【分析】连接CD,过点C作CE⊥AB于点E,利用解直角三角形求出BC的长,利用勾股定理求出AB的长;再利用三角形的面积公式求出CE的长;然后利用勾股定理求出BE的长,根据BD=2BE可求出BD的长;然后根据AD=AB-BD,代入计算求出AD的长.
8.【答案】C
【解析】【解答】解:如图,连接AD,BD,
∵点D是弧AC的中点,DE⊥AB于点E,
∴,∠AED=∠DEB=90°,DF=2DE,
∴∠ADE=∠B,AC=DF,
∴△AED∽△DEB,
∴,
∴DE2=AE·BE=3×(15-3)=36,
∴DE=6,
∴DF=2DE=12,
∴AC=DF=12.
故答案为:C.
【分析】连接AD,BD,根据垂径定理和圆周角定理得出∠ADE=∠B,DF=2DE,再根据等弧所对的弦相等得出AC=DF,利用相似三角形的判定与性质得出DE=6,从而得出DF=12,即可得出AC=12.
9.【答案】D
【解析】【解答】解:连接AQ、PA,如图,
∵PQ切⊙A于点Q,
∴AQ⊥PQ,
∴∠AQP=90°,
∴PQ= ,
当AP的长度最小时,PQ的长度最小,
∵AP⊥x轴时,AP的长度最小,
∴AP⊥x轴时,PQ的长度最小,
∵A(﹣3,2),
∴此时P点坐标为(﹣3,0).
故答案为:D.
【分析】先求出PQ= ,再根据点A的坐标求解即可。
10.【答案】B
【解析】【解答】连接DO,∵BC是⊙O的直径,AD是⊙O的切线,切点为D,∴∠BDC=∠ADO=90°,∵DO=CO,∴∠C=∠CDO=30°,∴∠A=30°,∠DBC=60°,
∠ADB=30°,∴AD=DC,故①正确;∵∠A=30°,∠DBC=60°,∴∠ADB=30°,∴AB=BD,故②正确;∵∠C=30°,∠BDC=90°,∴BD=BC,∵AB=BD,
∴AB=BC,故③正确;无法得到BD=CD,故④错误.故选:B
【分析】利用圆周角定理结合切线的性质得出∠BDC=∠ADO=90°,进而得出∠A,∠ADB的度数即可得出答案,再利用直角三角形中30°所对的边等于斜边的一半进而得出AB=BC,判断即可.
11.【答案】
【解析】【解答】解:依题意,n=,r=2,
∴扇形的弧长=.
故答案为:.
【分析】利用弧长公式计算即可.
12.【答案】45°
【解析】【解答】解:连接OB、OC,
∵四边形ABCD是正方形,
∴∠BOC=90°,
∴∠BPC=.
故答案为:45°.
【分析】连接OB、OC,由正方形的性质可得∠BOC=90°,然后根据圆周角定理进行解答.
13.【答案】2
【解析】【解答】解:∵OC是⊙O的半径且OC⊥AB,垂足为D,
∴OA=OC=10cm,AD= AB= ×12=6cm,
∵在Rt△AOD中,OA=10cm,AD=6cm,
∴OD= cm,
∴CD=OC﹣OD=10﹣8=2cm.
故答案为2.
【分析】在直角三角形AOD中利用勾股定理求出OD的值,然后利用CD=OC﹣OD即可求解。
14.【答案】70°
【解析】【解答】解:连接OA、OB,
∵PA,PB分别切⊙O于点A,B,
∴∠OAP=∠OBP=90°,又∠P=40°,
∴∠AOB=360°-90°-90°-40°=140°,
∴∠Q=∠AOB=70°,
故答案为:70°.
【分析】连接OA、OB,先根据切线的性质和四边形的内角和求出∠AOB,再利用圆周角的性质可得∠Q=∠AOB=70°。
15.【答案】
【解析】【解答】解:连接,如图,
AC是⊙O的切线,
是等腰直角三角形,
故答案为:
【分析】连接OA,根据,可得是等腰直角三角形,即可得到,再利用线段的和差可得。
16.【答案】
【解析】【解答】解:如图所示,过点O作OF⊥CD于F,连接OD,
∴∠OFE=90°, ,
∵∠AEC=30°,
∴ ,
∵BE=1,AE=5,
∴AB=BE+AE=6,
∵AB是直径,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
故答案为: .
【分析】过点O作OF⊥CD于F,连接OD,根据,可得,在直角△DOF中求得DF的长即可求解。
17.【答案】
【解析】【解答】解:∵直线交x轴于点A,交y轴于点B,
∴令x=0,得y=-3,令y=0,得x=-4,
∴A(,0),B(0.-3),
∴OA=,OB=3,
∴AB=6,
设⊙P与直线AB相切于D,
连接PD,
如图示:
则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴
∴
∴
∴或,
∴P点坐标为:
故答案为:.
【分析】易得A(,0),B(0,-3),然后求出OA、OB、AB,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=1,证明△APD∽△ABO,由相似三角形的性质可得AP,进而求出OP,据此可得点P的坐标.
18.【答案】
【解析】【解答】
点 的路径是以 为半径, 中点为圆心的一段圆弧
如图,连接 ,设 于点 ,连接 的中点 和点 ,
的半径为 ,弦 且过半径 的中点, 为直径
,
,
故答案为: .
【分析】连接AC,AO,由AB⊥CD,利用垂径定理得到G为AB的中点,由中点的定义确定出OG的长,在直角三角形AOG中,由AO与OG的长,利用勾股定理求出AG的长,进而确定出AB的长,由CO+GO求出CG的长,在直角三角形AGC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半圆,如图所示。当E位于点B时,CG⊥AE,此时F、G重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发,顺时针运动到点D时,点F所经过的路径长弧AG,在直角三角形ACG中,利用锐角三角函数定义求出∠ACG的度数,进而确定出弧AG所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出弧AG的长,即可求出点F所经过的路径长。
19.【答案】解:∵AB=AC,
∴∠B=∠C,
∵四边形ABED是圆内接四边形,
∴∠CDE=∠B,
∴∠CDE=∠C,
∴CE=DE.
【解析】【分析】根据等腰三角形的性质和圆内接四边形的性质解答即可;
20.【答案】解:∵OE⊥弦CD于点F,CD为8米,EF为2米,
∴EO垂直平分CD,DF=4m,FO=DO﹣2,在Rt△DFO中,DO2=FO2+DF2,则DO2=(DO﹣2)2+42,解得:DO=5.
答:弧CD所在⊙O的半径DO为5m.
【解析】【分析】根据垂径定理得出EO垂直平分CD,DF=4m,然后利用勾股定理建立方程,求解即可得出OD的长。
21.【答案】解:∵∠BCA=90°,∠BAC=30°,AB=4,∴BC=2,∠CBC′=120°,∠A′BA=120°,
由旋转知△A′BC′≌△ABC ∴ S△A′BC′=S△ABC,
∴S阴影=S△A′BC′+S扇形ABA′-S扇形CBC′-S△ABC= S扇形ABA′-S扇形CBC′= ×(42-22)=4π(cm2).
【解析】【分析】根据图形阴影部分的面积转化为圆心角为 120° ,两个半径分别为4和2的圆环的面积,利用扇形得面积公式求解即可。
22.【答案】解:(Ⅰ)连接 .
∵ 切 于点 ,
∴ ,∴ ,
∵ ,
∴ ,
∴ .
(Ⅱ)连接 ,设 .
∵ ,∴ ,
∵ ,∴ ,
∴ .
∵ 是 的切线,
∴ ,即 ,
在 中, ,
即 ,
解得 ,
∴ .
在 中, ,
∵ ,
∴ ,
∵ ,
∴ ,即 的半径为2.
【解析】【分析】(1)先求出 , 再求出∠AOB=142°,最后求解即可;
(2)先求出 ,再求出 , 最后求解即可。
23.【答案】(1)解:∵BC是⊙O的直径
∴∠CAB=90°
∵
∴∠ABC=90°-30°=60°
∵D是劣弧的中点,得,
∴∠ABD=∠DAC=30°
∴=
(2)证明:由(1)得∠ABD=∠DAC,
又∵∠ADB=∠EDA,
∴△ABD∽△EAD,
∴AD2=DE DB;
(3)解:由D是劣弧的中点,得AD=DC,则DC2=DE DB
∵CB是直径,
∴△BCD是直角三角形.
∴BD=,由DC2=DE DB得,
()2=2DE,
解得:DE=.
【解析】【分析】(1)由圆周角定理可得∠CAB=90°,则∠ABC=90°-∠ACB=60°,根据中点的概念可得,由圆周角定理可得∠ABD=∠DAC=30°,据此求解;
(2)由(1)得∠ABD=∠DAC,证明△ABD∽△EAD,然后由相似三角形的性质证明即可;
(3)根据弧、弦的关系可得AD=DC,则DC2=DE DB,由勾股定理求出BD,然后根据DC2=DE DB就可求出DE.
24.【答案】(1)证明:∵EF⊥AB,
∴∠AFE=90°,
∴∠AEF+∠EAF=90°,
∵∠AEF=∠D,∠ABE=∠D,
∴∠ABE+∠EAF=90°,
∴∠AEB=90°,
∴AD⊥BC
(2)解:①证明:连接OA,AC.
∵AD⊥BC,
∴AE=ED,
∴CA=CD,
∴∠D=∠CAD,
∵∠GAE=2∠D,
∴∠CAG=∠CAD=∠D,
∵OC=OA,
∴∠OCA=∠OAC,
∵∠CEA=90°,
∴∠CAE+∠ACE=90°,
∴∠CAG+∠OAC=90°,
∴OA⊥AG,
∴AG是⊙O的切线.
②解:过点C作CH⊥AG于H.设CG=x,GH=y.
∵CA平分∠GAE,CH⊥AG,CE⊥AE,
∴CH=CE,
∵∠AEC=∠AHC=90°,AC=AC,EC=CH,
∴Rt△ACE≌Rt△ACH(HL),
∴AE=AH,
∵EF⊥AB,BC是直径,
∴∠BFE=∠BAC,
∴EF∥AC,
∴ ,
∵CE=4,
∴BE=10,
∵BC⊥AD,
∴ ,
∴∠CAE=∠ABC,
∵∠AEC=∠AEB=90°,
∴△AEB∽△CEA,
∴ ,
∴AE2=4×10,
∵AE>0,
∴AE= ,
∴AH=AE= ,
∵∠G=∠G,∠CHG=∠AEG=90°,
∴△GHC∽△GEA,
∴ ,
∴ ,
解得x= .
经检验:x= 是原方程的根且符合题意,
【解析】【分析】(1)由垂直的概念可得∠AFE=90°,由圆周角定理可得∠ABE=∠D,结合已知条件可推出∠AEB=90°,据此证明;
(2)①连接OA,AC,由垂径定理可得AE=ED,由等腰三角形的性质可得∠D=∠CAD,∠OCA=∠OAC,结合已知条件可得∠CAG=∠CAD=∠D,推出OA⊥AG,据此证明;
②过点C作CH⊥AG于H,设CG=x,GH=y,由角平分线的性质可得CH=CE,证明Rt△ACE≌Rt△ACH,推出EF∥AC,由平行线分线段成比例的性质可得BE,由弧、弦以及圆周角的关系可得∠CAE=∠ABC,证明△AEB∽△CEA,△GHC∽△GEA,然后由相似三角形的性质求解即可
