斜率等差模型课件-2022届高三数学二轮专题复习(18张ppt)
文档属性
| 名称 | 斜率等差模型课件-2022届高三数学二轮专题复习(18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 15:25:31 | ||
图片预览



文档简介
(共18张PPT)
斜率等差模型
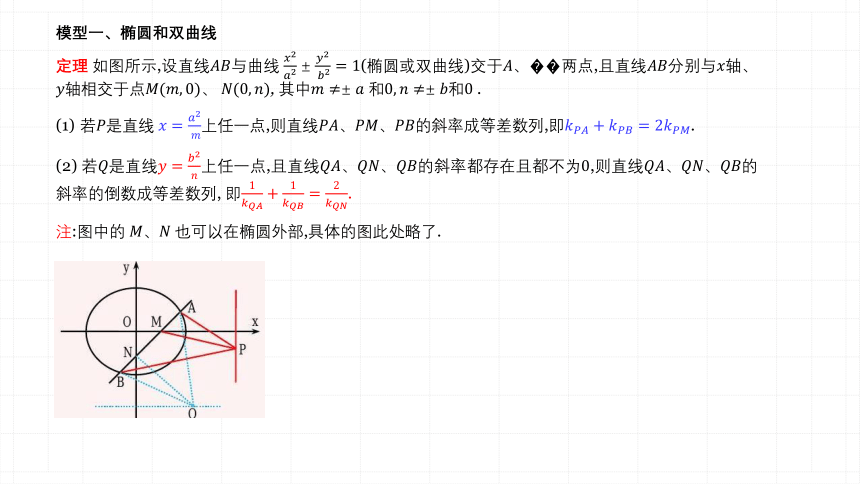
模型一、椭圆和双曲线
定理 如图所示,设直线与曲线 (椭圆或双曲线)交于两点,且直线分别与轴、轴相交于点, 其中 和和0 .
若是直线 上任一点,则直线的斜率成等差数列,即.
(2) 若是直线上任一点,且直线的斜率都存在且都不为0,则直线的斜率的倒数成等差数列, 即.
注:图中的 也可以在椭圆外部,具体的图此处略了.
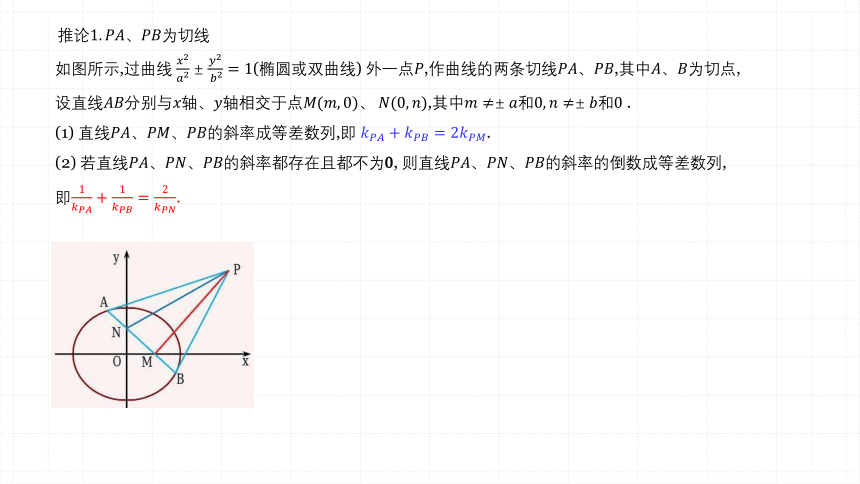
推论为切线
如图所示,过曲线 (椭圆或双曲线) 外一点,作曲线的两条切线,其中为切点,
设直线分别与轴、轴相交于点,其中和和0 .
(1) 直线的斜率成等差数列,即 .
(2) 若直线的斜率都存在且都不为0, 则直线的斜率的倒数成等差数列,
即.
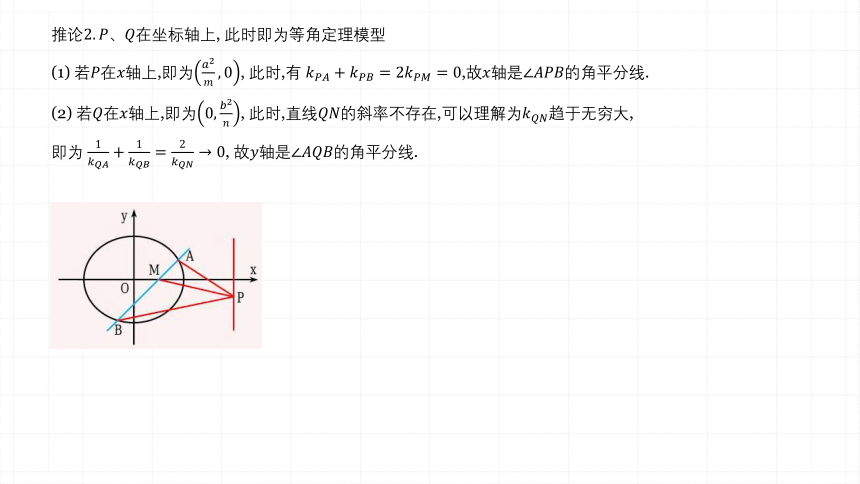
推论在坐标轴上, 此时即为等角定理模型
(1) 若在轴上,即为, 此时,有 ,故轴是的角平分线.
(2) 若在轴上,即为, 此时,直线的斜率不存在,可以理解为趋于无穷大,
即为 , 故轴是的角平分线.
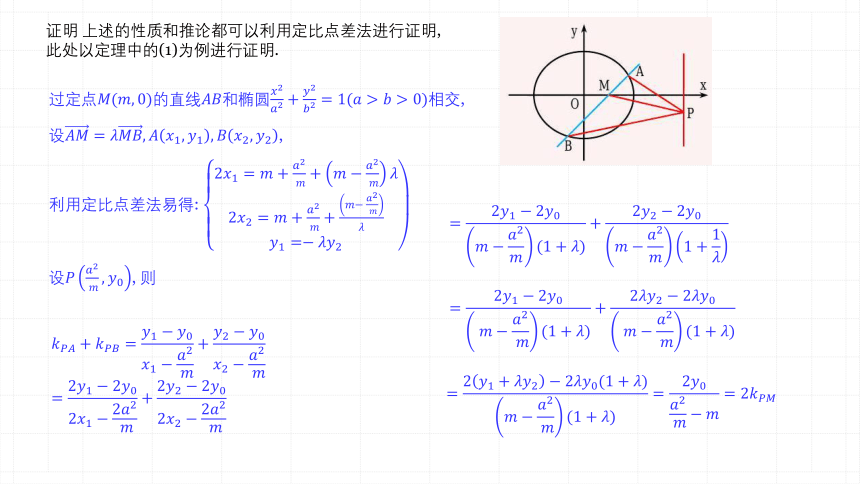
证明 上述的性质和推论都可以利用定比点差法进行证明,
此处以定理中的(1)为例进行证明.
过定点的直线和椭圆相交,
设,
利用定比点差法易得:
设, 则
例 已知椭圆的离心率为,以为圆心,椭圆的短半轴长为半径的圆与直线相切.
(1) 求椭圆C的标准方程;
(2) 已知点,和平面内一点,过点任作直线与椭圆相交于两点,设直线AN、NP、BN的斜率分别为,试求满足的关系式.
略解 (1)
(2) 设 ,
利用定比点差法:
故
因此,
即 .
背景
练习 过椭圆外一点 且 向椭圆作切线, 切点分别为,
直线交轴于点, 记直线斜率分别为.
(1) 当点的坐标为 时, 求直线的方程;
(2) 当时, 是否存在常数, 使得恒成立 若存在, 求的值; 若不存在, 说明理由.
答案 (1) ; (2) 存在, .
椭圆 的离心率.
(1) 求椭圆的方程;
(2) 如图, 是椭圆的顶点, 是椭圆上除顶点外的任意点, 直线交轴于点直线交于点, 设的斜率为的斜率为, 证明: 为定值.
(1)
抛物线
定理 (1) 如图,设直线与抛物线交于两点,且直线与轴相交于点,
若是直线x上任一点,则直线的斜率成等差数列,即.
(2) 如图,设直线与抛物线交于两点,且直线与轴相交于点,
若是直线上任一点,若直线的斜率都存在,
则直线的斜率的倒数成等差数列,即.
注 (1)图中的 也可以在抛物线外部,具体的图此处略了.
(2)定理和推论1的图合在一起画了,通过对比,可知清楚的发现,推论1就是定理的特例.
推论为切线
(1) 如图,过抛物线 外一点,作抛物线的两条切线, 其中为切点,设直线与轴交于点 , 则直线的斜率成等差数列, 即.
(2) 如图,过抛物线外一点,作抛物线的两条切线,其中为切点,设直线与轴交于点 ,则直线的斜率成等差数列,即.
推论 在坐标轴上, 此时即为等角定理模型
(1) 若在 轴上,即为, 此时,有, 故轴是的角平分线.
(2)若在轴上,即为,此时,直线的斜率不存在,可以理解为趋于无穷大,即为,
故轴是的角平分线.
证法一 上述的性质和推论都可以利用定比点差法进行证明,
此处以定理中的(1)为例进行证明.
设 ,
利用定比点差法易得:
设 ,
故
证法二 设
则直线 的方程为:
代入点 得:
故
注 相比较而言,显然利用定比点差法证明更加简单! 但是,从应试的角度个人建议,对于抛物线,除非牵扯到定比,一般不使用定比点差法,而是优先使用抛物线的两点式方程!
例 已知抛物线 的焦点恰好在圆 上.
(1) 求抛物线的标准方程;
(2) 过点作直线交抛物线于两点,则在直线上是否存在定点, 使直线的斜率是直线 斜率的等差中项 若存在, 求出点的坐标; 若不存在, 请说明理由.
解 (1) ;
(2)设
则直线的方程为:
代入点 得:
假设存在定点, 使得
即, 整理得:
欲使得该式对任意 恒成立,
则必有
解得
故存在点
模型二
定理 过圆锥曲线 (椭圆、双曲线、拋物线) 焦点的任一直线交圆锥曲线于两点, 交对应准线于点, 点是过焦点, 且垂直长轴 (抛物线为对称轴) 的直线上异于的任意一点, 则直线 、 的斜率成等差数列,
推广 显然, 焦点和准线是一对极点极线, 因此, 也可以推广到更一般的极点极线模型.
下面以椭圆为例, 对一般情况进行简单的证明.
例 如图所示,过点且不和轴垂直的直线和椭圆 交于两点,
同时交直线 于点,设为直线上异于点的任一点,求证:.
分析 注意到点和直线恰好是一对极点极线,
因此, 是一组调和点列,
则有 ,
因此, 可以尝试利用定比点差法进行证明,
下面给出严格的证明.
证明 设
设
则 (1)
对 “ ” 利用定比点差法: (先不计算)
和(1)中的 “ ” 类比
可得 , 故
同时, 继续计算解得:
由于
只需要将 “ ” 的形式向 “ ” 的形式变形靠拢即可.
因此,
注 上述证明稍微复杂了点, 实际上, 利用常规方法, 设直线 为 , 然后联立方程, 利用韦达定理进行证明更加简单
例 已知抛物线 的焦点为 , 其准线方程为 , 设不过点 的直线 与抛物线 交于不同的两点 ( 不关于 轴对称), 若 三条直线的斜率依次成等差数列.
(1) 求线段 的中点的横坐标; (2) 求直线 的斜率的取值范围.
答案 (1) , 横坐标为 1 ; (2) .
斜率等差模型
模型一、椭圆和双曲线
定理 如图所示,设直线与曲线 (椭圆或双曲线)交于两点,且直线分别与轴、轴相交于点, 其中 和和0 .
若是直线 上任一点,则直线的斜率成等差数列,即.
(2) 若是直线上任一点,且直线的斜率都存在且都不为0,则直线的斜率的倒数成等差数列, 即.
注:图中的 也可以在椭圆外部,具体的图此处略了.
推论为切线
如图所示,过曲线 (椭圆或双曲线) 外一点,作曲线的两条切线,其中为切点,
设直线分别与轴、轴相交于点,其中和和0 .
(1) 直线的斜率成等差数列,即 .
(2) 若直线的斜率都存在且都不为0, 则直线的斜率的倒数成等差数列,
即.
推论在坐标轴上, 此时即为等角定理模型
(1) 若在轴上,即为, 此时,有 ,故轴是的角平分线.
(2) 若在轴上,即为, 此时,直线的斜率不存在,可以理解为趋于无穷大,
即为 , 故轴是的角平分线.
证明 上述的性质和推论都可以利用定比点差法进行证明,
此处以定理中的(1)为例进行证明.
过定点的直线和椭圆相交,
设,
利用定比点差法易得:
设, 则
例 已知椭圆的离心率为,以为圆心,椭圆的短半轴长为半径的圆与直线相切.
(1) 求椭圆C的标准方程;
(2) 已知点,和平面内一点,过点任作直线与椭圆相交于两点,设直线AN、NP、BN的斜率分别为,试求满足的关系式.
略解 (1)
(2) 设 ,
利用定比点差法:
故
因此,
即 .
背景
练习 过椭圆外一点 且 向椭圆作切线, 切点分别为,
直线交轴于点, 记直线斜率分别为.
(1) 当点的坐标为 时, 求直线的方程;
(2) 当时, 是否存在常数, 使得恒成立 若存在, 求的值; 若不存在, 说明理由.
答案 (1) ; (2) 存在, .
椭圆 的离心率.
(1) 求椭圆的方程;
(2) 如图, 是椭圆的顶点, 是椭圆上除顶点外的任意点, 直线交轴于点直线交于点, 设的斜率为的斜率为, 证明: 为定值.
(1)
抛物线
定理 (1) 如图,设直线与抛物线交于两点,且直线与轴相交于点,
若是直线x上任一点,则直线的斜率成等差数列,即.
(2) 如图,设直线与抛物线交于两点,且直线与轴相交于点,
若是直线上任一点,若直线的斜率都存在,
则直线的斜率的倒数成等差数列,即.
注 (1)图中的 也可以在抛物线外部,具体的图此处略了.
(2)定理和推论1的图合在一起画了,通过对比,可知清楚的发现,推论1就是定理的特例.
推论为切线
(1) 如图,过抛物线 外一点,作抛物线的两条切线, 其中为切点,设直线与轴交于点 , 则直线的斜率成等差数列, 即.
(2) 如图,过抛物线外一点,作抛物线的两条切线,其中为切点,设直线与轴交于点 ,则直线的斜率成等差数列,即.
推论 在坐标轴上, 此时即为等角定理模型
(1) 若在 轴上,即为, 此时,有, 故轴是的角平分线.
(2)若在轴上,即为,此时,直线的斜率不存在,可以理解为趋于无穷大,即为,
故轴是的角平分线.
证法一 上述的性质和推论都可以利用定比点差法进行证明,
此处以定理中的(1)为例进行证明.
设 ,
利用定比点差法易得:
设 ,
故
证法二 设
则直线 的方程为:
代入点 得:
故
注 相比较而言,显然利用定比点差法证明更加简单! 但是,从应试的角度个人建议,对于抛物线,除非牵扯到定比,一般不使用定比点差法,而是优先使用抛物线的两点式方程!
例 已知抛物线 的焦点恰好在圆 上.
(1) 求抛物线的标准方程;
(2) 过点作直线交抛物线于两点,则在直线上是否存在定点, 使直线的斜率是直线 斜率的等差中项 若存在, 求出点的坐标; 若不存在, 请说明理由.
解 (1) ;
(2)设
则直线的方程为:
代入点 得:
假设存在定点, 使得
即, 整理得:
欲使得该式对任意 恒成立,
则必有
解得
故存在点
模型二
定理 过圆锥曲线 (椭圆、双曲线、拋物线) 焦点的任一直线交圆锥曲线于两点, 交对应准线于点, 点是过焦点, 且垂直长轴 (抛物线为对称轴) 的直线上异于的任意一点, 则直线 、 的斜率成等差数列,
推广 显然, 焦点和准线是一对极点极线, 因此, 也可以推广到更一般的极点极线模型.
下面以椭圆为例, 对一般情况进行简单的证明.
例 如图所示,过点且不和轴垂直的直线和椭圆 交于两点,
同时交直线 于点,设为直线上异于点的任一点,求证:.
分析 注意到点和直线恰好是一对极点极线,
因此, 是一组调和点列,
则有 ,
因此, 可以尝试利用定比点差法进行证明,
下面给出严格的证明.
证明 设
设
则 (1)
对 “ ” 利用定比点差法: (先不计算)
和(1)中的 “ ” 类比
可得 , 故
同时, 继续计算解得:
由于
只需要将 “ ” 的形式向 “ ” 的形式变形靠拢即可.
因此,
注 上述证明稍微复杂了点, 实际上, 利用常规方法, 设直线 为 , 然后联立方程, 利用韦达定理进行证明更加简单
例 已知抛物线 的焦点为 , 其准线方程为 , 设不过点 的直线 与抛物线 交于不同的两点 ( 不关于 轴对称), 若 三条直线的斜率依次成等差数列.
(1) 求线段 的中点的横坐标; (2) 求直线 的斜率的取值范围.
答案 (1) , 横坐标为 1 ; (2) .
同课章节目录
