2022届高考数学冲刺课第3讲中点弦模型课件(34张PPT)
文档属性
| 名称 | 2022届高考数学冲刺课第3讲中点弦模型课件(34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 08:37:34 | ||
图片预览










文档简介
(共34张PPT)
高考数学冲刺(3)
中点弦模型
主讲人: |
01椭圆焦点三角形中的秒杀结论02椭圆焦点、通径、渐近线秒杀技巧03椭圆中点弦模型04函数奇偶性、单调性、周期性秒杀技巧05综合线性规划、二项式、不等式秒杀06数列列举法秒杀数列07数列数列四大求和方法08综合排列组合七大解题策略09函数函数值域技巧、数形结合技巧10综合巧解高考小题2个定理推广:圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)圆周角定理的推广:若AB为“有心圆锥曲线”的直径,点M为曲线上异于A,B的任意一点,则kMA·kMB=e2-1.(可用点差法证明记住结论即可)秒杀类型1秒杀类型2秒杀类型3口算秒杀公式标准书写模板中点弦模型求曲线方程:秒杀结论①圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)秒杀类型1ABM例题1.秒杀类型1秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.FMAB例题1.点拨:直接利用秒杀结论①即可快速求出.kAB=kOM=kAB·kOM=e2-1且c=3可求出,故选:D秒杀类型1秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.FMAB练习1.秒杀类型1秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.练习1.点拨:直接利用秒杀结论①即可快速求出.kAB=kON=kAB·kOM=e2-1且c=3可求出,故选:B秒杀类型1秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.中点弦模型求直线斜率:秒杀结论①圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)秒杀结论②圆周角定理的推广:若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.(可用点差法证明记住结论即可)ABMABP秒杀类型2中点弦模型求直线斜率:秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;直线l与抛物线于A,B,M为AB的中点,则=,·=p.秒杀类型2例题1.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型2PA1A2例题1.点拨:直接利用秒杀结论②即可快速求出., e=由·=e2-1有故选:B.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型2PA1A2例题3.已知抛物线的焦点为F,△ABC的顶点都在抛物线上,且满足,则.秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;O是三角形ABC的重心(重心是三条中线的交点)秒杀类型2例题3.已知抛物线的焦点为F,△ABC的顶点都在抛物线上,且满足,则.分析:说明F是△ABC的重心,所以三个中点纵坐标的和为0,三个中点构成的三角形与原三角形同重心,故纵坐标之和也为0,记为0由秒杀结论③kAB·=p所以++=答案:0秒杀类型2秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;O是三角形ABC的重心(重心是三条中线的交点)练习1.秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.秒杀类型2练习1.点拨:直接利用秒杀结论①即可快速求出.中点M, e=由kAB·kOM=e2-1kAB-1答案:2x+2y-3=0.秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.秒杀类型2练习2.(西安区校级月考)已知椭圆r:(a>b>0)的右焦点为F(1,0),且离心率为,三角形ABC的三个顶点都在椭圆r上,设它的三条边AB、BC、AC的中点分别为D、E、M,且三条边所在直线的斜率分别为k1、k2、k3,且k1、k2、k3均不为0.O为坐标原点,若直线OD、OE、OM的斜率之和为1.则+( )A.B.-3 C.D.秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.秒杀类型2FCABDEMO练习2.(西安区校级月考)已知椭圆r:(a>b>0)的右焦点为F(1,0),且离心率为,三角形ABC的三个顶点都在椭圆r上,设它的三条边AB、BC、AC的中点分别为D、E、M,且三条边所在直线的斜率分别为k1、k2、k3,且k1、k2、k3均不为0.O为坐标原点,若直线OD、OE、OM的斜率之和为1.则+( )A.B.-3 C.D.点拨:直接利用秒杀结论①即可快速求出.k1·kOD=e2-1=得=kOD同理=kOE,kOM+(kOD+kOE+kOM)=故选:A.秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.秒杀类型2FCABDEMO练习3.(浙江卷)已知抛物线上永远有关于直线l:y=4x+m对称的相异两点,则实数m的取值范围是.秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;秒杀类型2练习解析:设抛物线上A、B两点关于直线l对称,且弦AB的中点为P(x0,y0)根据题意,点P在直线l上,AB⊥l,∴kAB=.又,,∴p=6.由秒杀结论③ kAB·=p得=6,∴=24又由=4得.点P(x0,y0)在抛物线的开口内,∴.解得:m<216故实数m的取值范围(,216).答案:(,216).秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;秒杀类型2中点弦模型求离心率:秒杀结论①圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)秒杀结论②圆周角定理的推广:若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.(可用点差法证明记住结论即可)秒杀结论④秒杀类型3例题1.(肇庆二模)已知椭圆C(a>b>0)的左右顶点分别为A,B,P是椭圆上异于A,B的一点,若直线PA的斜率kPA与直线PB的斜率kPB乘积kPA·kPB=,则椭圆C的离心率为( )A.B.C.D.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3PAB例题1.(肇庆二模)已知椭圆C:(a>b>0)的左右顶点分别为A,B,P是椭圆上异于A,B的一点,若直线PA的斜率kPA与直线PB的斜率kPB乘积kPA·kPB=,则椭圆C的离心率为( )A.B.C.D.点拨:直接利用秒杀结论②即可快速求出.kPA·kPB==e2-1=故选:D.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3PAB例题2.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3例题2.点拨:直接利用秒杀结论②即可快速求出.kMA=tan30°=,kMB=tan60°=kMA·kMB=e2-1=1=故选:D.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3例题3.秒杀结论④秒杀类型3例题3.解析:取AB的中点M,连接PM,因为|PA|=|PB|,所以PM⊥AB,又kAB=故kPM=-3联立,所以kOM=由秒杀结论③有kAB·kOM=e2-1=答案:.秒杀结论④秒杀类型3练习1. (嘉峪关校级月考)已知平行四边形ABCD内接于椭圆C:(a>b>0),且AB,AD斜率之积的范围为(,),则椭圆C离心率的取值范围是( )A.() B.() C. () D.()秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3练习1. (嘉峪关校级月考)已知平行四边形ABCD内接于椭圆C:(a>b>0),且AB,AD斜率之积的范围为(,),则椭圆C离心率的取值范围是( )A.() B.() C. () D.()点拨:直接利用秒杀结论②即可快速求出.e2-1=kAB·kAD(,),e故选:A.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3圆锥曲线中的口算秒杀公式:口算秒杀公式圆锥曲线中的口算秒杀公式:口算秒杀公式圆锥曲线解答题标准书写模板:标准书写模板圆锥曲线解答题标准书写模板:4.圆锥曲线计算量大的题目的书写方式差不多,以上是最基本的书写步骤,根据题目中条件的具体情况,可以适当的删减或调整局部的书写。标准书写模板秒杀结论①
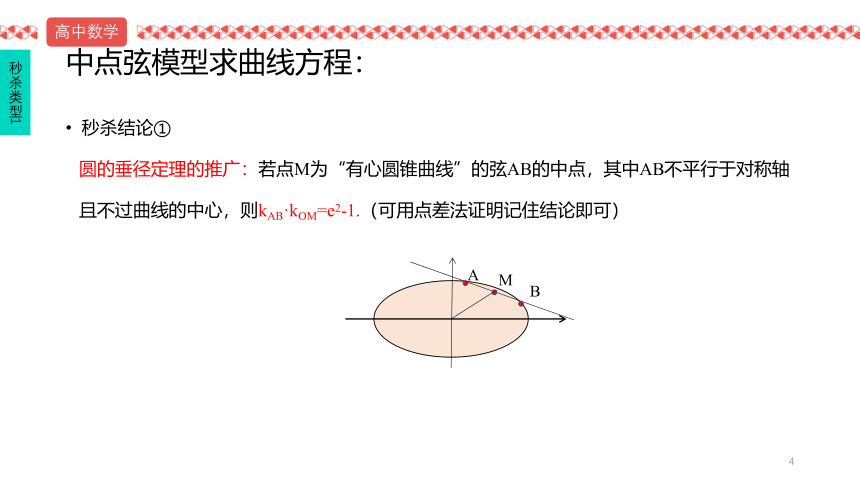
圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于
对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)
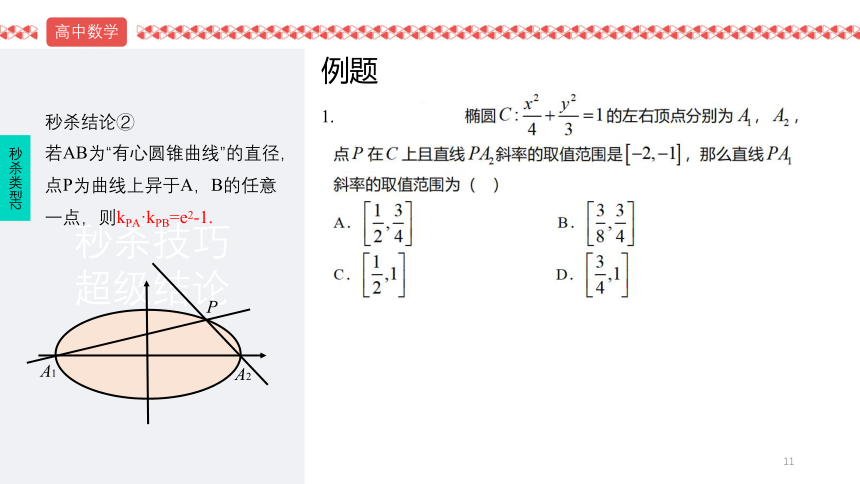
秒杀结论②
圆周角定理的推广:若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任
意一点,则kPA·kPB=e2-1.(可用点差法证明记住结论即可)
秒杀结论③
直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=, kAB· =p;
直线l与抛物线于A,B,M为AB的中点,则=, · =p.
秒杀结论④
当堂总结
高考数学冲刺(3)
中点弦模型
主讲人: |
01椭圆焦点三角形中的秒杀结论02椭圆焦点、通径、渐近线秒杀技巧03椭圆中点弦模型04函数奇偶性、单调性、周期性秒杀技巧05综合线性规划、二项式、不等式秒杀06数列列举法秒杀数列07数列数列四大求和方法08综合排列组合七大解题策略09函数函数值域技巧、数形结合技巧10综合巧解高考小题2个定理推广:圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)圆周角定理的推广:若AB为“有心圆锥曲线”的直径,点M为曲线上异于A,B的任意一点,则kMA·kMB=e2-1.(可用点差法证明记住结论即可)秒杀类型1秒杀类型2秒杀类型3口算秒杀公式标准书写模板中点弦模型求曲线方程:秒杀结论①圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)秒杀类型1ABM例题1.秒杀类型1秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.FMAB例题1.点拨:直接利用秒杀结论①即可快速求出.kAB=kOM=kAB·kOM=e2-1且c=3可求出,故选:D秒杀类型1秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.FMAB练习1.秒杀类型1秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.练习1.点拨:直接利用秒杀结论①即可快速求出.kAB=kON=kAB·kOM=e2-1且c=3可求出,故选:B秒杀类型1秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.中点弦模型求直线斜率:秒杀结论①圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)秒杀结论②圆周角定理的推广:若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.(可用点差法证明记住结论即可)ABMABP秒杀类型2中点弦模型求直线斜率:秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;直线l与抛物线于A,B,M为AB的中点,则=,·=p.秒杀类型2例题1.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型2PA1A2例题1.点拨:直接利用秒杀结论②即可快速求出., e=由·=e2-1有故选:B.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型2PA1A2例题3.已知抛物线的焦点为F,△ABC的顶点都在抛物线上,且满足,则.秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;O是三角形ABC的重心(重心是三条中线的交点)秒杀类型2例题3.已知抛物线的焦点为F,△ABC的顶点都在抛物线上,且满足,则.分析:说明F是△ABC的重心,所以三个中点纵坐标的和为0,三个中点构成的三角形与原三角形同重心,故纵坐标之和也为0,记为0由秒杀结论③kAB·=p所以++=答案:0秒杀类型2秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;O是三角形ABC的重心(重心是三条中线的交点)练习1.秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.秒杀类型2练习1.点拨:直接利用秒杀结论①即可快速求出.中点M, e=由kAB·kOM=e2-1kAB-1答案:2x+2y-3=0.秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.秒杀类型2练习2.(西安区校级月考)已知椭圆r:(a>b>0)的右焦点为F(1,0),且离心率为,三角形ABC的三个顶点都在椭圆r上,设它的三条边AB、BC、AC的中点分别为D、E、M,且三条边所在直线的斜率分别为k1、k2、k3,且k1、k2、k3均不为0.O为坐标原点,若直线OD、OE、OM的斜率之和为1.则+( )A.B.-3 C.D.秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.秒杀类型2FCABDEMO练习2.(西安区校级月考)已知椭圆r:(a>b>0)的右焦点为F(1,0),且离心率为,三角形ABC的三个顶点都在椭圆r上,设它的三条边AB、BC、AC的中点分别为D、E、M,且三条边所在直线的斜率分别为k1、k2、k3,且k1、k2、k3均不为0.O为坐标原点,若直线OD、OE、OM的斜率之和为1.则+( )A.B.-3 C.D.点拨:直接利用秒杀结论①即可快速求出.k1·kOD=e2-1=得=kOD同理=kOE,kOM+(kOD+kOE+kOM)=故选:A.秒杀结论①若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.秒杀类型2FCABDEMO练习3.(浙江卷)已知抛物线上永远有关于直线l:y=4x+m对称的相异两点,则实数m的取值范围是.秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;秒杀类型2练习解析:设抛物线上A、B两点关于直线l对称,且弦AB的中点为P(x0,y0)根据题意,点P在直线l上,AB⊥l,∴kAB=.又,,∴p=6.由秒杀结论③ kAB·=p得=6,∴=24又由=4得.点P(x0,y0)在抛物线的开口内,∴.解得:m<216故实数m的取值范围(,216).答案:(,216).秒杀结论③直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=,kAB·=p;秒杀类型2中点弦模型求离心率:秒杀结论①圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)秒杀结论②圆周角定理的推广:若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.(可用点差法证明记住结论即可)秒杀结论④秒杀类型3例题1.(肇庆二模)已知椭圆C(a>b>0)的左右顶点分别为A,B,P是椭圆上异于A,B的一点,若直线PA的斜率kPA与直线PB的斜率kPB乘积kPA·kPB=,则椭圆C的离心率为( )A.B.C.D.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3PAB例题1.(肇庆二模)已知椭圆C:(a>b>0)的左右顶点分别为A,B,P是椭圆上异于A,B的一点,若直线PA的斜率kPA与直线PB的斜率kPB乘积kPA·kPB=,则椭圆C的离心率为( )A.B.C.D.点拨:直接利用秒杀结论②即可快速求出.kPA·kPB==e2-1=故选:D.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3PAB例题2.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3例题2.点拨:直接利用秒杀结论②即可快速求出.kMA=tan30°=,kMB=tan60°=kMA·kMB=e2-1=1=故选:D.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3例题3.秒杀结论④秒杀类型3例题3.解析:取AB的中点M,连接PM,因为|PA|=|PB|,所以PM⊥AB,又kAB=故kPM=-3联立,所以kOM=由秒杀结论③有kAB·kOM=e2-1=答案:.秒杀结论④秒杀类型3练习1. (嘉峪关校级月考)已知平行四边形ABCD内接于椭圆C:(a>b>0),且AB,AD斜率之积的范围为(,),则椭圆C离心率的取值范围是( )A.() B.() C. () D.()秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3练习1. (嘉峪关校级月考)已知平行四边形ABCD内接于椭圆C:(a>b>0),且AB,AD斜率之积的范围为(,),则椭圆C离心率的取值范围是( )A.() B.() C. () D.()点拨:直接利用秒杀结论②即可快速求出.e2-1=kAB·kAD(,),e故选:A.秒杀结论②若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任意一点,则kPA·kPB=e2-1.秒杀类型3圆锥曲线中的口算秒杀公式:口算秒杀公式圆锥曲线中的口算秒杀公式:口算秒杀公式圆锥曲线解答题标准书写模板:标准书写模板圆锥曲线解答题标准书写模板:4.圆锥曲线计算量大的题目的书写方式差不多,以上是最基本的书写步骤,根据题目中条件的具体情况,可以适当的删减或调整局部的书写。标准书写模板秒杀结论①
圆的垂径定理的推广:若点M为“有心圆锥曲线”的弦AB的中点,其中AB不平行于
对称轴且不过曲线的中心,则kAB·kOM=e2-1.(可用点差法证明记住结论即可)
秒杀结论②
圆周角定理的推广:若AB为“有心圆锥曲线”的直径,点P为曲线上异于A,B的任
意一点,则kPA·kPB=e2-1.(可用点差法证明记住结论即可)
秒杀结论③
直线l与抛物线于A,B,M为AB的中点,则kAB·kOM=, kAB· =p;
直线l与抛物线于A,B,M为AB的中点,则=, · =p.
秒杀结论④
当堂总结
同课章节目录
