2022届高考数学二轮专题超几何分布与二项分布课件(35张PPT)
文档属性
| 名称 | 2022届高考数学二轮专题超几何分布与二项分布课件(35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 08:41:54 | ||
图片预览











文档简介
(共35张PPT)
内 容 内容 要求 离散型随机变量的分布列 有限个值的离散型随机变量的分布列的概念、性质 理解
超几何分布的概念、导出过程及其应用 理解
条件概率及事件间相互独立的概念 了解
n次独立重复实验模型、 二项分布及其应用 理解
离散型随机变量分布列的数学期望、方差及其计算 理解
正态分布 正态分布曲线的特点及其意义 了解
一.考纲解读
超几何分布
一般地,设有总数为件的两类物品,其中类有件,
从所有物品中任取件(),这件中所含类物品件数是一个离散型随机变量,
它取值为时的概率为
称上面的分布列为超几何分布列.
如果随机变量的分布列为超几何分布列,则称随机变量服从超几何分布.
(,为和中较小的一个).
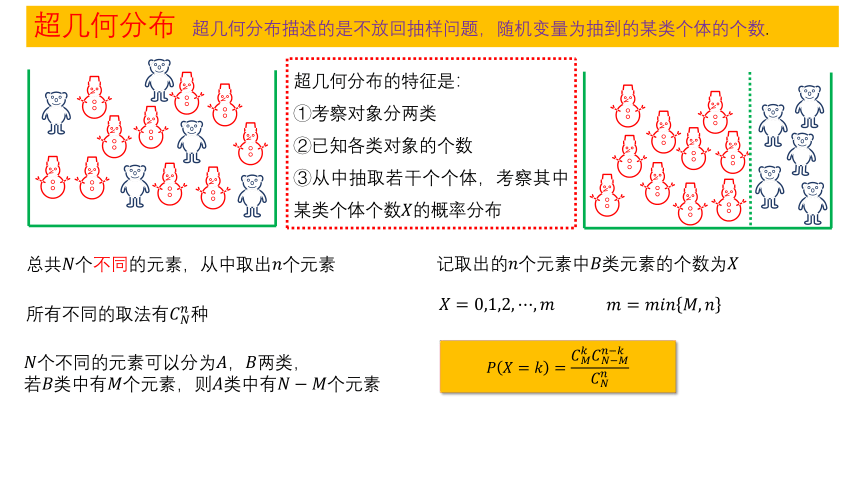
超几何分布 超几何分布描述的是不放回抽样问题,随机变量为抽到的某类个体的个数.
总共个不同的元素,从中取出个元素
所有不同的取法有种
个不同的元素可以分为,两类,
若类中有个元素,则类中有个元素
记取出的个元素中类元素的个数为
超几何分布的特征是:
①考察对象分两类
②已知各类对象的个数
③从中抽取若干个个体,考察其中某类个体个数的概率分布
独立重复试验与二项分布:
一般地,如果在一次试验中事件发生的概率是,那么在次独立重复试验中,事件恰好发生次的概率为
此时我们称随机变量服从二项分布,记作:
… …
于是得到随机变量的概率分布如下:()
在次独立重复试验中这个事件发生的次数是一个随机变量;
判断随机试验是否服从二项分布的依据
1,在每一次试验中,事件发生的概率相同
2,各次试验中的事件是相互独立的
3,在每一次试验中,试验的结果只有两个,即发生,不发生
※离散型随机变量的方差
若随机变量服从参数为和的二项分布,则
()
,
【典例】一出租车司机从某饭店到火车站途中有6个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率是
(1)求这位司机遇到红灯数ξ的期望与方差.
(2)若遇上红灯,则需等待30秒,求司机总共等待时间η的期望与方差.
(1)易知司机遇上红灯次数ξ
所以,(ξ)==
(2)由已知=,所以,
.
※例题分析
为实数,则
某批件产品的次品率为,现从中任意的依次抽取件进行检验,问:
(1)当时,分别以放回和不放回的方式抽取,
恰好抽到件次品的概率是多少?
(2)根据(1)你对超几何分布与二项分布的关系有何认识?
回归教材,突破重点
【选修2-3P59B组第3题】
(1)在有放回的方式抽取中,每次抽取都是从这件产品中抽取, 从而抽到次品的概率都为0.02,可以把3次抽取看成是3次独立重复试验,这样抽到的次品数
恰好抽到1件次品的概率为
在无放回的方式抽取中,抽到的次品数X是随机变量,服从超几何分布,的分布与产品的总数有关,所以需要分三种情况分别计算:
1.当的时候,产品的总数为件,其中次品的件数为,合格品的件数为.从件产品中抽出件,其中恰好抽到件次品的概率为
3.当n=50000的时候,产品的总数为50000件,其中次品的件数为,合格品的件数为49000.从5000件产品中抽出3件,其中恰好抽到1件次品的概率为
2.当n=5000的时候,产品的总数为5000件,其中次品的件数为,合格品的件数为4900.从5000件产品中抽出3件,其中恰好抽到1件次品的概率为
(1)在有放回的方式抽取中
在无放回的方式抽取中
2.当n=5000
3.当n=50000
1.当n=500
(2)根据(1)的计算结果可以看出,当产品的总数很大时,超几何分布近似为二项分布而且随着总数的增加,这种近似的精度也在增加。
超几何分布与二项分布的联系与区别是什么?
在一个口袋中装有个红球、个白球,这些球除颜色外完全相同,一次从中摸出个球,摸到4个红球1个白球就是一等奖,求获一等奖的概率.
超几何分布
二项分布
超几何分布
二项分布
从概率分布表中发现,两种分布对应的概率相差不大
超几何分布与二项分布的联系与区别是什么?
超几何分布
二项分布
超几何分布
二项分布
现将问题数据改为个红球、个白球,其他条件不变
这时发现两种不同的分布其对应的概率之间的差距进一步缩小了,我们猜想:样本个数越大超几何分布和二项分布的对应概率相差就越小,当样本个数为无穷大时,超几何分布和二项分布的对应概率就相等,换而言之,超几何分布的极限就是二项分布.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的质量(单位:克),质量的分组区间为,, ,由此得到样本的频率分布直方图(如下图).
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设为质量超过505克的产品数量,求的分布列
(3)从该流水线上任取件产品,设为质量超过505克的产品数量,求的分布列.
经典例题
(答案:12件)
(2)重量超过505的产品数量为12件,则重量未超过505克的产品数量为28件,的取值为0,1,2,服从超几何分布,
(3)根据样本估计总体的思想,取一件产品,该产品的质量超过克的概率为 .
从流水线上任取件产品互不影响,该问题可看成2次独立重复试验,质量超过克的件数的可能取值为,,,且 即
期望为:
某调查机构对某校学生做了一个是否同意父母生“二孩”的抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是否同意父母生“二孩”,现已得知100人中同意父母生“二孩”的占,统计情况如下表:
同意 不同意 合计
男生 50
女生 40
合计 100
(1)求的值,根据以上数据,能否有的把握认为是否同意父母生“二孩”与性别有关?请说明理由;
(2)将上述调查所得的频率视为概率,现在从所有学生中,采取随机抽样的方法抽取位学生进行长期跟踪调查,记被抽取的4位学生中持“同意”态度的人数为,求的分布列及数学期望.
其中
解:(2) ,4
所以分布列为
数学期望为
3 4
(2)由题意知,持“同意”态度的学生占,即从学生中任意抽取到一名持“同意”态度的学生的概率是.
由于总体容量很大,故服从二项分布,即 从而
数学期望为
3 4
超几何分布 二项分布
区 别 超几何分布是不放回抽样问题,各次抽取不独立.随机变量为抽到某类个体的个数,超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型 二项分布的抽取是独立的,各次抽取相互独立.次独立重复试验中事件恰好发生次的概率可看作个互斥事件的和,其中每一个事件都可以看作个事件与个事件同时发生,只是发生的次序不同,其发生的概率都是
特 征 ①考查对象分两类 ②已知各类对象的个数 ③从中抽取若干个个体,考察某类个体数的概率分布 ①在每一次试验中某事件发生的概率是一个常数
②次试验不仅是在完全相同的情况下进行的重复试验,而且各次试验的结果是相互独立的;
=
联系 ,期望是相同的. 二项分布与超几何分布区别与联系
(2017年全国Ⅱ卷理科第13题)一批产品的二等品率为,从这批产品中每次随机取一件,有放回地抽取次.表示抽到的二等品件数,则 .
(2015年湖南卷理科第18题)某商场举行有奖促 销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖
(1)求顾客抽奖1次能获奖的概率.
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中 获一等奖的次数为,求的分布列和数学期望.
(2015年四川理17)某市两所中学的学生组队参加辩论赛,中学推荐了3名男生、2名女生,中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.
(1)求中学至少有1名学生入选代表队的概率
表示参赛的男生人数,求的分布列和数学期望.
(2017年山东理18)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示.通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用, 现有6名男志愿者,,,,,和4名女自愿者 ,,,,从中随机抽取5人接受甲种心理暗示,另外5人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含但不包含 的概率.
(2)用表示接受乙种心理暗示的女志愿者人数,求的分布列和数学期望.
练习1(2015天津理16)为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加. 现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(I)略;(II)设为选出的4人中种子选手的人数,求随机变量的分布列和数学期望
练习2(2014福建理18)为回馈顾客, 某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标面值之和为顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求: ①略 ②顾客所获的奖励额的分布列及数学期望
练习3(2012四川卷理科第17题)某居民小区有两个 相互独立的安全防范系统(简称系统)和.系统和系统在任意时刻发生故障的概率分别为和.
(I)略:(II)设系统在三次相互独立的检测中不发生故障的次数为随机变量ξ,求随机变量ξ的分布列和数学期望
(2018全国卷Ⅰ)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率都为,且各件产品是否为不合格品相互独立.
(1)记20件产品中恰有2件不合格品的概率为,求的最大值点.
(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的作为的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
①若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为,求;
②以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
(1)20件产品中恰有2件不合格品的概率为.
因此.
令,得.
当时,;
当时,.
所以的最大值点为.
(2)由(1)知,.
①令Y表示余下的件产品中的不合格品件数,依题意知,
,即.
所以
②若对余下的产品作检验,则这一箱产品所需要的检验费用为400元.
由于,故应该对余下的产品作检验.
微专题——二项分布的最大项
人教A版选修2-3第58页阅读材料
服从二项分布的随机变量取何值时概率最大
二项分布是应用最广泛的离散型随机变量概率模型,对与二项分布有关的一些问题的探究是很有意义的.例如,在上面的例4中,我们还可以提这样的问题: 如果某射手每次射击击中目标的概率为,每次射击的结果相互独立,那么他在次射击中,最有可能击中目标几次? 设他在次射击中,击中目标的次数为.由于射击中每次射击的结果是相互独立 的,因此).于是恰好次击中目标的概率为
,
从而 ,.
于是,当时,
当时,.
由以上分析可知,他在次射击中,最有可能次击中目标.
如果,其中,那么当由增大到时, 是怎样变化的?取何值时,最大?
如果~,则取得最大值时,= .
如果~,则取得最大值时,= .
已知当 ()取得最大值时,
的值是 .
内 容 内容 要求 离散型随机变量的分布列 有限个值的离散型随机变量的分布列的概念、性质 理解
超几何分布的概念、导出过程及其应用 理解
条件概率及事件间相互独立的概念 了解
n次独立重复实验模型、 二项分布及其应用 理解
离散型随机变量分布列的数学期望、方差及其计算 理解
正态分布 正态分布曲线的特点及其意义 了解
一.考纲解读
超几何分布
一般地,设有总数为件的两类物品,其中类有件,
从所有物品中任取件(),这件中所含类物品件数是一个离散型随机变量,
它取值为时的概率为
称上面的分布列为超几何分布列.
如果随机变量的分布列为超几何分布列,则称随机变量服从超几何分布.
(,为和中较小的一个).
超几何分布 超几何分布描述的是不放回抽样问题,随机变量为抽到的某类个体的个数.
总共个不同的元素,从中取出个元素
所有不同的取法有种
个不同的元素可以分为,两类,
若类中有个元素,则类中有个元素
记取出的个元素中类元素的个数为
超几何分布的特征是:
①考察对象分两类
②已知各类对象的个数
③从中抽取若干个个体,考察其中某类个体个数的概率分布
独立重复试验与二项分布:
一般地,如果在一次试验中事件发生的概率是,那么在次独立重复试验中,事件恰好发生次的概率为
此时我们称随机变量服从二项分布,记作:
… …
于是得到随机变量的概率分布如下:()
在次独立重复试验中这个事件发生的次数是一个随机变量;
判断随机试验是否服从二项分布的依据
1,在每一次试验中,事件发生的概率相同
2,各次试验中的事件是相互独立的
3,在每一次试验中,试验的结果只有两个,即发生,不发生
※离散型随机变量的方差
若随机变量服从参数为和的二项分布,则
()
,
【典例】一出租车司机从某饭店到火车站途中有6个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率是
(1)求这位司机遇到红灯数ξ的期望与方差.
(2)若遇上红灯,则需等待30秒,求司机总共等待时间η的期望与方差.
(1)易知司机遇上红灯次数ξ
所以,(ξ)==
(2)由已知=,所以,
.
※例题分析
为实数,则
某批件产品的次品率为,现从中任意的依次抽取件进行检验,问:
(1)当时,分别以放回和不放回的方式抽取,
恰好抽到件次品的概率是多少?
(2)根据(1)你对超几何分布与二项分布的关系有何认识?
回归教材,突破重点
【选修2-3P59B组第3题】
(1)在有放回的方式抽取中,每次抽取都是从这件产品中抽取, 从而抽到次品的概率都为0.02,可以把3次抽取看成是3次独立重复试验,这样抽到的次品数
恰好抽到1件次品的概率为
在无放回的方式抽取中,抽到的次品数X是随机变量,服从超几何分布,的分布与产品的总数有关,所以需要分三种情况分别计算:
1.当的时候,产品的总数为件,其中次品的件数为,合格品的件数为.从件产品中抽出件,其中恰好抽到件次品的概率为
3.当n=50000的时候,产品的总数为50000件,其中次品的件数为,合格品的件数为49000.从5000件产品中抽出3件,其中恰好抽到1件次品的概率为
2.当n=5000的时候,产品的总数为5000件,其中次品的件数为,合格品的件数为4900.从5000件产品中抽出3件,其中恰好抽到1件次品的概率为
(1)在有放回的方式抽取中
在无放回的方式抽取中
2.当n=5000
3.当n=50000
1.当n=500
(2)根据(1)的计算结果可以看出,当产品的总数很大时,超几何分布近似为二项分布而且随着总数的增加,这种近似的精度也在增加。
超几何分布与二项分布的联系与区别是什么?
在一个口袋中装有个红球、个白球,这些球除颜色外完全相同,一次从中摸出个球,摸到4个红球1个白球就是一等奖,求获一等奖的概率.
超几何分布
二项分布
超几何分布
二项分布
从概率分布表中发现,两种分布对应的概率相差不大
超几何分布与二项分布的联系与区别是什么?
超几何分布
二项分布
超几何分布
二项分布
现将问题数据改为个红球、个白球,其他条件不变
这时发现两种不同的分布其对应的概率之间的差距进一步缩小了,我们猜想:样本个数越大超几何分布和二项分布的对应概率相差就越小,当样本个数为无穷大时,超几何分布和二项分布的对应概率就相等,换而言之,超几何分布的极限就是二项分布.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的质量(单位:克),质量的分组区间为,, ,由此得到样本的频率分布直方图(如下图).
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设为质量超过505克的产品数量,求的分布列
(3)从该流水线上任取件产品,设为质量超过505克的产品数量,求的分布列.
经典例题
(答案:12件)
(2)重量超过505的产品数量为12件,则重量未超过505克的产品数量为28件,的取值为0,1,2,服从超几何分布,
(3)根据样本估计总体的思想,取一件产品,该产品的质量超过克的概率为 .
从流水线上任取件产品互不影响,该问题可看成2次独立重复试验,质量超过克的件数的可能取值为,,,且 即
期望为:
某调查机构对某校学生做了一个是否同意父母生“二孩”的抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是否同意父母生“二孩”,现已得知100人中同意父母生“二孩”的占,统计情况如下表:
同意 不同意 合计
男生 50
女生 40
合计 100
(1)求的值,根据以上数据,能否有的把握认为是否同意父母生“二孩”与性别有关?请说明理由;
(2)将上述调查所得的频率视为概率,现在从所有学生中,采取随机抽样的方法抽取位学生进行长期跟踪调查,记被抽取的4位学生中持“同意”态度的人数为,求的分布列及数学期望.
其中
解:(2) ,4
所以分布列为
数学期望为
3 4
(2)由题意知,持“同意”态度的学生占,即从学生中任意抽取到一名持“同意”态度的学生的概率是.
由于总体容量很大,故服从二项分布,即 从而
数学期望为
3 4
超几何分布 二项分布
区 别 超几何分布是不放回抽样问题,各次抽取不独立.随机变量为抽到某类个体的个数,超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型 二项分布的抽取是独立的,各次抽取相互独立.次独立重复试验中事件恰好发生次的概率可看作个互斥事件的和,其中每一个事件都可以看作个事件与个事件同时发生,只是发生的次序不同,其发生的概率都是
特 征 ①考查对象分两类 ②已知各类对象的个数 ③从中抽取若干个个体,考察某类个体数的概率分布 ①在每一次试验中某事件发生的概率是一个常数
②次试验不仅是在完全相同的情况下进行的重复试验,而且各次试验的结果是相互独立的;
=
联系 ,期望是相同的. 二项分布与超几何分布区别与联系
(2017年全国Ⅱ卷理科第13题)一批产品的二等品率为,从这批产品中每次随机取一件,有放回地抽取次.表示抽到的二等品件数,则 .
(2015年湖南卷理科第18题)某商场举行有奖促 销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖
(1)求顾客抽奖1次能获奖的概率.
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中 获一等奖的次数为,求的分布列和数学期望.
(2015年四川理17)某市两所中学的学生组队参加辩论赛,中学推荐了3名男生、2名女生,中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.
(1)求中学至少有1名学生入选代表队的概率
表示参赛的男生人数,求的分布列和数学期望.
(2017年山东理18)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示.通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用, 现有6名男志愿者,,,,,和4名女自愿者 ,,,,从中随机抽取5人接受甲种心理暗示,另外5人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含但不包含 的概率.
(2)用表示接受乙种心理暗示的女志愿者人数,求的分布列和数学期望.
练习1(2015天津理16)为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加. 现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(I)略;(II)设为选出的4人中种子选手的人数,求随机变量的分布列和数学期望
练习2(2014福建理18)为回馈顾客, 某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标面值之和为顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求: ①略 ②顾客所获的奖励额的分布列及数学期望
练习3(2012四川卷理科第17题)某居民小区有两个 相互独立的安全防范系统(简称系统)和.系统和系统在任意时刻发生故障的概率分别为和.
(I)略:(II)设系统在三次相互独立的检测中不发生故障的次数为随机变量ξ,求随机变量ξ的分布列和数学期望
(2018全国卷Ⅰ)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率都为,且各件产品是否为不合格品相互独立.
(1)记20件产品中恰有2件不合格品的概率为,求的最大值点.
(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的作为的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
①若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为,求;
②以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
(1)20件产品中恰有2件不合格品的概率为.
因此.
令,得.
当时,;
当时,.
所以的最大值点为.
(2)由(1)知,.
①令Y表示余下的件产品中的不合格品件数,依题意知,
,即.
所以
②若对余下的产品作检验,则这一箱产品所需要的检验费用为400元.
由于,故应该对余下的产品作检验.
微专题——二项分布的最大项
人教A版选修2-3第58页阅读材料
服从二项分布的随机变量取何值时概率最大
二项分布是应用最广泛的离散型随机变量概率模型,对与二项分布有关的一些问题的探究是很有意义的.例如,在上面的例4中,我们还可以提这样的问题: 如果某射手每次射击击中目标的概率为,每次射击的结果相互独立,那么他在次射击中,最有可能击中目标几次? 设他在次射击中,击中目标的次数为.由于射击中每次射击的结果是相互独立 的,因此).于是恰好次击中目标的概率为
,
从而 ,.
于是,当时,
当时,.
由以上分析可知,他在次射击中,最有可能次击中目标.
如果,其中,那么当由增大到时, 是怎样变化的?取何值时,最大?
如果~,则取得最大值时,= .
如果~,则取得最大值时,= .
已知当 ()取得最大值时,
的值是 .
同课章节目录
