2022年新高考数学二轮专题复习第2讲:函数的综合问题课件(36张PPT)
文档属性
| 名称 | 2022年新高考数学二轮专题复习第2讲:函数的综合问题课件(36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 08:47:36 | ||
图片预览











文档简介
(共36张PPT)
第2讲:函数的综合问题
真知真题扫描 考点考法探究
2022年新高考数学二轮专题复习
1. [2018·全国卷Ⅰ] 已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞)
C
[解析]函数g(x)=f(x)+x+a有两个零点,即方程f(x)=-x-a有两个不同的解,即函数f(x)的图像与直线y=-x-a有两个不同的交点.分别作出函数f(x)的图像与直线y=-x-a,由图可知,当-a≤1,即a≥-1时,函数f(x)的图像与直线y=-x-a有两个不同的交点,即函数g(x)有两个零点.
真知真题扫描
2. [2017·全国卷Ⅲ] 已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=( )
A.- B. C. D.1
C
真知真题扫描
[解析] ∵f(x)=x2-2x+a(ex-1+e-x+1),∴f(2-x)=(2-x)2-2(2-x)+a(e2-x-1+ex-2+1)=x2-4x+ 4-4+2x+a(e1-x+ex-1)=x2-2x+a(ex-1+e-x+1),∴f(2-x)=f(x),则直线x=1为f(x)图像的对称轴.∵f(x)有唯一零点,∴f(x)的零点只能为x=1,即f(1)=12-2×1+a(e1-1+e-1+1) =0,解得a=.
3. [2020·全国卷Ⅱ] 若2x-2y<3-x-3-y,则( )
A.ln(y-x+1)>0 B.ln(y-x+1)<0 C.ln|x-y|>0 D.ln|x-y|<0
A
真知真题扫描
[解析]方法一:设f(x)=2x-3-x,则f(x)在R上单调递增.由题知2x-3-x<2y-3-y,即f(x)1,所以ln(y-x+1)>0.
方法二:取x=0,y=1,可排除选项B,C,D.故选A.
4. [2019·全国卷Ⅱ] 设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时, f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值范围是( )
A.(-∞,] B.(-∞,] C.(-∞,] D.(-∞,]
B
真知真题扫描
[解析]由条件可推得f(x)=当x∈(1,2]时,f(x)=2f(x-1)=
4. [2019·全国卷Ⅱ] 设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时, f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值范围是( )
A.(-∞,] B.(-∞,] C.(-∞,] D.(-∞,]
B
真知真题扫描
2(x-1)(x-2)=2(x-)2-≥-,满足f(x)≥-;当x≤1时,f(x)=f(x+1)≥×(-)=-,满足f(x)≥-;当x∈(2,3]时,f(x)=2f(x-1)=4f(x-2)=4(x-2)(x-3)=4(x-)2-1≥-1,所以f(x)≥-不恒成立,此时由4(x-)2-1=-,解得x=或x=,结合图像可知当x≤时,恒有f(x)≥-.若对任意x∈(-∞,m],都有f(x)≥-,则m≤.
考点1 函数的零点
考点考法探究
例1 (1)(多选题)已知函数f(x)对于任意x∈R,均满足f(x)=f(2-x).当x≤1时,
f(x)=若函数g(x)=m|x|-2-f(x),则下列结论正确的为( )
A.若m<0,则g(x)恰有两个零点 B.若C.若0角度1 函数零点个数的判断
ABC
考点考法探究
[解析]因为f(x)=f(2-x)对任意x∈R都成立,所以函数f(x)的图像关于直线x=1对称,
先作出函数f(x)在(-∞,1]上的图像,再作出这部分图像关于直线x=1对称的图像,可得函数f(x)的图像,如图所示.令g(x)=0,得f(x)=m|x|-2.令h(x)=m|x|-2,则函数g(x)的零点个数为函数f(x)的图像与函数h(x)的图像的交点个数.
因为h(-x)=h(x),
所以函数h(x)是偶函数,
所以函数h(x)的图像关于y轴对称,且恒过定点(0,-2),
当函数h(x)的图像过点A(2,1)时,m=.
考点考法探究
过点(0,-2)作函数y=ln x(0所以切线的斜率为e,即当m=e时,函数h(x)的图像
与函数y=ln x(0对于A,若m<0,则g(x)恰有两个零点,故A正确;
对于B,若对于C,D,若0考点考法探究
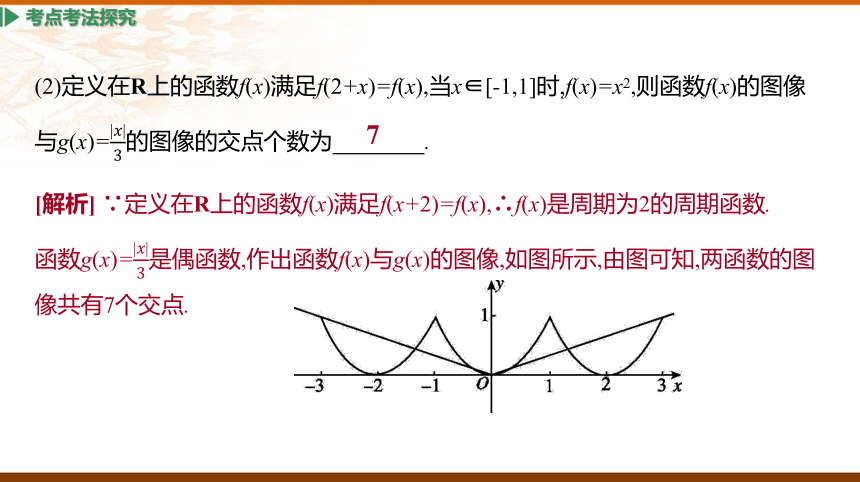
(2)定义在R上的函数f(x)满足f(2+x)=f(x),当x∈[-1,1]时,f(x)=x2,则函数f(x)的图像与g(x)=的图像的交点个数为 .
7
[解析] ∵定义在R上的函数f(x)满足f(x+2)=f(x),∴f(x)是周期为2的周期函数.
函数g(x)=是偶函数,作出函数f(x)与g(x)的图像,如图所示,由图可知,两函数的图像共有7个交点.
考点考法探究
1.关于函数f(x)=(ln x)2-2ln x,下列说法正确的是 ( )
A.函数f(x)有2个零点 B.函数f(x)有4个零点
C.e是函数f(x)的一个零点 D.2e是函数f(x)的一个零点
A
[解析]令f(x)=(ln x)2-2ln x=ln x(ln x-2)=0,可得ln x=0或ln x=2,即x=1或x=e2,所以函数f(x)有2个零点,故A正确,B不正确;
f(e)=1-2=-1≠0,所以e不是函数f(x)的一个零点,故C不正确;
f(2e)=(ln 2e)2-2ln 2e≠0,所以2e不是函数f(x)的一个零点,故D不正确.故选A.
自测题
考点考法探究
2. [2021·北京卷] 已知函数f(x)=|lg x|-kx-2,给出下列四个结论:
①若k=0,则f(x)恰有2个零点;②存在负数k,使得f(x)恰有1个零点;
③存在负数k,使得f(x)恰有3个零点;④存在正数k,使得f(x)恰有3个零点.
其中所有正确结论的序号是 .
①②④
自测题
[解析] 由题意知f(x)的零点个数即为y=|lg x|和y=kx+2的图像的交点个数,在同一个平面直角坐标系内画出y=|lg x|与y=kx+2的图像(图略).由图可知当k=0时,两函数图像有2个不同的交点,故①正确;存在负数k,使直线y=kx+2与y=|lg x|的图像相切,故②正确;当k<0时,直线y=kx+2与y=|lg x|的图像至多有2个交点,故③不正确;由图易知当k>0时,直线y=kx+2与y=|lg x|的图像可以有3个不同的交点,故④正确.故答案为①②④.
角度2 已知函数零点(个数)求参或范围
考点考法探究
例2 (1)[2021·天津卷] 设a∈R,函数f(x)=若f(x)在区间(0,+∞)内恰好有6个零点,则a的取值范围是( )
A.(2,]∪(,] B.(,2]∪(,]
C.(2,]∪[,3) D.(,2)∪[,3)
A
考点考法探究
[解析]因为二次函数最多有2个零点,所以f(x)=cos(2πx-2πa)在(0,a)内至少有4个零点.由f(x)=cos(2πx-2πa)=cos 2π(x-a)=0,得2π(x-a)=+kπ(k∈Z),整理得x=++a(k∈Z),由0<++a2时,令f(a)=a2-2a(a+1) +a2+5=0,解得a=,则当2时,f(x)在[a,+∞)内有1个零点.综上可得,a∈(2,]∪(,].故选A.
[解析]函数g(x)=f(x)-a的零点即为函数f(x)的图像与直线y=a交点的横坐标,作出f(x)的图像与直线y=a如图所示.由图可得,若函数g(x)有四
个零点xi(i=1,2,3,4),其中x1-lg x3=a,lg x4=a,∴x3=10-a,x4=10a,∴(x1+x2)(x3-x4)=-10(x3-x4)
=10(10a-10-a).∵函数y=10(10a-10-a)在(0,1]上单调递增,
∴10(10a-10-a)∈(0,99],即(x1+x2)(x3-x4)∈(0,99].故选A.
考点考法探究
(2)设函数f(x)=若函数g(x)=f(x)-a(a∈R)有四个零点
xi(i=1,2,3,4),其中x1A.(0,99] B.(0,100] C.(0,101] D.(0,+∞)
A
考点考法探究
【规律提炼】
1. 求复杂函数的零点的关键是对新函数的构建,根据新函数图像交点的个数确定原函数零点的个数.通常的原则是:一是构建两个常见初等函数,二是一个函数图像是固定的,另一个函数图像是移动的;三是参数放在直线型中,即定曲线动直线,这样便于利用数形结合解决问题.
考点考法探究
2.复合函数零点问题的特点:(1)在求关于x的方程g[f(x)]=0的根的个数时,要分为两层来分析,第一层是解关于f(x)的方程,观察有几个f(x)的值使得等式成立;第二层是结合第一层f(x)的值求出每一个f(x)与几个x对应,将x的个数汇总后即为g[f(x)]=0的根的个数.
(2)若已知零点个数求参数的范围,则先确定关于f(x)的方程g[f(x)]=0的根的个数,再根据个数与f(x)的图像特点,确定每个函数值fi(x)与几个x对应,从而确定fi(x)的取值范围,进而决定参数的范围.
考点考法探究
1.设函数f(x)=若f(x)恰有两个零点,则实数a的取值范围是( )
A.[-,] B.(-,+∞) C.(-,] D.(-∞,)
C
自测题
[解析]由y=-x3+3x,得y'=-3x2+3=-3(x+1)(x-1),所以当-10,函数y=-x3+3x单调递增,当x<-1或x>1时,y'<0,函数y=-x3+3x单调递减.当x=-1时,y=-2,当x=1时,y=2,作出函数y=-x3+3x,x∈R的图像与函数y=2x,x∈R的图像,如图所示.令y=-x3+3x=0,得x=±或x=0.因为f(x)恰有两个零点,所以f(x)的图像与x轴恰有两个交点,由图可知,实数a的取值范围是-考点考法探究
2.已知函数f(x)=|ln x|,g(x)=若关于x的方程f(x)+m=g(x)恰有三个不相等的实数解,则m的取值范围是 ( )
A.(-ln 2,0] B.[0,ln 2) C.(-2-ln 2,0] D.[0,2+ln 2)
A
自测题
[解析]设h(x)=f(x)+m,作出函数h(x)和g(x)的图像如图.当x=2时,h(2)=ln 2+m, g(2)=0,要使方程f(x)+m=g(x)恰有三个不相等的实数解,
需使h(x)与g(x)的图像恰有三个不同的交点,由图可知需
满足即解得-ln 2的取值范围是(-ln 2,0],故选A.
考点考法探究
3.已知函数f(x)=若实数a,b,c,d互不相等,且|f(a)|=|f(b)|=|f(c)|=|f(d)|,则abcd的取值范围为 .
(0,16)
自测题
[解析] ∵实数a,b,c,d互不相等,且|f(a)|=|f(b)|=|f(c)|=|f(d)|,∴|f(x)|=m有四个不同的根a,b,c,d,不妨设a0)的图像交点的横坐标,可得-(a+4)=b+4,即a+b=-8,-lnc=lnd,即lncd =0,∴cd=1.由图像可知,-4-b2-8b=-(b+4)2+16∈(0,16).
考点考法探究
考点2 不等式恒成立问题
例3 (1)已知函数f(x)=若关于x的不等式f(x)A.(,) B.(,) C.(,) D.(,)
A
[解析]作出函数f(x)的图像如图所示.f(x)0)相切时,
设切点P(x0,ln(x0+1)),y'=,可得=,解得x0=-1,此时直线y=ax+
a-的斜率为,即a=.当直线y=ax+a-与曲线y=-x2-2x-2
(x≤0)相切时,由ax+a-=-x2-2x-2,得x2+(a+2)x+a+=0,令Δ=(a+
2)2-4a-6=0,得a=或a=-(舍去).由图可知考点考法探究
例3 (1)已知函数f(x)=若关于x的不等式f(x)恒成立,则实数a的取值范围是 ( )
A.(,) B.(,) C.(,) D.(,)
A
考点考法探究
(2)已知函数f(x)对x∈R均有f(x)+2f(-x)=mx-6,若f(x)≥ln x恒成立,则实数m的取值范围是 .
(-∞,-e]
[解析]函数f(x)对x∈R均有f(x)+2f(-x)=mx-6①,将-x换为x,得f(-x)+2f(x)=-mx-6②,由①②解得f(x)=-mx-2.∵f(x)≥ln x恒成立,∴m≤-恒成立,∴只需m≤(-)min.令g(x)=-,则g'(x)=,令g'(x)=0,则x=,∴g(x)在(0,)上单调递减,在(,+∞)上单调递增,∴g(x)min=g()=-e,∴m≤-e,∴实数m的取值范围为(-∞,-e].
考点考法探究
【规律提炼】
1.对于恒成立问题,常用到以下两个结论:(1)a≥f(x)恒成立 a≥f(x)max; (2)a≤f(x)恒成立 a≤f(x)min.
2.解决恒成立问题的常用方法是依据不等式的特点,等价变形,构造函数,借助图像观察,参变分离,转化为求函数的最值问题来处理,此时要遵循“知道谁的范围,谁是变量;求谁的范围,谁是参数”的原则.
考点考法探究
已知函数f(x)=x2+2x+2-x,若不等式f(1-ax)A.(-2,2) B.(-2,2) C.(-2,2) D.(-2,2)
D
自测题
[解析]函数f(x)=x2+2x+2-x的定义域为R,且f(-x)=x2+2-x+2x=f(x),所以f(x)为偶函数.设g(x)=x2,h(x)=2x+2-x,则当x≥0时,g(x)=x2是增函数,任取x1,x2∈[0,+∞),且x1>x2,则h(x1)-h(x2)=+-(+)=-+-=(-)(1-)=(-)×.
考点考法探究
已知函数f(x)=x2+2x+2-x,若不等式f(1-ax)A.(-2,2) B.(-2,2) C.(-2,2) D.(-2,2)
D
自测题
因为x1>x2≥0,所以->0,-1>0,所以h(x1)-h(x2)>0,所以h(x)=2x+2-x在[0,+∞)上是增函数,即y=f(x)在[0,+∞)上是增函数.所以不等式f(1-ax)0和x2-ax+3>0均在R上恒成立.由x2+ax+1>0在R上恒成立,得Δ1=a2-4<0,解得-2< a<2;由x2-ax+3>0在R上恒成立,得Δ2=a2-12<0,解得-2考点3 函数同构问题
考点考法探究
例4 (1)已知0<α<,0<β<,且3α-2sin β=9β-α,则下列不等式一定成立的是( )
A.α<β2 B.α>β2 C.α>2β D.α<2β
D
[解析] 设f(x)=x-sin x,x∈(0,),则f'(x)=1-cos x>0,所以f(x)在(0,)上单调递增,所以f(x)>f(0)=0,故x>sin x,则3α+α=2sin β+9β=2sin β+32β<2β+32β.令g(x)=3x+x,所以g(α)考点考法探究
(2)已知x>0,y>0,a≥1,若a·()y+log2x=log8y3+2-x,则一定有 ( )
A.ln|1+x-3y|<0 B.ln|1+x-3y|≤0 C.ln(1+3y-x)>0 D.ln(1+3y-x)≥0
C
[解析]由题设可知,a·()3y+log2x=log2y+()x,得log2x-()x=log2y-a·()3y0,所以1+3y-x>1,则ln(1+3y-x)>ln 1=0.
考点考法探究
【规律提炼】
1.当一个式子中出现两个变量时,可以考虑适当变形,若两边结构相同,即等号或不等号左、右形式相当,一边一个变量,则考虑同构;
2.利用同构函数解题时一般都要联系到单调性或其他性质.
考点考法探究
已知实数a,b满足(a-1)5+(b-3)5=2022(1-a)3+2022(3-b)3,则a+b= .
4
自测题
[解析]因为(a-1)5+(b-3)5=2022(1-a)3+2022(3-b)3,所以(a-1)5+2022(a-1)3=(3-b)5+2022(3-b)3.令f(x)=x5+2022x3,则f(x)在R上单调递增,又f(a-1)=f(3-b),所以a-1=3-b,所以a+b=4.
[备选理由]例1考查复合函数、函数的图像、方程的根的个数,考查数形结合思想和运算求解能力;例2考查转化思想的应用;例3考查函数的性质和恒成立问题;例4考查同构问题,通过观察等式左右结构特点解题.
备用例题
例1 [配例1使用] 已知函数f(x)=g(x)=|-1|,则方程f[g(x)]=1的实数根的个数为( )
A.5 B.6 C.7 D.8
B
备用例题
[解析]作出函数f(x)的图像如图①所示,对于f[g(x)]=1,令t=g(x),则f(t)=1,则t=π+ 1或t=-π-1或t=或t=-.作出函数g(x)的图像,如图②所示,由图可知,直线y=π+1与函数g(x)的图像有2个交点,直线y=与
函数g(x)的图像有4个交点,直线y=-,
直线y=-π-1与函数g(x)的图像均没有交点.
综上可知,方程f[g(x)]=1的实数根的个数为6.故选B.
例2 [配例2使用] 已知函数f(x)=(a>0且a≠1),若函数f(x)的图像上有且仅有两个点关于y轴对称,则实数a的取值范围是( )
A.(0,1) B.(1,3) C.(0,1)∪(3,+∞) D.(0,1)∪(1,3)
D
备用例题
[解析]函数y=logax的图像与函数y=loga(-x)的图像关于y轴对称.当01时,要使函数f(x)的图像上有且仅有两个点关于y轴对称,则y=loga(-x)与y=|x+2|,-3≤x≤0的图像有且仅有一个交点,则loga3>1,∴1例3 [配例3使用] 已知函数f(x)=x2(1-),若对任意的m∈[-3,3],都有f(ma)+f(a-m+1)≥0恒成立,则实数a的取值范围为( )
A.(-∞,]∪[2,+∞) B.(-∞,-1]∪[1,+∞) C.[,2] D.[1,2]
C
备用例题
[解析]对任意的x∈R,2x+1>0,所以函数f(x)的定义域为R.由f(x)=得f(-x)====-f(x),可知函数f(x)为奇函数,f(0)=0.当x≥0时,函数g(x)=x2和h(x)=1-=均单调递增,任取x1>x2≥0,
例3 [配例3使用] 已知函数f(x)=x2(1-),若对任意的m∈[-3,3],都有f(ma)+f(a-m+1)≥0恒成立,则实数a的取值范围为( )
A.(-∞,]∪[2,+∞) B.(-∞,-1]∪[1,+∞) C.[,2] D.[1,2]
C
备用例题
则g(x1)>g(x2)≥0,h(x1)>h(x2)≥0,可得g(x1)h(x1)>g(x2)h(x2)≥0,即f(x1)>f(x2),所以函数f(x)在[0,+∞)上单调递增,则函数f(x)在(-∞,0)上也单调递增,故函数f(x)在R上单调递增.由f(ma)+f(a-m+1)≥0,得f(ma)≥-f(a-m+1)=f(m-a-1),可得ma≥m-a-1,即m(a-1)+a+1≥0.由题意可知,不等式m(a-1)+a+1≥0对任意的m∈[-3,3]恒成立,则有解得≤a≤2.故选C.
例4 [配例4使用] 已知函数f(x)是定义在R上的不恒为零的偶函数,且对任意实数x都有xf(x+1)=(x+1)f(x),则f()的值是( )
A.0 B. C.1 D.
A
备用例题
[解析]当x≠0且x≠-1时,已知条件可变形为=,从而得到等式左右的结构均为的形式,所以==…==.因为f(x)为偶函数,所以f()=f(-),又=,所以f()=f(-)=0,故=0,所以f()=0.故选A.
第2讲:函数的综合问题
真知真题扫描 考点考法探究
2022年新高考数学二轮专题复习
1. [2018·全国卷Ⅰ] 已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞)
C
[解析]函数g(x)=f(x)+x+a有两个零点,即方程f(x)=-x-a有两个不同的解,即函数f(x)的图像与直线y=-x-a有两个不同的交点.分别作出函数f(x)的图像与直线y=-x-a,由图可知,当-a≤1,即a≥-1时,函数f(x)的图像与直线y=-x-a有两个不同的交点,即函数g(x)有两个零点.
真知真题扫描
2. [2017·全国卷Ⅲ] 已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=( )
A.- B. C. D.1
C
真知真题扫描
[解析] ∵f(x)=x2-2x+a(ex-1+e-x+1),∴f(2-x)=(2-x)2-2(2-x)+a(e2-x-1+ex-2+1)=x2-4x+ 4-4+2x+a(e1-x+ex-1)=x2-2x+a(ex-1+e-x+1),∴f(2-x)=f(x),则直线x=1为f(x)图像的对称轴.∵f(x)有唯一零点,∴f(x)的零点只能为x=1,即f(1)=12-2×1+a(e1-1+e-1+1) =0,解得a=.
3. [2020·全国卷Ⅱ] 若2x-2y<3-x-3-y,则( )
A.ln(y-x+1)>0 B.ln(y-x+1)<0 C.ln|x-y|>0 D.ln|x-y|<0
A
真知真题扫描
[解析]方法一:设f(x)=2x-3-x,则f(x)在R上单调递增.由题知2x-3-x<2y-3-y,即f(x)
方法二:取x=0,y=1,可排除选项B,C,D.故选A.
4. [2019·全国卷Ⅱ] 设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时, f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值范围是( )
A.(-∞,] B.(-∞,] C.(-∞,] D.(-∞,]
B
真知真题扫描
[解析]由条件可推得f(x)=当x∈(1,2]时,f(x)=2f(x-1)=
4. [2019·全国卷Ⅱ] 设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时, f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值范围是( )
A.(-∞,] B.(-∞,] C.(-∞,] D.(-∞,]
B
真知真题扫描
2(x-1)(x-2)=2(x-)2-≥-,满足f(x)≥-;当x≤1时,f(x)=f(x+1)≥×(-)=-,满足f(x)≥-;当x∈(2,3]时,f(x)=2f(x-1)=4f(x-2)=4(x-2)(x-3)=4(x-)2-1≥-1,所以f(x)≥-不恒成立,此时由4(x-)2-1=-,解得x=或x=,结合图像可知当x≤时,恒有f(x)≥-.若对任意x∈(-∞,m],都有f(x)≥-,则m≤.
考点1 函数的零点
考点考法探究
例1 (1)(多选题)已知函数f(x)对于任意x∈R,均满足f(x)=f(2-x).当x≤1时,
f(x)=若函数g(x)=m|x|-2-f(x),则下列结论正确的为( )
A.若m<0,则g(x)恰有两个零点 B.若
ABC
考点考法探究
[解析]因为f(x)=f(2-x)对任意x∈R都成立,所以函数f(x)的图像关于直线x=1对称,
先作出函数f(x)在(-∞,1]上的图像,再作出这部分图像关于直线x=1对称的图像,可得函数f(x)的图像,如图所示.令g(x)=0,得f(x)=m|x|-2.令h(x)=m|x|-2,则函数g(x)的零点个数为函数f(x)的图像与函数h(x)的图像的交点个数.
因为h(-x)=h(x),
所以函数h(x)是偶函数,
所以函数h(x)的图像关于y轴对称,且恒过定点(0,-2),
当函数h(x)的图像过点A(2,1)时,m=.
考点考法探究
过点(0,-2)作函数y=ln x(0
与函数y=ln x(0
对于B,若
(2)定义在R上的函数f(x)满足f(2+x)=f(x),当x∈[-1,1]时,f(x)=x2,则函数f(x)的图像与g(x)=的图像的交点个数为 .
7
[解析] ∵定义在R上的函数f(x)满足f(x+2)=f(x),∴f(x)是周期为2的周期函数.
函数g(x)=是偶函数,作出函数f(x)与g(x)的图像,如图所示,由图可知,两函数的图像共有7个交点.
考点考法探究
1.关于函数f(x)=(ln x)2-2ln x,下列说法正确的是 ( )
A.函数f(x)有2个零点 B.函数f(x)有4个零点
C.e是函数f(x)的一个零点 D.2e是函数f(x)的一个零点
A
[解析]令f(x)=(ln x)2-2ln x=ln x(ln x-2)=0,可得ln x=0或ln x=2,即x=1或x=e2,所以函数f(x)有2个零点,故A正确,B不正确;
f(e)=1-2=-1≠0,所以e不是函数f(x)的一个零点,故C不正确;
f(2e)=(ln 2e)2-2ln 2e≠0,所以2e不是函数f(x)的一个零点,故D不正确.故选A.
自测题
考点考法探究
2. [2021·北京卷] 已知函数f(x)=|lg x|-kx-2,给出下列四个结论:
①若k=0,则f(x)恰有2个零点;②存在负数k,使得f(x)恰有1个零点;
③存在负数k,使得f(x)恰有3个零点;④存在正数k,使得f(x)恰有3个零点.
其中所有正确结论的序号是 .
①②④
自测题
[解析] 由题意知f(x)的零点个数即为y=|lg x|和y=kx+2的图像的交点个数,在同一个平面直角坐标系内画出y=|lg x|与y=kx+2的图像(图略).由图可知当k=0时,两函数图像有2个不同的交点,故①正确;存在负数k,使直线y=kx+2与y=|lg x|的图像相切,故②正确;当k<0时,直线y=kx+2与y=|lg x|的图像至多有2个交点,故③不正确;由图易知当k>0时,直线y=kx+2与y=|lg x|的图像可以有3个不同的交点,故④正确.故答案为①②④.
角度2 已知函数零点(个数)求参或范围
考点考法探究
例2 (1)[2021·天津卷] 设a∈R,函数f(x)=若f(x)在区间(0,+∞)内恰好有6个零点,则a的取值范围是( )
A.(2,]∪(,] B.(,2]∪(,]
C.(2,]∪[,3) D.(,2)∪[,3)
A
考点考法探究
[解析]因为二次函数最多有2个零点,所以f(x)=cos(2πx-2πa)在(0,a)内至少有4个零点.由f(x)=cos(2πx-2πa)=cos 2π(x-a)=0,得2π(x-a)=+kπ(k∈Z),整理得x=++a(k∈Z),由0<++a
[解析]函数g(x)=f(x)-a的零点即为函数f(x)的图像与直线y=a交点的横坐标,作出f(x)的图像与直线y=a如图所示.由图可得,若函数g(x)有四
个零点xi(i=1,2,3,4),其中x1
=10(10a-10-a).∵函数y=10(10a-10-a)在(0,1]上单调递增,
∴10(10a-10-a)∈(0,99],即(x1+x2)(x3-x4)∈(0,99].故选A.
考点考法探究
(2)设函数f(x)=若函数g(x)=f(x)-a(a∈R)有四个零点
xi(i=1,2,3,4),其中x1
A
考点考法探究
【规律提炼】
1. 求复杂函数的零点的关键是对新函数的构建,根据新函数图像交点的个数确定原函数零点的个数.通常的原则是:一是构建两个常见初等函数,二是一个函数图像是固定的,另一个函数图像是移动的;三是参数放在直线型中,即定曲线动直线,这样便于利用数形结合解决问题.
考点考法探究
2.复合函数零点问题的特点:(1)在求关于x的方程g[f(x)]=0的根的个数时,要分为两层来分析,第一层是解关于f(x)的方程,观察有几个f(x)的值使得等式成立;第二层是结合第一层f(x)的值求出每一个f(x)与几个x对应,将x的个数汇总后即为g[f(x)]=0的根的个数.
(2)若已知零点个数求参数的范围,则先确定关于f(x)的方程g[f(x)]=0的根的个数,再根据个数与f(x)的图像特点,确定每个函数值fi(x)与几个x对应,从而确定fi(x)的取值范围,进而决定参数的范围.
考点考法探究
1.设函数f(x)=若f(x)恰有两个零点,则实数a的取值范围是( )
A.[-,] B.(-,+∞) C.(-,] D.(-∞,)
C
自测题
[解析]由y=-x3+3x,得y'=-3x2+3=-3(x+1)(x-1),所以当-1
2.已知函数f(x)=|ln x|,g(x)=若关于x的方程f(x)+m=g(x)恰有三个不相等的实数解,则m的取值范围是 ( )
A.(-ln 2,0] B.[0,ln 2) C.(-2-ln 2,0] D.[0,2+ln 2)
A
自测题
[解析]设h(x)=f(x)+m,作出函数h(x)和g(x)的图像如图.当x=2时,h(2)=ln 2+m, g(2)=0,要使方程f(x)+m=g(x)恰有三个不相等的实数解,
需使h(x)与g(x)的图像恰有三个不同的交点,由图可知需
满足即解得-ln 2
考点考法探究
3.已知函数f(x)=若实数a,b,c,d互不相等,且|f(a)|=|f(b)|=|f(c)|=|f(d)|,则abcd的取值范围为 .
(0,16)
自测题
[解析] ∵实数a,b,c,d互不相等,且|f(a)|=|f(b)|=|f(c)|=|f(d)|,∴|f(x)|=m有四个不同的根a,b,c,d,不妨设a
考点考法探究
考点2 不等式恒成立问题
例3 (1)已知函数f(x)=若关于x的不等式f(x)
A
[解析]作出函数f(x)的图像如图所示.f(x)
设切点P(x0,ln(x0+1)),y'=,可得=,解得x0=-1,此时直线y=ax+
a-的斜率为,即a=.当直线y=ax+a-与曲线y=-x2-2x-2
(x≤0)相切时,由ax+a-=-x2-2x-2,得x2+(a+2)x+a+=0,令Δ=(a+
2)2-4a-6=0,得a=或a=-(舍去).由图可知
例3 (1)已知函数f(x)=若关于x的不等式f(x)
A.(,) B.(,) C.(,) D.(,)
A
考点考法探究
(2)已知函数f(x)对x∈R均有f(x)+2f(-x)=mx-6,若f(x)≥ln x恒成立,则实数m的取值范围是 .
(-∞,-e]
[解析]函数f(x)对x∈R均有f(x)+2f(-x)=mx-6①,将-x换为x,得f(-x)+2f(x)=-mx-6②,由①②解得f(x)=-mx-2.∵f(x)≥ln x恒成立,∴m≤-恒成立,∴只需m≤(-)min.令g(x)=-,则g'(x)=,令g'(x)=0,则x=,∴g(x)在(0,)上单调递减,在(,+∞)上单调递增,∴g(x)min=g()=-e,∴m≤-e,∴实数m的取值范围为(-∞,-e].
考点考法探究
【规律提炼】
1.对于恒成立问题,常用到以下两个结论:(1)a≥f(x)恒成立 a≥f(x)max; (2)a≤f(x)恒成立 a≤f(x)min.
2.解决恒成立问题的常用方法是依据不等式的特点,等价变形,构造函数,借助图像观察,参变分离,转化为求函数的最值问题来处理,此时要遵循“知道谁的范围,谁是变量;求谁的范围,谁是参数”的原则.
考点考法探究
已知函数f(x)=x2+2x+2-x,若不等式f(1-ax)
D
自测题
[解析]函数f(x)=x2+2x+2-x的定义域为R,且f(-x)=x2+2-x+2x=f(x),所以f(x)为偶函数.设g(x)=x2,h(x)=2x+2-x,则当x≥0时,g(x)=x2是增函数,任取x1,x2∈[0,+∞),且x1>x2,则h(x1)-h(x2)=+-(+)=-+-=(-)(1-)=(-)×.
考点考法探究
已知函数f(x)=x2+2x+2-x,若不等式f(1-ax)
D
自测题
因为x1>x2≥0,所以->0,-1>0,所以h(x1)-h(x2)>0,所以h(x)=2x+2-x在[0,+∞)上是增函数,即y=f(x)在[0,+∞)上是增函数.所以不等式f(1-ax)
考点考法探究
例4 (1)已知0<α<,0<β<,且3α-2sin β=9β-α,则下列不等式一定成立的是( )
A.α<β2 B.α>β2 C.α>2β D.α<2β
D
[解析] 设f(x)=x-sin x,x∈(0,),则f'(x)=1-cos x>0,所以f(x)在(0,)上单调递增,所以f(x)>f(0)=0,故x>sin x,则3α+α=2sin β+9β=2sin β+32β<2β+32β.令g(x)=3x+x,所以g(α)
(2)已知x>0,y>0,a≥1,若a·()y+log2x=log8y3+2-x,则一定有 ( )
A.ln|1+x-3y|<0 B.ln|1+x-3y|≤0 C.ln(1+3y-x)>0 D.ln(1+3y-x)≥0
C
[解析]由题设可知,a·()3y+log2x=log2y+()x,得log2x-()x=log2y-a·()3y
考点考法探究
【规律提炼】
1.当一个式子中出现两个变量时,可以考虑适当变形,若两边结构相同,即等号或不等号左、右形式相当,一边一个变量,则考虑同构;
2.利用同构函数解题时一般都要联系到单调性或其他性质.
考点考法探究
已知实数a,b满足(a-1)5+(b-3)5=2022(1-a)3+2022(3-b)3,则a+b= .
4
自测题
[解析]因为(a-1)5+(b-3)5=2022(1-a)3+2022(3-b)3,所以(a-1)5+2022(a-1)3=(3-b)5+2022(3-b)3.令f(x)=x5+2022x3,则f(x)在R上单调递增,又f(a-1)=f(3-b),所以a-1=3-b,所以a+b=4.
[备选理由]例1考查复合函数、函数的图像、方程的根的个数,考查数形结合思想和运算求解能力;例2考查转化思想的应用;例3考查函数的性质和恒成立问题;例4考查同构问题,通过观察等式左右结构特点解题.
备用例题
例1 [配例1使用] 已知函数f(x)=g(x)=|-1|,则方程f[g(x)]=1的实数根的个数为( )
A.5 B.6 C.7 D.8
B
备用例题
[解析]作出函数f(x)的图像如图①所示,对于f[g(x)]=1,令t=g(x),则f(t)=1,则t=π+ 1或t=-π-1或t=或t=-.作出函数g(x)的图像,如图②所示,由图可知,直线y=π+1与函数g(x)的图像有2个交点,直线y=与
函数g(x)的图像有4个交点,直线y=-,
直线y=-π-1与函数g(x)的图像均没有交点.
综上可知,方程f[g(x)]=1的实数根的个数为6.故选B.
例2 [配例2使用] 已知函数f(x)=(a>0且a≠1),若函数f(x)的图像上有且仅有两个点关于y轴对称,则实数a的取值范围是( )
A.(0,1) B.(1,3) C.(0,1)∪(3,+∞) D.(0,1)∪(1,3)
D
备用例题
[解析]函数y=logax的图像与函数y=loga(-x)的图像关于y轴对称.当0
A.(-∞,]∪[2,+∞) B.(-∞,-1]∪[1,+∞) C.[,2] D.[1,2]
C
备用例题
[解析]对任意的x∈R,2x+1>0,所以函数f(x)的定义域为R.由f(x)=得f(-x)====-f(x),可知函数f(x)为奇函数,f(0)=0.当x≥0时,函数g(x)=x2和h(x)=1-=均单调递增,任取x1>x2≥0,
例3 [配例3使用] 已知函数f(x)=x2(1-),若对任意的m∈[-3,3],都有f(ma)+f(a-m+1)≥0恒成立,则实数a的取值范围为( )
A.(-∞,]∪[2,+∞) B.(-∞,-1]∪[1,+∞) C.[,2] D.[1,2]
C
备用例题
则g(x1)>g(x2)≥0,h(x1)>h(x2)≥0,可得g(x1)h(x1)>g(x2)h(x2)≥0,即f(x1)>f(x2),所以函数f(x)在[0,+∞)上单调递增,则函数f(x)在(-∞,0)上也单调递增,故函数f(x)在R上单调递增.由f(ma)+f(a-m+1)≥0,得f(ma)≥-f(a-m+1)=f(m-a-1),可得ma≥m-a-1,即m(a-1)+a+1≥0.由题意可知,不等式m(a-1)+a+1≥0对任意的m∈[-3,3]恒成立,则有解得≤a≤2.故选C.
例4 [配例4使用] 已知函数f(x)是定义在R上的不恒为零的偶函数,且对任意实数x都有xf(x+1)=(x+1)f(x),则f()的值是( )
A.0 B. C.1 D.
A
备用例题
[解析]当x≠0且x≠-1时,已知条件可变形为=,从而得到等式左右的结构均为的形式,所以==…==.因为f(x)为偶函数,所以f()=f(-),又=,所以f()=f(-)=0,故=0,所以f()=0.故选A.
同课章节目录
