2021-2022学年北师大版九年级数学下册第一章 直角三角形边角关系 同步练习 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第一章 直角三角形边角关系 同步练习 (Word版含答案) | 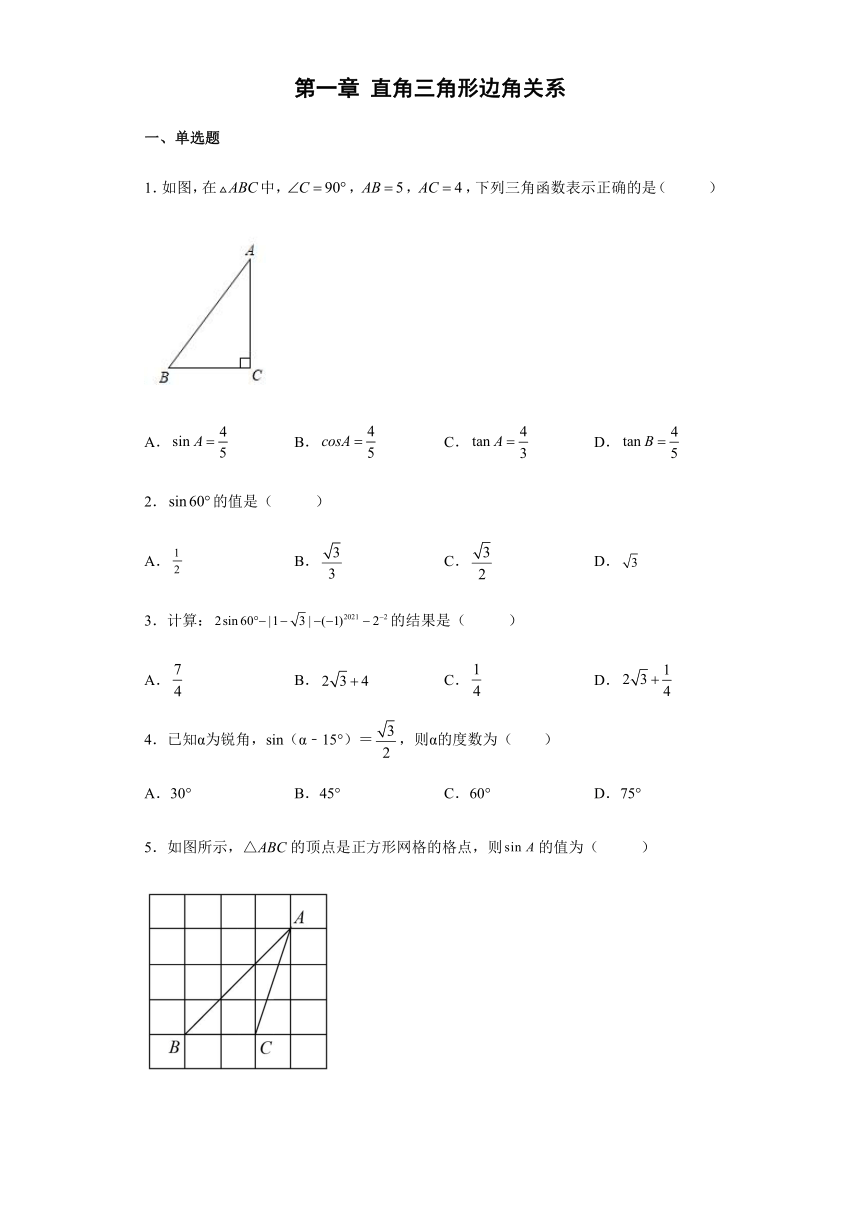 | |
| 格式 | doc | ||
| 文件大小 | 255.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 13:58:59 | ||
图片预览


文档简介
直角三角形边角关系
一、单选题
1.如图,在中,,,,下列三角函数表示正确的是( )
A. B. C. D.
2.的值是( )
A. B. C. D.
3.计算:的结果是( )
A. B. C. D.
4.已知α为锐角,sin(α﹣15°)=,则α的度数为( )
A.30° B.45° C.60° D.75°
5.如图所示,△ABC的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
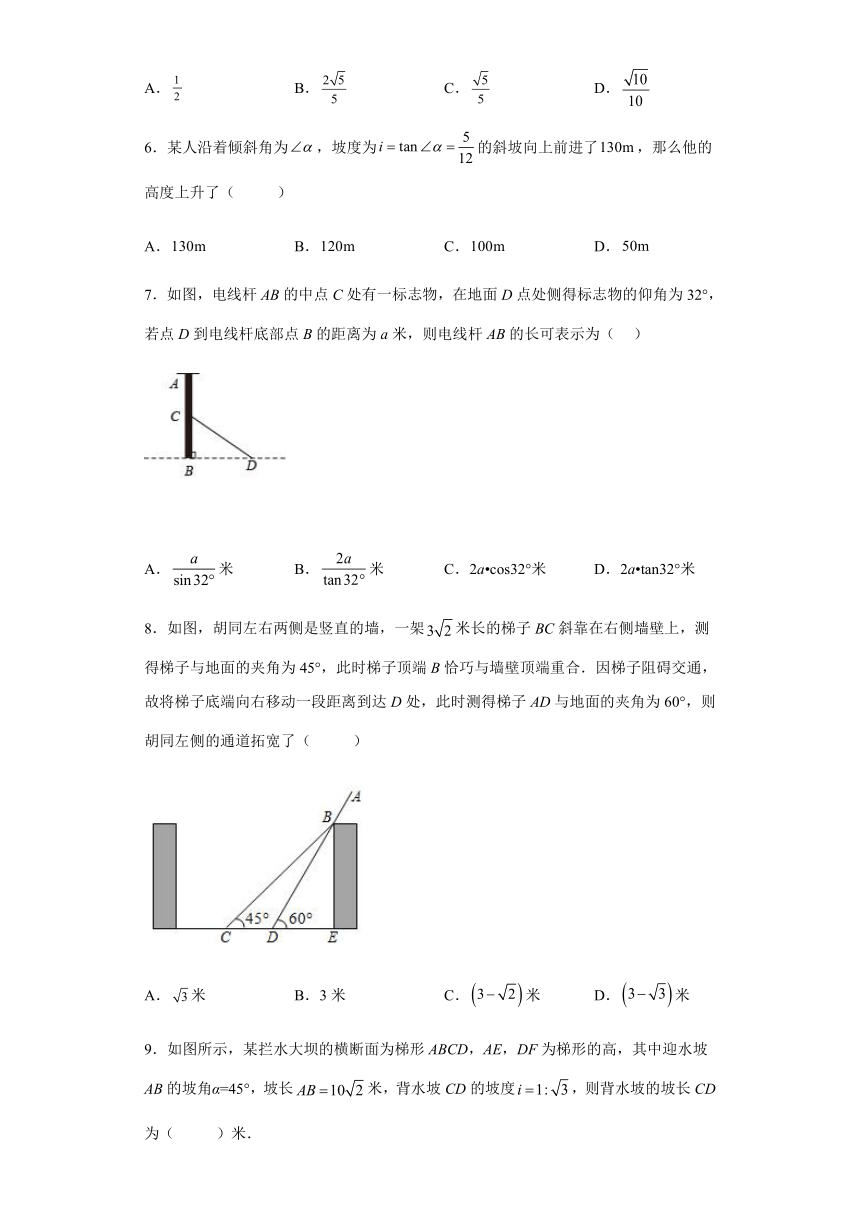
6.某人沿着倾斜角为,坡度为的斜坡向上前进了,那么他的高度上升了( )
A. B. C. D.
7.如图,电线杆AB的中点C处有一标志物,在地面D点处侧得标志物的仰角为32°,若点D到电线杆底部点B的距离为a米,则电线杆AB的长可表示为( )
A.米 B.米 C.2a cos32°米 D.2a tan32°米
8.如图,胡同左右两侧是竖直的墙,一架米长的梯子BC斜靠在右侧墙壁上,测得梯子与地面的夹角为45°,此时梯子顶端B恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达D处,此时测得梯子AD与地面的夹角为60°,则胡同左侧的通道拓宽了( )
A.米 B.3米 C.米 D.米
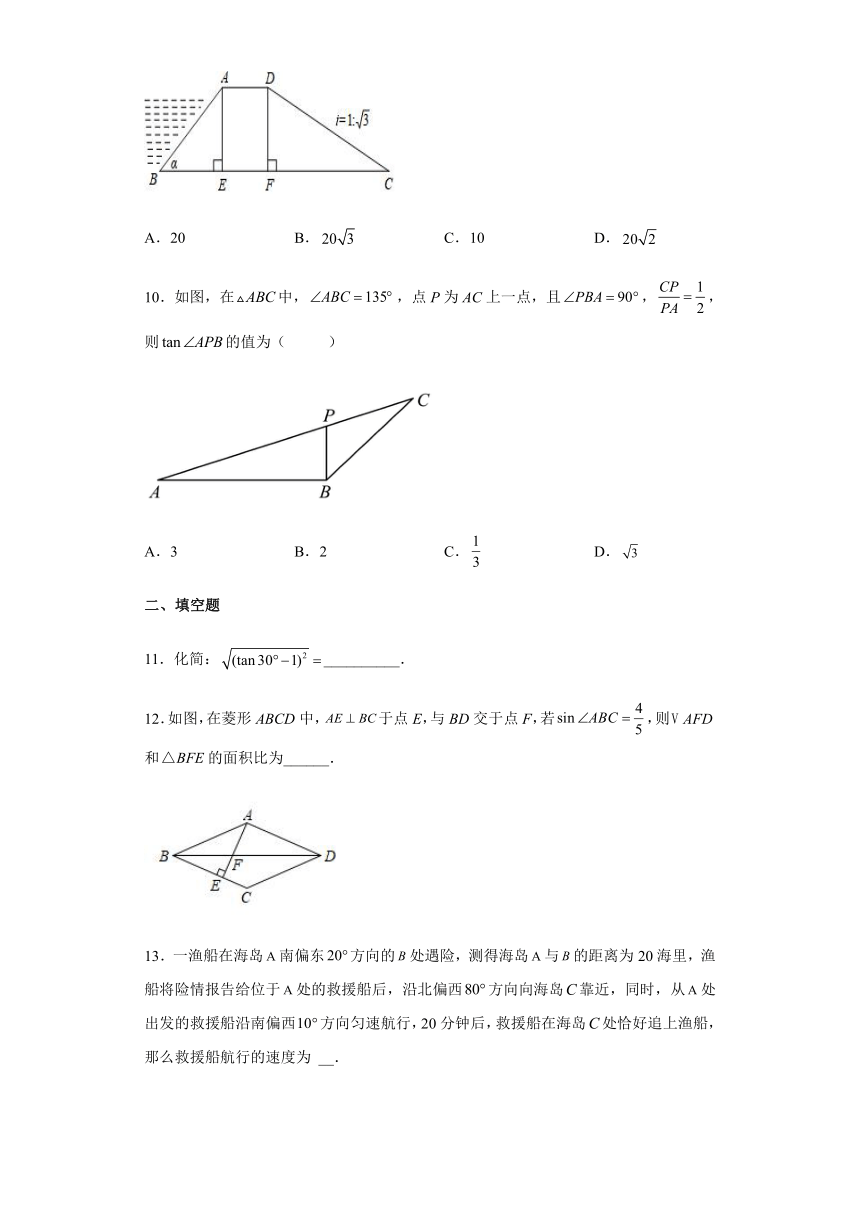
9.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长米,背水坡CD的坡度,则背水坡的坡长CD为( )米.
A.20 B. C.10 D.
10.如图,在中,,点P为AC上一点,且,,则的值为( )
A.3 B.2 C. D.
二、填空题
11.化简:__________.
12.如图,在菱形ABCD中,于点E,与BD交于点F,若,则和的面积比为______.
13.一渔船在海岛南偏东方向的处遇险,测得海岛与的距离为20海里,渔船将险情报告给位于处的救援船后,沿北偏西方向向海岛靠近,同时,从处出发的救援船沿南偏西方向匀速航行,20分钟后,救援船在海岛处恰好追上渔船,那么救援船航行的速度为 __.
14.如图ABC 中, AB 2 , BC 4 , CD AB 于 D , AE BC 于 E , 则AE : CD .
三、解答题
15.(1)计算:.
(2)计算:
16.已知在△ABC中,∠C=90°,AB=4,.
(1)求BC;
(2)求sin∠A
17.如图5,在△ABC中,∠ACB=90°,∠CAB>∠B,CD是斜边AB上的中线,过点A作∠CAE=∠B,交BC于点E,交CD于点H,且AH=2CH.
(1)求sinB的值;
(2)当CD=时,求BE的长.
18.在疫情防控工作中,某学校在校门口的大门上方安装了一个人体测温摄像头.如图,学校大门高ME=7.5米,AB为体温监测有效识别区域的长度,小明身高BD=1.5米,他站在点B处测得摄像头M的仰角为30°,站在点A处测得摄像头M的仰角为60°,求体温监测有效识别区域AB的长度.
19.图①是某小区折叠道闸的实景图,图②是其工作示意图,道闸由垂直于地面的立柱AB,CD和折叠杆“AE﹣EF”组成,其中AB=CD=1.2m,AB,CD之间的水平距离BD=2.5m,AE=1.5m.道闸工作时,折叠杆“AE﹣EF”可绕点A在一定范围内转动,张角为∠BAE(90°≤∠BAE≤150°),同时杆EF始终与地面BD保持平行.(参考数据:≈1.414,≈1.732)
(1)当张角∠BAE为135°时,求杆EF与地面BD之间的距离(结果精确到0.01m);
(2)试通过计算判断宽度为1.8m,高度为2.45m的小型厢式货车能否正常通过此道闸?
试卷第1页,共3页
答案
1.B
2.C
3.A
4.D
5.C
6.D
7.D
8.D
9.A
10.A
11.
12.
13.海里小时
14.
15.(1);(2)
16.(1)3
(2)
17.(1);
(2)
18.
19.(1)2.26米;
(2)不能
答案第1页,共2页
一、单选题
1.如图,在中,,,,下列三角函数表示正确的是( )
A. B. C. D.
2.的值是( )
A. B. C. D.
3.计算:的结果是( )
A. B. C. D.
4.已知α为锐角,sin(α﹣15°)=,则α的度数为( )
A.30° B.45° C.60° D.75°
5.如图所示,△ABC的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
6.某人沿着倾斜角为,坡度为的斜坡向上前进了,那么他的高度上升了( )
A. B. C. D.
7.如图,电线杆AB的中点C处有一标志物,在地面D点处侧得标志物的仰角为32°,若点D到电线杆底部点B的距离为a米,则电线杆AB的长可表示为( )
A.米 B.米 C.2a cos32°米 D.2a tan32°米
8.如图,胡同左右两侧是竖直的墙,一架米长的梯子BC斜靠在右侧墙壁上,测得梯子与地面的夹角为45°,此时梯子顶端B恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达D处,此时测得梯子AD与地面的夹角为60°,则胡同左侧的通道拓宽了( )
A.米 B.3米 C.米 D.米
9.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长米,背水坡CD的坡度,则背水坡的坡长CD为( )米.
A.20 B. C.10 D.
10.如图,在中,,点P为AC上一点,且,,则的值为( )
A.3 B.2 C. D.
二、填空题
11.化简:__________.
12.如图,在菱形ABCD中,于点E,与BD交于点F,若,则和的面积比为______.
13.一渔船在海岛南偏东方向的处遇险,测得海岛与的距离为20海里,渔船将险情报告给位于处的救援船后,沿北偏西方向向海岛靠近,同时,从处出发的救援船沿南偏西方向匀速航行,20分钟后,救援船在海岛处恰好追上渔船,那么救援船航行的速度为 __.
14.如图ABC 中, AB 2 , BC 4 , CD AB 于 D , AE BC 于 E , 则AE : CD .
三、解答题
15.(1)计算:.
(2)计算:
16.已知在△ABC中,∠C=90°,AB=4,.
(1)求BC;
(2)求sin∠A
17.如图5,在△ABC中,∠ACB=90°,∠CAB>∠B,CD是斜边AB上的中线,过点A作∠CAE=∠B,交BC于点E,交CD于点H,且AH=2CH.
(1)求sinB的值;
(2)当CD=时,求BE的长.
18.在疫情防控工作中,某学校在校门口的大门上方安装了一个人体测温摄像头.如图,学校大门高ME=7.5米,AB为体温监测有效识别区域的长度,小明身高BD=1.5米,他站在点B处测得摄像头M的仰角为30°,站在点A处测得摄像头M的仰角为60°,求体温监测有效识别区域AB的长度.
19.图①是某小区折叠道闸的实景图,图②是其工作示意图,道闸由垂直于地面的立柱AB,CD和折叠杆“AE﹣EF”组成,其中AB=CD=1.2m,AB,CD之间的水平距离BD=2.5m,AE=1.5m.道闸工作时,折叠杆“AE﹣EF”可绕点A在一定范围内转动,张角为∠BAE(90°≤∠BAE≤150°),同时杆EF始终与地面BD保持平行.(参考数据:≈1.414,≈1.732)
(1)当张角∠BAE为135°时,求杆EF与地面BD之间的距离(结果精确到0.01m);
(2)试通过计算判断宽度为1.8m,高度为2.45m的小型厢式货车能否正常通过此道闸?
试卷第1页,共3页
答案
1.B
2.C
3.A
4.D
5.C
6.D
7.D
8.D
9.A
10.A
11.
12.
13.海里小时
14.
15.(1);(2)
16.(1)3
(2)
17.(1);
(2)
18.
19.(1)2.26米;
(2)不能
答案第1页,共2页
