安徽省宿州市萧县城北初级中学2021-2022学年九年级下学期第一次月考数学试题(Word版无答案)
文档属性
| 名称 | 安徽省宿州市萧县城北初级中学2021-2022学年九年级下学期第一次月考数学试题(Word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 394.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 16:37:40 | ||
图片预览


文档简介
2021-2022学年安徽省宿州市萧县城北中学九年级(下)第一次月考数学试卷
一、选择题(共10小题,每题4分)
1.如图,四边形ABCD内接于⊙O,若∠A=80°,则∠C的度数是()
A.80° B.100 C.110° D.120°
2.如图是由六个棱长为1的小正方体搭成的几何体,其左视图的面积为( )
A.3 B.4 C.5 D.6
3.如图,AB是⊙O的弦,半径OC⊥AB,D是优弧AB上一点,若∠BOC=34°,则∠ADC的大小是()
A.10° B.17° C.30° D.34°
4.如图,滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A. B. C.100cos20° D.100sin20°
5.如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接A0,AC,若△AOC的面积为4,则k=( )
A.16 B.12 C.8 D.4
6.如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠ABD=54°,则∠C的度数为()
A.34° B.36° C.46° D.54°
7.如图,若△ABC内一点P,满足∠PAB=∠PBC=∠PCA=α,
①∠BAC=90°,则必有∠APC=90°;
②若AB=AC.则必有PB2=PA PC,
对于这两个结论,下列说法正确的是( )
A.①对,②错 B.①错,②对 C.①,②均对 D.①,②均错
8.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出下列结论:
①ab<0且c=0;
②b2﹣4ac>0;
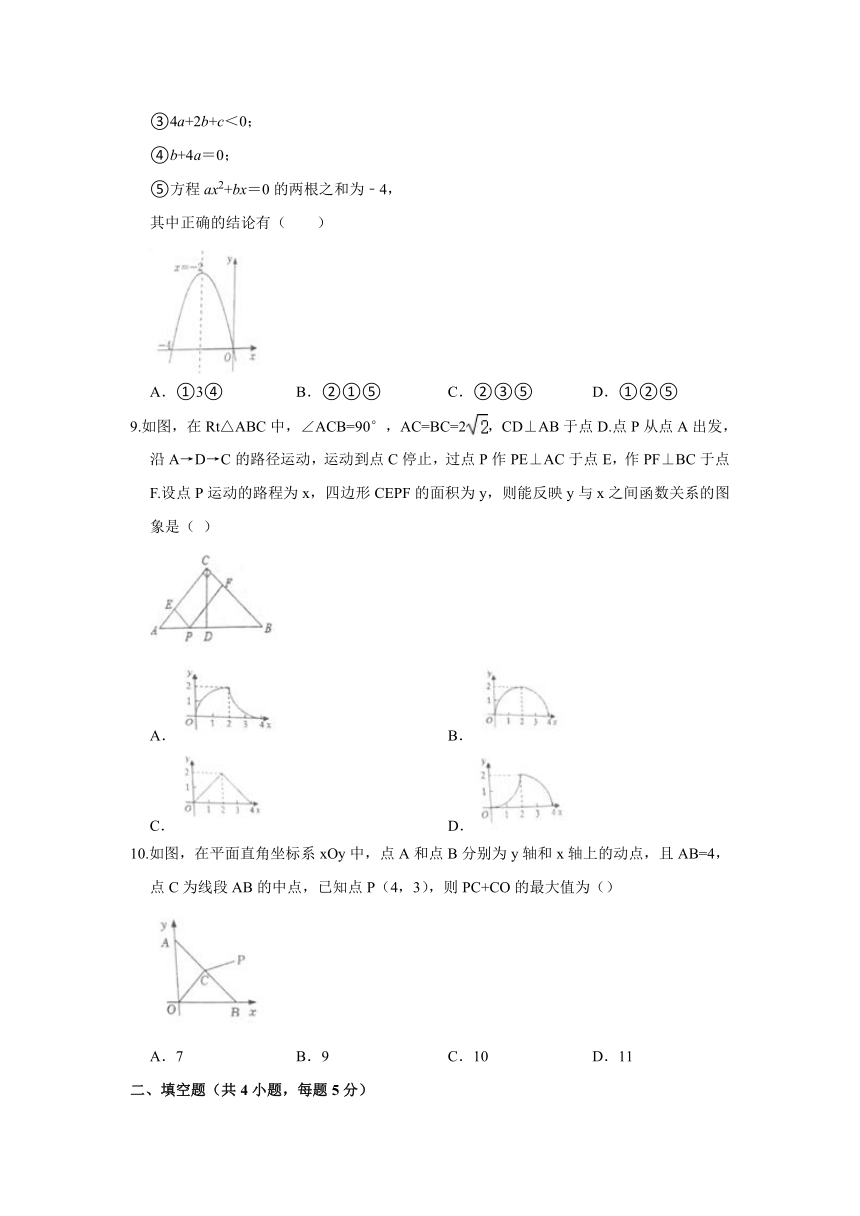
③4a+2b+c<0;
④b+4a=0;
⑤方程ax2+bx=0的两根之和为﹣4,
其中正确的结论有( )
A.①3④ B.②①⑤ C.②③⑤ D.①②⑤
9.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,CD⊥AB于点D.点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.设点P运动的路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系的图象是( )
A. B.
C. D.
10.如图,在平面直角坐标系xOy中,点A和点B分别为y轴和x轴上的动点,且AB=4,点C为线段AB的中点,已知点P(4,3),则PC+CO的最大值为()
A.7 B.9 C.10 D.11
二、填空题(共4小题,每题5分)
11.方程x2﹣2x=0的解为 .
12.在△ABC中,∠A,∠B都是锐角,若sinA=,cosB=.则△ABC的形状为 三角形.
13.如图,在平面直角坐标系xOy中,直线y=与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
14.新定义:在平面直角坐标系中,对于点P(m,n)和点P'(m,n'),若满足n'=n-4时,则称点P'(m,n')是点P(m,n)的限变点.例如:点P1(2,5)的限变点是P1'(2,1),若点P(m,n)在二次函数y=﹣x2+4x+2的图象上,则当-1≤m≤3时,其限变点P'的纵坐标n'的取值范围是
三、解答题(共9小题,15、16、17、18每题8分,19、20每题10分,21、22每题12分,23题14分)
15.计算:4sin60°﹣|﹣1|+(﹣1)0+.
16.如图,AB是⊙O的弦,OC交AB于点D,点D是弦AB(AB不是直径)的中点,若AB=8cm,CD=2cm,求⊙O的半径.
17.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1)(﹣1,1)、C(0,﹣2).
(1)点B关于坐标原点O对称的点的坐标为 ;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C1.
18.“新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、李文亮、张定字(依次记为A、B、C、D),为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上A、B、C、D四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报
(1)班长在四种卡片中随机抽到标号为C的概率为 .
(2)平平和安安两位同学抽到的卡片是不同英雄的概率是多少?(用树状图或列表法)
19.图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂AC=40cm,灯罩CD=30cm,灯臂与底座构成的∠CAB=60°.CD可以绕点C上下调节一定的角度,使用发现:当CD与水平线所成的角为30°时,台灯光线最佳,现测得点D到桌面的距离为49.6cm.请通过计算说明此时台灯光线是否为最佳?(参考数据:取1.73).
20.如图,反比例函数y=的图象与一次函数y=kx+b的图象交于A、B两点,点A的坐标为(n,6),点B的坐标为(12,1).
(1)分别求m、k、b的值.
(2)点C为y轴上一动点,若S△ABC=15,求点C的坐标.
21.如图,, OABC的对角线相交于点D,⊙O经过A、D两点,与BO的延长线相交于点E,点F为上一点,且=.连接AE、DF相交于点G,若AG=3,EG=6.
(1)求 OABC对角线AC的长;
(2)求证: OABC为矩形.
22,科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽略空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度y1(米)与小钢球运动时间x(秒)之间的函数关系如图所示:小钢球离地面高度y2(米)与它的运动时间x(秒)之间的函数关系如图中抛物线所示.
(1)直接写出y1与x之间的函数关系式;
(2)求出y2与x之间的函数关系式;
(3)小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?
23.已知A、CD为⊙O上三点.且AD=CD.
(1)如图1,延长AD至点B,使BD=AD,连接CB.
①求证:△ABC为直角三角形;
②若⊙O的半径为4,AD=5,求BC的值;
(2)如图2,若∠ADC=90°,E为⊙O上的一点,且点D,E位于AC两侧,作△ADE关于AD对称的图形△ADQ,连接QC,求证:QA2+2QD2=QC2.
一、选择题(共10小题,每题4分)
1.如图,四边形ABCD内接于⊙O,若∠A=80°,则∠C的度数是()
A.80° B.100 C.110° D.120°
2.如图是由六个棱长为1的小正方体搭成的几何体,其左视图的面积为( )
A.3 B.4 C.5 D.6
3.如图,AB是⊙O的弦,半径OC⊥AB,D是优弧AB上一点,若∠BOC=34°,则∠ADC的大小是()
A.10° B.17° C.30° D.34°
4.如图,滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A. B. C.100cos20° D.100sin20°
5.如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接A0,AC,若△AOC的面积为4,则k=( )
A.16 B.12 C.8 D.4
6.如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠ABD=54°,则∠C的度数为()
A.34° B.36° C.46° D.54°
7.如图,若△ABC内一点P,满足∠PAB=∠PBC=∠PCA=α,
①∠BAC=90°,则必有∠APC=90°;
②若AB=AC.则必有PB2=PA PC,
对于这两个结论,下列说法正确的是( )
A.①对,②错 B.①错,②对 C.①,②均对 D.①,②均错
8.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出下列结论:
①ab<0且c=0;
②b2﹣4ac>0;
③4a+2b+c<0;
④b+4a=0;
⑤方程ax2+bx=0的两根之和为﹣4,
其中正确的结论有( )
A.①3④ B.②①⑤ C.②③⑤ D.①②⑤
9.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,CD⊥AB于点D.点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.设点P运动的路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系的图象是( )
A. B.
C. D.
10.如图,在平面直角坐标系xOy中,点A和点B分别为y轴和x轴上的动点,且AB=4,点C为线段AB的中点,已知点P(4,3),则PC+CO的最大值为()
A.7 B.9 C.10 D.11
二、填空题(共4小题,每题5分)
11.方程x2﹣2x=0的解为 .
12.在△ABC中,∠A,∠B都是锐角,若sinA=,cosB=.则△ABC的形状为 三角形.
13.如图,在平面直角坐标系xOy中,直线y=与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
14.新定义:在平面直角坐标系中,对于点P(m,n)和点P'(m,n'),若满足n'=n-4时,则称点P'(m,n')是点P(m,n)的限变点.例如:点P1(2,5)的限变点是P1'(2,1),若点P(m,n)在二次函数y=﹣x2+4x+2的图象上,则当-1≤m≤3时,其限变点P'的纵坐标n'的取值范围是
三、解答题(共9小题,15、16、17、18每题8分,19、20每题10分,21、22每题12分,23题14分)
15.计算:4sin60°﹣|﹣1|+(﹣1)0+.
16.如图,AB是⊙O的弦,OC交AB于点D,点D是弦AB(AB不是直径)的中点,若AB=8cm,CD=2cm,求⊙O的半径.
17.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1)(﹣1,1)、C(0,﹣2).
(1)点B关于坐标原点O对称的点的坐标为 ;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C1.
18.“新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、李文亮、张定字(依次记为A、B、C、D),为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上A、B、C、D四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报
(1)班长在四种卡片中随机抽到标号为C的概率为 .
(2)平平和安安两位同学抽到的卡片是不同英雄的概率是多少?(用树状图或列表法)
19.图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂AC=40cm,灯罩CD=30cm,灯臂与底座构成的∠CAB=60°.CD可以绕点C上下调节一定的角度,使用发现:当CD与水平线所成的角为30°时,台灯光线最佳,现测得点D到桌面的距离为49.6cm.请通过计算说明此时台灯光线是否为最佳?(参考数据:取1.73).
20.如图,反比例函数y=的图象与一次函数y=kx+b的图象交于A、B两点,点A的坐标为(n,6),点B的坐标为(12,1).
(1)分别求m、k、b的值.
(2)点C为y轴上一动点,若S△ABC=15,求点C的坐标.
21.如图,, OABC的对角线相交于点D,⊙O经过A、D两点,与BO的延长线相交于点E,点F为上一点,且=.连接AE、DF相交于点G,若AG=3,EG=6.
(1)求 OABC对角线AC的长;
(2)求证: OABC为矩形.
22,科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽略空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度y1(米)与小钢球运动时间x(秒)之间的函数关系如图所示:小钢球离地面高度y2(米)与它的运动时间x(秒)之间的函数关系如图中抛物线所示.
(1)直接写出y1与x之间的函数关系式;
(2)求出y2与x之间的函数关系式;
(3)小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?
23.已知A、CD为⊙O上三点.且AD=CD.
(1)如图1,延长AD至点B,使BD=AD,连接CB.
①求证:△ABC为直角三角形;
②若⊙O的半径为4,AD=5,求BC的值;
(2)如图2,若∠ADC=90°,E为⊙O上的一点,且点D,E位于AC两侧,作△ADE关于AD对称的图形△ADQ,连接QC,求证:QA2+2QD2=QC2.
同课章节目录
