2021-2022学年北师大版九年级下册数学 第1章 直角三角形的边角关系 专项训练(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级下册数学 第1章 直角三角形的边角关系 专项训练(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 19:13:41 | ||
图片预览

文档简介
第1章 直角三角形的边角关系 专项训练
一、选择题:本题共20小题.
1.如图,在平面直角坐标系内有一点,连接OP,则OP与x轴正方向所夹锐角的正弦值是( )
A. B. C. D.
2.在中,,都是锐角,且,,则的形状是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
3.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到的位置,已知AO的长为4米.若栏杆的旋转角,则栏杆A端升高的高度为( )
A.米 B.米 C.米 D.米
4.如图,的顶点在正方形网格的格点上,则的值为( )
A. B. C.2 D.
5.如图,在四边形ABCD中,,,,,,则AB的长是( )
A.3 B.6 C.8 D.9
6.如图,为了测量一条河流的宽度,一测量员在河岸边相距200 m的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A. m B. m C. m D. m
7.一人乘雪橇沿坡比为的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为,若滑到坡底的时间为5 s,则此人下降的高度为( )
A. B.45 m C. D.90m
8.公元3世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形的面积是25,则( )
A. B. C. D.
9.如图,在中,,点D在AB的延长线上,连接CD,若,,则的值为( )
A.1 B.2 C. D.
10.如图,一块矩形木板ABCD斜靠在墙边(,点A,B,C,D,O在同一平面内),已知,,.则点A到OC的距离等于( )
A. B. C. D.
11.已知为锐角,且,则( )
A.30° B.45° C.60° D.90°
12.如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直(A,D,B在同一条直线上),设,则拉线BC的长度为( )
A. B. C. D.
13.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算时,如图,在中,,,延长CB使,连接AD,得,所以.类比这种方法,计算的值为( )
A. B. C. D.
14.如图,的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
15.如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为,已知,则梯子顶端上升了( )
A.1米 B.1.5米 C.2米 D.2.5米
16.图(1)是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图(2)所示的四边形OABC.若,,则的值为( )
A. B. C. D.
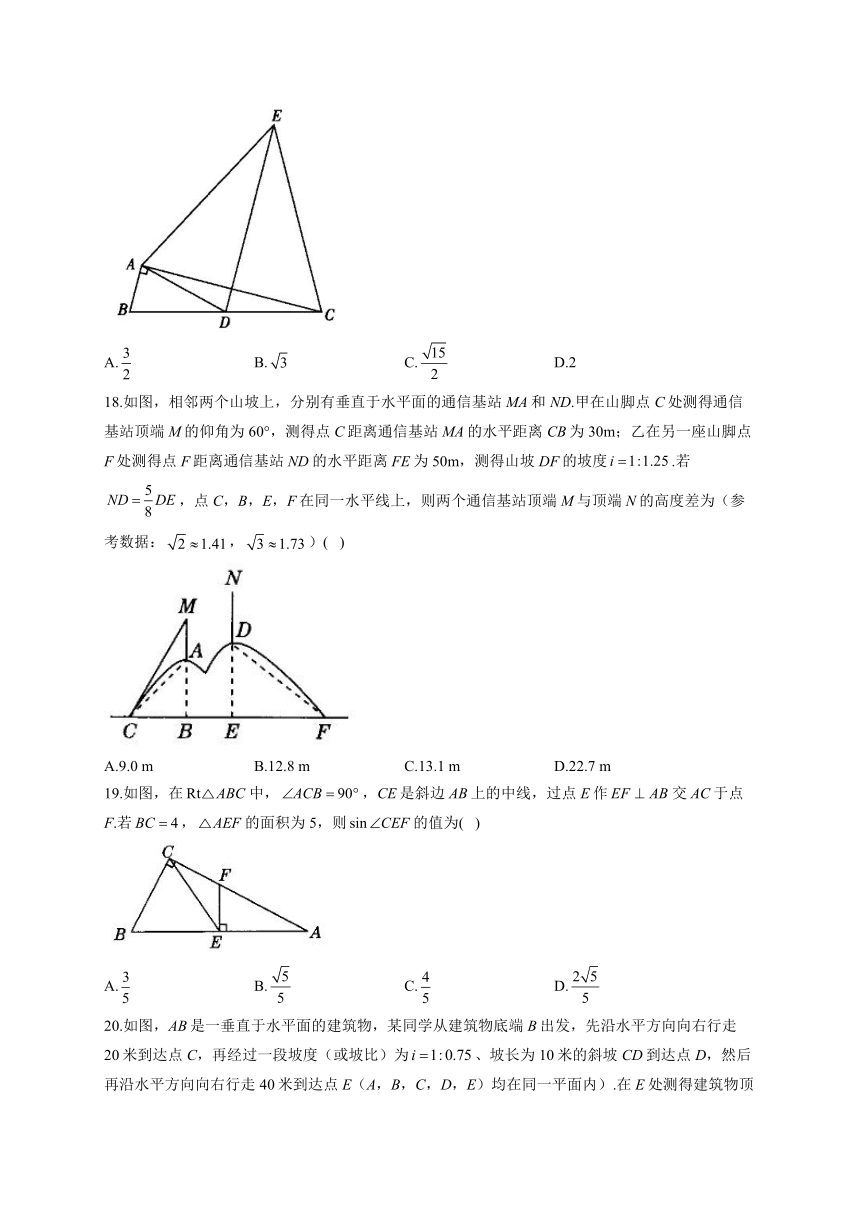
17.如图,中,,,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使,连接CE,则的值为( )
A. B. C. D.2
18.如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50m,测得山坡DF的坡度.若,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为(参考数据:,)( )
A.9.0 m B.12.8 m C.13.1 m D.22.7 m
19.如图,在中,,CE是斜边AB上的中线,过点E作交AC于点F.若,的面积为5,则的值为( )
A. B. C. D.
20.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E)均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据,,)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
二、填空题:本题共10小题.
21.在中,角A,B,C的对边分别为a,b,c,,,,则__________,___________.
22.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为___________.
23.如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若是“好玩三角形”,且,则___________.
24.如图,在中,,,垂足为点D,如果,,那么__________.
25.如图,在正方形ABCD中,E是边AD的中点.将沿直线BE翻折,点A落在点F处,连接DF,那么的正切值是____________.
26.如图,在四边形ABCD中,,,,.若,则______________.
27.如图,在中,,,则的面积=___________.
28.如图,的顶点B,C的坐标分别是,,且,,则顶点A的坐标是____________________.
29.如图,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40 km,仰角是30°,n秒后,火箭到达B点,此时在R处测得仰角是45°,则火箭在这n秒中上升的高度是____________km.
30.如图,在矩形ABCD中,BD是对角线,,垂足为E,连接CE.若,则的值为______________.
三、解答题:本题共4小题.
31.如图,,,,,求的值和点B到直线MC的距离.
32.如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来.已知,,,,汽车从A处前行多少米,才能发现C处的儿童(结果保留整数)?
(参考数据:,,;,,)
33.小明想利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选取了一点D,并在点D处安装了测倾器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使,并在点G处的地面上水平放置了一个小平面镜,小明沿BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得,小明眼睛与地面的距离,测倾器的高.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,求这棵古树的高AB(小平面镜的大小忽略不计).
34.如图,在直角梯形ABCD中,,,,,.
(1)求梯形ABCD的面积;
(2)连接BD,求的正切值.
答案解析
1.答案:D
解析:解:作轴于点M,
,
,,
由勾股定理得:,
,
故选:D
2.答案:B
解析:中,,都是锐角,,,
.
.
故选B.
3.答案:B
解析:如图,过点作于点C.
由题意知米.,米.故选B.
4.答案:A
解析:如图,点D为格点,连接BD,设网格中每个小正方形的边长为1,则,,,,.又,,.故选A.
5.答案:B
解析:,.,..,即,,.
6.答案:B
解析:在中,,,., m,即河宽 m.故选B.
7.答案:B
解析:设斜坡的坡角为.当时,.
斜坡的坡比为,..
此人下降的高度为,故选B.
8.答案:A
解析:大正方形的面积是125,小正方形的面积是25,大正方形的边长为,小正方形的边长为5.,,.故选A.
9.答案:B
解析:过点D作,交CB的延长线于点M,如图所示.
,,
.
.
,
.
在中,,
设,则.
又,
,.
.
10.答案:D
解析:过点A分别作于点E,作于点F.设AE与BC的交点为G.
四边形ABCD是矩形,,,,,,,,,故选D.
11.答案:A
解析:,故选A.
12.答案:B
解析:因为,,所以,,所以.在中,,故.故选B.
13.答案:B
解析:如图,在中,,,延长CB使,连接AD,得,
设,则,
.
14.答案:B
解析:如图,过点A作于点D.
在中,,,
.
.
15.答案:C
解析:如图,由题意可知米.在中,(米).在中,(米),(米),(米),即梯子顶端上升了2米.
16.答案:A
解析:在中,,,,.在中,由勾股定理,得,即,,故选A.
17.答案:D
解析:设DE交AC于点T,过点E作于点H,如图所示.
在中,点D是边BC的中点,
.
.
,
.
.
.
,,
.
.
.
,
.
,
.
.
.
.
.
18.答案:C
解析:由题意可知,,.在中,,.由题意可知,,,.又,,,.因此,两个通信基站顶端M与顶端N的高度差约为13.1m.
19.答案:A
解析:如图,连接BF.
是斜边AB上的中线,,
是AB的垂直平分线.
,.
,.
,
.
在中,,,
.
由题易得,
.
又,
,
.
.
.
20.答案:A
解析:如图,作交直线ED于点M,作于点N.
在中,,设,则.
,,解得(负值舍去).
,.
因为四边形BMNC是矩形,,,
.
在中,,.故选A.
21.答案:;
解析:由勾股定理得,所以,.
22.答案:m
解析:如图,过A点作于点D.
整个图形是轴对称图形,(m),m.(m).
23.答案:或
解析:①如图,在中,,CE是的中线,
设,则,,
.
②如图,在中,,BE是的中线,
设,则,,
.
故填或.
24.答案:
解析:,.,..,,根据勾股定理,得..
25.答案:2
解析:由翻折可得,.正方形ABCD中,E是AD的中点,...又是的外角,....
26.答案:
解析:,,,,,,,.
27.答案:
解析:如图,过点A作于D.在中,,即,解得..,.的面积.
28.答案:
解析:过点A作轴,垂足为点G,如图所示.
,C的坐标分别是,,
,.
.
,,
.
,,
.
,.
,.
,.
.
顶点A的坐标是.
29.答案:
解析:在中,,km,km,(km).在中,,km,km.
30.答案:
解析:本题考查矩形的性质、三角函数的定义.过点C作,垂足为F.由题意可得,设...
31.答案:点B到直线MC的距离为
解析:,,,
.
.
过点B作于点D.
,
.
,即.
,
即点B到直线MC的距离为.
32.答案:汽车从A处前行6 m才能发现C处的儿童.
解析:在中,.
,,
,.
在中,,
.
答:汽车从A处前行6 m才能发现C处的儿童.
33.答案:这棵古树的高AB为18 m
解析:如图,过点C作于点H,
则,.
在中,,
.
.
,,
.
由题意知,
.
,即,
解得.
.
答:这棵古树的高AB为18 m.
34.答案:(1)39
(2)
解析:(1)如图,过点C作于点E.
,,
.
.
四边形ADCE是矩形.
,.
.
,
.
梯形ABCD的面积为.
(2)如图,过点C作于点H.
,
,
又,
.
.
,
,
解得.
.
.
一、选择题:本题共20小题.
1.如图,在平面直角坐标系内有一点,连接OP,则OP与x轴正方向所夹锐角的正弦值是( )
A. B. C. D.
2.在中,,都是锐角,且,,则的形状是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
3.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到的位置,已知AO的长为4米.若栏杆的旋转角,则栏杆A端升高的高度为( )
A.米 B.米 C.米 D.米
4.如图,的顶点在正方形网格的格点上,则的值为( )
A. B. C.2 D.
5.如图,在四边形ABCD中,,,,,,则AB的长是( )
A.3 B.6 C.8 D.9
6.如图,为了测量一条河流的宽度,一测量员在河岸边相距200 m的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A. m B. m C. m D. m
7.一人乘雪橇沿坡比为的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为,若滑到坡底的时间为5 s,则此人下降的高度为( )
A. B.45 m C. D.90m
8.公元3世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形的面积是25,则( )
A. B. C. D.
9.如图,在中,,点D在AB的延长线上,连接CD,若,,则的值为( )
A.1 B.2 C. D.
10.如图,一块矩形木板ABCD斜靠在墙边(,点A,B,C,D,O在同一平面内),已知,,.则点A到OC的距离等于( )
A. B. C. D.
11.已知为锐角,且,则( )
A.30° B.45° C.60° D.90°
12.如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直(A,D,B在同一条直线上),设,则拉线BC的长度为( )
A. B. C. D.
13.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算时,如图,在中,,,延长CB使,连接AD,得,所以.类比这种方法,计算的值为( )
A. B. C. D.
14.如图,的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
15.如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为,已知,则梯子顶端上升了( )
A.1米 B.1.5米 C.2米 D.2.5米
16.图(1)是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图(2)所示的四边形OABC.若,,则的值为( )
A. B. C. D.
17.如图,中,,,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使,连接CE,则的值为( )
A. B. C. D.2
18.如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50m,测得山坡DF的坡度.若,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为(参考数据:,)( )
A.9.0 m B.12.8 m C.13.1 m D.22.7 m
19.如图,在中,,CE是斜边AB上的中线,过点E作交AC于点F.若,的面积为5,则的值为( )
A. B. C. D.
20.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E)均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据,,)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
二、填空题:本题共10小题.
21.在中,角A,B,C的对边分别为a,b,c,,,,则__________,___________.
22.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为___________.
23.如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若是“好玩三角形”,且,则___________.
24.如图,在中,,,垂足为点D,如果,,那么__________.
25.如图,在正方形ABCD中,E是边AD的中点.将沿直线BE翻折,点A落在点F处,连接DF,那么的正切值是____________.
26.如图,在四边形ABCD中,,,,.若,则______________.
27.如图,在中,,,则的面积=___________.
28.如图,的顶点B,C的坐标分别是,,且,,则顶点A的坐标是____________________.
29.如图,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40 km,仰角是30°,n秒后,火箭到达B点,此时在R处测得仰角是45°,则火箭在这n秒中上升的高度是____________km.
30.如图,在矩形ABCD中,BD是对角线,,垂足为E,连接CE.若,则的值为______________.
三、解答题:本题共4小题.
31.如图,,,,,求的值和点B到直线MC的距离.
32.如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来.已知,,,,汽车从A处前行多少米,才能发现C处的儿童(结果保留整数)?
(参考数据:,,;,,)
33.小明想利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选取了一点D,并在点D处安装了测倾器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使,并在点G处的地面上水平放置了一个小平面镜,小明沿BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得,小明眼睛与地面的距离,测倾器的高.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,求这棵古树的高AB(小平面镜的大小忽略不计).
34.如图,在直角梯形ABCD中,,,,,.
(1)求梯形ABCD的面积;
(2)连接BD,求的正切值.
答案解析
1.答案:D
解析:解:作轴于点M,
,
,,
由勾股定理得:,
,
故选:D
2.答案:B
解析:中,,都是锐角,,,
.
.
故选B.
3.答案:B
解析:如图,过点作于点C.
由题意知米.,米.故选B.
4.答案:A
解析:如图,点D为格点,连接BD,设网格中每个小正方形的边长为1,则,,,,.又,,.故选A.
5.答案:B
解析:,.,..,即,,.
6.答案:B
解析:在中,,,., m,即河宽 m.故选B.
7.答案:B
解析:设斜坡的坡角为.当时,.
斜坡的坡比为,..
此人下降的高度为,故选B.
8.答案:A
解析:大正方形的面积是125,小正方形的面积是25,大正方形的边长为,小正方形的边长为5.,,.故选A.
9.答案:B
解析:过点D作,交CB的延长线于点M,如图所示.
,,
.
.
,
.
在中,,
设,则.
又,
,.
.
10.答案:D
解析:过点A分别作于点E,作于点F.设AE与BC的交点为G.
四边形ABCD是矩形,,,,,,,,,故选D.
11.答案:A
解析:,故选A.
12.答案:B
解析:因为,,所以,,所以.在中,,故.故选B.
13.答案:B
解析:如图,在中,,,延长CB使,连接AD,得,
设,则,
.
14.答案:B
解析:如图,过点A作于点D.
在中,,,
.
.
15.答案:C
解析:如图,由题意可知米.在中,(米).在中,(米),(米),(米),即梯子顶端上升了2米.
16.答案:A
解析:在中,,,,.在中,由勾股定理,得,即,,故选A.
17.答案:D
解析:设DE交AC于点T,过点E作于点H,如图所示.
在中,点D是边BC的中点,
.
.
,
.
.
.
,,
.
.
.
,
.
,
.
.
.
.
.
18.答案:C
解析:由题意可知,,.在中,,.由题意可知,,,.又,,,.因此,两个通信基站顶端M与顶端N的高度差约为13.1m.
19.答案:A
解析:如图,连接BF.
是斜边AB上的中线,,
是AB的垂直平分线.
,.
,.
,
.
在中,,,
.
由题易得,
.
又,
,
.
.
.
20.答案:A
解析:如图,作交直线ED于点M,作于点N.
在中,,设,则.
,,解得(负值舍去).
,.
因为四边形BMNC是矩形,,,
.
在中,,.故选A.
21.答案:;
解析:由勾股定理得,所以,.
22.答案:m
解析:如图,过A点作于点D.
整个图形是轴对称图形,(m),m.(m).
23.答案:或
解析:①如图,在中,,CE是的中线,
设,则,,
.
②如图,在中,,BE是的中线,
设,则,,
.
故填或.
24.答案:
解析:,.,..,,根据勾股定理,得..
25.答案:2
解析:由翻折可得,.正方形ABCD中,E是AD的中点,...又是的外角,....
26.答案:
解析:,,,,,,,.
27.答案:
解析:如图,过点A作于D.在中,,即,解得..,.的面积.
28.答案:
解析:过点A作轴,垂足为点G,如图所示.
,C的坐标分别是,,
,.
.
,,
.
,,
.
,.
,.
,.
.
顶点A的坐标是.
29.答案:
解析:在中,,km,km,(km).在中,,km,km.
30.答案:
解析:本题考查矩形的性质、三角函数的定义.过点C作,垂足为F.由题意可得,设...
31.答案:点B到直线MC的距离为
解析:,,,
.
.
过点B作于点D.
,
.
,即.
,
即点B到直线MC的距离为.
32.答案:汽车从A处前行6 m才能发现C处的儿童.
解析:在中,.
,,
,.
在中,,
.
答:汽车从A处前行6 m才能发现C处的儿童.
33.答案:这棵古树的高AB为18 m
解析:如图,过点C作于点H,
则,.
在中,,
.
.
,,
.
由题意知,
.
,即,
解得.
.
答:这棵古树的高AB为18 m.
34.答案:(1)39
(2)
解析:(1)如图,过点C作于点E.
,,
.
.
四边形ADCE是矩形.
,.
.
,
.
梯形ABCD的面积为.
(2)如图,过点C作于点H.
,
,
又,
.
.
,
,
解得.
.
.
