2021-2022学年北师大版九年级数学下册综合单元测练题(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册综合单元测练题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:04:13 | ||
图片预览




文档简介
(
20
2
1
-20
2
2
学年度第二学期
)九年级数学单元测练题(四)
(综 合)
班级_________ 姓名 座号 成绩
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的.
1.与2021和为0的数是( )
A.2021 B.0 C.-2021 D.
(
第2题图
)如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形
中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )
B. C. D.
3.若化成最简二次根式后,能与合并,则a的值不可以是( )
A. B.8 C.18 D.28
4.下列计算正确的是( )
A.a-(b+c)=a-b+c B.
C. D.
5.从小到大的一组数据-1,1,2,x,6,8的中位数为2,则这组数据的众数和平均数分别是( )
(
第6题图
)A.2,4 B.2,3 C.1,4 D.1,3
6.如图,将三角板的直角顶点放在直尺的一边上.若∠1=65°,
则∠2的度数为( )
A.15° B.35° C.25° D.40°
7.已知关于x的一元二次方程的两个实数根分别为,,且,则k的值是( )
A.-2 B.2 C.-1 D.1
(
第
8
题图
)8.如图,正六边形ABCDEF的边长为2,以A为圆心,AC的长为半径画弧,得,连接AC,AE,则图中阴影部分的面积为( )
A. B.
C. D.
(
第
9
题图
)在Rt△ABC中,∠CAB=90°,AB=8,AC=3,两顶点A,B在y轴、x轴
上滑动,点C在第一象限内,连接OC,则OC的最大值为( )
A.7 B.8
C.9 D.
已知抛物线,抛物线与x轴
交于(m,0),(n,0)两点(m<n),则m,n,,的大小关系是( )
A.<m<n< B.m<<<n
C.m<<n< D.<m<<n
二、填空题(本大题7小题,每小题4分,共28分)请将下列各题的正确答案填在该题的横线上.
11.计算:+ sin45°﹣= .
12.因式分解:= .
13.接种疫苗是防控新冠疫情最有效的手段之一,截至2021年6月19日,我国31个省区市累计接种新冠疫苗已突破10亿剂次.将数据10亿用科学记数法表示为 .
14.去分母解关于x的方程时产生增根,则m的值为 .
(
第
15
题图
)15.如图,D、E分别是△ABC边AB,AC上的点,∠AED=∠B,
若AD=1,BD=AC=3,则AE的长是 .
16.某种细菌在培养过程中,每半小时分裂1次,每次一分为二,
若这种细菌由一个分裂到16个,那么这个过程要经过 分钟.
(
第17题图
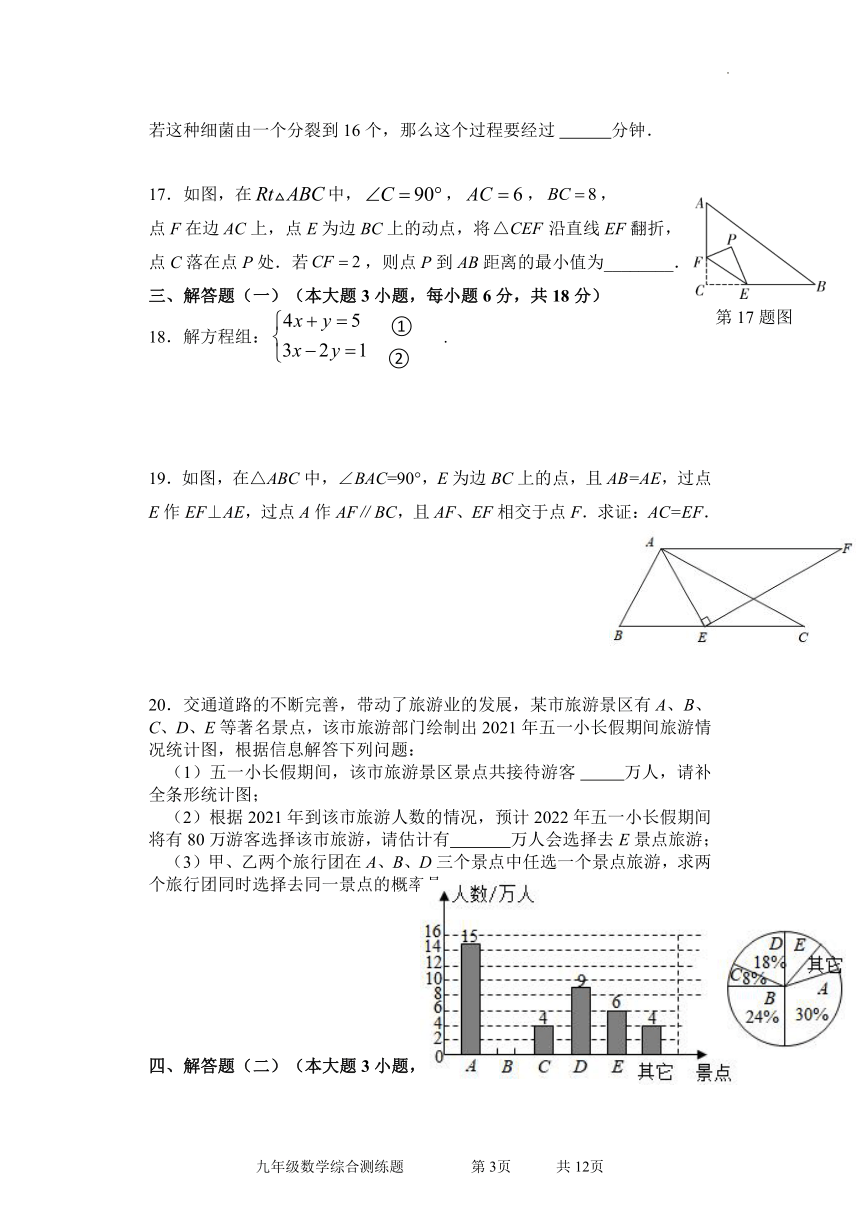
)17.如图,在中,,,,
点F在边AC上,点E为边BC上的动点,将沿直线EF翻折,
点C落在点P处.若,则点P到AB距离的最小值为________.
三、解答题(一)(本大题3小题,每小题6分,共18分)
(
①
②
)18.解方程组: . .
19.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.求证:AC=EF.
20.交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门绘制出2021年五一小长假期间旅游情况统计图,根据信息解答下列问题:
(1)五一小长假期间,该市旅游景区景点共接待游客 万人,请补全条形统计图;
(2)根据2021年到该市旅游人数的情况,预计2022年五一小长假期间将有80万游客选择该市旅游,请估计有 万人会选择去E景点旅游;
(3)甲、乙两个旅行团在A、B、D三个景点中任选一个景点旅游,求两个旅行团同时选择去同一景点的概率是 .
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.2020年上半年受到新冠状肺炎疫情的影响,汽车销售行业处于不景气状态,2020年下半年合肥某汽车销售公司推行了一种新型低能耗汽车,于2020年10月份销售该型号汽车20辆,由于该型号汽车经济适用性强,销量快速上升,12月份该公司销售该型号汽车达45辆.
(1)求11月份和12月份的平均增长率;
(2)该型号汽车每辆的进价为10万元,且销售a辆汽车,汽车厂对销售公司每辆返利0.03a万元,该公司这种型号汽车的售价为11万元/辆,若使2021年1月份每辆汽车盈利不低于2.6万元,那么该公司1月份至少需要销售该型号汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
22.如图,在菱形ABCD中,对角线AC、BD相交于点M,⊙O经过点B,C,交对角线BD于点E,且,连接OE交BC于点F.
(1)试判断AB与⊙O的位置关系,并说明理由;
(2)若BD=,tan∠CBD=,求⊙O的半径.
23.如图,反比例函数(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=.
(1)求m的值;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数(x>0)的图象恰好经过DC的中点E,求直线AE的函数表达式;
(3)若直线AE与x轴交于点M,与y轴交于点N,问线段AN与线段ME的大小关系如何?请说明理由.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”;对角线相等的凸四边形叫做“对等四边形”.
(1)在“①平行四边形;②矩形;③菱形;④正方形”中一定是“十字形”的有 ;一定是“对等四边形”的有 ;(请填序号)
(2)如图1:若凸四边形ABCD是“十字形”也是“对等四边形”,F,H,G,M分别是AD,DC,AB,BC的中点,求证:四边形FGMH为正方形;
(3)如图2,在Rt△ABC中,∠B=90°,∠C=30°,AC=20,点D从点C出发沿CA方向以2个单位每秒向A匀速运动;同时点E从A出发沿AB方向以1个单位每秒向B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,DF∥AB,连接EF,是否存在时间t(秒),使得四边形ADFE为“十字形”或“对等四边形”,若存在,请求出t的值,若不存在,请说明理由.
25.如图,已知抛物线与x轴交于点A、B,与y轴交于点C,点P是抛物线上一动点,连接PB,PC.
(1)点A的坐标为 ,点B的坐标为 ;
(2)如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;
(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.
(四)(综 合)
一、选择题:
1.C 2.B 3.D 4.B 5.B 6.C 7.D 8.A 9.C 10.A
二、填空题:
11.-2 12.y(x+3)(x﹣3) 13. 14.-1 15. 16.120 17.
三、解答题(一):
18.略. .
19.∵AF∥BC, ∴∠AEB=∠EAF,
∵AB=AE, ∴∠ABC=∠AEB, ∴∠ABC=∠EAF,
∵EF⊥AE,∠BAC=90°, ∴∠BAC=∠AEF=90°,
在△ABC和△EAF中,∠BAC=∠AEF AB=AE ∠ABC=∠EAF,
∴△ABC≌△EAF, ∴AC=EF.
20.(1)50,补全条形统计图略;(2)9.6(3)
四、解答题(二):
21.(1)设11月份和12月份的平均增长率为x,
依题意得:, 解得:,(不合题意,舍去).
(2)依题意得:11-10+0.03a≥2.6, 解得:a≥53.
又∵a为整数, ∴a可取的最小值为54,
∴此时总盈利为54×(11-10+0.03×54)=141.48(万元).
22.(1)AB是⊙O的切线.
理由:连接OB, ∵OE=OB, ∴∠OEB=∠OBE,
∵四边形ABCD是菱形,AC、BD是其对角线, ∴∠ABD=∠CBD,
∵,OE是⊙O的半径, ∴OE⊥BC,
∴∠BFE=90°, ∴∠OEB+∠CBE=90°, ∴∠ABD+∠OBE=90°,
∴OB⊥AB,即AB是⊙O的切线;
(2)∵四边形ABCD是菱形,AC、BD是其对角线,BD= ∴BM=BD=,AC⊥BD,
∵tan∠CBD=, ∴CM=BM=, ∴BC=,
∵,OE是⊙O的半径, ∴BF=BC=4,
∵tan∠CBD=,OE⊥BC, ∴EF=BF=2,
设⊙O的半径为r,则OF的长为(r-2),
在Rt△OFB中,, 即,
解得:r=5, ∴⊙O的半径为5.
23.(1)∵B(2,0), ∴OB=2,
∵tan∠AOB=, ∴AB=3, ∴A(2,3),
∵反比例函数(x>0)的图象经过线段OA的端点A, ∴m=2×3=6;
(2)∵A(2,3),B(2,0), ∴线段AB的中点纵坐标为,
∵将线段AB沿x轴正方向平移到线段DC的位置, ∴线段CD的中点E的纵坐标为,
由(1)可知反比例函数解析式为,当y=时,可得,
解得x=4, ∴E(4,),
设直线AE解析式为y=kx+b, 把A、E坐标代入可得,解得,
∴直线AE的函数表达式为;
(3)相等.
理由:在,令y=0可解得x=6,令x=0可解得y=
∴M(6,0),N(0,),且A(2,3),E(4,),
∴AN=,ME=, ∴AN=ME.
五、解答题(三):
24.(1)③④,②④;
(2)如图,∵凸四边形ABCD是“十字形”也是“对等四边形”, ∴AC=BD,AC⊥BD,
∵AC⊥BD, ∴∠AEB=90°,
∵F,H,G,M分别是AD,DC,AB,BC的中点,
∴FH=AC,GM=AC,FG=BD,MH=BD,GM∥AC,FG∥BD,
∴四边形NGPE是平行四边形, ∴∠AEB=∠FGP=90°,
∵AC=BD, ∴FH=FG=GM=MH, ∴四边形FGMH菱形,
∵∠FGP=90°, ∴菱形FGMH是正方形;
(3)存在t=,使得四边形ADFE为“十字形”.
连接AF,DE, 由题意得:CD=2t,AE=t,则AD=20-2t,
Rt△ABC中,∠C=30°,∠B=90°,AC=20, ∴AB=AC=10,
∵DF∥AB, ∴∠DFC=∠B=90°, ∴DF=CD=t,
∴DF=AE, ∴四边形ADFE是平行四边形,
∵∠A=60°, ∴ADFE不可能是矩形,
当AD=DF时,ADFE是菱形,则AF⊥DE,此时ADFE是“十字形”,
∴t=20-2t, ∴t=,
∴当t=时,四边形ADFE为“十字形”.
25.(1)(-1,0),(3,0);
(2)在中, 当x=0时,y=3, ∴C(0,3).
设直线BC的解析式为y=kx+b,
将B(3,0),C(0,3)代入,得:,解得,
∴直线BC的解析式为y= -x+3,
若PE=2ED,则PD=3ED, 设P(m,),
∵PD⊥x轴于点D, ∴E(m,-m+3),
∴=3(-m+3), ∴,
解得,(舍), ∴m=2, 此时P(2,3),E(2,1),
∴PE=2, ∴. ∴△PBC的面积为3;
(3)∵△PBC是以BC为直角边的直角三角形,
∴有两种情况:
①点C为直角顶点,过点C作直线P1C⊥BC,交抛物线于点P1,交x轴于点D,连接P1B,
∵B(3,0),C(0,3), ∴OB=OC=3, ∴∠BCO=∠OBC=45°.
∵P1C⊥BC, ∴∠DCB=90°, ∴∠DCO=45°,
又∵∠DOC=90°, ∴∠ODC=45°=∠DCO, ∴OD=OC=3,
∴D(-3,0), ∴直线P1C的解析式为y=x+3,
联立,解得或(舍); ∴P1(1,4);
②点B为直角顶点,过点B作直线BP2⊥BC,交抛物线于点P2,交y轴于点E,连接P2C,
∵P1C⊥BC,BP2⊥BC, ∴P1C∥BP2,
∴设直线BP2的解析式为y=x+b,
将B(3,0)代入,得0=3+b, ∴b= -3,
∴直线BP2的解析式为y=x-3,
联立,解得或(舍), ∴P2(-2,-5).
综上,点P的坐标为(1,4)或(-2,-5).
九年级数学综合测练题 第8页 共8页
20
2
1
-20
2
2
学年度第二学期
)九年级数学单元测练题(四)
(综 合)
班级_________ 姓名 座号 成绩
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的.
1.与2021和为0的数是( )
A.2021 B.0 C.-2021 D.
(
第2题图
)如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形
中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )
B. C. D.
3.若化成最简二次根式后,能与合并,则a的值不可以是( )
A. B.8 C.18 D.28
4.下列计算正确的是( )
A.a-(b+c)=a-b+c B.
C. D.
5.从小到大的一组数据-1,1,2,x,6,8的中位数为2,则这组数据的众数和平均数分别是( )
(
第6题图
)A.2,4 B.2,3 C.1,4 D.1,3
6.如图,将三角板的直角顶点放在直尺的一边上.若∠1=65°,
则∠2的度数为( )
A.15° B.35° C.25° D.40°
7.已知关于x的一元二次方程的两个实数根分别为,,且,则k的值是( )
A.-2 B.2 C.-1 D.1
(
第
8
题图
)8.如图,正六边形ABCDEF的边长为2,以A为圆心,AC的长为半径画弧,得,连接AC,AE,则图中阴影部分的面积为( )
A. B.
C. D.
(
第
9
题图
)在Rt△ABC中,∠CAB=90°,AB=8,AC=3,两顶点A,B在y轴、x轴
上滑动,点C在第一象限内,连接OC,则OC的最大值为( )
A.7 B.8
C.9 D.
已知抛物线,抛物线与x轴
交于(m,0),(n,0)两点(m<n),则m,n,,的大小关系是( )
A.<m<n< B.m<<<n
C.m<<n< D.<m<<n
二、填空题(本大题7小题,每小题4分,共28分)请将下列各题的正确答案填在该题的横线上.
11.计算:+ sin45°﹣= .
12.因式分解:= .
13.接种疫苗是防控新冠疫情最有效的手段之一,截至2021年6月19日,我国31个省区市累计接种新冠疫苗已突破10亿剂次.将数据10亿用科学记数法表示为 .
14.去分母解关于x的方程时产生增根,则m的值为 .
(
第
15
题图
)15.如图,D、E分别是△ABC边AB,AC上的点,∠AED=∠B,
若AD=1,BD=AC=3,则AE的长是 .
16.某种细菌在培养过程中,每半小时分裂1次,每次一分为二,
若这种细菌由一个分裂到16个,那么这个过程要经过 分钟.
(
第17题图
)17.如图,在中,,,,
点F在边AC上,点E为边BC上的动点,将沿直线EF翻折,
点C落在点P处.若,则点P到AB距离的最小值为________.
三、解答题(一)(本大题3小题,每小题6分,共18分)
(
①
②
)18.解方程组: . .
19.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.求证:AC=EF.
20.交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门绘制出2021年五一小长假期间旅游情况统计图,根据信息解答下列问题:
(1)五一小长假期间,该市旅游景区景点共接待游客 万人,请补全条形统计图;
(2)根据2021年到该市旅游人数的情况,预计2022年五一小长假期间将有80万游客选择该市旅游,请估计有 万人会选择去E景点旅游;
(3)甲、乙两个旅行团在A、B、D三个景点中任选一个景点旅游,求两个旅行团同时选择去同一景点的概率是 .
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.2020年上半年受到新冠状肺炎疫情的影响,汽车销售行业处于不景气状态,2020年下半年合肥某汽车销售公司推行了一种新型低能耗汽车,于2020年10月份销售该型号汽车20辆,由于该型号汽车经济适用性强,销量快速上升,12月份该公司销售该型号汽车达45辆.
(1)求11月份和12月份的平均增长率;
(2)该型号汽车每辆的进价为10万元,且销售a辆汽车,汽车厂对销售公司每辆返利0.03a万元,该公司这种型号汽车的售价为11万元/辆,若使2021年1月份每辆汽车盈利不低于2.6万元,那么该公司1月份至少需要销售该型号汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
22.如图,在菱形ABCD中,对角线AC、BD相交于点M,⊙O经过点B,C,交对角线BD于点E,且,连接OE交BC于点F.
(1)试判断AB与⊙O的位置关系,并说明理由;
(2)若BD=,tan∠CBD=,求⊙O的半径.
23.如图,反比例函数(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=.
(1)求m的值;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数(x>0)的图象恰好经过DC的中点E,求直线AE的函数表达式;
(3)若直线AE与x轴交于点M,与y轴交于点N,问线段AN与线段ME的大小关系如何?请说明理由.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”;对角线相等的凸四边形叫做“对等四边形”.
(1)在“①平行四边形;②矩形;③菱形;④正方形”中一定是“十字形”的有 ;一定是“对等四边形”的有 ;(请填序号)
(2)如图1:若凸四边形ABCD是“十字形”也是“对等四边形”,F,H,G,M分别是AD,DC,AB,BC的中点,求证:四边形FGMH为正方形;
(3)如图2,在Rt△ABC中,∠B=90°,∠C=30°,AC=20,点D从点C出发沿CA方向以2个单位每秒向A匀速运动;同时点E从A出发沿AB方向以1个单位每秒向B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,DF∥AB,连接EF,是否存在时间t(秒),使得四边形ADFE为“十字形”或“对等四边形”,若存在,请求出t的值,若不存在,请说明理由.
25.如图,已知抛物线与x轴交于点A、B,与y轴交于点C,点P是抛物线上一动点,连接PB,PC.
(1)点A的坐标为 ,点B的坐标为 ;
(2)如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;
(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.
(四)(综 合)
一、选择题:
1.C 2.B 3.D 4.B 5.B 6.C 7.D 8.A 9.C 10.A
二、填空题:
11.-2 12.y(x+3)(x﹣3) 13. 14.-1 15. 16.120 17.
三、解答题(一):
18.略. .
19.∵AF∥BC, ∴∠AEB=∠EAF,
∵AB=AE, ∴∠ABC=∠AEB, ∴∠ABC=∠EAF,
∵EF⊥AE,∠BAC=90°, ∴∠BAC=∠AEF=90°,
在△ABC和△EAF中,∠BAC=∠AEF AB=AE ∠ABC=∠EAF,
∴△ABC≌△EAF, ∴AC=EF.
20.(1)50,补全条形统计图略;(2)9.6(3)
四、解答题(二):
21.(1)设11月份和12月份的平均增长率为x,
依题意得:, 解得:,(不合题意,舍去).
(2)依题意得:11-10+0.03a≥2.6, 解得:a≥53.
又∵a为整数, ∴a可取的最小值为54,
∴此时总盈利为54×(11-10+0.03×54)=141.48(万元).
22.(1)AB是⊙O的切线.
理由:连接OB, ∵OE=OB, ∴∠OEB=∠OBE,
∵四边形ABCD是菱形,AC、BD是其对角线, ∴∠ABD=∠CBD,
∵,OE是⊙O的半径, ∴OE⊥BC,
∴∠BFE=90°, ∴∠OEB+∠CBE=90°, ∴∠ABD+∠OBE=90°,
∴OB⊥AB,即AB是⊙O的切线;
(2)∵四边形ABCD是菱形,AC、BD是其对角线,BD= ∴BM=BD=,AC⊥BD,
∵tan∠CBD=, ∴CM=BM=, ∴BC=,
∵,OE是⊙O的半径, ∴BF=BC=4,
∵tan∠CBD=,OE⊥BC, ∴EF=BF=2,
设⊙O的半径为r,则OF的长为(r-2),
在Rt△OFB中,, 即,
解得:r=5, ∴⊙O的半径为5.
23.(1)∵B(2,0), ∴OB=2,
∵tan∠AOB=, ∴AB=3, ∴A(2,3),
∵反比例函数(x>0)的图象经过线段OA的端点A, ∴m=2×3=6;
(2)∵A(2,3),B(2,0), ∴线段AB的中点纵坐标为,
∵将线段AB沿x轴正方向平移到线段DC的位置, ∴线段CD的中点E的纵坐标为,
由(1)可知反比例函数解析式为,当y=时,可得,
解得x=4, ∴E(4,),
设直线AE解析式为y=kx+b, 把A、E坐标代入可得,解得,
∴直线AE的函数表达式为;
(3)相等.
理由:在,令y=0可解得x=6,令x=0可解得y=
∴M(6,0),N(0,),且A(2,3),E(4,),
∴AN=,ME=, ∴AN=ME.
五、解答题(三):
24.(1)③④,②④;
(2)如图,∵凸四边形ABCD是“十字形”也是“对等四边形”, ∴AC=BD,AC⊥BD,
∵AC⊥BD, ∴∠AEB=90°,
∵F,H,G,M分别是AD,DC,AB,BC的中点,
∴FH=AC,GM=AC,FG=BD,MH=BD,GM∥AC,FG∥BD,
∴四边形NGPE是平行四边形, ∴∠AEB=∠FGP=90°,
∵AC=BD, ∴FH=FG=GM=MH, ∴四边形FGMH菱形,
∵∠FGP=90°, ∴菱形FGMH是正方形;
(3)存在t=,使得四边形ADFE为“十字形”.
连接AF,DE, 由题意得:CD=2t,AE=t,则AD=20-2t,
Rt△ABC中,∠C=30°,∠B=90°,AC=20, ∴AB=AC=10,
∵DF∥AB, ∴∠DFC=∠B=90°, ∴DF=CD=t,
∴DF=AE, ∴四边形ADFE是平行四边形,
∵∠A=60°, ∴ADFE不可能是矩形,
当AD=DF时,ADFE是菱形,则AF⊥DE,此时ADFE是“十字形”,
∴t=20-2t, ∴t=,
∴当t=时,四边形ADFE为“十字形”.
25.(1)(-1,0),(3,0);
(2)在中, 当x=0时,y=3, ∴C(0,3).
设直线BC的解析式为y=kx+b,
将B(3,0),C(0,3)代入,得:,解得,
∴直线BC的解析式为y= -x+3,
若PE=2ED,则PD=3ED, 设P(m,),
∵PD⊥x轴于点D, ∴E(m,-m+3),
∴=3(-m+3), ∴,
解得,(舍), ∴m=2, 此时P(2,3),E(2,1),
∴PE=2, ∴. ∴△PBC的面积为3;
(3)∵△PBC是以BC为直角边的直角三角形,
∴有两种情况:
①点C为直角顶点,过点C作直线P1C⊥BC,交抛物线于点P1,交x轴于点D,连接P1B,
∵B(3,0),C(0,3), ∴OB=OC=3, ∴∠BCO=∠OBC=45°.
∵P1C⊥BC, ∴∠DCB=90°, ∴∠DCO=45°,
又∵∠DOC=90°, ∴∠ODC=45°=∠DCO, ∴OD=OC=3,
∴D(-3,0), ∴直线P1C的解析式为y=x+3,
联立,解得或(舍); ∴P1(1,4);
②点B为直角顶点,过点B作直线BP2⊥BC,交抛物线于点P2,交y轴于点E,连接P2C,
∵P1C⊥BC,BP2⊥BC, ∴P1C∥BP2,
∴设直线BP2的解析式为y=x+b,
将B(3,0)代入,得0=3+b, ∴b= -3,
∴直线BP2的解析式为y=x-3,
联立,解得或(舍), ∴P2(-2,-5).
综上,点P的坐标为(1,4)或(-2,-5).
九年级数学综合测练题 第8页 共8页
