3.7弧长及扇形的面积
图片预览





文档简介
课件26张PPT。 二中实验数学组北师大版九年级数学下册§3.7 弧长及扇形的面积第三章 圆已知⊙O的半径为R,⊙O的周长是多少?⊙O的面积是多少?温故而知新C=2πR,S⊙O=πR2
学习目标 1`掌握弧长计算公式及扇形面积的计算公式,并会应用公式解决问题 自学指导1 3`1.看课本P139的内容,掌握弧长公式。
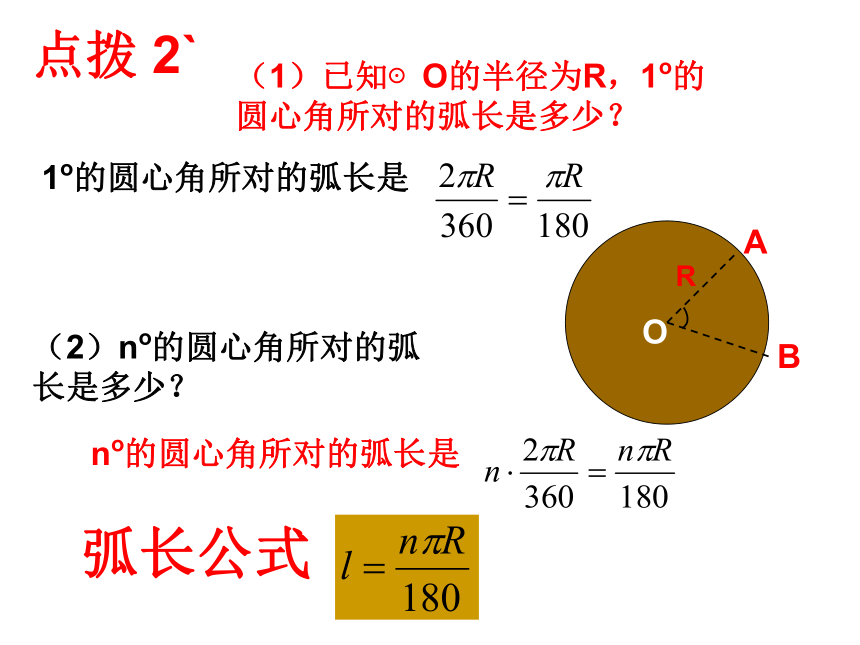
2.看例题1做P141的第2题。(1)已知⊙O的半径为R,1o的圆心角所对的弧长是多少?ABOR(2)no的圆心角所对的弧长是多少?
1o的圆心角所对的弧长是 no的圆心角所对的弧长是点拨 2`弧长公式自学检测 一: 10`
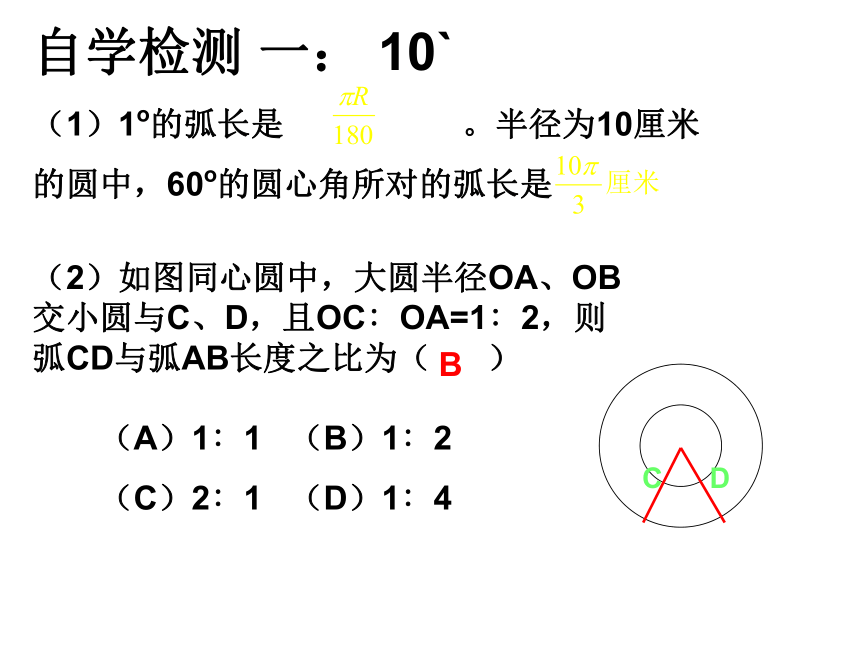
(1)1o的弧长是 。半径为10厘米
的圆中,60o的圆心角所对的弧长是(2)如图同心圆中,大圆半径OA、OB交小圆与C、D,且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )OABCD(A)1∶1 (B)1∶2
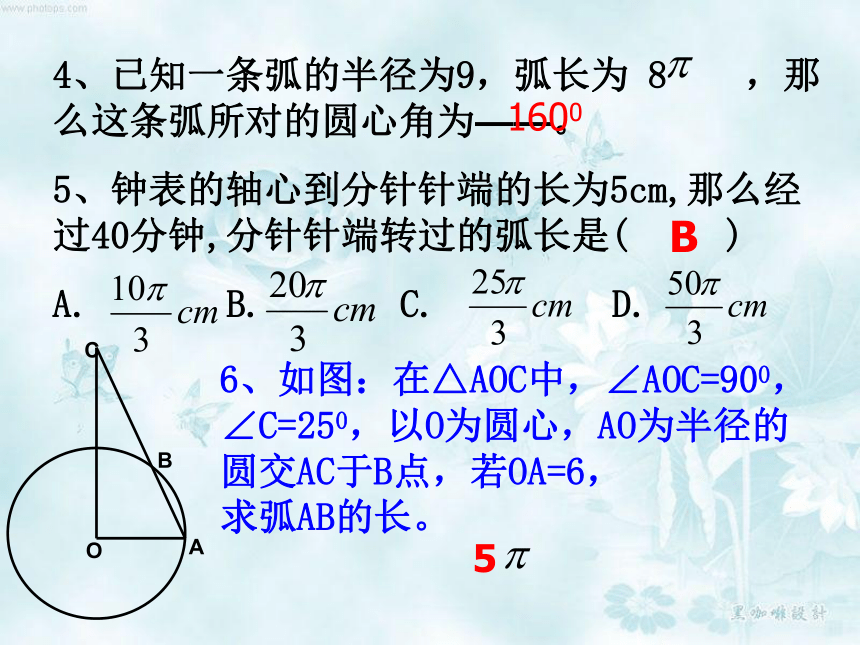
(C)2∶1 (D)1∶4B4、已知一条弧的半径为9,弧长为 8 ,那么这条弧所对的圆心角为——。
5、钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D. 6、如图:在△AOC中,∠AOC=900,
∠C=250,以O为圆心,AO为半径的
圆交AC于B点,若OA=6,
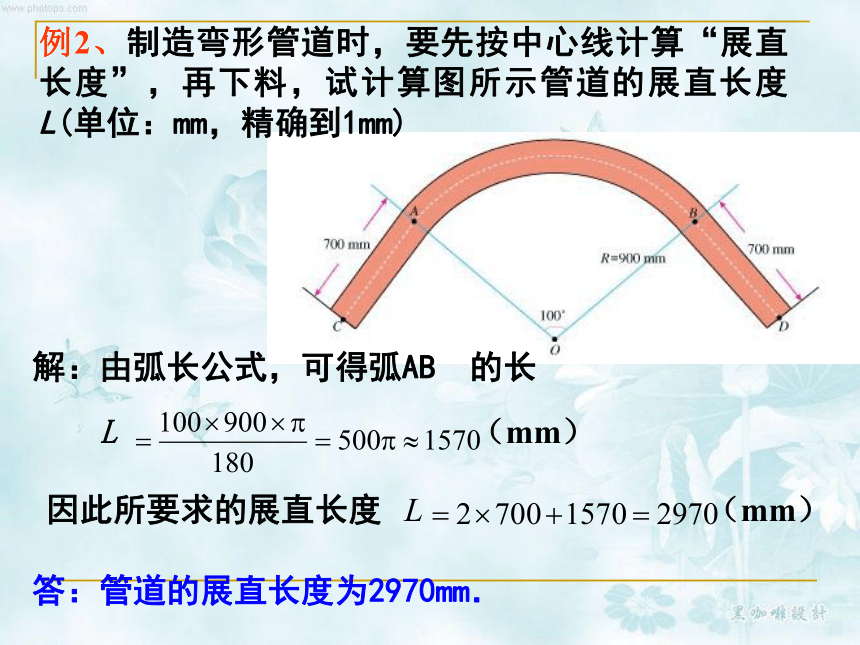
求弧AB的长。1600B5例2、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
L (mm) 因此所要求的展直长度 L (mm) 答:管道的展直长度为2970mm. 例: 如图,把Rt△ABC的斜边放在直线 上,按顺时针方向转动一次,使它转到 的位置。若BC=1,∠A=300。求点A运动到A′位置时,点A经过的路线长。变式训练:一块等边三角形的木板,边长
为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.BB1B2自学指导2 4`1.看课本P140的内容,掌握扇形面积公式。
2.看例题2做P141的第1题。弧长公式与扇形的面积公式之间的联系:(1)当已知弧长L和半径R, 求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
点拨一个扇形的圆心角为90o,半径为2,
则弧长= ,扇形面积= .2. 一个扇形的弧长为20πcm,面积是240πc㎡,则该扇形的圆心角为 .已知扇形的圆心角为120o,半径为6,则扇形的弧长是 ( )
A. 3π B.4π C.5π D.6πππ150oB自学检测二: 8` 4、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为1200,OC长为8cm,CA长为12cm,则贴纸部分的面积为( )
A. B.
C. D.A5、已知等边三角形ABC的边长为a,分别
以A、B、C为圆心,以 为半径的圆相
切于点D、E、F,
求图中阴影部分的面积S.当堂训练 10`1)扇形的圆心角为120°,弧长为6πcm,那么这个扇形的面积为 cm2.
2)面积为18π的扇形的弧长是6π,则这个扇形的半径为
3)一个扇形的弧长与面积的数值都是4,这个扇形中心角的弧度数是
4)在扇形AOB中,∠AOB=90°,弧AB的长为l,求此扇形内切圆的面积.
5)已知一扇形的周长为c(c>0),当扇形的弧长为何值时,它有最大面积?并求出面积的最大值. 5)如图,已知OPQ是半径为1,圆心角为 π/3的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积. 6)如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么,阴影部分的面积是多少平方厘米?(π取3.14) 8)如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD. (1)求证:AC=BD; (2)若图中阴影部分的面积是 3/4πcm2,OA=2cm,求OC的长. 9)有一块扇形铁板,半径为R,圆心角为60°,从这个扇形中切割下一个内接矩形,即矩形的各个顶点都在扇形的半径或弧上(如图所示),求这个内接矩形的最大面积. 10)如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5. (1)若 BD/AB= 3/5,求CD的长. (2)若∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积. (3)若将(2)中扇形卷成一个圆锥,则此圆锥的侧面积. 11)如图,在半径是2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在NQ上有一动点P,且点P到弦MN的距离为x. (1)求弦MN的长; (2)试求阴影部分面积y与x的函数关系式,并写出自变量x的取值范围; (3)试分析比较,当自变量x为何值时,阴影部分面积y与S扇形OMN的大小关系. 12)如图,OAB是一个直角扇形,分别以OA、OB为直径在扇形内部作半圆.你看,图中阴影部分像不像一条悠闲自得的大尾巴金鱼?那么这条金鱼的鱼身和鱼尾的面积哪个大些?为什么? 13)图中三角形ABD是一个等腰直角三角形,弧AB为四分之一圆弧,AD的长为4厘米,BC的长为6厘米,阴影部分的面积是多少平方厘米? 14)(2012?上海)如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E. (1)当BC=1时,求线段OD的长; (2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由; (3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
学习目标 1`掌握弧长计算公式及扇形面积的计算公式,并会应用公式解决问题 自学指导1 3`1.看课本P139的内容,掌握弧长公式。
2.看例题1做P141的第2题。(1)已知⊙O的半径为R,1o的圆心角所对的弧长是多少?ABOR(2)no的圆心角所对的弧长是多少?
1o的圆心角所对的弧长是 no的圆心角所对的弧长是点拨 2`弧长公式自学检测 一: 10`
(1)1o的弧长是 。半径为10厘米
的圆中,60o的圆心角所对的弧长是(2)如图同心圆中,大圆半径OA、OB交小圆与C、D,且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )OABCD(A)1∶1 (B)1∶2
(C)2∶1 (D)1∶4B4、已知一条弧的半径为9,弧长为 8 ,那么这条弧所对的圆心角为——。
5、钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D. 6、如图:在△AOC中,∠AOC=900,
∠C=250,以O为圆心,AO为半径的
圆交AC于B点,若OA=6,
求弧AB的长。1600B5例2、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
L (mm) 因此所要求的展直长度 L (mm) 答:管道的展直长度为2970mm. 例: 如图,把Rt△ABC的斜边放在直线 上,按顺时针方向转动一次,使它转到 的位置。若BC=1,∠A=300。求点A运动到A′位置时,点A经过的路线长。变式训练:一块等边三角形的木板,边长
为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.BB1B2自学指导2 4`1.看课本P140的内容,掌握扇形面积公式。
2.看例题2做P141的第1题。弧长公式与扇形的面积公式之间的联系:(1)当已知弧长L和半径R, 求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
点拨一个扇形的圆心角为90o,半径为2,
则弧长= ,扇形面积= .2. 一个扇形的弧长为20πcm,面积是240πc㎡,则该扇形的圆心角为 .已知扇形的圆心角为120o,半径为6,则扇形的弧长是 ( )
A. 3π B.4π C.5π D.6πππ150oB自学检测二: 8` 4、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为1200,OC长为8cm,CA长为12cm,则贴纸部分的面积为( )
A. B.
C. D.A5、已知等边三角形ABC的边长为a,分别
以A、B、C为圆心,以 为半径的圆相
切于点D、E、F,
求图中阴影部分的面积S.当堂训练 10`1)扇形的圆心角为120°,弧长为6πcm,那么这个扇形的面积为 cm2.
2)面积为18π的扇形的弧长是6π,则这个扇形的半径为
3)一个扇形的弧长与面积的数值都是4,这个扇形中心角的弧度数是
4)在扇形AOB中,∠AOB=90°,弧AB的长为l,求此扇形内切圆的面积.
5)已知一扇形的周长为c(c>0),当扇形的弧长为何值时,它有最大面积?并求出面积的最大值. 5)如图,已知OPQ是半径为1,圆心角为 π/3的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积. 6)如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么,阴影部分的面积是多少平方厘米?(π取3.14) 8)如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD. (1)求证:AC=BD; (2)若图中阴影部分的面积是 3/4πcm2,OA=2cm,求OC的长. 9)有一块扇形铁板,半径为R,圆心角为60°,从这个扇形中切割下一个内接矩形,即矩形的各个顶点都在扇形的半径或弧上(如图所示),求这个内接矩形的最大面积. 10)如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5. (1)若 BD/AB= 3/5,求CD的长. (2)若∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积. (3)若将(2)中扇形卷成一个圆锥,则此圆锥的侧面积. 11)如图,在半径是2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在NQ上有一动点P,且点P到弦MN的距离为x. (1)求弦MN的长; (2)试求阴影部分面积y与x的函数关系式,并写出自变量x的取值范围; (3)试分析比较,当自变量x为何值时,阴影部分面积y与S扇形OMN的大小关系. 12)如图,OAB是一个直角扇形,分别以OA、OB为直径在扇形内部作半圆.你看,图中阴影部分像不像一条悠闲自得的大尾巴金鱼?那么这条金鱼的鱼身和鱼尾的面积哪个大些?为什么? 13)图中三角形ABD是一个等腰直角三角形,弧AB为四分之一圆弧,AD的长为4厘米,BC的长为6厘米,阴影部分的面积是多少平方厘米? 14)(2012?上海)如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E. (1)当BC=1时,求线段OD的长; (2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由; (3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
