甘肃省天水市一中2012-2013学年高一上学期期末考试数学试题
文档属性
| 名称 | 甘肃省天水市一中2012-2013学年高一上学期期末考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 81.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-15 19:25:04 | ||
图片预览


文档简介
天水一中2012级2012-2013学年度2012级第一学期第二学段考试题
数学试题
命题:高路 审核:文贵双
一、选择题:本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.过点(1,0)且与直线x-2y-2=0平行的直线方程是( )
A. x-2y-1=0 B. x-2y+1=0 C. 2x+y-2=0 D. x+2y-1=0
2. 设,是两条不同的直线,是一个平面,则下列命题正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
3. 如图长方体中,AB=AD=2,CC1=,则二面角 C1—BD—C的大小为( )
A. 300 B. 450 C. 600 D. 900
4. 长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是( )
A. B. C. D.都不对
5.若P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程为( )
A. x+y-1=0 B.2x+y-3=0
C. x-y-3=0 D.2x-y-5=0
6.不论m为何值,直线(m-2)x-y+3m+2=0恒过定点( )
A.(3,8) B.(8,3) C.(-3,8) D.(-8,3)
7.一空间几何体的三视图如图所示,则该几何体的体积为
A. B.
C. D.
8. 正方体-中,与平面所成角的余弦值为( )
A. B. C. D.
9、点P(x,y)在直线x+y-4=0上,O是坐标原点,则│OP│的最小值是( )
A. B. C.2 D.
10、如果实数满足等式,那么的最大值是( )
A. B. C. D.
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在题中横线上.
11.过点向圆所引的切线方程为______________________
12.直线与曲线有且只有一个交点,则的取值范围是________________.__________
13.Rt△ABC的斜边在平面α内,直角顶点C是α外一点,AC、BC与α所成角分别为30°和45°.则平面ABC与α所成锐角为
14.在轴上与点和点等距离的点的坐标为 .
三、解答题(本大题共4小题,解答应写出必要的计算过程、推演步骤或文字说明)
15.(10分)
如图,在直三棱柱中,AB=1,
,BC=2.
(1)证明:;
(2)求二面角A——B的余弦值。
16. (10分)
已知ABC的顶点A,AB边上的中线CM所在直线方程为,AC边上的高BH所在直线方程为。
求:(1)顶点C的坐标;
(2)直线BC的方程.
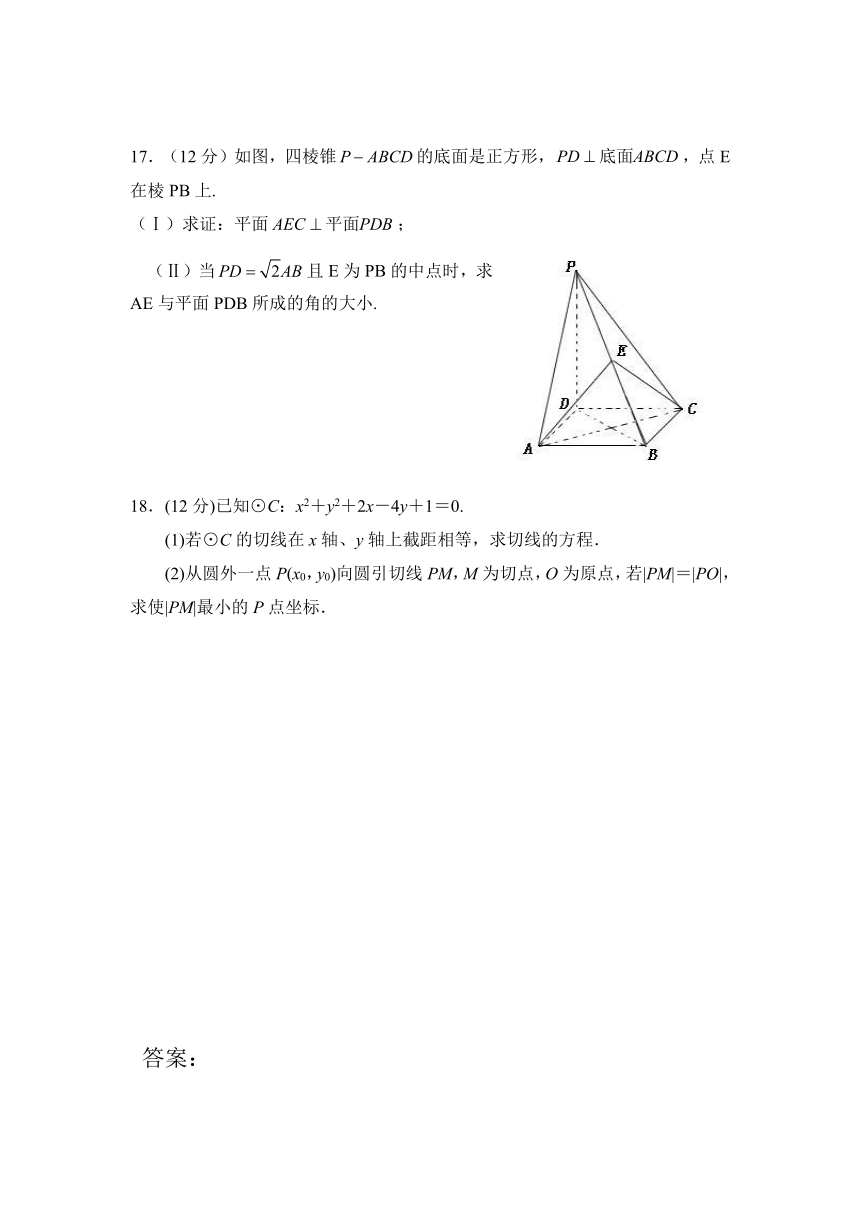
17.(12分)如图,四棱锥的底面是正方形,,点E在棱PB上.
(Ⅰ)求证:平面;
(Ⅱ)当且E为PB的中点时,求AE与平面PDB所成的角的大小.
18.(12分)已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切线在x轴、y轴上截距相等,求切线的方程.
(2)从圆外一点P(x0,y0)向圆引切线PM,M为切点,O为原点,若|PM|=|PO|,求使|PM|最小的P点坐标.
答案:
一.选择题:
1.A 2.B 3.A 4.B 5.C 6.C 7.C 8.D 9.C 10.B
二.填空题:
11. 或 12.或
13.600 14.
三.解答题:
15. (1)证明:由直棱柱的性质可得,
∴
∵在
∴ 又
∴ 又
∴
(2)解:
由已知可得
∴
由(1)可得
在等腰 在等腰
又在为所求二面角的余弦值
16.解(1)由A(1,3)及AC边上的高BH所在的直线方程
得AC所在直线方程为
又AB边上的中线CM所在直线方程为
由 得C(-1,0)
(2)法一:设B(a,b),又A(1,3) M是AB的中点 ,则M(
由已知得 得B(3,1)
又C(-1,0) 得直线BC的方程为
法二:设M(a,b), 又A(1,3) M是AB的中点,则B(2a-1,2b-3)
由已知得 得M(2,2)
∴B(3,1) 又C(-1,0) 得直线BC的方程为
17(1)略 (2)450
18. [解析] ⊙C:(x+1)2+(y-2)2=4,
圆心C(-1,2),半径r=2.
(1)若切线过原点设为y=kx,
则=2,∴k=0或.
若切线不过原点,设为x+y=a,
则=2,∴a=1±2,
∴切线方程为:y=0,y=x,
x+y=1+2和x+y=1-2.
(2)=
∴2x0-4y0+1=0,
|PM|==
∵P在⊙C外,∴(x0+1)2+(y0-2)2>4,
将x0=2y0-代入得5y-2y0+>0,
∴|PM|min=.此时P.
数学试题
命题:高路 审核:文贵双
一、选择题:本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.过点(1,0)且与直线x-2y-2=0平行的直线方程是( )
A. x-2y-1=0 B. x-2y+1=0 C. 2x+y-2=0 D. x+2y-1=0
2. 设,是两条不同的直线,是一个平面,则下列命题正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
3. 如图长方体中,AB=AD=2,CC1=,则二面角 C1—BD—C的大小为( )
A. 300 B. 450 C. 600 D. 900
4. 长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是( )
A. B. C. D.都不对
5.若P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程为( )
A. x+y-1=0 B.2x+y-3=0
C. x-y-3=0 D.2x-y-5=0
6.不论m为何值,直线(m-2)x-y+3m+2=0恒过定点( )
A.(3,8) B.(8,3) C.(-3,8) D.(-8,3)
7.一空间几何体的三视图如图所示,则该几何体的体积为
A. B.
C. D.
8. 正方体-中,与平面所成角的余弦值为( )
A. B. C. D.
9、点P(x,y)在直线x+y-4=0上,O是坐标原点,则│OP│的最小值是( )
A. B. C.2 D.
10、如果实数满足等式,那么的最大值是( )
A. B. C. D.
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在题中横线上.
11.过点向圆所引的切线方程为______________________
12.直线与曲线有且只有一个交点,则的取值范围是________________.__________
13.Rt△ABC的斜边在平面α内,直角顶点C是α外一点,AC、BC与α所成角分别为30°和45°.则平面ABC与α所成锐角为
14.在轴上与点和点等距离的点的坐标为 .
三、解答题(本大题共4小题,解答应写出必要的计算过程、推演步骤或文字说明)
15.(10分)
如图,在直三棱柱中,AB=1,
,BC=2.
(1)证明:;
(2)求二面角A——B的余弦值。
16. (10分)
已知ABC的顶点A,AB边上的中线CM所在直线方程为,AC边上的高BH所在直线方程为。
求:(1)顶点C的坐标;
(2)直线BC的方程.
17.(12分)如图,四棱锥的底面是正方形,,点E在棱PB上.
(Ⅰ)求证:平面;
(Ⅱ)当且E为PB的中点时,求AE与平面PDB所成的角的大小.
18.(12分)已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切线在x轴、y轴上截距相等,求切线的方程.
(2)从圆外一点P(x0,y0)向圆引切线PM,M为切点,O为原点,若|PM|=|PO|,求使|PM|最小的P点坐标.
答案:
一.选择题:
1.A 2.B 3.A 4.B 5.C 6.C 7.C 8.D 9.C 10.B
二.填空题:
11. 或 12.或
13.600 14.
三.解答题:
15. (1)证明:由直棱柱的性质可得,
∴
∵在
∴ 又
∴ 又
∴
(2)解:
由已知可得
∴
由(1)可得
在等腰 在等腰
又在为所求二面角的余弦值
16.解(1)由A(1,3)及AC边上的高BH所在的直线方程
得AC所在直线方程为
又AB边上的中线CM所在直线方程为
由 得C(-1,0)
(2)法一:设B(a,b),又A(1,3) M是AB的中点 ,则M(
由已知得 得B(3,1)
又C(-1,0) 得直线BC的方程为
法二:设M(a,b), 又A(1,3) M是AB的中点,则B(2a-1,2b-3)
由已知得 得M(2,2)
∴B(3,1) 又C(-1,0) 得直线BC的方程为
17(1)略 (2)450
18. [解析] ⊙C:(x+1)2+(y-2)2=4,
圆心C(-1,2),半径r=2.
(1)若切线过原点设为y=kx,
则=2,∴k=0或.
若切线不过原点,设为x+y=a,
则=2,∴a=1±2,
∴切线方程为:y=0,y=x,
x+y=1+2和x+y=1-2.
(2)=
∴2x0-4y0+1=0,
|PM|==
∵P在⊙C外,∴(x0+1)2+(y0-2)2>4,
将x0=2y0-代入得5y-2y0+>0,
∴|PM|min=.此时P.
同课章节目录
