广东省佛山市顺德区2021-2022学年九年级下学期第一次教学质量数学试题(word版无答案)
文档属性
| 名称 | 广东省佛山市顺德区2021-2022学年九年级下学期第一次教学质量数学试题(word版无答案) | 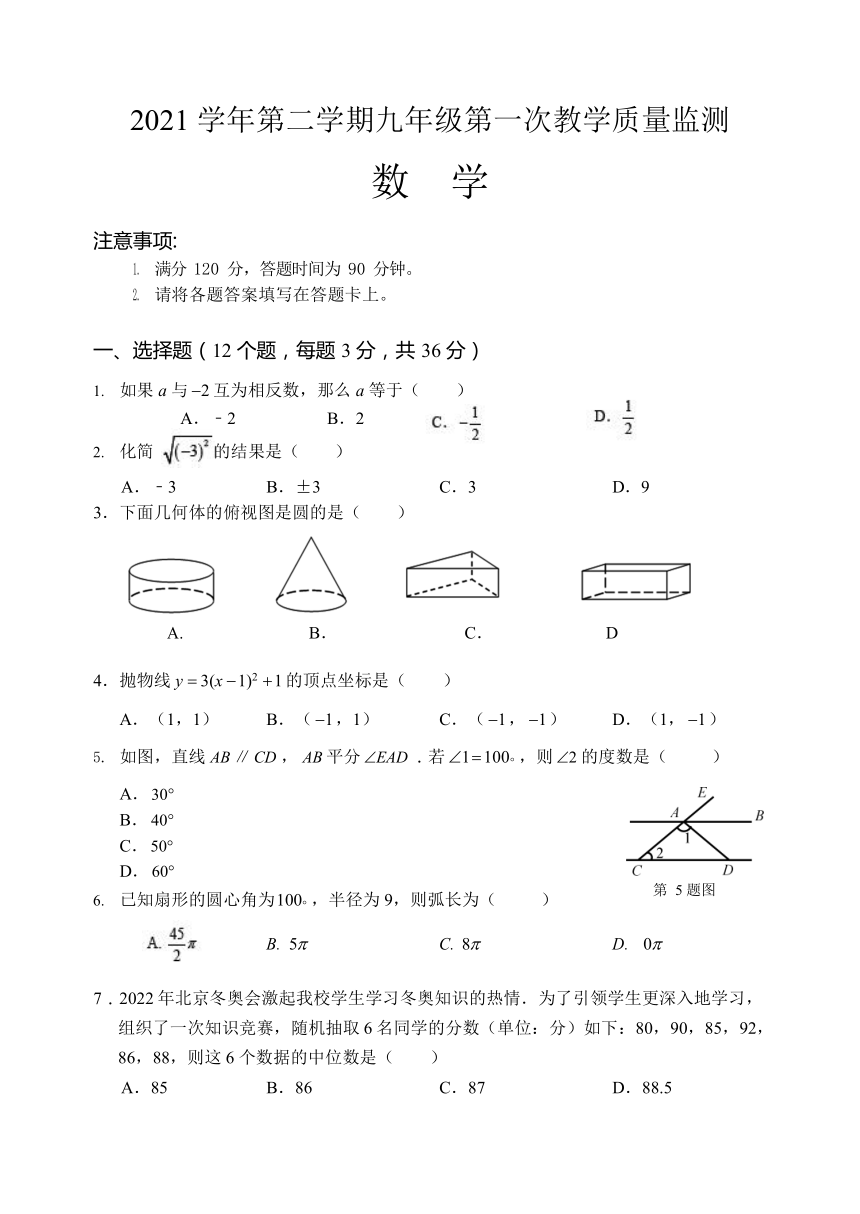 | |
| 格式 | docx | ||
| 文件大小 | 261.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 20:37:34 | ||
图片预览


文档简介
2021 学年第二学期九年级第一次教学质量监测
数 学
注意事项:
满分 120 分,答题时间为 90 分钟。
请将各题答案填写在答题卡上。
一、选择题(12 个题,每题 3 分,共 36 分)
如果 a 与2 互为相反数,那么 a 等于( )
A.﹣2 B.2
化简
的结果是( )
A.﹣3 B.±3 C.3 D.9 3.下面几何体的俯视图是圆的是( )
B. C. D
4.抛物线 y 3(x 1)2 1 的顶点坐标是( )
A.(1,1) B.( 1 ,1) C.( 1 , 1 ) D.(1, 1 )
如图,直线 AB ∥ CD , AB 平分EAD .若1 100 ,则2 的度数是( )
A. 30
B. 40
C. 50
D. 60
已知扇形的圆心角为100 ,半径为 9,则弧长为( )
第 5 题图
5
8
0
7.2022 年北京冬奥会激起我校学生学习冬奥知识的热情.为了引领学生更深入地学习, 组织了一次知识竞赛,随机抽取 6 名同学的分数(单位:分)如下:80,90,85,92, 86,88,则这 6 个数据的中位数是( )
A.85 B.86 C.87 D.88.5
如图,将正方形 ABCD 剪去 4 个全等的直角三角形(图中阴影部分),得到边长为 c
的四边形 EFGH.下列等式成立的是( )
A. a b c
B. c2 a b 2 4ab
C. c2 a b a b
D. a2 b2 c2
9.化简 的结果是()
10.如图, AB CD ,且 AB CD.E、F 是 AD 上两点,CE⊥AD,
BF⊥AD.若CE a , BF b , EF c ,则 AD 的长为( )
a b c
b c
a b c
a c
11.如图,数轴上的点 A、B 分别表示数 1、 2x 3 .则表示数x 2 的点 P 与线段 AB
的位置关系是( )
A.P 在线段 AB 上
B.P 在线段 AB 的延长线上
C.P 在线段 AB 的反向延长线上
D.不能确定
12.在△ABC 中, BAC 90° ,AB=AC,D、E 是斜边 BC 上两点, 且∠DAE=45°,将△ADC 绕点 A 顺时针旋转90° 得到△AFB, 连接 EF.下列结论:①BE⊥BF;
②△ABC 的面积等于四边形 AFBD 的面积;③当 BE CD 时,线段 DE 的长度最短.其中正确的个数是( )
第 12 题图
A.0 个 B.1 个 C.2 个 D.3 个
二、填空题(6 个题,每题 4 分,共 24 分)
13.比较大小: sin 60° tan 30° (用“>”或“<”填空).
若一个正多边形的内角是外角的 3 倍,则这个正多边形的边数为 .
把多项式 a3 9a 分解因式 .
如图, 为了测量操场上一棵大树的高度, 小明拿来一面镜子平放在离树根部 5m 的地面上,然后沿着树根和镜子所在的直线后退,当后退 1m 时,正好在镜中看见树的顶端.若小明的眼睛到地面的距离为 1.5m,则大树的高度是 m.
两个全等矩形纸条的长与宽分别为 8 和 6.若按图所示交叉叠放在一起,则重合部分构成的四边形周长为 .
第 16 题图
第 17 题图
18.二次函数 y ax2 2ax c ( a 0 )的图象过 A( 3 , y1 ),B( 1 , y2 ),
C(2, y3 ),D(4, y4 )四个点.(1) y3 = (用关于 a 或 c 的代数
式表示);(2)若 y4 y2 0 时,则 y3 y1 0 .(填“>”、“<”或“=”)
三、解答题(6 个题,共 60 分)
19.(本题满分 8 分)已知不等式组
(1)解上述不等式组;
(2)从(1)的结果中选择一个整数是方程 的解,求m的值.
20.(本题满分 8 分)如图,A,B,C,D 是⊙O 上的四个点, ADB BDC 60 ,过点 A 作 AE // BC 交 CD 延长线于点 E.
求∠ ABC 的大小;
证明:AE 是⊙O 的切线.
(
型号
价格
A
型
200
元
/
只
B
型
240
元
/
只
)21.(本题满分 10 分)为落实“垃圾分类回收,科学处理”的政策,某花园小区购买 A、B 两种型号的垃圾分类回收箱 20 只进行垃圾分类投放,共支付费用 4320 元.A、B 型号价格信息如表:
请问小区购买 A 型和 B 型垃圾回收箱各多少只?
因受到居民欢迎,准备再次购进 A、B 两种型号的垃圾分类回收箱共 40 只,其中 A 类的数量不大于 B 类的数量的 2 倍.求购买多少只 A 类回收箱支出的费用最少,最少费用是多少元?
(
1
)22.(本题满分 10 分)抛物线C : y ax2 4a 1x a 5 (a 0) .
将C1 先向右平移 m 个单位,再向下平移 n 个单位得到C2 ,点 A(3, 4 n )和点 B(4, 6 2n )在C2 上.当C1 的对称轴为 y 轴时,求C2 的表达式;
求证:不论 a 为何值,抛物线C1 与 x 轴总有公共点.
23.(本题满分 12 分)如图,∠MON=90°,点 A,B 分别在射线 OM,ON 上(不与点 O 重合),且OA OB ,OP 平分∠MON,线段 AB 的垂直平分线分别与 OP,AB,OM 交于点 C,D,E,连接 CB,在射线 ON 上取点 F,使得OF OA ,连接 CF.
用尺规作图法依题意补全图形;
求证:CB=CF;
写出线段 CF 与 AB 之间的数量关系,并证明.
24.(本题满分 12 分)如图,点 O 是平面直角坐标系的原点,P 是反比例函数
( k 0 , x 0 )图象上的动点,以 P 为圆心,PO 为半径的圆与 x、y 轴分别交于点
A,B,连接 AB.
求△OAB 的面积;
当 k 4 时,求线段 AB 的最小值;
在(2)的条件下,点 C 是反比例函数图象上的一点(不与点 P 重合),连接
PC,AC.当ACP 是直角时,求点 C 横坐标的近似值(结果保留一位小数).
备用图
数 学
注意事项:
满分 120 分,答题时间为 90 分钟。
请将各题答案填写在答题卡上。
一、选择题(12 个题,每题 3 分,共 36 分)
如果 a 与2 互为相反数,那么 a 等于( )
A.﹣2 B.2
化简
的结果是( )
A.﹣3 B.±3 C.3 D.9 3.下面几何体的俯视图是圆的是( )
B. C. D
4.抛物线 y 3(x 1)2 1 的顶点坐标是( )
A.(1,1) B.( 1 ,1) C.( 1 , 1 ) D.(1, 1 )
如图,直线 AB ∥ CD , AB 平分EAD .若1 100 ,则2 的度数是( )
A. 30
B. 40
C. 50
D. 60
已知扇形的圆心角为100 ,半径为 9,则弧长为( )
第 5 题图
5
8
0
7.2022 年北京冬奥会激起我校学生学习冬奥知识的热情.为了引领学生更深入地学习, 组织了一次知识竞赛,随机抽取 6 名同学的分数(单位:分)如下:80,90,85,92, 86,88,则这 6 个数据的中位数是( )
A.85 B.86 C.87 D.88.5
如图,将正方形 ABCD 剪去 4 个全等的直角三角形(图中阴影部分),得到边长为 c
的四边形 EFGH.下列等式成立的是( )
A. a b c
B. c2 a b 2 4ab
C. c2 a b a b
D. a2 b2 c2
9.化简 的结果是()
10.如图, AB CD ,且 AB CD.E、F 是 AD 上两点,CE⊥AD,
BF⊥AD.若CE a , BF b , EF c ,则 AD 的长为( )
a b c
b c
a b c
a c
11.如图,数轴上的点 A、B 分别表示数 1、 2x 3 .则表示数x 2 的点 P 与线段 AB
的位置关系是( )
A.P 在线段 AB 上
B.P 在线段 AB 的延长线上
C.P 在线段 AB 的反向延长线上
D.不能确定
12.在△ABC 中, BAC 90° ,AB=AC,D、E 是斜边 BC 上两点, 且∠DAE=45°,将△ADC 绕点 A 顺时针旋转90° 得到△AFB, 连接 EF.下列结论:①BE⊥BF;
②△ABC 的面积等于四边形 AFBD 的面积;③当 BE CD 时,线段 DE 的长度最短.其中正确的个数是( )
第 12 题图
A.0 个 B.1 个 C.2 个 D.3 个
二、填空题(6 个题,每题 4 分,共 24 分)
13.比较大小: sin 60° tan 30° (用“>”或“<”填空).
若一个正多边形的内角是外角的 3 倍,则这个正多边形的边数为 .
把多项式 a3 9a 分解因式 .
如图, 为了测量操场上一棵大树的高度, 小明拿来一面镜子平放在离树根部 5m 的地面上,然后沿着树根和镜子所在的直线后退,当后退 1m 时,正好在镜中看见树的顶端.若小明的眼睛到地面的距离为 1.5m,则大树的高度是 m.
两个全等矩形纸条的长与宽分别为 8 和 6.若按图所示交叉叠放在一起,则重合部分构成的四边形周长为 .
第 16 题图
第 17 题图
18.二次函数 y ax2 2ax c ( a 0 )的图象过 A( 3 , y1 ),B( 1 , y2 ),
C(2, y3 ),D(4, y4 )四个点.(1) y3 = (用关于 a 或 c 的代数
式表示);(2)若 y4 y2 0 时,则 y3 y1 0 .(填“>”、“<”或“=”)
三、解答题(6 个题,共 60 分)
19.(本题满分 8 分)已知不等式组
(1)解上述不等式组;
(2)从(1)的结果中选择一个整数是方程 的解,求m的值.
20.(本题满分 8 分)如图,A,B,C,D 是⊙O 上的四个点, ADB BDC 60 ,过点 A 作 AE // BC 交 CD 延长线于点 E.
求∠ ABC 的大小;
证明:AE 是⊙O 的切线.
(
型号
价格
A
型
200
元
/
只
B
型
240
元
/
只
)21.(本题满分 10 分)为落实“垃圾分类回收,科学处理”的政策,某花园小区购买 A、B 两种型号的垃圾分类回收箱 20 只进行垃圾分类投放,共支付费用 4320 元.A、B 型号价格信息如表:
请问小区购买 A 型和 B 型垃圾回收箱各多少只?
因受到居民欢迎,准备再次购进 A、B 两种型号的垃圾分类回收箱共 40 只,其中 A 类的数量不大于 B 类的数量的 2 倍.求购买多少只 A 类回收箱支出的费用最少,最少费用是多少元?
(
1
)22.(本题满分 10 分)抛物线C : y ax2 4a 1x a 5 (a 0) .
将C1 先向右平移 m 个单位,再向下平移 n 个单位得到C2 ,点 A(3, 4 n )和点 B(4, 6 2n )在C2 上.当C1 的对称轴为 y 轴时,求C2 的表达式;
求证:不论 a 为何值,抛物线C1 与 x 轴总有公共点.
23.(本题满分 12 分)如图,∠MON=90°,点 A,B 分别在射线 OM,ON 上(不与点 O 重合),且OA OB ,OP 平分∠MON,线段 AB 的垂直平分线分别与 OP,AB,OM 交于点 C,D,E,连接 CB,在射线 ON 上取点 F,使得OF OA ,连接 CF.
用尺规作图法依题意补全图形;
求证:CB=CF;
写出线段 CF 与 AB 之间的数量关系,并证明.
24.(本题满分 12 分)如图,点 O 是平面直角坐标系的原点,P 是反比例函数
( k 0 , x 0 )图象上的动点,以 P 为圆心,PO 为半径的圆与 x、y 轴分别交于点
A,B,连接 AB.
求△OAB 的面积;
当 k 4 时,求线段 AB 的最小值;
在(2)的条件下,点 C 是反比例函数图象上的一点(不与点 P 重合),连接
PC,AC.当ACP 是直角时,求点 C 横坐标的近似值(结果保留一位小数).
备用图
同课章节目录
