贵州省湄潭中学2012-2013学年高一上学期期末考试 数学试题
文档属性
| 名称 | 贵州省湄潭中学2012-2013学年高一上学期期末考试 数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-21 12:47:36 | ||
图片预览



文档简介
湄潭中学2012—2013学年第一学期学期测试
高一年级数学科试卷
命题人:李郧钟
第一部分 选择题(共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.
1.设集合,那么集合是( )
A. B. C. D.
2. 设集合和集合都是自然数集,映射把集合中的元素映射到集合中的元素,则在映射下,像20的原像是( )
A. 2 B. 3 C.4 D. 5
3. 与函数有相同的图像的函数是( )
A. B.
C. D.
4. 已知,那么=( )
A.4 B.16 C. D.
5. 下列函数中既是奇函数,又是其定义域上的增函数的是( )
A. B. C. D.
6. 已知函数,则此函数的值域为( )
A. B. C. D.
7.已知函数的图像是连续不断的,有如下的对应值表:
1
2
3
4
5
6
7
123.5
21.5
-7.82
11.57
-53.7
-26.7
-29.6
那么函数在区间上的零点至少有( )
A. 2个 B. 3个 C. 4个 D. 5个
8.设,,,则 ( )
A. B. C. D.
9. 设是上的奇函数,且,当时,,
则等于( )
A. B. C. D.
10. 如果直线,那么的位置关系是( )
A. 相交 B. C. D. 或
11. 一个圆柱的侧面展开图是正方形,这个圆柱的表面积与侧面积之比是( )
A. B. C. D.
12. 下列四个结论:
⑴两条直线都和同一个平面平行,则这两条直线平行。
⑵两条直线没有公共点,则这两条直线平行。
⑶两条直线都和第三条直线垂直,则这两条直线平行。
⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行。
其中正确的个数为( )
A.0 B. C. D.
第二部分 非选择题(共90分)
二、填空题:本大题共4小题, 每小题5分,共20分
13. 幂函数的图象过点,则的解析式为_______________
14. 已知函数分别由下表给出,则_______,________.
1
2
3
4
1
2
3
4
2
3
4
1
2
1
4
3
15. 正方体的表面积与其内切球表面积的比为 .
16.函数是定义在R上的奇函数,并且当时,,那么,= .
三、解答题:本大题共6小题,共70分.解答应写出文字说明、演算步骤或推证过程.(其中第15题10分,其他每题12分)
17已知集合,,.
(1) 求,;
(2) 若,求a的取值范围.
18.已知函数.
(1)判断的奇偶性,并证明你的结论;
(2)证明:函数在内是增函数.
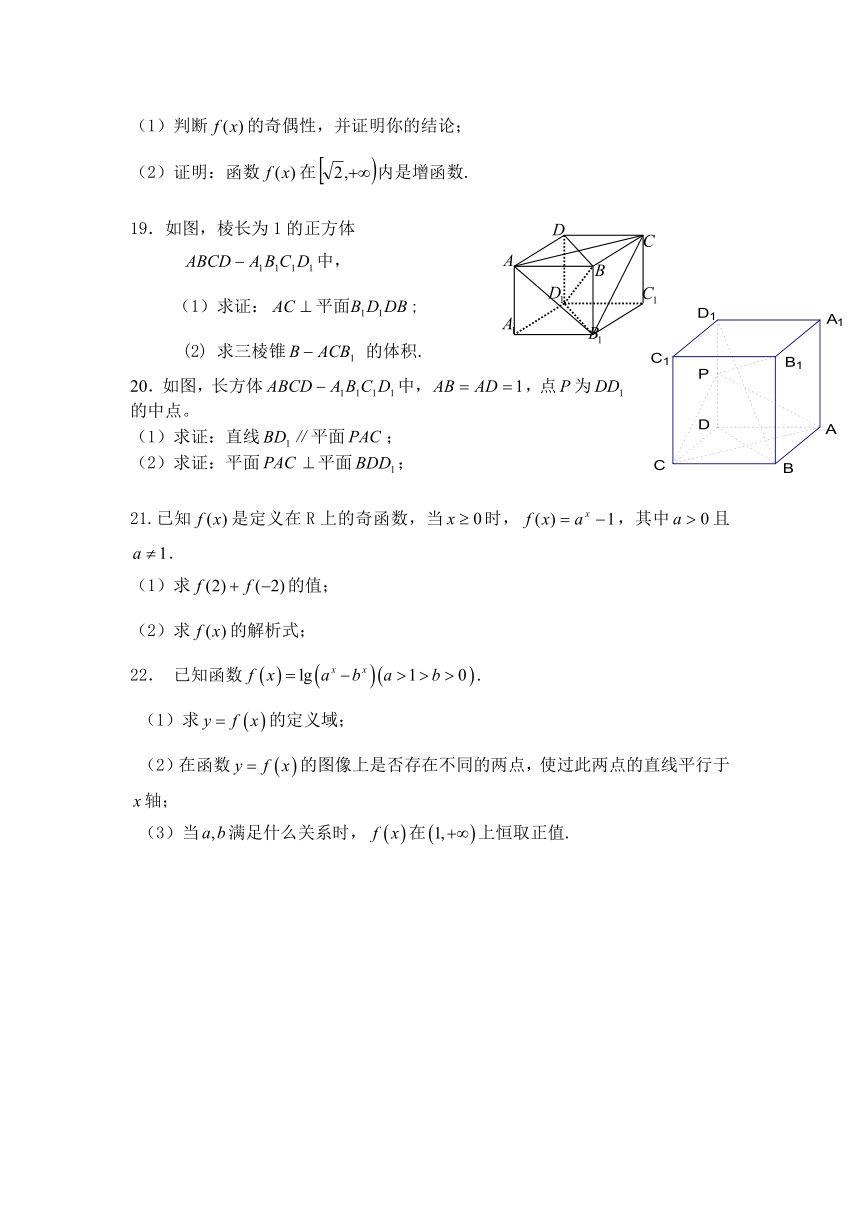
19.如图,棱长为1的正方体
中,
(1)求证:;
(2) 求三棱锥 的体积.
20.如图,长方体中,,点为的中点。
(1)求证:直线∥平面;
(2)求证:平面平面;
21.已知是定义在R上的奇函数,当时,,其中且.
(1)求的值;
(2)求的解析式;
22. 已知函数.
(1)求的定义域;
(2)在函数的图像上是否存在不同的两点,使过此两点的直线平行于轴;
(3)当满足什么关系时,在上恒取正值.
湄潭中学2012—2013学年第一学期学期测试
高一年级数学科试卷
第Ⅱ卷答题卡
一.选择题(60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二.填空题(20分)
13.
14.
15.
16.
三.解答题(70分)
17.(10分)已知集合,,.
(1) 求,;
(2) 若,求a的取值范围.
18.(12分)已知函数.
(1)判断的奇偶性,并证明你的结论;
(2)证明:函数在内是增函数.
19.(12分)如图,棱长为1的正方体中,
(1)求证:;
(2) 求三棱锥 的体积
20.(12分)如图,长方体中,,点为的中点。
(1)求证:直线∥平面;
(2)求证:平面平面;
21.(12分)已知是定义在R上的奇函数,当时,,其中且.
(1)求的值;
(2)求的解析式;
22.(12分) 已知函数.
(1)求的定义域;
(2)在函数的图像上是否存在不同的两点,使过此两点的直线平行于轴;
(3)当满足什么关系时,在上恒取正值.
湄潭中学2012—2013学年第一学期学期测试高一年级数学科试卷
参考答案及评分标准
一、选择题:本大题主要考查基本知识和基本运算. 共12小题,每小题5分,满分6 0分.
1—12 CCDBC DBABD AA
二、填空题:本大题主要考查基本知识和基本运算. 共4小题,每小题5分,满分2 0分.
13.
14. 2 3
15. 6:∏
16. -2
三、解答题:
第17题
解: , (2分)
,
(5分)
(2)由(1)知,
①当时,满足,此时,得; (7分)
②当时,要,则,解得; (10分)
第18题
解:(1)函数的定义域是 (1分)
是奇函数 (5分)
(2)设,且 (6分)
则 (7分)
(9分)
, (10分)
(11分)
故在内是增函数 (12分)
第19题
(1)证明: (3分)
在正方形中,, (5分)
(6分)
(2)解: (2) (12分)
第20题
证明:(1)设AC和BD交于点O,连PO,
由P,O分别是,BD的中点,
故PO//,
所以直线∥平面 (6分)
(2)长方体中,,
底面ABCD是正方形,则ACBD
又面ABCD,则AC,
所以AC面,则平面平面 (12分)
第21题
解:(1)因是奇函数,所以有,所以=0. (6分)
(2)当时,
(8分)
由是奇函数有,,
(10分)
(12分)
第22题
解:(1)由得, (2分)
由已知,故, (3分)
即函数的定义域为. (4分)
(2)设
则. (5分)
故,
即.在上为增函数. (6分)
假设函数的图像上存在不同的两点,使直线平行于轴,即,这与是增函数矛盾.故函数的图像上不存在不同的两点,使过这两点的直线平行于轴. (8分)
(3)由(2)知,在是增函数,
在上也是增函数. (9分)
当时,. (10分)
只需,即,即, (11分)
时,在上恒取正值. (12分)
高一年级数学科试卷
命题人:李郧钟
第一部分 选择题(共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.
1.设集合,那么集合是( )
A. B. C. D.
2. 设集合和集合都是自然数集,映射把集合中的元素映射到集合中的元素,则在映射下,像20的原像是( )
A. 2 B. 3 C.4 D. 5
3. 与函数有相同的图像的函数是( )
A. B.
C. D.
4. 已知,那么=( )
A.4 B.16 C. D.
5. 下列函数中既是奇函数,又是其定义域上的增函数的是( )
A. B. C. D.
6. 已知函数,则此函数的值域为( )
A. B. C. D.
7.已知函数的图像是连续不断的,有如下的对应值表:
1
2
3
4
5
6
7
123.5
21.5
-7.82
11.57
-53.7
-26.7
-29.6
那么函数在区间上的零点至少有( )
A. 2个 B. 3个 C. 4个 D. 5个
8.设,,,则 ( )
A. B. C. D.
9. 设是上的奇函数,且,当时,,
则等于( )
A. B. C. D.
10. 如果直线,那么的位置关系是( )
A. 相交 B. C. D. 或
11. 一个圆柱的侧面展开图是正方形,这个圆柱的表面积与侧面积之比是( )
A. B. C. D.
12. 下列四个结论:
⑴两条直线都和同一个平面平行,则这两条直线平行。
⑵两条直线没有公共点,则这两条直线平行。
⑶两条直线都和第三条直线垂直,则这两条直线平行。
⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行。
其中正确的个数为( )
A.0 B. C. D.
第二部分 非选择题(共90分)
二、填空题:本大题共4小题, 每小题5分,共20分
13. 幂函数的图象过点,则的解析式为_______________
14. 已知函数分别由下表给出,则_______,________.
1
2
3
4
1
2
3
4
2
3
4
1
2
1
4
3
15. 正方体的表面积与其内切球表面积的比为 .
16.函数是定义在R上的奇函数,并且当时,,那么,= .
三、解答题:本大题共6小题,共70分.解答应写出文字说明、演算步骤或推证过程.(其中第15题10分,其他每题12分)
17已知集合,,.
(1) 求,;
(2) 若,求a的取值范围.
18.已知函数.
(1)判断的奇偶性,并证明你的结论;
(2)证明:函数在内是增函数.
19.如图,棱长为1的正方体
中,
(1)求证:;
(2) 求三棱锥 的体积.
20.如图,长方体中,,点为的中点。
(1)求证:直线∥平面;
(2)求证:平面平面;
21.已知是定义在R上的奇函数,当时,,其中且.
(1)求的值;
(2)求的解析式;
22. 已知函数.
(1)求的定义域;
(2)在函数的图像上是否存在不同的两点,使过此两点的直线平行于轴;
(3)当满足什么关系时,在上恒取正值.
湄潭中学2012—2013学年第一学期学期测试
高一年级数学科试卷
第Ⅱ卷答题卡
一.选择题(60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二.填空题(20分)
13.
14.
15.
16.
三.解答题(70分)
17.(10分)已知集合,,.
(1) 求,;
(2) 若,求a的取值范围.
18.(12分)已知函数.
(1)判断的奇偶性,并证明你的结论;
(2)证明:函数在内是增函数.
19.(12分)如图,棱长为1的正方体中,
(1)求证:;
(2) 求三棱锥 的体积
20.(12分)如图,长方体中,,点为的中点。
(1)求证:直线∥平面;
(2)求证:平面平面;
21.(12分)已知是定义在R上的奇函数,当时,,其中且.
(1)求的值;
(2)求的解析式;
22.(12分) 已知函数.
(1)求的定义域;
(2)在函数的图像上是否存在不同的两点,使过此两点的直线平行于轴;
(3)当满足什么关系时,在上恒取正值.
湄潭中学2012—2013学年第一学期学期测试高一年级数学科试卷
参考答案及评分标准
一、选择题:本大题主要考查基本知识和基本运算. 共12小题,每小题5分,满分6 0分.
1—12 CCDBC DBABD AA
二、填空题:本大题主要考查基本知识和基本运算. 共4小题,每小题5分,满分2 0分.
13.
14. 2 3
15. 6:∏
16. -2
三、解答题:
第17题
解: , (2分)
,
(5分)
(2)由(1)知,
①当时,满足,此时,得; (7分)
②当时,要,则,解得; (10分)
第18题
解:(1)函数的定义域是 (1分)
是奇函数 (5分)
(2)设,且 (6分)
则 (7分)
(9分)
, (10分)
(11分)
故在内是增函数 (12分)
第19题
(1)证明: (3分)
在正方形中,, (5分)
(6分)
(2)解: (2) (12分)
第20题
证明:(1)设AC和BD交于点O,连PO,
由P,O分别是,BD的中点,
故PO//,
所以直线∥平面 (6分)
(2)长方体中,,
底面ABCD是正方形,则ACBD
又面ABCD,则AC,
所以AC面,则平面平面 (12分)
第21题
解:(1)因是奇函数,所以有,所以=0. (6分)
(2)当时,
(8分)
由是奇函数有,,
(10分)
(12分)
第22题
解:(1)由得, (2分)
由已知,故, (3分)
即函数的定义域为. (4分)
(2)设
则. (5分)
故,
即.在上为增函数. (6分)
假设函数的图像上存在不同的两点,使直线平行于轴,即,这与是增函数矛盾.故函数的图像上不存在不同的两点,使过这两点的直线平行于轴. (8分)
(3)由(2)知,在是增函数,
在上也是增函数. (9分)
当时,. (10分)
只需,即,即, (11分)
时,在上恒取正值. (12分)
同课章节目录
