重庆市万盛经济技术开发区溱州中学2021-2022学年九年级下学期开学考试数学试题(Word版,无答案)
文档属性
| 名称 | 重庆市万盛经济技术开发区溱州中学2021-2022学年九年级下学期开学考试数学试题(Word版,无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 23:37:21 | ||
图片预览



文档简介
溱州中学教育集团2021-2022学年度下期九年级规范化训练(一)
数学试题
一、选择题:(本大题12个小题,每小题4分,共48分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将答题卡上对应题目的正确答案标号涂黑.
1.﹣8的绝对值是( )
A.﹣8 B.8 C.﹣ D.
2.下列新能源汽车的标志,是中心对称图形的是( )
A.B.C.D.
下列计算,正确的是( )
A.a2 a3=a6 B.5a﹣3a=2 C.a6÷a2=a4 D.(a2)3=a5
4.如图,△ABC与△DEF位似,点O为位似中心,已知BO:OE=2:1,则△ABC与△DEF的面积比是( )
A.9:1 B.4:1 C.3:1 D.2:1
5 . 如图,△ADC内接于⊙O,BC是⊙O的直径,若∠A=66°,则∠BCD等于( )
A.14° B.24° C.34° D.66°
估计×+的运算结果应在哪两个连续自然数之间( )
A.2和3 B.3和4 C.4和5 D.5和6
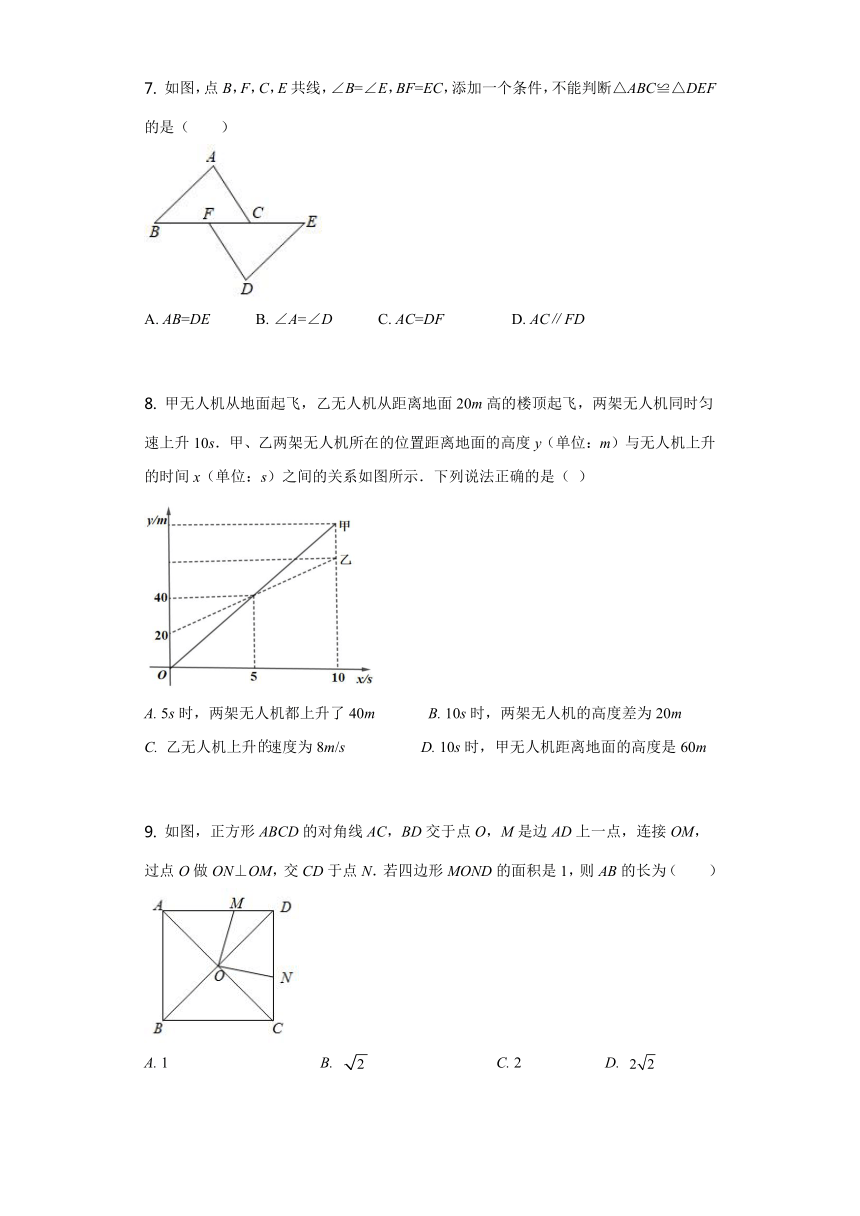
7. 如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A. AB=DE B. ∠A=∠D C. AC=DF D. AC∥FD
8. 甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )
A. 5s时,两架无人机都上升了40m B. 10s时,两架无人机的高度差为20m
C. 乙无人机上升速度为8m/s D. 10s时,甲无人机距离地面的高度是60m
9. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O做ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A. 1 B. C. 2 D.
10.《九章算术》中有这样一个题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别放在一起而且用称称重,5只雀总重量比6只燕的总重量要重、若交换一只雀、一只燕,它们重量相等,5只雀,6只燕重量为1斤.问每1只雀、燕各重多少斤?”设每一只雀的重量为x斤,每一只燕的重量为y斤,则可建立方程组为( )
A. B.
C. D.
11若整数a使关于x的分式方程+=1的解为正整数,且使关于y的不等式组有解,则满足条件的整数a的值之积是( )
A.﹣4 B.0 C.16 D.64
二次函数 图象如图,下列结论:
① ;②若
③ ;当 时, 其中正确的有( )
B
C. D.
二、填空题:(本大题4个小题,每小题4分,共16分)请将每小题的答案直接填在答题卡中对应的横线上
13. 3﹣1+(3﹣π)0=___________.
14. 在学校开设的数学学科校本课程学习中,张敏和黎明分别在《数学与生活》《数学与天文》《数学与实验》中随机选择一门,两人恰好选中同一门课程的概率为__________.
15. 在平行四边形ABCD中,P为AB上一点,BP=3,BC=3,∠A=60°,以B为圆心,BP为半径画弧与CD交于点E,并刚好经过C点,则阴影部分面积为__________(结果保留π).
金鹏手机专卖店以相同的价格购进A、B两种手机,并将A、B两种手机分别按利润率50%和80%定价销售.一段时间后,分别售出各自总进货量的30%和50%,此时,A、B两种手机的营业额之比为3:5.为迎接店庆十周年,商店决定将B种手机降价销售,A种手机价格不变,最终全部售完,已知A、B两种手机的总利润之比为20:21,则B种手机在降价销售时的利润率为_________.
三、解答题:(本大题8个小题,共76分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上
17.化简:
(1)(x+y)(x﹣y)+(x﹣2y)2; (2)(1﹣)÷.
18.如图,山顶上有一个信号塔AC,已知信号塔高AC=15米,在山脚下点B处测得塔底C的仰角∠CBD=36.9°,塔顶A的仰角∠ABD=42.0°,求山高CD(点A,C,D在同一条竖直线上).
(参考数据:tan36.9°≈0.75,sin36.9°≈0.60,tan42.0°≈0.90.)
19. 在四边形ABCD中,∠B=90°,AD∥BC,AD=CD.
(1)用尺规作∠ADC的平分线(基本作图,保留作图痕迹,不写作法);
(2)在(1)的情形下,设∠ADC的平分线交BC于点F,连接AF,猜想四边形AFCD是哪种特殊的平行四边形?并证明你的猜想.
20.钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据:
甲小区:
乙小区:
整理数据:
成绩(分)
甲小区
乙小区
分析数据:
统计量 平均数 中位数 众数
甲小区
乙小区
应用数据:
(1)填空:________,________,________,________;
(2)若甲小区共有人参与答卷,请估计甲小区成绩大于分的人数;
(3)根据以上数据,________(填“甲”或“乙”)小区对新型冠状病毒肺炎防护知识掌握得更好,理由____________________________________________________________________
21.如图,已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2),一次函数的图象交x轴于点C.
(1)求这两个函数的关系式;
(2)求△AOB的面积;
(3)结合图象直接写出y1>y2时,x的取值范围.
22.为响应国家号召,帮助农副产品走出大山,“村头”电商平台将咸蛋和豆腐乳进行网上销售.咸蛋售价为4元/袋,豆腐乳售价为5元/袋,5月份咸蛋的销量比豆腐乳的销量多1200袋,五月份咸蛋的总销售额为豆腐乳总销售额的两倍.
(1)5月份咸蛋和豆腐乳的销售量分别为多少袋?
(2)6月份咸蛋售价比5月份降低了a%,销量比5月份增加了a%.豆腐乳的销量比5月份增加了a%,售价保持不变,结果咸蛋和豆腐乳6月份的总销售额比5月份增加a%,求a的值.
23.阅读下列材料,解决问题.
【材料1】对于任意一个多位数,如果它的各位数字之和除以一个正整数n所得的余数与它自身除以这个正整数n所得的余数相同,我们就称这个多位数是n的“余同数”.例如:对于多位数2714,2714÷3=904…2,且(2+7+1+4)÷3=4…2,则2714是3的“余同数”.
【材料2】对于任意两个多位数A,B,若A除以正整数n所得的余数与B除以正整数n所得的余数相同,则A与B的差一定能被n整除.
(1)判断3142是否是5的“余同数”,并说明理由;
(2)若一个三位数是7的“余同数”,它的百位数字与十位数字之和小于9,个位数字比百位数字大1,求所有符合条件的三位数.
24.如图1所示,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A和B两点,与y轴交于点C;直线y=x+3经过点A,C.
(1)求抛物线的函数表达式;
(2)点P是抛物线上位于第二象限的一个动点,求四边形ABCP面积的最大值及此时点P的坐标;
(3)如图2,将原抛物线向射线AC方向平移2个单位长度得到抛物线y1,点N为y轴上一动点,抛物线y1上是否存在点M,使以点A,B,N,M为顶点的四边形为平行四边形,若存在,请直接写出点N的坐标;若不存在,请说明理由.
四、解答题:(本大题1个小题,共10分)解答时必须给出必要的演算过程或推理步骤
25.在△ABC中,∠ABC=90°,AB=BC,以点A为旋转中心,将边AC逆时针旋转一定角度,得到线段AD,使BD∥AC,AD交BC于点G,过点C作CE⊥AD交AD于点F.
(1)若AB=3,求BD的长;
(2)求证:AG=CF+DF;
(3)点M是AC边上一动点,在线段BM上存在一点N,使NB+NA+NC的值最小时,NB的长为m,请直接用含m的式子表示NB+NA+NC的最小值.
数学试题
一、选择题:(本大题12个小题,每小题4分,共48分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将答题卡上对应题目的正确答案标号涂黑.
1.﹣8的绝对值是( )
A.﹣8 B.8 C.﹣ D.
2.下列新能源汽车的标志,是中心对称图形的是( )
A.B.C.D.
下列计算,正确的是( )
A.a2 a3=a6 B.5a﹣3a=2 C.a6÷a2=a4 D.(a2)3=a5
4.如图,△ABC与△DEF位似,点O为位似中心,已知BO:OE=2:1,则△ABC与△DEF的面积比是( )
A.9:1 B.4:1 C.3:1 D.2:1
5 . 如图,△ADC内接于⊙O,BC是⊙O的直径,若∠A=66°,则∠BCD等于( )
A.14° B.24° C.34° D.66°
估计×+的运算结果应在哪两个连续自然数之间( )
A.2和3 B.3和4 C.4和5 D.5和6
7. 如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A. AB=DE B. ∠A=∠D C. AC=DF D. AC∥FD
8. 甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )
A. 5s时,两架无人机都上升了40m B. 10s时,两架无人机的高度差为20m
C. 乙无人机上升速度为8m/s D. 10s时,甲无人机距离地面的高度是60m
9. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O做ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A. 1 B. C. 2 D.
10.《九章算术》中有这样一个题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别放在一起而且用称称重,5只雀总重量比6只燕的总重量要重、若交换一只雀、一只燕,它们重量相等,5只雀,6只燕重量为1斤.问每1只雀、燕各重多少斤?”设每一只雀的重量为x斤,每一只燕的重量为y斤,则可建立方程组为( )
A. B.
C. D.
11若整数a使关于x的分式方程+=1的解为正整数,且使关于y的不等式组有解,则满足条件的整数a的值之积是( )
A.﹣4 B.0 C.16 D.64
二次函数 图象如图,下列结论:
① ;②若
③ ;当 时, 其中正确的有( )
B
C. D.
二、填空题:(本大题4个小题,每小题4分,共16分)请将每小题的答案直接填在答题卡中对应的横线上
13. 3﹣1+(3﹣π)0=___________.
14. 在学校开设的数学学科校本课程学习中,张敏和黎明分别在《数学与生活》《数学与天文》《数学与实验》中随机选择一门,两人恰好选中同一门课程的概率为__________.
15. 在平行四边形ABCD中,P为AB上一点,BP=3,BC=3,∠A=60°,以B为圆心,BP为半径画弧与CD交于点E,并刚好经过C点,则阴影部分面积为__________(结果保留π).
金鹏手机专卖店以相同的价格购进A、B两种手机,并将A、B两种手机分别按利润率50%和80%定价销售.一段时间后,分别售出各自总进货量的30%和50%,此时,A、B两种手机的营业额之比为3:5.为迎接店庆十周年,商店决定将B种手机降价销售,A种手机价格不变,最终全部售完,已知A、B两种手机的总利润之比为20:21,则B种手机在降价销售时的利润率为_________.
三、解答题:(本大题8个小题,共76分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡中对应的位置上
17.化简:
(1)(x+y)(x﹣y)+(x﹣2y)2; (2)(1﹣)÷.
18.如图,山顶上有一个信号塔AC,已知信号塔高AC=15米,在山脚下点B处测得塔底C的仰角∠CBD=36.9°,塔顶A的仰角∠ABD=42.0°,求山高CD(点A,C,D在同一条竖直线上).
(参考数据:tan36.9°≈0.75,sin36.9°≈0.60,tan42.0°≈0.90.)
19. 在四边形ABCD中,∠B=90°,AD∥BC,AD=CD.
(1)用尺规作∠ADC的平分线(基本作图,保留作图痕迹,不写作法);
(2)在(1)的情形下,设∠ADC的平分线交BC于点F,连接AF,猜想四边形AFCD是哪种特殊的平行四边形?并证明你的猜想.
20.钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据:
甲小区:
乙小区:
整理数据:
成绩(分)
甲小区
乙小区
分析数据:
统计量 平均数 中位数 众数
甲小区
乙小区
应用数据:
(1)填空:________,________,________,________;
(2)若甲小区共有人参与答卷,请估计甲小区成绩大于分的人数;
(3)根据以上数据,________(填“甲”或“乙”)小区对新型冠状病毒肺炎防护知识掌握得更好,理由____________________________________________________________________
21.如图,已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2),一次函数的图象交x轴于点C.
(1)求这两个函数的关系式;
(2)求△AOB的面积;
(3)结合图象直接写出y1>y2时,x的取值范围.
22.为响应国家号召,帮助农副产品走出大山,“村头”电商平台将咸蛋和豆腐乳进行网上销售.咸蛋售价为4元/袋,豆腐乳售价为5元/袋,5月份咸蛋的销量比豆腐乳的销量多1200袋,五月份咸蛋的总销售额为豆腐乳总销售额的两倍.
(1)5月份咸蛋和豆腐乳的销售量分别为多少袋?
(2)6月份咸蛋售价比5月份降低了a%,销量比5月份增加了a%.豆腐乳的销量比5月份增加了a%,售价保持不变,结果咸蛋和豆腐乳6月份的总销售额比5月份增加a%,求a的值.
23.阅读下列材料,解决问题.
【材料1】对于任意一个多位数,如果它的各位数字之和除以一个正整数n所得的余数与它自身除以这个正整数n所得的余数相同,我们就称这个多位数是n的“余同数”.例如:对于多位数2714,2714÷3=904…2,且(2+7+1+4)÷3=4…2,则2714是3的“余同数”.
【材料2】对于任意两个多位数A,B,若A除以正整数n所得的余数与B除以正整数n所得的余数相同,则A与B的差一定能被n整除.
(1)判断3142是否是5的“余同数”,并说明理由;
(2)若一个三位数是7的“余同数”,它的百位数字与十位数字之和小于9,个位数字比百位数字大1,求所有符合条件的三位数.
24.如图1所示,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A和B两点,与y轴交于点C;直线y=x+3经过点A,C.
(1)求抛物线的函数表达式;
(2)点P是抛物线上位于第二象限的一个动点,求四边形ABCP面积的最大值及此时点P的坐标;
(3)如图2,将原抛物线向射线AC方向平移2个单位长度得到抛物线y1,点N为y轴上一动点,抛物线y1上是否存在点M,使以点A,B,N,M为顶点的四边形为平行四边形,若存在,请直接写出点N的坐标;若不存在,请说明理由.
四、解答题:(本大题1个小题,共10分)解答时必须给出必要的演算过程或推理步骤
25.在△ABC中,∠ABC=90°,AB=BC,以点A为旋转中心,将边AC逆时针旋转一定角度,得到线段AD,使BD∥AC,AD交BC于点G,过点C作CE⊥AD交AD于点F.
(1)若AB=3,求BD的长;
(2)求证:AG=CF+DF;
(3)点M是AC边上一动点,在线段BM上存在一点N,使NB+NA+NC的值最小时,NB的长为m,请直接用含m的式子表示NB+NA+NC的最小值.
同课章节目录
