河南省焦作市沁阳市2021-2022学年九年级下学期第二次阶段性检测数学试题(PDF版含答案)
文档属性
| 名称 | 河南省焦作市沁阳市2021-2022学年九年级下学期第二次阶段性检测数学试题(PDF版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 195.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 16:31:30 | ||
图片预览

文档简介
九年级阶段性质量检测试卷
数 学
注意事项:
1. 本试卷分试题卷和答题卡两部分,三个大题,试题卷 1-4 页,答题卡 5-8 页,满分 120
分,考试时间 100 分钟。
2. 考生应首先阅读试题卷及答题卡上的相关信息,然后在答题卡上作答,在试题卷上作答
无效。
一、选择题(每小题 3分,共 30 分)
下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填写在答题卡
指定位置。
1援 在下列函数中,y 是 x 的反比例函数的是
A. y越2x+1 B. y= 2x C. y= -姨5 yx D. x =2
2. 如图是一个几何体,则下列不是它的三视图的是
正面 A B C D
3. 王明同学遇到了这样一道题,姨3 tan(琢+10毅)=1,则锐角 琢 的度数为
A. 40毅 B. 30毅 C. 20毅 D. 10毅
4. 关于 x 的一元二次方程 x2+x-2=m,下列说法正确的是
A. 当 m=0 时,此方程有两个相等的实数根;
B. 当 m>0 时,此方程有两个不相等的实数根;
C. 当 m<0 时,此方程没有实数根;
D. 粤此方程的根的情况与 m 的值无关。
5. 如图,在等腰 Rt驻ABC 中,AB=AC=6,蚁A=90毅,矩形 EFGH 耘 云
的顶点 E,F分别在 AB,AC 上,点 G,H 在 BC 上.设 AE=x,矩形
EFGH 的面积为 y,则 y 与 x 的函数图象的最高点坐标为 月 H G 悦
A. (3,9) B. (3,3姨2 ) C. (3,6) D. (3,6姨2 )
6. 如图,在 驻AOB 中,顶点 O 与原点重合,蚁ABO=90毅,AB=OB,A(-2,4),点 C 为边 OA 上
一点,且 OA=4OC.将 驻AOB 向右平移,当点 C 的对应点 C忆恰好 y
落在直线 y=-x+4 A上时,点 B 的对应点 B忆的坐标为
A. (2,1) B. ( 12 ,1 ) y越-x+4B C荫
C. (4,2) D.(12 ,2) O x
九年级数学 第 1 页(共 8 页)
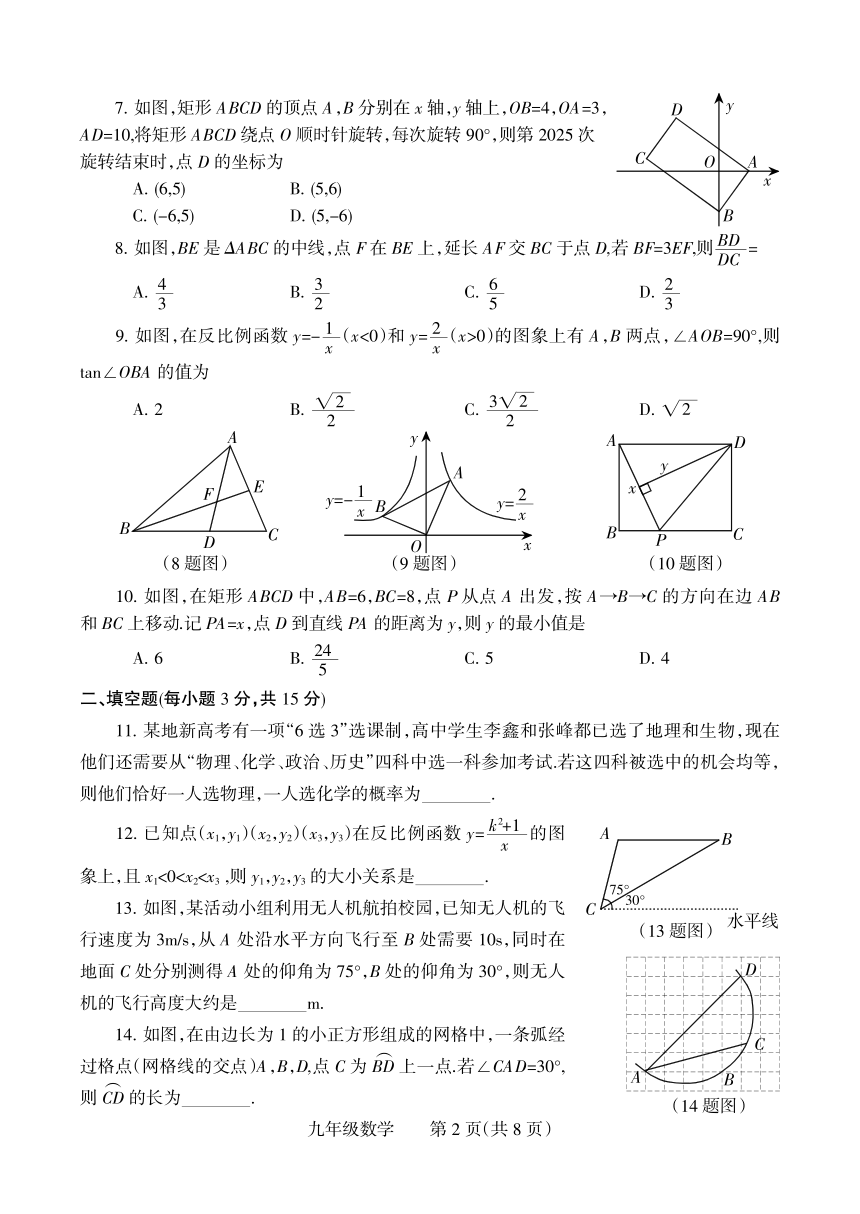
7. 如图,矩形 ABCD 的顶点 A,B 分别在 x 轴,y 轴上,OB=4,OA=3, D 赠
AD=10,将矩形 ABCD 绕点 O 顺时针旋转,每次旋转 90毅,则第 2025 次
旋转结束时,点 D 的坐标为 C 韵 粤
A. (6,5) B. (5,6) 曾
C. (-6,5) D. (5,-6) 月
8. 如图,BE 是 驻ABC 的中线,点 F在 BE 上,延长 AF交 BC 于点 D,若 BF=3EF,则 BDDC =
A. 34 B. 32 C. 56 D. 23
9. 如图,在反比例函数 y=- 1x(x<0)和 y= 2x(x>0)的图象上有 A,B 两点,蚁AOB=90毅,则
tan蚁OBA 的值为
A. 2 B. 姨22 C. 3姨2 2 D. 姨2
A 赠 A D
赠
F E y=- 1
粤
曾
x 月 y=
2
x
B
D C B
8 韵 曾
P C
( 题图) (9 题图) (10 题图)
10. 如图,在矩形 ABCD 中,AB=6,BC=8,点 P从点 A 出发,按 A寅B寅C 的方向在边 AB
和 BC 上移动.记 PA=x,点 D 到直线 PA 的距离为 y,则 y 的最小值是
A. 6 B. 254 C. 5 D. 4
二、填空题(每小题 3分,共 15分)
11. 某地新高考有一项“6 选 3”选课制,高中学生李鑫和张峰都已选了地理和生物,现在
他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,
则他们恰好一人选物理,一人选化学的概率为 .
12. 已知点(x1,y1)(x2,y2)(x3,y3)在反比例函数 y= k2+1x 的图 A B
象上,且 x1<013. 75毅如图,某活动小组利用无人机航拍校园,已知无人机的飞 C 30毅
水平线
行速度为 3m/s,从 A 处沿水平方向飞行至 B 处需要 10s,同时在 (13 题图)
地面 C 处分别测得 A 处的仰角为 75毅,B 处的仰角为 30毅,则无人 D
机的飞行高度大约是 m.
14. 如图,在由边长为 1 的小正方形组成的网格中,一条弧经 C
过格点(网格线的交点)A,B,D,点 C 为 BD 上一点.若蚁CAD=30毅, A B
则 CD 的长为 . (14 题图)
九年级数学 第 2 页(共 8 页)
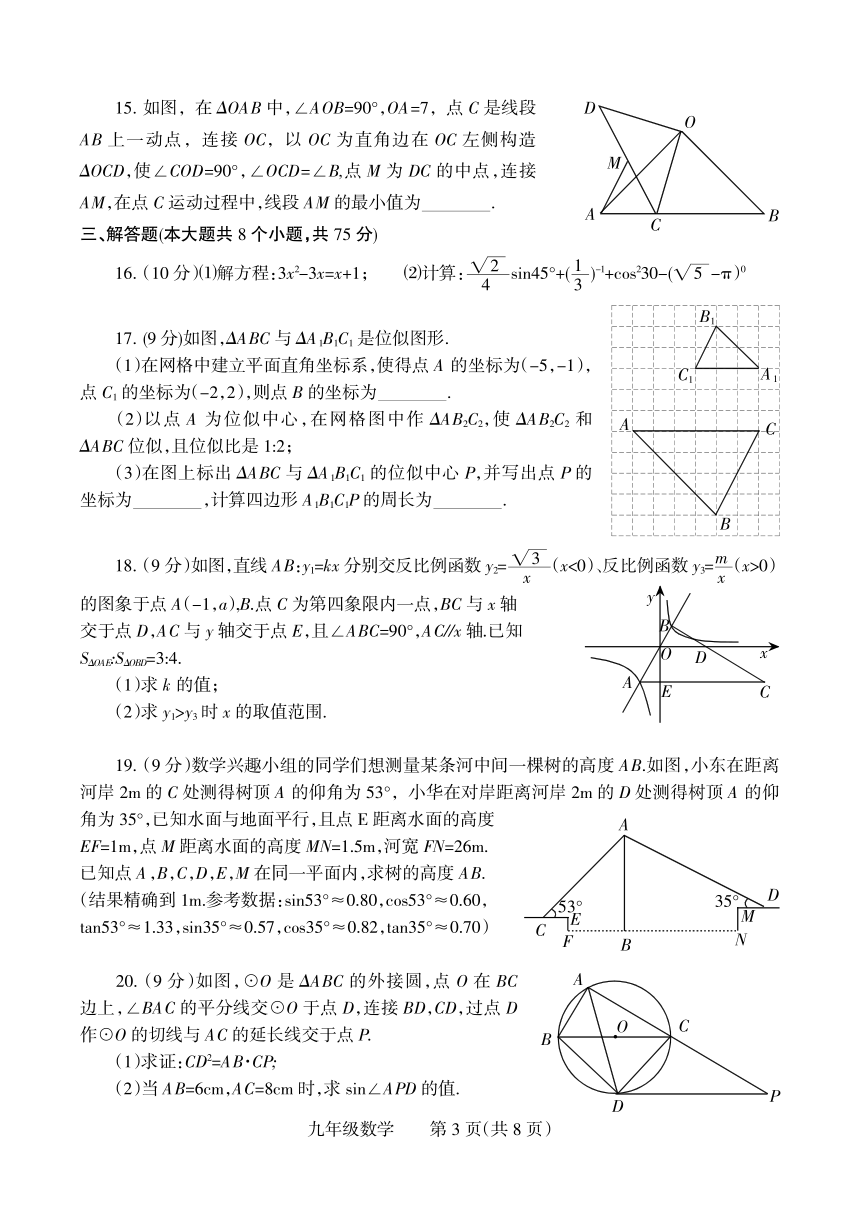
15. 如图,在 驻OAB 中,蚁AOB=90毅,OA=7,点 C 是线段 D
O
AB 上一动点,连接 OC,以 OC 为直角边在 OC 左侧构造
驻OCD,使蚁COD=90毅,蚁OCD=蚁B,点 M 为 DC 的中点,连接 M
AM,在点 C 运动过程中,线段 AM 的最小值为 . A B
三、解答题(本大题共 8 个小题,共 75 分) C
16.(10 分)优解方程:3x2-3x=x+1; 悠计算:姨42 sin45毅+( 13 )-1+cos230-(姨5 -仔)0
B
17. (9 1分)如图,驻ABC 与 驻A 1B1C1 是位似图形.
(1)在网格中建立平面直角坐标系,使得点 A 的坐标为(-5,-1),
点 C1 的坐标为(-2,2),则点 B 的坐标为 . C1 A 1
(2)以点 A 为位似中心,在网格图中作 驻AB2C2,使 驻AB2C2 和 A C
驻ABC 位似,且位似比是 1:2;
(3)在图上标出 驻ABC 与 驻A 1B1C1 的位似中心 P,并写出点 P的
坐标为 ,计算四边形 A 1B1C1P的周长为 .
B
18.(9 分)如图,直线 AB:y1=kx分别交反比例函数 y2= 姨3x (x<0)、反比例函数 y3=mx(x>0)
的图象于点 A(-1,a),B.点 C 为第四象限内一点,BC 与 x 轴 y
交于点 D,AC 与 y 轴交于点 E,且蚁ABC=90毅,AC//x 轴.已知 B
S驻OAE:S驻OBD=3:4. O D x
(1)求 k 的值; A
(2)求 y1>y3 时 x 的取值范围.
E C
19.(9 分)数学兴趣小组的同学们想测量某条河中间一棵树的高度 AB.如图,小东在距离
河岸 2m 的 C 处测得树顶 A 的仰角为 53毅,小华在对岸距离河岸 2m 的 D 处测得树顶 A 的仰
角为 35毅,已知水面与地面平行,且点 E 距离水面的高度 A
EF=1m,点 M 距离水面的高度 MN=1.5m,河宽 FN=26m.
已知点 A,B,C,D,E,M 在同一平面内,求树的高度 AB.
(结果精确到 1m.参考数据:sin53毅抑0.80,cos53毅抑0.60, 35毅 D
tan53毅抑1.33,sin35毅抑0.57,cos35毅抑0.82,tan35毅抑0.70 53毅 M) C EF B N
20.(9 分)如图,已O 是 驻ABC 的外接圆,点 O 在 BC A
边上,蚁BAC 的平分线交已O 于点 D,连接 BD,CD,过点 D
作已O 的切线与 AC 的延长线交于点 P. O CB 荫
(1)求证:CD2=AB·CP;
(2)当 AB=6cm,AC=8cm 时,求 sin蚁APD 的值.
D P
九年级数学 第 3 页(共 8 页)
21.(9 分)某公司电商平台,在 2021 年五一长假期间,举行了 x 30 50 80
商品打折促销活动,经市场调查发现,某种商品的周销售量 y(件)是
关于售价 x(元/件)的一次函数,右表仅列出了该商品的售价 x,周销 y 140 100 40
售量 y,周销售利润 W(元)的三组对应值数据援
1 W 1400 3000 2400( )求 y 关于 x 的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价 a(元/件),售价 x为多少时,周销售利润W 最大?并求出此时的最大利润;
(3)因疫情期间,该商品进价提高了 m(元/件)(m跃0),公司为回馈消费者,规定该商品售价
x 不得超过 55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,
若周销售最大利润是 2700 元,求 m 的值援
22.(10 分)如图,抛物线 y=ax2+bx+c 的顶点 G 的坐标为(-1,-4),与 x 轴交于 A,B 两点,
且 AB=4. y
(1)求此抛物线的解析式.
(2)已知点(x1,y1)(x1+1,y2)均在此抛物线上,且 y2x1 的取值范围. A O B x
(3)将该抛物线沿 x 轴平移,当抛物线与坐标轴有且只有两个交
点时停止移动,得到新抛物线 L,点 M 是线段 AB(A,B 为原抛物线
与 x 轴的交点)上的一点,过点 M 作 MN彝x 轴交新抛物线 L 于点 N, G
求点 N 的纵坐标 yN 的取值范围.
23.(10 分)在 驻ABC 中,AB=AC,蚁BAC=琢,点 P是平面内不与点 B,C 重合的一动点,连接
PC,将线段 PC 绕点 P顺时针旋转 琢 得到线段 PQ,连接 BQ,CQ,AP,点 M,N 分别是线段 CB,
CQ 的中点,连接 MN.
(1)【观察猜想】如图(1)当点 P与点 B 在直线 CA 两侧,琢=60毅时,MNPA 的值是 ,
直线 MN 与直线 PA 所成的锐角的度数是 ;
(2)【类比探究】如图(2)当点 P与点 B 在直线 CA 两侧,琢=120毅时,求MNPA 的值及直线 MN
与直线 PA 所成的锐角的度数;
(3)【解决问题】当点 P在直线 BC 上方,琢=90毅,且点 A,P,Q 在同一条直线上时,连接 BP,
已知 S 1 MN驻BCP= 2 S驻BCA,请直接写出 CP 的值.
A Q A
P P
A
Q NN
B M C B M C B C
图 1 图 2 备用图
九年级数学 第 4 页(共 8 页)
九年级阶段性质量检测试卷
数学参考答案及评分标准
一、选择题(每小题 3 分,共 30分)
1. C 2. C 3. C 4. 月 5. A 6. B 7. A 8. B 9. D 10. B
二、填空题(每小题 3 分,共 15分)
11援 18 12援 y2跃y3跃y1 13援 15+125姨3 14援 姨3员猿 仔 15援 72
三、解答题(本大题共 8个小题,满分 75分)
16(. 1)x1= 2+姨3 7 x2= 2-姨3 7 (2)3
17(. 1)(-1,-5) (2)略; (3)(-1,1) 2姨5 +3姨2
18(. 1)疫 点 A(-1,a)在反比例函数 y2= 姨3x 的图象上, 亦 a=-姨3
把 A(-1,-姨3 )代入 y1=kx,可得-姨3 =-k, 亦 k=姨3
(2)疫AC//x 轴, 亦 蚁OAC=蚁BOD,蚁AEO=90毅=蚁ABC,
2
亦驻AEO易驻OBD 亦 AE S驻AEO 3OB2 = S =驻OBD 4
又 疫AE=1, 亦OB= 2姨3 3
由直线 AB 的解析式为 y=姨3 x,可设 B(b,姨3 b)(b>0)
亦b2+(姨3 b)2越(2姨3 3 )2 亦b越 姨33 亦B(姨33 ,1)
结合图象可知,y1>y3 时,x 的取值范围为 x> 姨33 .
19.解:过点 C 作 CH彝AB 于点 H,过点 D 作 DG彝AB 于点 G,
设 CH 为 xm,tan蚁ACH= AHCH ,AH=1.33xm,DG=(26+2+2-x)=(30-x)m
AG=AH-GH=1.33x-(1.5-1)=(1.33x-0.5)m
tan蚁ADG= AGDG tan35毅= 1.3330x--0.5x 亦x抑10.59
亦AB越AH+1越1.33伊10.59+1抑15(m)
20(. 1)证明:连接 OD,疫BC 是已O 的直径 亦蚁BAC=蚁BDC=90毅
又 疫AD 平分蚁BAC 亦蚁BAD=蚁CAD=45毅 亦BD=CD
亦BD=CD 蚁DBC=蚁DCB=45毅 又 疫CO=OD 亦 蚁ODC=45毅
疫DP是已O 的切线,切点为 D 亦蚁ODP=90毅 亦蚁CDP=45毅
亦蚁CAD=蚁CDP四边形 ABDC 为圆内接四边形
亦蚁ABD=蚁CDP 亦驻ABD易驻DCP 亦 ABCD = BDCP 又 疫BD=CD 亦CD2越AB·CP
(2)过点 C 作 CE彝DP于点 E
BC越姨AB2+AC2 越10cm CD越 BC姨2 越5姨2 又 疫BD=CD 亦CD越5姨2 cm
又 疫CD2=AB·CP 亦CP越 235 cm
又 疫蚁CDP=45毅 CE越5cm 亦sin蚁APD= CE 3
2-CP
越 5
九年级数学答案 1
21(. 1)y=-2x+200 (任选两组 x,y 的值代入 y=kx+b,求出 k 和 b)
(2)疫140(30-a)=1400 亦a=20
w=(x-20)(-2x+200)=-2x2+240x-4000=-2(x-60)2+3200
亦 售价为 60 元时,周销售利润最大为 3200 元。
(3)w=(x-20-m)(-2x+200)=-2(x-60- 12 m)-200m-4000
疫x臆55 在对称轴左侧,w 随 x 的增大而增大
当 x=55 时,w 最大=2700 (55-20-m)(-2伊55+200)=2700
亦m=5
22(. 1)y=x2+2x-3 (2)x1<- 32
(3)淤当 B 与 O 重合时,-4臆yN臆5于当 A 与 O 重合时,-3臆yN臆21
23(. 1)12 ;60毅
(2)如图(2)设 MN 交 CA 于点 H 延长 MN 交 PA 于点 I. AC=AB,PC=PQ,蚁CPQ=蚁CAB=120毅.
蚁PCO=蚁ACB=30毅 亦驻PCQ 易驻ACB. CPCA 越 CQCB
又 疫CM=MB CN=NQ, 亦 CQ 越 CN 亦 CP 越 CN 亦 CP 越 CACB CM CA CM CN CM
又 疫蚁NCM=蚁NCH+蚁ACB=蚁NCH+蚁PCQ=蚁PCA,亦驻CAP易驻CMN,
亦蚁CAP=蚁CMN, MNPA 越 CMCA
连接 AM,疫CM=MB,AB=AC, 亦AM彝BC,
CM
CA 越cos蚁ACB= 姨2猿 亦MN 姨猿PA = 2
疫蚁AHI=蚁CHM,蚁IAH=蚁CMH,
亦蚁AIM=蚁ACM=30毅
亦 直线 MN 与直线 PA 所成的锐角为 30毅
(3)MN 的值为 2-姨CP 2 2 或 2+姨2 2
九年级数学答案 2-2
数 学
注意事项:
1. 本试卷分试题卷和答题卡两部分,三个大题,试题卷 1-4 页,答题卡 5-8 页,满分 120
分,考试时间 100 分钟。
2. 考生应首先阅读试题卷及答题卡上的相关信息,然后在答题卡上作答,在试题卷上作答
无效。
一、选择题(每小题 3分,共 30 分)
下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填写在答题卡
指定位置。
1援 在下列函数中,y 是 x 的反比例函数的是
A. y越2x+1 B. y= 2x C. y= -姨5 yx D. x =2
2. 如图是一个几何体,则下列不是它的三视图的是
正面 A B C D
3. 王明同学遇到了这样一道题,姨3 tan(琢+10毅)=1,则锐角 琢 的度数为
A. 40毅 B. 30毅 C. 20毅 D. 10毅
4. 关于 x 的一元二次方程 x2+x-2=m,下列说法正确的是
A. 当 m=0 时,此方程有两个相等的实数根;
B. 当 m>0 时,此方程有两个不相等的实数根;
C. 当 m<0 时,此方程没有实数根;
D. 粤此方程的根的情况与 m 的值无关。
5. 如图,在等腰 Rt驻ABC 中,AB=AC=6,蚁A=90毅,矩形 EFGH 耘 云
的顶点 E,F分别在 AB,AC 上,点 G,H 在 BC 上.设 AE=x,矩形
EFGH 的面积为 y,则 y 与 x 的函数图象的最高点坐标为 月 H G 悦
A. (3,9) B. (3,3姨2 ) C. (3,6) D. (3,6姨2 )
6. 如图,在 驻AOB 中,顶点 O 与原点重合,蚁ABO=90毅,AB=OB,A(-2,4),点 C 为边 OA 上
一点,且 OA=4OC.将 驻AOB 向右平移,当点 C 的对应点 C忆恰好 y
落在直线 y=-x+4 A上时,点 B 的对应点 B忆的坐标为
A. (2,1) B. ( 12 ,1 ) y越-x+4B C荫
C. (4,2) D.(12 ,2) O x
九年级数学 第 1 页(共 8 页)
7. 如图,矩形 ABCD 的顶点 A,B 分别在 x 轴,y 轴上,OB=4,OA=3, D 赠
AD=10,将矩形 ABCD 绕点 O 顺时针旋转,每次旋转 90毅,则第 2025 次
旋转结束时,点 D 的坐标为 C 韵 粤
A. (6,5) B. (5,6) 曾
C. (-6,5) D. (5,-6) 月
8. 如图,BE 是 驻ABC 的中线,点 F在 BE 上,延长 AF交 BC 于点 D,若 BF=3EF,则 BDDC =
A. 34 B. 32 C. 56 D. 23
9. 如图,在反比例函数 y=- 1x(x<0)和 y= 2x(x>0)的图象上有 A,B 两点,蚁AOB=90毅,则
tan蚁OBA 的值为
A. 2 B. 姨22 C. 3姨2 2 D. 姨2
A 赠 A D
赠
F E y=- 1
粤
曾
x 月 y=
2
x
B
D C B
8 韵 曾
P C
( 题图) (9 题图) (10 题图)
10. 如图,在矩形 ABCD 中,AB=6,BC=8,点 P从点 A 出发,按 A寅B寅C 的方向在边 AB
和 BC 上移动.记 PA=x,点 D 到直线 PA 的距离为 y,则 y 的最小值是
A. 6 B. 254 C. 5 D. 4
二、填空题(每小题 3分,共 15分)
11. 某地新高考有一项“6 选 3”选课制,高中学生李鑫和张峰都已选了地理和生物,现在
他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,
则他们恰好一人选物理,一人选化学的概率为 .
12. 已知点(x1,y1)(x2,y2)(x3,y3)在反比例函数 y= k2+1x 的图 A B
象上,且 x1<0
水平线
行速度为 3m/s,从 A 处沿水平方向飞行至 B 处需要 10s,同时在 (13 题图)
地面 C 处分别测得 A 处的仰角为 75毅,B 处的仰角为 30毅,则无人 D
机的飞行高度大约是 m.
14. 如图,在由边长为 1 的小正方形组成的网格中,一条弧经 C
过格点(网格线的交点)A,B,D,点 C 为 BD 上一点.若蚁CAD=30毅, A B
则 CD 的长为 . (14 题图)
九年级数学 第 2 页(共 8 页)
15. 如图,在 驻OAB 中,蚁AOB=90毅,OA=7,点 C 是线段 D
O
AB 上一动点,连接 OC,以 OC 为直角边在 OC 左侧构造
驻OCD,使蚁COD=90毅,蚁OCD=蚁B,点 M 为 DC 的中点,连接 M
AM,在点 C 运动过程中,线段 AM 的最小值为 . A B
三、解答题(本大题共 8 个小题,共 75 分) C
16.(10 分)优解方程:3x2-3x=x+1; 悠计算:姨42 sin45毅+( 13 )-1+cos230-(姨5 -仔)0
B
17. (9 1分)如图,驻ABC 与 驻A 1B1C1 是位似图形.
(1)在网格中建立平面直角坐标系,使得点 A 的坐标为(-5,-1),
点 C1 的坐标为(-2,2),则点 B 的坐标为 . C1 A 1
(2)以点 A 为位似中心,在网格图中作 驻AB2C2,使 驻AB2C2 和 A C
驻ABC 位似,且位似比是 1:2;
(3)在图上标出 驻ABC 与 驻A 1B1C1 的位似中心 P,并写出点 P的
坐标为 ,计算四边形 A 1B1C1P的周长为 .
B
18.(9 分)如图,直线 AB:y1=kx分别交反比例函数 y2= 姨3x (x<0)、反比例函数 y3=mx(x>0)
的图象于点 A(-1,a),B.点 C 为第四象限内一点,BC 与 x 轴 y
交于点 D,AC 与 y 轴交于点 E,且蚁ABC=90毅,AC//x 轴.已知 B
S驻OAE:S驻OBD=3:4. O D x
(1)求 k 的值; A
(2)求 y1>y3 时 x 的取值范围.
E C
19.(9 分)数学兴趣小组的同学们想测量某条河中间一棵树的高度 AB.如图,小东在距离
河岸 2m 的 C 处测得树顶 A 的仰角为 53毅,小华在对岸距离河岸 2m 的 D 处测得树顶 A 的仰
角为 35毅,已知水面与地面平行,且点 E 距离水面的高度 A
EF=1m,点 M 距离水面的高度 MN=1.5m,河宽 FN=26m.
已知点 A,B,C,D,E,M 在同一平面内,求树的高度 AB.
(结果精确到 1m.参考数据:sin53毅抑0.80,cos53毅抑0.60, 35毅 D
tan53毅抑1.33,sin35毅抑0.57,cos35毅抑0.82,tan35毅抑0.70 53毅 M) C EF B N
20.(9 分)如图,已O 是 驻ABC 的外接圆,点 O 在 BC A
边上,蚁BAC 的平分线交已O 于点 D,连接 BD,CD,过点 D
作已O 的切线与 AC 的延长线交于点 P. O CB 荫
(1)求证:CD2=AB·CP;
(2)当 AB=6cm,AC=8cm 时,求 sin蚁APD 的值.
D P
九年级数学 第 3 页(共 8 页)
21.(9 分)某公司电商平台,在 2021 年五一长假期间,举行了 x 30 50 80
商品打折促销活动,经市场调查发现,某种商品的周销售量 y(件)是
关于售价 x(元/件)的一次函数,右表仅列出了该商品的售价 x,周销 y 140 100 40
售量 y,周销售利润 W(元)的三组对应值数据援
1 W 1400 3000 2400( )求 y 关于 x 的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价 a(元/件),售价 x为多少时,周销售利润W 最大?并求出此时的最大利润;
(3)因疫情期间,该商品进价提高了 m(元/件)(m跃0),公司为回馈消费者,规定该商品售价
x 不得超过 55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,
若周销售最大利润是 2700 元,求 m 的值援
22.(10 分)如图,抛物线 y=ax2+bx+c 的顶点 G 的坐标为(-1,-4),与 x 轴交于 A,B 两点,
且 AB=4. y
(1)求此抛物线的解析式.
(2)已知点(x1,y1)(x1+1,y2)均在此抛物线上,且 y2
(3)将该抛物线沿 x 轴平移,当抛物线与坐标轴有且只有两个交
点时停止移动,得到新抛物线 L,点 M 是线段 AB(A,B 为原抛物线
与 x 轴的交点)上的一点,过点 M 作 MN彝x 轴交新抛物线 L 于点 N, G
求点 N 的纵坐标 yN 的取值范围.
23.(10 分)在 驻ABC 中,AB=AC,蚁BAC=琢,点 P是平面内不与点 B,C 重合的一动点,连接
PC,将线段 PC 绕点 P顺时针旋转 琢 得到线段 PQ,连接 BQ,CQ,AP,点 M,N 分别是线段 CB,
CQ 的中点,连接 MN.
(1)【观察猜想】如图(1)当点 P与点 B 在直线 CA 两侧,琢=60毅时,MNPA 的值是 ,
直线 MN 与直线 PA 所成的锐角的度数是 ;
(2)【类比探究】如图(2)当点 P与点 B 在直线 CA 两侧,琢=120毅时,求MNPA 的值及直线 MN
与直线 PA 所成的锐角的度数;
(3)【解决问题】当点 P在直线 BC 上方,琢=90毅,且点 A,P,Q 在同一条直线上时,连接 BP,
已知 S 1 MN驻BCP= 2 S驻BCA,请直接写出 CP 的值.
A Q A
P P
A
Q NN
B M C B M C B C
图 1 图 2 备用图
九年级数学 第 4 页(共 8 页)
九年级阶段性质量检测试卷
数学参考答案及评分标准
一、选择题(每小题 3 分,共 30分)
1. C 2. C 3. C 4. 月 5. A 6. B 7. A 8. B 9. D 10. B
二、填空题(每小题 3 分,共 15分)
11援 18 12援 y2跃y3跃y1 13援 15+125姨3 14援 姨3员猿 仔 15援 72
三、解答题(本大题共 8个小题,满分 75分)
16(. 1)x1= 2+姨3 7 x2= 2-姨3 7 (2)3
17(. 1)(-1,-5) (2)略; (3)(-1,1) 2姨5 +3姨2
18(. 1)疫 点 A(-1,a)在反比例函数 y2= 姨3x 的图象上, 亦 a=-姨3
把 A(-1,-姨3 )代入 y1=kx,可得-姨3 =-k, 亦 k=姨3
(2)疫AC//x 轴, 亦 蚁OAC=蚁BOD,蚁AEO=90毅=蚁ABC,
2
亦驻AEO易驻OBD 亦 AE S驻AEO 3OB2 = S =驻OBD 4
又 疫AE=1, 亦OB= 2姨3 3
由直线 AB 的解析式为 y=姨3 x,可设 B(b,姨3 b)(b>0)
亦b2+(姨3 b)2越(2姨3 3 )2 亦b越 姨33 亦B(姨33 ,1)
结合图象可知,y1>y3 时,x 的取值范围为 x> 姨33 .
19.解:过点 C 作 CH彝AB 于点 H,过点 D 作 DG彝AB 于点 G,
设 CH 为 xm,tan蚁ACH= AHCH ,AH=1.33xm,DG=(26+2+2-x)=(30-x)m
AG=AH-GH=1.33x-(1.5-1)=(1.33x-0.5)m
tan蚁ADG= AGDG tan35毅= 1.3330x--0.5x 亦x抑10.59
亦AB越AH+1越1.33伊10.59+1抑15(m)
20(. 1)证明:连接 OD,疫BC 是已O 的直径 亦蚁BAC=蚁BDC=90毅
又 疫AD 平分蚁BAC 亦蚁BAD=蚁CAD=45毅 亦BD=CD
亦BD=CD 蚁DBC=蚁DCB=45毅 又 疫CO=OD 亦 蚁ODC=45毅
疫DP是已O 的切线,切点为 D 亦蚁ODP=90毅 亦蚁CDP=45毅
亦蚁CAD=蚁CDP四边形 ABDC 为圆内接四边形
亦蚁ABD=蚁CDP 亦驻ABD易驻DCP 亦 ABCD = BDCP 又 疫BD=CD 亦CD2越AB·CP
(2)过点 C 作 CE彝DP于点 E
BC越姨AB2+AC2 越10cm CD越 BC姨2 越5姨2 又 疫BD=CD 亦CD越5姨2 cm
又 疫CD2=AB·CP 亦CP越 235 cm
又 疫蚁CDP=45毅 CE越5cm 亦sin蚁APD= CE 3
2-CP
越 5
九年级数学答案 1
21(. 1)y=-2x+200 (任选两组 x,y 的值代入 y=kx+b,求出 k 和 b)
(2)疫140(30-a)=1400 亦a=20
w=(x-20)(-2x+200)=-2x2+240x-4000=-2(x-60)2+3200
亦 售价为 60 元时,周销售利润最大为 3200 元。
(3)w=(x-20-m)(-2x+200)=-2(x-60- 12 m)-200m-4000
疫x臆55 在对称轴左侧,w 随 x 的增大而增大
当 x=55 时,w 最大=2700 (55-20-m)(-2伊55+200)=2700
亦m=5
22(. 1)y=x2+2x-3 (2)x1<- 32
(3)淤当 B 与 O 重合时,-4臆yN臆5于当 A 与 O 重合时,-3臆yN臆21
23(. 1)12 ;60毅
(2)如图(2)设 MN 交 CA 于点 H 延长 MN 交 PA 于点 I. AC=AB,PC=PQ,蚁CPQ=蚁CAB=120毅.
蚁PCO=蚁ACB=30毅 亦驻PCQ 易驻ACB. CPCA 越 CQCB
又 疫CM=MB CN=NQ, 亦 CQ 越 CN 亦 CP 越 CN 亦 CP 越 CACB CM CA CM CN CM
又 疫蚁NCM=蚁NCH+蚁ACB=蚁NCH+蚁PCQ=蚁PCA,亦驻CAP易驻CMN,
亦蚁CAP=蚁CMN, MNPA 越 CMCA
连接 AM,疫CM=MB,AB=AC, 亦AM彝BC,
CM
CA 越cos蚁ACB= 姨2猿 亦MN 姨猿PA = 2
疫蚁AHI=蚁CHM,蚁IAH=蚁CMH,
亦蚁AIM=蚁ACM=30毅
亦 直线 MN 与直线 PA 所成的锐角为 30毅
(3)MN 的值为 2-姨CP 2 2 或 2+姨2 2
九年级数学答案 2-2
同课章节目录
