2022届高三数学二轮复习-统计和概率模块 课件(29张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习-统计和概率模块 课件(29张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 16:37:59 | ||
图片预览



文档简介
(共29张PPT)
二轮复习--统计和概率模块
一、强化知识点,形成知识网络,
重视边缘知识;
二、规范答题步骤,加强书写表达
训练,向步骤要分;
三、找到增分点,注重通性通法,
提高运算能力。
高考真题考点统计
思
维
导
图
思
维
导
图
思
维
导
图
思
维
导
图
思
维
导
图
思
维
导
图
思
维
导
图
题型归纳
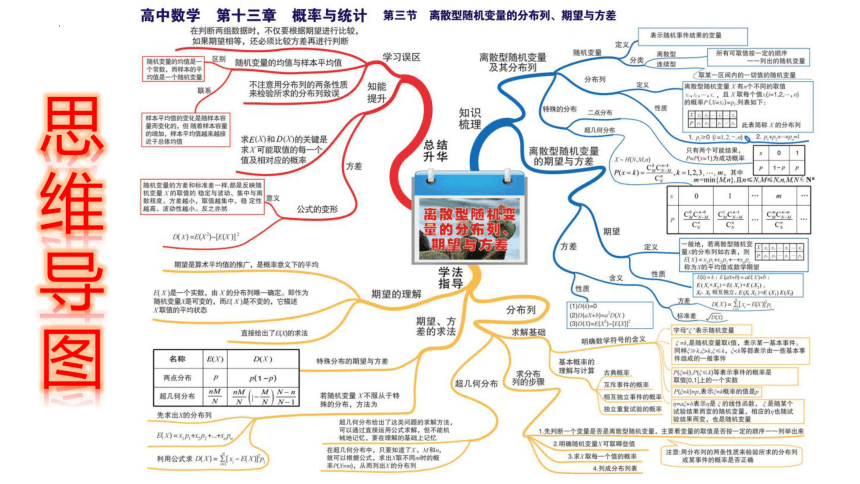
一、 离散型随机变量的分布列
题型归纳
二、 线性回归方程
题型归纳
二、 线性回归方程
题型归纳
三、 独立性检验
题型归纳
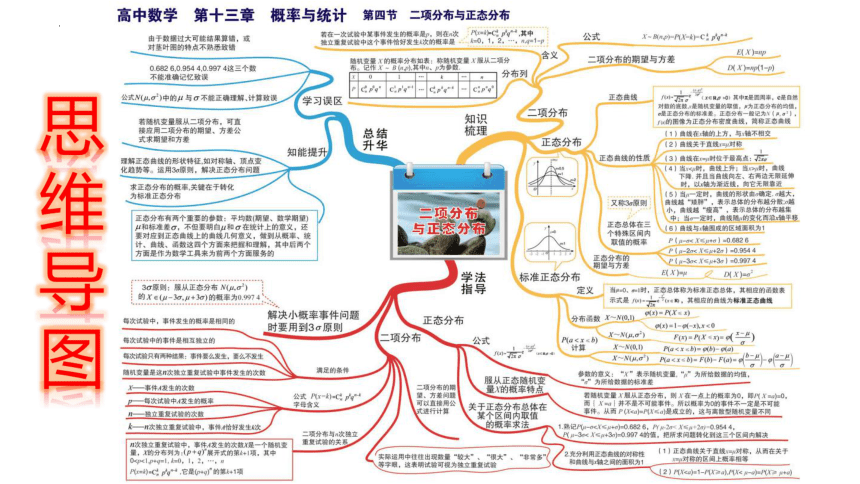
四、 二项分布与正态分布
真题研透·明技法
考场练兵·提素养
课堂小结
2.思维导图
1.考点归纳
3.题型归纳
4.高考真题演练
高中数学
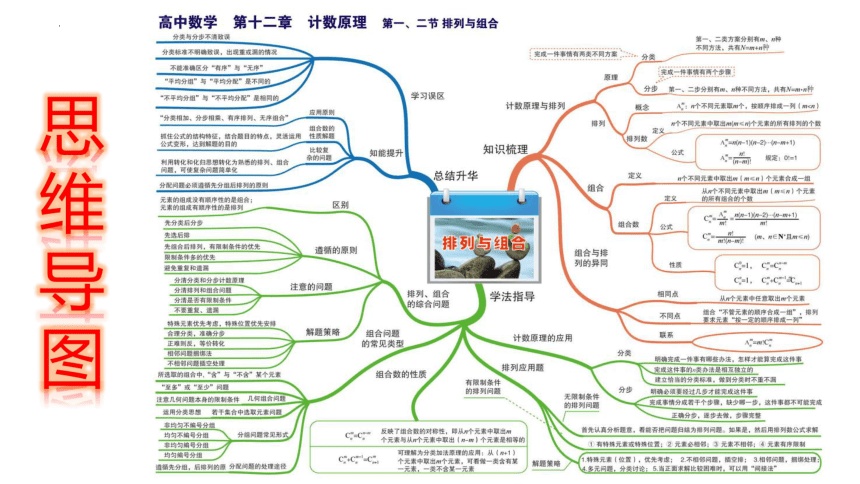
第十二章
计数原理第一、二节排列与组合
分类与分步不清致误
第一、二类方案分别有m、n种
分类标准不明确致误,出现重或漏的情况
不同方法,共有N=m+n种
完成一件事情有两类不同方案
分类
不能准确区分“有序”与“无序”
完成一件事情有两个步骤
“平均分组”与“平均分配”是不同的
原理
分步
第一、二步分别有m、种不同方法,共有N=m:n种
“不平均分组”与“不平均分配”是相同的
学习误区
计数原理与排列
概念
A:n个不同元素取m个,按顺序排成一列(m应用原则
“分类相加、分步相乘、有序排列、无序组合”
排列
个不同元素中取出m(m≤)个元素的所有排列的个数
组合数的
定义
抓住公式的结构特征,结合题目的特点,灵活运用
性质解题
排列数
公式变形,达到解题的目的
知识梳理
A=n-10n-2…n-m+1)
比较复
杂的问题
知能提升
公式
利用转化和化归思想转化为熟悉的排列、组合
A"-(n-m)!
规定:0=1
问题,可使复杂问题简单化
总结升华
定义
n个不同元素中取出m(m≤n)个元素合成一组
分配问题必须遵循先分组后排列的原则
组合
从n个不同元素中取出m(m≤)个元素
元素的组成没有顺序性的是组合
定义
的所有组合的个数
元素的组成有顺序性的是排列
区别
C4
=nn-10m-2-n-m+1)
先分类后分步
组合数
公式
m
m!
先选后排
C=
m!(n-m!
(m、n∈N且m≤n)
先组合后排列,有限制条件的优先
遵循的原则
排列与组合
限制条件多的优先
组合与排
避免重复和遗漏
列的异同
性质
C=1,C=C
分清分类和分步计数原理
分清排列和组合问题
注意的问题
C-l,C+Cg1℃
排列、组合
分清是否有限制条件
学法指导
相同点
从n个元素中任意取出m个元素
的综合问题
不要重复、遗漏
不同点
组合“不管元素的顺序合成一组”,排列
特殊元素优先考虑,特殊位置优先安排
要求元素“按一定的顺序排成一列”
合理分类,准确分步
解题策略
组合问题
计数原理的应用
联系
正难侧反,等价转化
的常见类型
A"=m!C
相邻问题捆绑法
分类
不相邻问题插空处理
明确完成一件事有哪些办法,怎样才能算完成这件事
排列应用题
所选取的组合中,“含”与“不含”某个元素
组合数的性质
完成这件事的类办法是相互独立的
“至多”或“至少”问题
有限制条件
建立恰当的分类标准,做到分类时不重不漏
的排列问题
分步
明确必须要经过几步才能完成这件事
注意几何问题本身的限制条件几何组合问题
无限制条件
的排列问题
完成事情分成若干个步骤,缺少哪一步,这件事都不可能完成
运用分类思想若干集合中选取元素问题
正确分步,逐步去做,步骤完整
非均匀不编号分组
C=C
反映了组合数的对称性,即从个元素中取出m
首先认真分析题意,看能否把问题归结为排列问题。如果是,然后用排列数公式求解
均匀不编号分组
分组问题常见形式
个元素与从n个元素中取出(n-m】个元素是相等的
非均匀编号分组
①有特殊元素或特殊位置;2元素必相邻:③元素不相邻:④元素有序限制
均匀编号分组
可理解为分类加法原理的应用:从(+1)
CCC
个元素中取出m个元素,可看做一类含有某
解题策略
1特殊元素(位置),优先考虑;2.不相邻问题,插空排;3相邻问题,捆绑处理;
遵箭先分组,后排列的原分配问题的处理途径
一元素,一类不含某一元素
4多元问题,分类讨论:5当正面求解比较困难时,可以用“间接法”
二轮复习--统计和概率模块
一、强化知识点,形成知识网络,
重视边缘知识;
二、规范答题步骤,加强书写表达
训练,向步骤要分;
三、找到增分点,注重通性通法,
提高运算能力。
高考真题考点统计
思
维
导
图
思
维
导
图
思
维
导
图
思
维
导
图
思
维
导
图
思
维
导
图
思
维
导
图
题型归纳
一、 离散型随机变量的分布列
题型归纳
二、 线性回归方程
题型归纳
二、 线性回归方程
题型归纳
三、 独立性检验
题型归纳
四、 二项分布与正态分布
真题研透·明技法
考场练兵·提素养
课堂小结
2.思维导图
1.考点归纳
3.题型归纳
4.高考真题演练
高中数学
第十二章
计数原理第一、二节排列与组合
分类与分步不清致误
第一、二类方案分别有m、n种
分类标准不明确致误,出现重或漏的情况
不同方法,共有N=m+n种
完成一件事情有两类不同方案
分类
不能准确区分“有序”与“无序”
完成一件事情有两个步骤
“平均分组”与“平均分配”是不同的
原理
分步
第一、二步分别有m、种不同方法,共有N=m:n种
“不平均分组”与“不平均分配”是相同的
学习误区
计数原理与排列
概念
A:n个不同元素取m个,按顺序排成一列(m
“分类相加、分步相乘、有序排列、无序组合”
排列
个不同元素中取出m(m≤)个元素的所有排列的个数
组合数的
定义
抓住公式的结构特征,结合题目的特点,灵活运用
性质解题
排列数
公式变形,达到解题的目的
知识梳理
A=n-10n-2…n-m+1)
比较复
杂的问题
知能提升
公式
利用转化和化归思想转化为熟悉的排列、组合
A"-(n-m)!
规定:0=1
问题,可使复杂问题简单化
总结升华
定义
n个不同元素中取出m(m≤n)个元素合成一组
分配问题必须遵循先分组后排列的原则
组合
从n个不同元素中取出m(m≤)个元素
元素的组成没有顺序性的是组合
定义
的所有组合的个数
元素的组成有顺序性的是排列
区别
C4
=nn-10m-2-n-m+1)
先分类后分步
组合数
公式
m
m!
先选后排
C=
m!(n-m!
(m、n∈N且m≤n)
先组合后排列,有限制条件的优先
遵循的原则
排列与组合
限制条件多的优先
组合与排
避免重复和遗漏
列的异同
性质
C=1,C=C
分清分类和分步计数原理
分清排列和组合问题
注意的问题
C-l,C+Cg1℃
排列、组合
分清是否有限制条件
学法指导
相同点
从n个元素中任意取出m个元素
的综合问题
不要重复、遗漏
不同点
组合“不管元素的顺序合成一组”,排列
特殊元素优先考虑,特殊位置优先安排
要求元素“按一定的顺序排成一列”
合理分类,准确分步
解题策略
组合问题
计数原理的应用
联系
正难侧反,等价转化
的常见类型
A"=m!C
相邻问题捆绑法
分类
不相邻问题插空处理
明确完成一件事有哪些办法,怎样才能算完成这件事
排列应用题
所选取的组合中,“含”与“不含”某个元素
组合数的性质
完成这件事的类办法是相互独立的
“至多”或“至少”问题
有限制条件
建立恰当的分类标准,做到分类时不重不漏
的排列问题
分步
明确必须要经过几步才能完成这件事
注意几何问题本身的限制条件几何组合问题
无限制条件
的排列问题
完成事情分成若干个步骤,缺少哪一步,这件事都不可能完成
运用分类思想若干集合中选取元素问题
正确分步,逐步去做,步骤完整
非均匀不编号分组
C=C
反映了组合数的对称性,即从个元素中取出m
首先认真分析题意,看能否把问题归结为排列问题。如果是,然后用排列数公式求解
均匀不编号分组
分组问题常见形式
个元素与从n个元素中取出(n-m】个元素是相等的
非均匀编号分组
①有特殊元素或特殊位置;2元素必相邻:③元素不相邻:④元素有序限制
均匀编号分组
可理解为分类加法原理的应用:从(+1)
CCC
个元素中取出m个元素,可看做一类含有某
解题策略
1特殊元素(位置),优先考虑;2.不相邻问题,插空排;3相邻问题,捆绑处理;
遵箭先分组,后排列的原分配问题的处理途径
一元素,一类不含某一元素
4多元问题,分类讨论:5当正面求解比较困难时,可以用“间接法”
同课章节目录
