导数及其应用课件-2022届高三数学二轮专题复习(30张PPT)
文档属性
| 名称 | 导数及其应用课件-2022届高三数学二轮专题复习(30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 575.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 16:13:49 | ||
图片预览










文档简介
(共30张PPT)
导数及其应用
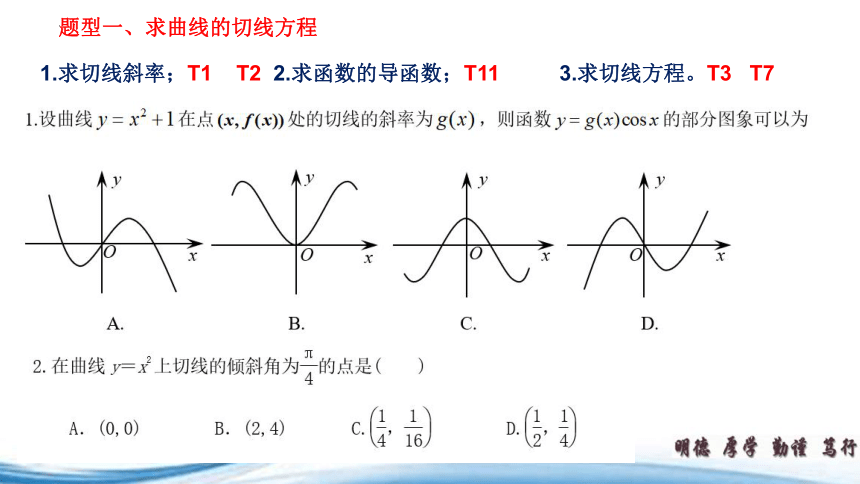
题型一、求曲线的切线方程
1.求切线斜率;T1 T2 2.求函数的导函数;T11 3.求切线方程。T3 T7
题型一、求曲线的切线方程
1.求切线斜率;T1 T2 2.求函数的导函数;T11 3.求切线方程。T3
题型一、求曲线的切线方程
1.求函数的导函数;T11 2.求切线斜率;T1 T2 3.求切线方程。T3
注:①已知点是否在曲线上,决定了它是否是切点,若不是,首先设出切点坐标,接着才能表示切线斜率。
题型二、求函数的单调性问题 T16 T17
1.求定义域;
2.求导;
3.令
.画草图列表(利用导数建立不等式);
5.求出函数单调区间。
题型二、求函数的单调性问题 T16 T17
1.求定义域;
2.求导;
3.令
.画草图列表(利用导数建立不等式);
5.求出函数单调区间。
注:①定义域优先;②注意单调区间是否可以开闭;③零点存在但求不出来就是隐零点问题,这类问题我们一般采用设而不求,通过整体代换和过渡,再结合其他条件,从而使问题得到解决。
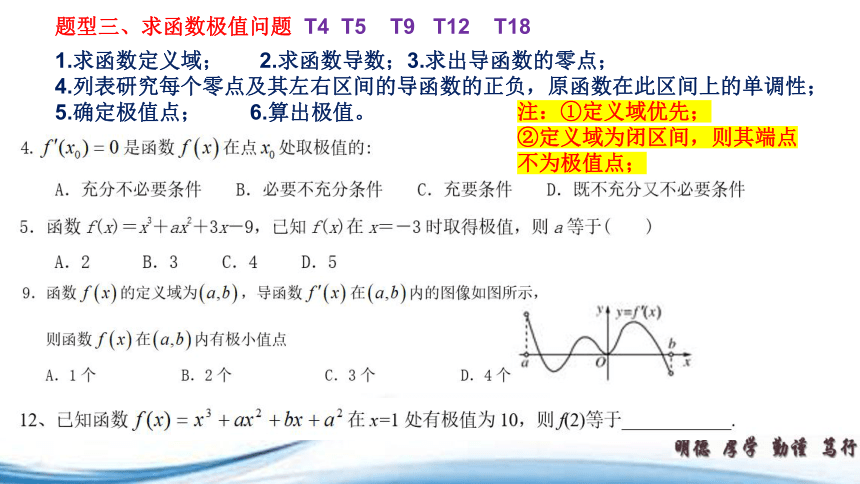
题型三、求函数极值问题 T4 T5 T9 T12 T18
1.求函数定义域; 2.求函数导数;3.求出导函数的零点;
4.列表研究每个零点及其左右区间的导函数的正负,原函数在此区间上的单调性;5.确定极值点; 6.算出极值。
注:①定义域优先;
②定义域为闭区间,则其端点不为极值点;
题型三、求函数极值问题 T4 T5 T9 T12 T18
题型四、求函数最值问题 T13
1.求函数的极值(有列表);
2.在上表两端加上端点的函数值;
3.比较极大值与端点的值求出最大值;
4.比较极小值与端点的值求出最小值;
注:在定义域内只有一个极值,则其就为最值。
题型五、已知极值点或极值求参数问题 T14
注:①导数为0的点是其为极值点的必要不充分条件;②检验。
1.求函数导数;
2.代入极值点建立方程 ;
3.求出参数;
4.检验所求参数值是否符合题意。
题型六、已知单调性求参数问题 T6 T8
1.求函数定义域;2.求函数导数;3.构造恒成立的不等式;
4.构造含参数的新函数或分离参数后构造新函数;
5.对新构造函数求导,讨论其最值;6.得出结论。
题型六、已知单调性求参数问题 T6 T8
1.求函数定义域;2.求函数导数;3.构造恒成立的不等式;
4.构造含参数的新函数或分离参数后构造新函数;
5.对新构造函数求导,讨论其最值;6.得出结论。
注:①定义域优先;构造恒成立的不等式要加等号;
②一阶导数不能解决问题,可研究二阶导数。
题型七、构造函数求不等式的解集问题 T15
构造一、基础构造型
构造二、次幂型
构造三、指数、对数型
题型七、构造函数求不等式的解集问题 T15
构造一、基础构造型
构造二、次幂型
构造三、指数、对数型
题型七、构造函数求不等式的解集问题 T15
题型八、导数与基本不等式相结合问题 T10
题型九、三次函数的图像与性质
导数及其应用
题型一、求曲线的切线方程
1.求切线斜率;T1 T2 2.求函数的导函数;T11 3.求切线方程。T3 T7
题型一、求曲线的切线方程
1.求切线斜率;T1 T2 2.求函数的导函数;T11 3.求切线方程。T3
题型一、求曲线的切线方程
1.求函数的导函数;T11 2.求切线斜率;T1 T2 3.求切线方程。T3
注:①已知点是否在曲线上,决定了它是否是切点,若不是,首先设出切点坐标,接着才能表示切线斜率。
题型二、求函数的单调性问题 T16 T17
1.求定义域;
2.求导;
3.令
.画草图列表(利用导数建立不等式);
5.求出函数单调区间。
题型二、求函数的单调性问题 T16 T17
1.求定义域;
2.求导;
3.令
.画草图列表(利用导数建立不等式);
5.求出函数单调区间。
注:①定义域优先;②注意单调区间是否可以开闭;③零点存在但求不出来就是隐零点问题,这类问题我们一般采用设而不求,通过整体代换和过渡,再结合其他条件,从而使问题得到解决。
题型三、求函数极值问题 T4 T5 T9 T12 T18
1.求函数定义域; 2.求函数导数;3.求出导函数的零点;
4.列表研究每个零点及其左右区间的导函数的正负,原函数在此区间上的单调性;5.确定极值点; 6.算出极值。
注:①定义域优先;
②定义域为闭区间,则其端点不为极值点;
题型三、求函数极值问题 T4 T5 T9 T12 T18
题型四、求函数最值问题 T13
1.求函数的极值(有列表);
2.在上表两端加上端点的函数值;
3.比较极大值与端点的值求出最大值;
4.比较极小值与端点的值求出最小值;
注:在定义域内只有一个极值,则其就为最值。
题型五、已知极值点或极值求参数问题 T14
注:①导数为0的点是其为极值点的必要不充分条件;②检验。
1.求函数导数;
2.代入极值点建立方程 ;
3.求出参数;
4.检验所求参数值是否符合题意。
题型六、已知单调性求参数问题 T6 T8
1.求函数定义域;2.求函数导数;3.构造恒成立的不等式;
4.构造含参数的新函数或分离参数后构造新函数;
5.对新构造函数求导,讨论其最值;6.得出结论。
题型六、已知单调性求参数问题 T6 T8
1.求函数定义域;2.求函数导数;3.构造恒成立的不等式;
4.构造含参数的新函数或分离参数后构造新函数;
5.对新构造函数求导,讨论其最值;6.得出结论。
注:①定义域优先;构造恒成立的不等式要加等号;
②一阶导数不能解决问题,可研究二阶导数。
题型七、构造函数求不等式的解集问题 T15
构造一、基础构造型
构造二、次幂型
构造三、指数、对数型
题型七、构造函数求不等式的解集问题 T15
构造一、基础构造型
构造二、次幂型
构造三、指数、对数型
题型七、构造函数求不等式的解集问题 T15
题型八、导数与基本不等式相结合问题 T10
题型九、三次函数的图像与性质
同课章节目录
