山东省聊城市重点中学2012-2013学年高一上学期第四次模块检测数学试题
文档属性
| 名称 | 山东省聊城市重点中学2012-2013学年高一上学期第四次模块检测数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 126.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-17 14:57:51 | ||
图片预览



文档简介
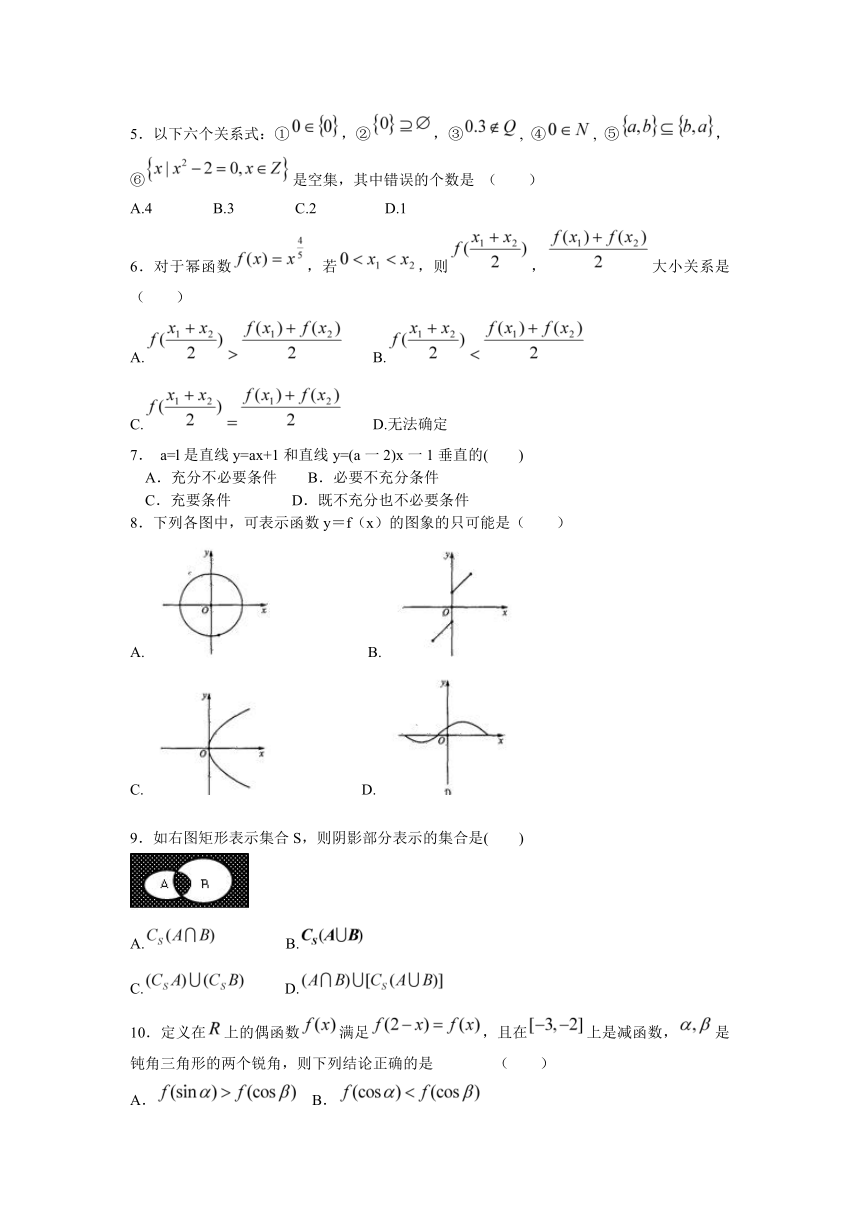
山东省聊城市某重点中学2012-2013学年高一上学期第四次模块检测数学试题
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
评卷人
得分
一、选择题
1.设集合S={},在S上定义运算为:=Ak,其中k为i+j被4除的余数,i、j=0,1,2,3.满足关系式的x(x∈S)的个数为( )
A.4 B.3 C.2 D.1
2.设集合则下列图形中能表示A与B关系的是( )
A. B.
C. D.
3.若函数 一定是 ( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
4.在正三棱柱( )
A. B. C. D.
5.以下六个关系式:①,②,③, ④, ⑤,⑥是空集,其中错误的个数是 ( )
A.4 B.3 C.2 D.1
6.对于幂函数,若,则,大小关系是( )
A. B.
C. D.无法确定
7. a=l是直线y=ax+1和直线y=(a一2)x一1垂直的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.下列各图中,可表示函数y=f(x)的图象的只可能是( )
A. B.
C. D.
9.如右图矩形表示集合S,则阴影部分表示的集合是( )
A. B.
C. D.
10.定义在上的偶函数满足,且在上是减函数,是钝角三角形的两个锐角,则下列结论正确的是 ( )
A. B.
C. D.
11.已知函数f(x)(xR)为奇函数, f(2)=1, f(x+2)=f(x)+f(2),则f(3)等于( )
A. B.1 C. D. 2
12.已知奇函数f(x)列任意的正实数x1,x2(x1≠x2),恒有( )
(x1-x2)( (x1)-f(x2)>0),则一定正确的是
A.f(4)>f(一6) B.f(一4) C.f(一4)>f(一6)D.f(4)第II卷(非选择题)
评卷人
得分
二、填空题
13.化简的结果是 .
14.设P是一个数集,且至少含有两个数,若对任意,都有(除数),则称P是一个数域.例如有理数集Q是数域;数集也是数域.有下列命题:
①整数集是数域; ②若有理数集,则数集M必为数域;
③数域必为无限集; ④存在无穷多个数域.
其中正确的命题的序号是 .(把你认为正确的命题的序号填填上)
15.函数的反函数
16.设函数,若关于的方程在上恰好有两个相异实根,则实数的取值范围为______________.
评卷人
得分
三、解答题
17.已知函数是偶函数.
(1) 求的值;
(2) 设,若函数与的图象有且只有一个公共点,求实数的取值范围.
18.已知函数
(1)若在上单调递增,求的取值范围;
(2)若定义在区间D上的函数对于区间上的任意两个值总有以下
不等式成立,则称函数为区间上的
“凹函数”.试证当时,为“凹函数”.
19.求斜率为,且与坐标轴所围成的三角形的周长是12的直线的方程。
20.某商家有一种商品,成本费为a 元,如果月初售出可获利100元,再将本利都存入银行,已知银行月息为2.4%,如果月末售出可获利120元,但要付保管费5元,试就 a的取值说明这种商品是月初售出好,还是月末售出好?
21.已知△BCD中,∠BCD=,BC=CD=1,AB⊥平面BCD,
∠ADB=,E、F分别是AC、AD上的动点,且
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD ?
高一数学参考答案
一、选择题
1.C??????
解析:由定义能满足关系式,同理x=A3满足关系式
2.A??????3.A??????4.B??????5.C??????6.A??????7.C??????
解析:若a=1,则直线y=x+1和直线y=-x-1的斜率乘积为一1,所以两者互相垂直;若直线y=ax+1和直线y=(a一2)x—1垂直,则有a(a一2)=一1,解之得a=1.故为充要条件
8.D??????9.D??????10.D??????
解析:由可知图象关于对称,又因为为偶函数图象关于对称,可得到为周期函数且最小正周期为2,结合在区间上是减函数,画出满足题意的一个函数图象如右图所示.因为是钝角三角形的两个锐角,所以,,所以, 所以.
11.C??????
该题考查抽象函数的性质,由于=+,代入x=1,显然=+=一f(1)+1=,则==+ = 12. C?
解析:该题考查抽象函数的运算,显然(4—6)(一))>0<,结合奇函数的定义,得—=,一=,故>
二、填空题
12.
13.③④
14.
15.
三、解答题
16.解:(1) ∵ 函数是偶函数 ????????????? ∴ ????????????? 恒成立 ????????????? ∴ ,则 ????????????? (2) , ????????????? 函数与的图象有且只有一个公共点,即 ????????????? 方程只有一个解????????????? ????????????? 由已知得: ????????????? ∴ ????????????? 方程等价于: ????????????? 设,则有一解 ????????????? 若,设,∵,∴恰好有一正解 ????????????? ∴ 满足题意 ????????????? 若,即时,不满足题意 ????????????? 若,即时,由,得或 ????????????? 当时,满足题意 ????????????? 当时,(舍去) ????????????? 综上所述:实数的取值范围是
17.解(1)由,得 函数为上单调函数. 若函数为上单调增函数,则在上恒成立,即不等式在上恒成立. 也即在上恒成立. 令,上述问题等价于,而为在上的减函数,则,于是为所求. (2)证明:由 得 ? ?? 而? ① ??? 又,? ∴? ② ∵?? ∴, ∵? ∴? ③? 由①、②、③得 即,从而由凹函数的定义可知函数为凹函数
18.解:设直线l的方程为,令,令,,解得, 所求的直线方程为。
19.解:由已知商品的成本费为a元,则若月初售出,到月末共获利润为: =100+(a+100)×2.4% =0.024 a+102.4??????????? 若月末售出,可获利=120-5=115(元) -=0.024a-12.6=0.024(a-525) 故当成本a大于525元时,月初售出好; 当成本a小于525元时,月末售出好; 当成本a等于525元时,月初、月末售出获利相同
20.证明:(Ⅰ)∵AB⊥平面BCD, ∴AB⊥CD, ????????????? ∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC.? ????????????? 又 ????????????? ∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF平面BEF, ????????????? ∴不论λ为何值恒有平面BEF⊥平面ABC. (Ⅱ)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD, ∴BE⊥平面ACD,∴BE⊥AC. ∵BC=CD=1,∠BCD=,∠ADB=, ∴ 由得 故当时,平面BEF⊥平面ACD.
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
评卷人
得分
一、选择题
1.设集合S={},在S上定义运算为:=Ak,其中k为i+j被4除的余数,i、j=0,1,2,3.满足关系式的x(x∈S)的个数为( )
A.4 B.3 C.2 D.1
2.设集合则下列图形中能表示A与B关系的是( )
A. B.
C. D.
3.若函数 一定是 ( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
4.在正三棱柱( )
A. B. C. D.
5.以下六个关系式:①,②,③, ④, ⑤,⑥是空集,其中错误的个数是 ( )
A.4 B.3 C.2 D.1
6.对于幂函数,若,则,大小关系是( )
A. B.
C. D.无法确定
7. a=l是直线y=ax+1和直线y=(a一2)x一1垂直的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.下列各图中,可表示函数y=f(x)的图象的只可能是( )
A. B.
C. D.
9.如右图矩形表示集合S,则阴影部分表示的集合是( )
A. B.
C. D.
10.定义在上的偶函数满足,且在上是减函数,是钝角三角形的两个锐角,则下列结论正确的是 ( )
A. B.
C. D.
11.已知函数f(x)(xR)为奇函数, f(2)=1, f(x+2)=f(x)+f(2),则f(3)等于( )
A. B.1 C. D. 2
12.已知奇函数f(x)列任意的正实数x1,x2(x1≠x2),恒有( )
(x1-x2)( (x1)-f(x2)>0),则一定正确的是
A.f(4)>f(一6) B.f(一4)
评卷人
得分
二、填空题
13.化简的结果是 .
14.设P是一个数集,且至少含有两个数,若对任意,都有(除数),则称P是一个数域.例如有理数集Q是数域;数集也是数域.有下列命题:
①整数集是数域; ②若有理数集,则数集M必为数域;
③数域必为无限集; ④存在无穷多个数域.
其中正确的命题的序号是 .(把你认为正确的命题的序号填填上)
15.函数的反函数
16.设函数,若关于的方程在上恰好有两个相异实根,则实数的取值范围为______________.
评卷人
得分
三、解答题
17.已知函数是偶函数.
(1) 求的值;
(2) 设,若函数与的图象有且只有一个公共点,求实数的取值范围.
18.已知函数
(1)若在上单调递增,求的取值范围;
(2)若定义在区间D上的函数对于区间上的任意两个值总有以下
不等式成立,则称函数为区间上的
“凹函数”.试证当时,为“凹函数”.
19.求斜率为,且与坐标轴所围成的三角形的周长是12的直线的方程。
20.某商家有一种商品,成本费为a 元,如果月初售出可获利100元,再将本利都存入银行,已知银行月息为2.4%,如果月末售出可获利120元,但要付保管费5元,试就 a的取值说明这种商品是月初售出好,还是月末售出好?
21.已知△BCD中,∠BCD=,BC=CD=1,AB⊥平面BCD,
∠ADB=,E、F分别是AC、AD上的动点,且
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD ?
高一数学参考答案
一、选择题
1.C??????
解析:由定义能满足关系式,同理x=A3满足关系式
2.A??????3.A??????4.B??????5.C??????6.A??????7.C??????
解析:若a=1,则直线y=x+1和直线y=-x-1的斜率乘积为一1,所以两者互相垂直;若直线y=ax+1和直线y=(a一2)x—1垂直,则有a(a一2)=一1,解之得a=1.故为充要条件
8.D??????9.D??????10.D??????
解析:由可知图象关于对称,又因为为偶函数图象关于对称,可得到为周期函数且最小正周期为2,结合在区间上是减函数,画出满足题意的一个函数图象如右图所示.因为是钝角三角形的两个锐角,所以,,所以, 所以.
11.C??????
该题考查抽象函数的性质,由于=+,代入x=1,显然=+=一f(1)+1=,则==+ = 12. C?
解析:该题考查抽象函数的运算,显然(4—6)(一))>0<,结合奇函数的定义,得—=,一=,故>
二、填空题
12.
13.③④
14.
15.
三、解答题
16.解:(1) ∵ 函数是偶函数 ????????????? ∴ ????????????? 恒成立 ????????????? ∴ ,则 ????????????? (2) , ????????????? 函数与的图象有且只有一个公共点,即 ????????????? 方程只有一个解????????????? ????????????? 由已知得: ????????????? ∴ ????????????? 方程等价于: ????????????? 设,则有一解 ????????????? 若,设,∵,∴恰好有一正解 ????????????? ∴ 满足题意 ????????????? 若,即时,不满足题意 ????????????? 若,即时,由,得或 ????????????? 当时,满足题意 ????????????? 当时,(舍去) ????????????? 综上所述:实数的取值范围是
17.解(1)由,得 函数为上单调函数. 若函数为上单调增函数,则在上恒成立,即不等式在上恒成立. 也即在上恒成立. 令,上述问题等价于,而为在上的减函数,则,于是为所求. (2)证明:由 得 ? ?? 而? ① ??? 又,? ∴? ② ∵?? ∴, ∵? ∴? ③? 由①、②、③得 即,从而由凹函数的定义可知函数为凹函数
18.解:设直线l的方程为,令,令,,解得, 所求的直线方程为。
19.解:由已知商品的成本费为a元,则若月初售出,到月末共获利润为: =100+(a+100)×2.4% =0.024 a+102.4??????????? 若月末售出,可获利=120-5=115(元) -=0.024a-12.6=0.024(a-525) 故当成本a大于525元时,月初售出好; 当成本a小于525元时,月末售出好; 当成本a等于525元时,月初、月末售出获利相同
20.证明:(Ⅰ)∵AB⊥平面BCD, ∴AB⊥CD, ????????????? ∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC.? ????????????? 又 ????????????? ∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF平面BEF, ????????????? ∴不论λ为何值恒有平面BEF⊥平面ABC. (Ⅱ)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD, ∴BE⊥平面ACD,∴BE⊥AC. ∵BC=CD=1,∠BCD=,∠ADB=, ∴ 由得 故当时,平面BEF⊥平面ACD.
同课章节目录
