2022届高三数学二轮复习:空间几何体的表面积和体积 课件(32张PPT)
文档属性
| 名称 | 2022届高三数学二轮复习:空间几何体的表面积和体积 课件(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 16:31:56 | ||
图片预览










文档简介
(共32张PPT)
2022届高三数学二轮复习备考
—空间几何体的表面积和体积
一、形成知识网络,强化知识点,重视边缘知识;
二、注重通性通法,找到增分点,提高运算能力。
三、加强书写表达训练,规范答题步骤,向步骤要分;
教学目标
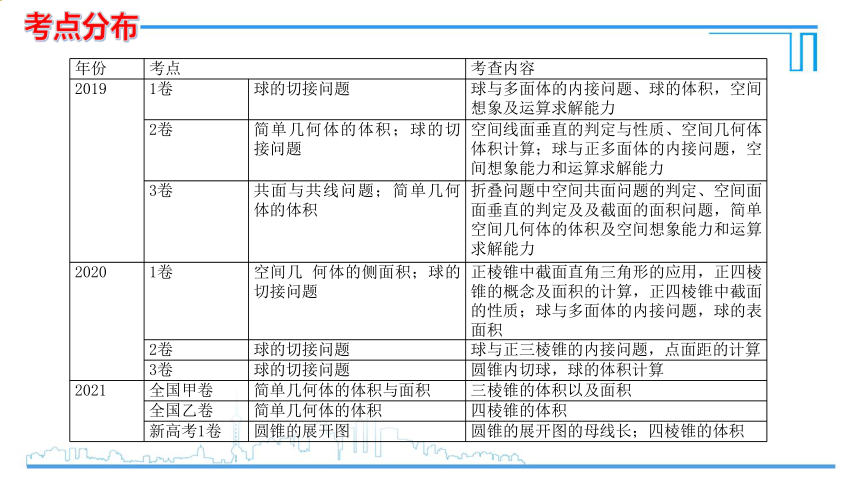
考点分布
年份 考点 考查内容
2019 1卷 球的切接问题 球与多面体的内接问题、球的体积,空间想象及运算求解能力
2卷 简单几何体的体积;球的切接问题 空间线面垂直的判定与性质、空间几何体体积计算;球与正多面体的内接问题,空间想象能力和运算求解能力
3卷 共面与共线问题;简单几何体的体积 折叠问题中空间共面问题的判定、空间面面垂直的判定及及截面的面积问题,简单空间几何体的体积及空间想象能力和运算求解能力
2020 1卷 空间几 何体的侧面积;球的切接问题 正棱锥中截面直角三角形的应用,正四棱锥的概念及面积的计算,正四棱锥中截面的性质;球与多面体的内接问题,球的表面积
2卷 球的切接问题 球与正三棱锥的内接问题,点面距的计算
3卷 球的切接问题 圆锥内切球,球的体积计算
2021 全国甲卷 简单几何体的体积与面积 三棱锥的体积以及面积
全国乙卷 简单几何体的体积 四棱锥的体积
新高考1卷 圆锥的展开图 圆锥的展开图的母线长;四棱锥的体积
空间几何体的结构特征是立体几何的基础,空间几何体的表面积与体积是高考题的重点与热点,保持“一小一大”或“两小一大”的格局,多以选择题或者填空题的形式考查空间几何体的体积或表面积的计算,或是与球有关的相接、相切计算问题,属于中等难度.
1.空间几何体分为多面体和旋转体
研究其特性常采用化空间为平面的方法,如截面图、轴截面等.
2.旋转体的表面积和体积公式
(1)S圆柱侧=2πrl,S圆锥侧=πrl,S圆台侧=π(r1+r2)l,S球=4πR2 ,V柱=sh,V锥=sh,V球=πR3.
(2)球的截面的性质:用一个平面去截球,截面是圆面;球心和截面圆的距离d与球的半径R及截面圆半径r之间的关系是r= .
要点整合
3.空间几何体的体积与表面积求法
(1)割补法:求不规则几何体的体积或表面积时,通过割补,转化成规则几何体求解.
(2)等积变换:涉及三棱锥的体积,注意灵活选择底面和对应的高.
4.多面体与球
(1)当球内切于正方体时,球的直径等于正方体的棱长,当球外接于长方体时,长方体的体对角线长等于球的直径;
当球与正方体各棱都相切时,球的直径等于正方体底面的对角线长.
(2)若正四面体的棱长为a,则正四面体的外接球半径为a,内切球半径为a.
要点整合
真题再现
B
D
A
题型探究
【题型一】空间几何体的展开图、截面图
对点训练
A
B
对点训练
题型探究
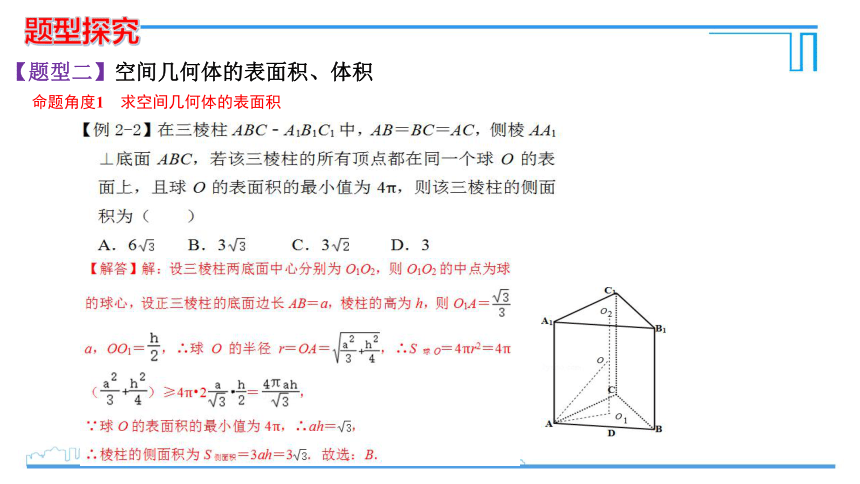
【题型二】空间几何体的表面积、体积
命题角度1 求空间几何体的表面积
题型探究
【题型二】空间几何体的表面积、体积
命题角度1 求空间几何体的表面积
求几何体的表面积的方法
(1)求表面积问题的基本思路是将立体几何问题转化为平面几何问题,
即空间图形平面化,这是解决立体几何的主要出发点.
(2)求不规则几何体的表面积时,通常将所给几何体分割成基本的柱、
锥、台体,先求这些柱、锥、台体的表面积,再通过求和或作差得不规则
几何体的表面积.
规律方法
对点训练
1、将一个斜边长为4的等腰直角三角形以其一直角边所在直线为旋转轴旋转一周,所得几何体 的表面积为_________.
2、(2022·广东省广州市10月调研)若圆台的上,下底面半径分别为2,4,高为2,则该圆台的侧面积为______.
题型探究
【题型二】空间几何体的表面积、体积
命题角度2 求空间几何体的体积
解析 设圆锥的底面半径为r,母线长为l,高为h,因为圆锥的轴截面是等腰直
A
题型探究
【题型二】空间几何体的表面积、体积
命题角度2 求空间几何体的体积
【例3-2】(2021·山东泰安市·高三其他模拟)如图是我国古代米斗,它是称量粮食的量器,是古代官仓、粮栈、米行等必备的用具.它是随着粮食生产而发展出来的用具,早在先秦时期就有,到秦代统一了度量衡,汉代又进一步制度化,十升为斗、十斗为石的标准最终确定下来.若将某个米斗近似看作一个四棱台,上、下两个底面都是正方形,侧棱均相等,上底面边长为25CM ,下底面边长为15CM ,侧棱长为10CM ,则该米斗的容积约为( )
附:
题型探究
规律方法
求几何体体积的基本方法
(1)直接法:对于规则的几何体,可利用相关公式直接计算求解.
(2)割补法:对于不规则的几何体,可将其分割成规则的几何体,进行体积计算;也可把不规则的几何体补成规则的几何体,进行体积计算.
(3)转换法:主要用于求三棱锥(四面体)的体积,将三棱锥的顶点和底面进行转换,使其底面的面积可求(或容易求),高可求(或容易求),从而代入公式求得体积.
对点训练
对点训练
对点训练
3.(2021·遵义市第十八中学高三模拟)如图,在正三棱柱ABC A1B1C1中,已知AB=AA1=3,点P在棱CC1上,则三棱锥P ABA1的体积为________.
对点训练
4.(2021·广州调研)在四面体ABCD中,已知AD=DB=AC=CB=1,则该四面体的体积的最大值为__________.
题型探究
【题型三】与球有关的切接问题
【例4—1】 (2020·高考全国卷Ⅰ)已知A,B,C为球O的球面上的三个点,⊙O1为 △ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )
A.64π B.48π C.36π D.32π
【解析】如图所示,设球O的半径为R,⊙O1的半径为r,因为⊙O1的面积为4π,所以4π=πr2,解得r=2,
又AB=BC=AC=OO1,所以=2r,解得AB=2,故OO1=2,所以R2=OO+r2=(2)2+22=16,
所以球O的表面积S=4πR2=64π.故选A.
题型探究
【题型三】与球有关的切接问题
题型探究
【题型三】与球有关的切接问题
[例4-3](2021·广东深圳二模)若在母线长为5,高为4的圆锥中挖去一个小球,则剩余部分的体积的最小值为 .
规律方法
解决与球有关的切、接问题的策略
1.解决多面体的外接球问题,关键是确定球心的位置,方法是先选择多面体的一面,确定此面外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置.对于特殊的多面体还可以采用补成正方体或者长方体的方法找到球心的位置.
2.求解多面体的内切球问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各棱锥的体积之和求内切球的半径.
对点训练
1.(2021·山东泰安一模)已知三棱柱的侧棱垂直于底面,所有棱长都为1,顶点都在一个球面上,则该球的表面积为( )
对点训练
对点训练
对点训练
3.(圆柱的外接球)将一个表面积为100π的木质球削成一个体积最大的圆柱,则该圆柱的高为________.
对点训练
4.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.
对点训练
2022届高三数学二轮复习备考
—空间几何体的表面积和体积
一、形成知识网络,强化知识点,重视边缘知识;
二、注重通性通法,找到增分点,提高运算能力。
三、加强书写表达训练,规范答题步骤,向步骤要分;
教学目标
考点分布
年份 考点 考查内容
2019 1卷 球的切接问题 球与多面体的内接问题、球的体积,空间想象及运算求解能力
2卷 简单几何体的体积;球的切接问题 空间线面垂直的判定与性质、空间几何体体积计算;球与正多面体的内接问题,空间想象能力和运算求解能力
3卷 共面与共线问题;简单几何体的体积 折叠问题中空间共面问题的判定、空间面面垂直的判定及及截面的面积问题,简单空间几何体的体积及空间想象能力和运算求解能力
2020 1卷 空间几 何体的侧面积;球的切接问题 正棱锥中截面直角三角形的应用,正四棱锥的概念及面积的计算,正四棱锥中截面的性质;球与多面体的内接问题,球的表面积
2卷 球的切接问题 球与正三棱锥的内接问题,点面距的计算
3卷 球的切接问题 圆锥内切球,球的体积计算
2021 全国甲卷 简单几何体的体积与面积 三棱锥的体积以及面积
全国乙卷 简单几何体的体积 四棱锥的体积
新高考1卷 圆锥的展开图 圆锥的展开图的母线长;四棱锥的体积
空间几何体的结构特征是立体几何的基础,空间几何体的表面积与体积是高考题的重点与热点,保持“一小一大”或“两小一大”的格局,多以选择题或者填空题的形式考查空间几何体的体积或表面积的计算,或是与球有关的相接、相切计算问题,属于中等难度.
1.空间几何体分为多面体和旋转体
研究其特性常采用化空间为平面的方法,如截面图、轴截面等.
2.旋转体的表面积和体积公式
(1)S圆柱侧=2πrl,S圆锥侧=πrl,S圆台侧=π(r1+r2)l,S球=4πR2 ,V柱=sh,V锥=sh,V球=πR3.
(2)球的截面的性质:用一个平面去截球,截面是圆面;球心和截面圆的距离d与球的半径R及截面圆半径r之间的关系是r= .
要点整合
3.空间几何体的体积与表面积求法
(1)割补法:求不规则几何体的体积或表面积时,通过割补,转化成规则几何体求解.
(2)等积变换:涉及三棱锥的体积,注意灵活选择底面和对应的高.
4.多面体与球
(1)当球内切于正方体时,球的直径等于正方体的棱长,当球外接于长方体时,长方体的体对角线长等于球的直径;
当球与正方体各棱都相切时,球的直径等于正方体底面的对角线长.
(2)若正四面体的棱长为a,则正四面体的外接球半径为a,内切球半径为a.
要点整合
真题再现
B
D
A
题型探究
【题型一】空间几何体的展开图、截面图
对点训练
A
B
对点训练
题型探究
【题型二】空间几何体的表面积、体积
命题角度1 求空间几何体的表面积
题型探究
【题型二】空间几何体的表面积、体积
命题角度1 求空间几何体的表面积
求几何体的表面积的方法
(1)求表面积问题的基本思路是将立体几何问题转化为平面几何问题,
即空间图形平面化,这是解决立体几何的主要出发点.
(2)求不规则几何体的表面积时,通常将所给几何体分割成基本的柱、
锥、台体,先求这些柱、锥、台体的表面积,再通过求和或作差得不规则
几何体的表面积.
规律方法
对点训练
1、将一个斜边长为4的等腰直角三角形以其一直角边所在直线为旋转轴旋转一周,所得几何体 的表面积为_________.
2、(2022·广东省广州市10月调研)若圆台的上,下底面半径分别为2,4,高为2,则该圆台的侧面积为______.
题型探究
【题型二】空间几何体的表面积、体积
命题角度2 求空间几何体的体积
解析 设圆锥的底面半径为r,母线长为l,高为h,因为圆锥的轴截面是等腰直
A
题型探究
【题型二】空间几何体的表面积、体积
命题角度2 求空间几何体的体积
【例3-2】(2021·山东泰安市·高三其他模拟)如图是我国古代米斗,它是称量粮食的量器,是古代官仓、粮栈、米行等必备的用具.它是随着粮食生产而发展出来的用具,早在先秦时期就有,到秦代统一了度量衡,汉代又进一步制度化,十升为斗、十斗为石的标准最终确定下来.若将某个米斗近似看作一个四棱台,上、下两个底面都是正方形,侧棱均相等,上底面边长为25CM ,下底面边长为15CM ,侧棱长为10CM ,则该米斗的容积约为( )
附:
题型探究
规律方法
求几何体体积的基本方法
(1)直接法:对于规则的几何体,可利用相关公式直接计算求解.
(2)割补法:对于不规则的几何体,可将其分割成规则的几何体,进行体积计算;也可把不规则的几何体补成规则的几何体,进行体积计算.
(3)转换法:主要用于求三棱锥(四面体)的体积,将三棱锥的顶点和底面进行转换,使其底面的面积可求(或容易求),高可求(或容易求),从而代入公式求得体积.
对点训练
对点训练
对点训练
3.(2021·遵义市第十八中学高三模拟)如图,在正三棱柱ABC A1B1C1中,已知AB=AA1=3,点P在棱CC1上,则三棱锥P ABA1的体积为________.
对点训练
4.(2021·广州调研)在四面体ABCD中,已知AD=DB=AC=CB=1,则该四面体的体积的最大值为__________.
题型探究
【题型三】与球有关的切接问题
【例4—1】 (2020·高考全国卷Ⅰ)已知A,B,C为球O的球面上的三个点,⊙O1为 △ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )
A.64π B.48π C.36π D.32π
【解析】如图所示,设球O的半径为R,⊙O1的半径为r,因为⊙O1的面积为4π,所以4π=πr2,解得r=2,
又AB=BC=AC=OO1,所以=2r,解得AB=2,故OO1=2,所以R2=OO+r2=(2)2+22=16,
所以球O的表面积S=4πR2=64π.故选A.
题型探究
【题型三】与球有关的切接问题
题型探究
【题型三】与球有关的切接问题
[例4-3](2021·广东深圳二模)若在母线长为5,高为4的圆锥中挖去一个小球,则剩余部分的体积的最小值为 .
规律方法
解决与球有关的切、接问题的策略
1.解决多面体的外接球问题,关键是确定球心的位置,方法是先选择多面体的一面,确定此面外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置.对于特殊的多面体还可以采用补成正方体或者长方体的方法找到球心的位置.
2.求解多面体的内切球问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各棱锥的体积之和求内切球的半径.
对点训练
1.(2021·山东泰安一模)已知三棱柱的侧棱垂直于底面,所有棱长都为1,顶点都在一个球面上,则该球的表面积为( )
对点训练
对点训练
对点训练
3.(圆柱的外接球)将一个表面积为100π的木质球削成一个体积最大的圆柱,则该圆柱的高为________.
对点训练
4.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.
对点训练
同课章节目录
