北京市朝阳区2012-2013学年高一上学期期末考试 数学Word版含答案
文档属性
| 名称 | 北京市朝阳区2012-2013学年高一上学期期末考试 数学Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-06 18:52:38 | ||
图片预览



文档简介
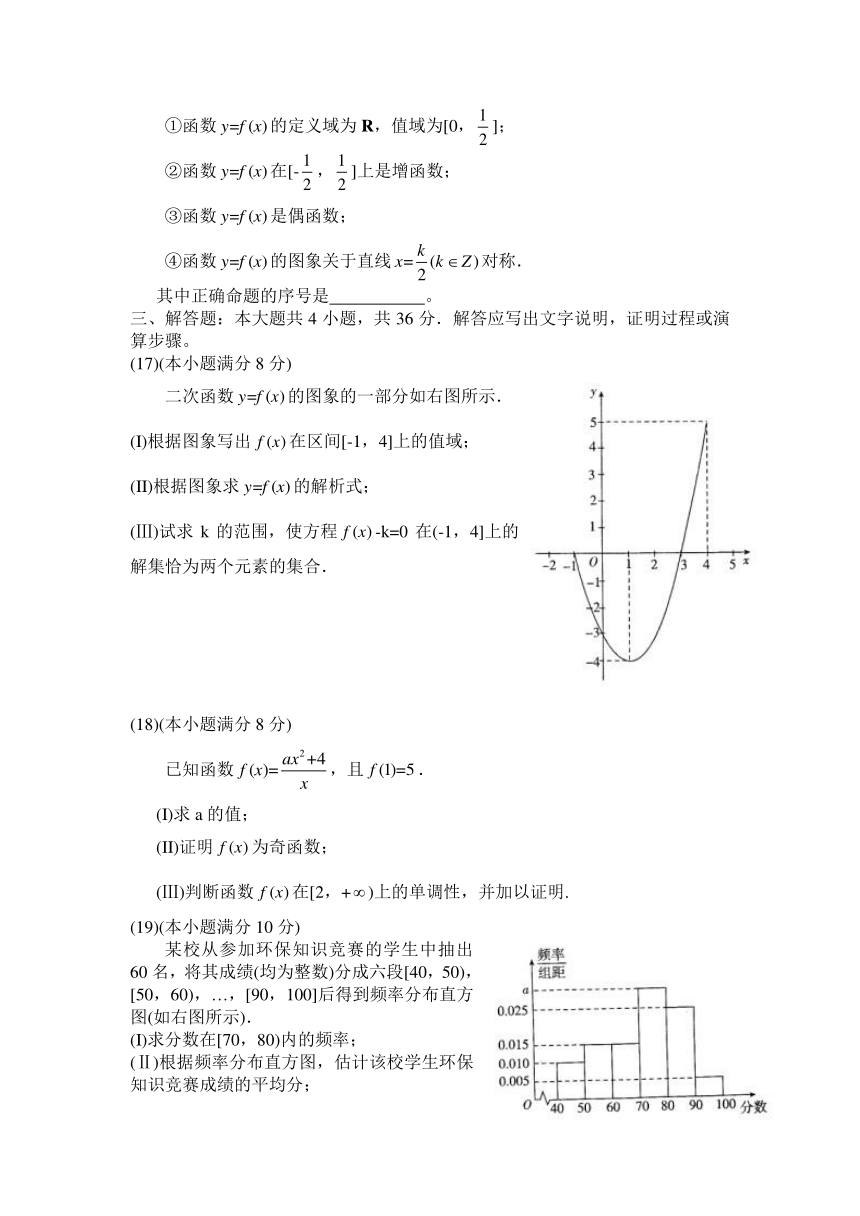
北京市朝阳区2012~2013学年度高一年级第一学期期末统一考试
数学试卷 2013.1
(考试时间l00分钟;卷面总分100分)
试题
选择题
填空题
(17)
(18)
(19)
(20)
总分
得分
一、选择题:本大题共l0小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
(1)设集合M={},N={},则MN等于
(A){} (B){}
(C){} (D){}
(2)当a>1时,在同一坐标系中,函数与的图象是
(3)右图是某赛季甲、乙两名篮球运动员每场比赛得分 的茎叶图,则甲、乙两人这几场比赛得分的中位数之 和是
(A)62 (B)63
(C)64 (D)65
(4)从1,2,3,4这4个数中,不放回地任意取两个数,两个数都是偶数的概率是
(A) (B) (C) (D)
(5)运行如图所示的程序框图,若输入n=4,则输出S的值为
(A)9 (B)10
(C)11 (D)12
(6)从装有2个红球和2个黑球的口袋内任取2个球,那么互斥 而不对立的两个事件是
(A)“至少有一个黑球”与“都是黑球”
(B)“至少有一个黑球”与“都是红球”
(C)“至少有一个黑球”与“至少有一个红球”
(D)“恰有一个黑球”与“恰有两个黑球”
(7)已知则的值为
(A)1 (B)2 (C)0 (D)-1
(8)根据表格中的数据,可以断定方程的一个根所在的区间是
-1
0
1
2
3
0.37
l
2.72
7.39
20.09
1
2
3
4
5
(A)(-1,0) (B)(0,1) (C)(1,2) (D) (2,3)
(9)如图所示,A是圆上一定点,在圆上其它位置任取一点A′,则弦AA′的长度大于等于半径长度的概率为
(A) (B)
(C) (D)
(10)设是(0,+∞)上的增函数,当时,,且,则
(A) (B)
(C) (D)
二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上.
(11)若幂函数的图象过点(2,),则= .
(12)某校高中部有三个年级,其中高三有学生1000人,现采用分层抽样法抽取一个容量为185的样本,已知抽取高一年级学生75人,抽取高二年级学生60人,则高中部共有学生的人数为 .
(13)函数的定义域是 .
(14)已知≠0,则函数的最大值是 .
(15)已知样本9,10,11,,的平均数是10,标准差是,则= .
(16)给出定义:若(其中m为整数),则m叫做离实数最近的整数,记作{}=m.在此基础上给出下列关于的函数的四个命题:
①函数的定义域为R,值域为[0,];
②函数在[-,]上是增函数;
③函数是偶函数;
④函数的图象关于直线对称.
其中正确命题的序号是 。
三、解答题:本大题共4小题,共36分.解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分8分)
二次函数的图象的一部分如右图所示.
(I)根据图象写出在区间[-1,4]上的值域;
(II)根据图象求的解析式;
(Ⅲ)试求k的范围,使方程-k=0在(-1,4]上的解集恰为两个元素的集合.
(18)(本小题满分8分)
已知函数,且.
(I)求a的值;
(II)证明为奇函数;
(Ⅲ)判断函数在[2,+)上的单调性,并加以证明.
(19)(本小题满分10分)
某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如右图所示).
(I)求分数在[70,80)内的频率;
(Ⅱ)根据频率分布直方图,估计该校学生环保知识竞赛成绩的平均分;
(Ⅲ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样 本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
(20)(本小题满分10分)
已知函数在区间[2,4]上的最大值为9,最小值为1,记.
(I)求实数a,b的值;
(Ⅱ)若不等式成立,求实数的取值范围;
(Ⅲ)定义在[p,q]上的函数,设将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式恒成立,则称函数为在[p,q]上的有界变差函数。试判 断函数是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.
(表示)
数学试卷 2013.1
(考试时间l00分钟;卷面总分100分)
试题
选择题
填空题
(17)
(18)
(19)
(20)
总分
得分
一、选择题:本大题共l0小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
(1)设集合M={},N={},则MN等于
(A){} (B){}
(C){} (D){}
(2)当a>1时,在同一坐标系中,函数与的图象是
(3)右图是某赛季甲、乙两名篮球运动员每场比赛得分 的茎叶图,则甲、乙两人这几场比赛得分的中位数之 和是
(A)62 (B)63
(C)64 (D)65
(4)从1,2,3,4这4个数中,不放回地任意取两个数,两个数都是偶数的概率是
(A) (B) (C) (D)
(5)运行如图所示的程序框图,若输入n=4,则输出S的值为
(A)9 (B)10
(C)11 (D)12
(6)从装有2个红球和2个黑球的口袋内任取2个球,那么互斥 而不对立的两个事件是
(A)“至少有一个黑球”与“都是黑球”
(B)“至少有一个黑球”与“都是红球”
(C)“至少有一个黑球”与“至少有一个红球”
(D)“恰有一个黑球”与“恰有两个黑球”
(7)已知则的值为
(A)1 (B)2 (C)0 (D)-1
(8)根据表格中的数据,可以断定方程的一个根所在的区间是
-1
0
1
2
3
0.37
l
2.72
7.39
20.09
1
2
3
4
5
(A)(-1,0) (B)(0,1) (C)(1,2) (D) (2,3)
(9)如图所示,A是圆上一定点,在圆上其它位置任取一点A′,则弦AA′的长度大于等于半径长度的概率为
(A) (B)
(C) (D)
(10)设是(0,+∞)上的增函数,当时,,且,则
(A) (B)
(C) (D)
二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上.
(11)若幂函数的图象过点(2,),则= .
(12)某校高中部有三个年级,其中高三有学生1000人,现采用分层抽样法抽取一个容量为185的样本,已知抽取高一年级学生75人,抽取高二年级学生60人,则高中部共有学生的人数为 .
(13)函数的定义域是 .
(14)已知≠0,则函数的最大值是 .
(15)已知样本9,10,11,,的平均数是10,标准差是,则= .
(16)给出定义:若(其中m为整数),则m叫做离实数最近的整数,记作{}=m.在此基础上给出下列关于的函数的四个命题:
①函数的定义域为R,值域为[0,];
②函数在[-,]上是增函数;
③函数是偶函数;
④函数的图象关于直线对称.
其中正确命题的序号是 。
三、解答题:本大题共4小题,共36分.解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分8分)
二次函数的图象的一部分如右图所示.
(I)根据图象写出在区间[-1,4]上的值域;
(II)根据图象求的解析式;
(Ⅲ)试求k的范围,使方程-k=0在(-1,4]上的解集恰为两个元素的集合.
(18)(本小题满分8分)
已知函数,且.
(I)求a的值;
(II)证明为奇函数;
(Ⅲ)判断函数在[2,+)上的单调性,并加以证明.
(19)(本小题满分10分)
某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如右图所示).
(I)求分数在[70,80)内的频率;
(Ⅱ)根据频率分布直方图,估计该校学生环保知识竞赛成绩的平均分;
(Ⅲ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样 本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
(20)(本小题满分10分)
已知函数在区间[2,4]上的最大值为9,最小值为1,记.
(I)求实数a,b的值;
(Ⅱ)若不等式成立,求实数的取值范围;
(Ⅲ)定义在[p,q]上的函数,设将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式恒成立,则称函数为在[p,q]上的有界变差函数。试判 断函数是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.
(表示)
同课章节目录
