平面向量的综合应用 课件(共23张PPT)
文档属性
| 名称 | 平面向量的综合应用 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 16:59:18 | ||
图片预览







文档简介
(共23张PPT)
《平面向量的综合应用一》
热身训练
设分别是的三边线段上的点,且,则与( )
解:
反向平行 同向平行 互相垂直 既不平行也不垂直
无序 → 有序
基底
转化
平面向量综合应用中的基底策略
温故知新:
平面向量的基本定理
/ 01
温故知新
平面向量基本定理
如果、 是同一平面内的两个________向量,那么对于这一平面内的任意向量___________ 一对实数、,使得,其中、 称为一组_________.
填一填:
不共线
有且仅有
基底
温故知新
例1 在中,是线段的三等分点,则的值为.
问题1:利用基底法解决平面向量问题的基本步骤是什么?
基底法一般步骤:
①在平面图形中选取两个不共线向量;
②把问题中涉及的向量用进行线性表示;
③利用向量的运算法则和性质求解.
解:
未知 → 已知
基底
转化
课堂探究:
平面向量综合应用中的
基底策略
/ 02
课堂探究
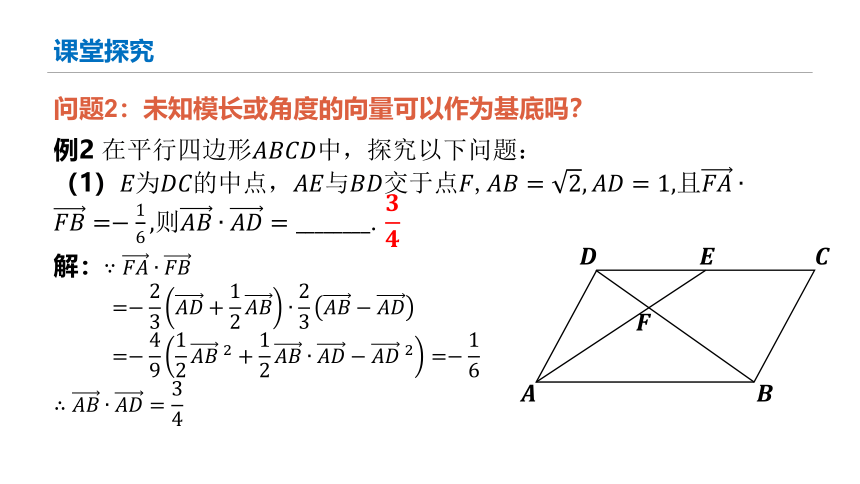
例2 在平行四边形中,探究以下问题:
(1)为的中点,与交于点,且则.
问题2:未知模长或角度的向量可以作为基底吗?
解:
课堂探究
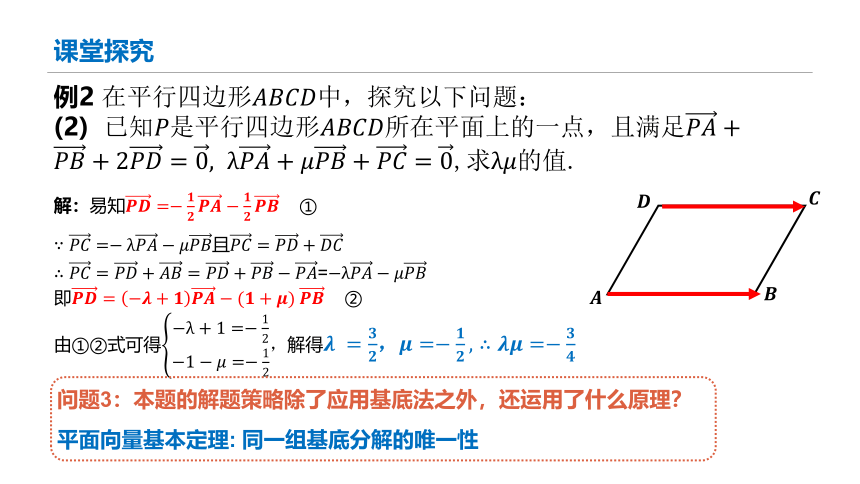
例2 在平行四边形中,探究以下问题:
(2) 已知是平行四边形所在平面上的一点,且满足 ,求的值.
问题3:本题的解题策略除了应用基底法之外,还运用了什么原理?
解:易知 ①
且
=
即 ②
由①②式可得解得,
平面向量基本定理: 同一组基底分解的唯一性
课堂探究
例2 在平行四边形中,探究以下问题:
(3) 分别是线段的中点,且 ,求的值;
解:
易知
由①②解得
更换基底
课堂探究
例2 在平行四边形中,探究以下问题:
(3) 分别是线段的中点,且 ,求的值;(4)在(3)的条件下,设为的内心,若 求的值.
解:
①
为的内心
②
由①②可知,又由可知
O
单位向量作基底
更换基底
课堂探究
问题4:什么样的向量常被选为基底?有什么特点?
O
三角形的
两条邻边
aa
已知
模长和夹角
的向量
平行四边形
的两条邻边
单位向量
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
敢选
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
任意两个不共线向量均可以作为基底,基底选择的合适与否将决定解答过程的繁杂或简洁。
敢选
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
任意两个不共线向量均可以作为基底,基底选择的合适与否将决定解答过程的繁杂或简洁。
敢选
优选
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
任意两个不共线向量均可以作为基底,基底选择的合适与否将决定解答过程的繁杂或简洁。
用基底表示相关向量后,除了做基本的向量运算之外,还有可能利用同一组基底分解的唯一性。
敢选
优选
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
任意两个不共线向量均可以作为基底,基底选择的合适与否将决定解答过程的繁杂或简洁。
用基底表示相关向量后,除了做基本的向量运算之外,还有可能利用同一组基底分解的唯一性。
敢选
巧用
优选
拓展应用:
平面向量的基底策略
与平面几何
/ 03
拓展应用(平面向量的基底策略与平面几何)
例3 在中, ,分别是线段的中点,若求的面积.
解:
方
法
一
基
底
法
坐标法可看作以为基底!
拓展应用(平面向量的基底策略与平面几何)
例3 在中,,分别是线段的中点,若求的面积.
解: 以中点为原点,如图所示建立坐标系
设点坐标为点A坐标为,则点B坐标为
为中点
,又解得
方
法
二
坐
标
法
思考讨论:
如何选择基底?
如何将所求向量用基底表示?
坐标法和基底法有怎样的关系?
拓展应用
例4 在中, 已知点分别是边的中点,点在边上,若则线段的长为___.
《平面向量的综合应用一》
热身训练
设分别是的三边线段上的点,且,则与( )
解:
反向平行 同向平行 互相垂直 既不平行也不垂直
无序 → 有序
基底
转化
平面向量综合应用中的基底策略
温故知新:
平面向量的基本定理
/ 01
温故知新
平面向量基本定理
如果、 是同一平面内的两个________向量,那么对于这一平面内的任意向量___________ 一对实数、,使得,其中、 称为一组_________.
填一填:
不共线
有且仅有
基底
温故知新
例1 在中,是线段的三等分点,则的值为.
问题1:利用基底法解决平面向量问题的基本步骤是什么?
基底法一般步骤:
①在平面图形中选取两个不共线向量;
②把问题中涉及的向量用进行线性表示;
③利用向量的运算法则和性质求解.
解:
未知 → 已知
基底
转化
课堂探究:
平面向量综合应用中的
基底策略
/ 02
课堂探究
例2 在平行四边形中,探究以下问题:
(1)为的中点,与交于点,且则.
问题2:未知模长或角度的向量可以作为基底吗?
解:
课堂探究
例2 在平行四边形中,探究以下问题:
(2) 已知是平行四边形所在平面上的一点,且满足 ,求的值.
问题3:本题的解题策略除了应用基底法之外,还运用了什么原理?
解:易知 ①
且
=
即 ②
由①②式可得解得,
平面向量基本定理: 同一组基底分解的唯一性
课堂探究
例2 在平行四边形中,探究以下问题:
(3) 分别是线段的中点,且 ,求的值;
解:
易知
由①②解得
更换基底
课堂探究
例2 在平行四边形中,探究以下问题:
(3) 分别是线段的中点,且 ,求的值;(4)在(3)的条件下,设为的内心,若 求的值.
解:
①
为的内心
②
由①②可知,又由可知
O
单位向量作基底
更换基底
课堂探究
问题4:什么样的向量常被选为基底?有什么特点?
O
三角形的
两条邻边
aa
已知
模长和夹角
的向量
平行四边形
的两条邻边
单位向量
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
敢选
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
任意两个不共线向量均可以作为基底,基底选择的合适与否将决定解答过程的繁杂或简洁。
敢选
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
任意两个不共线向量均可以作为基底,基底选择的合适与否将决定解答过程的繁杂或简洁。
敢选
优选
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
任意两个不共线向量均可以作为基底,基底选择的合适与否将决定解答过程的繁杂或简洁。
用基底表示相关向量后,除了做基本的向量运算之外,还有可能利用同一组基底分解的唯一性。
敢选
优选
课堂探究
对基底策略的感悟:
常见基底为已知模长或夹角的一组向量,但未知模长与夹角的向量也可以选择作基底。
任意两个不共线向量均可以作为基底,基底选择的合适与否将决定解答过程的繁杂或简洁。
用基底表示相关向量后,除了做基本的向量运算之外,还有可能利用同一组基底分解的唯一性。
敢选
巧用
优选
拓展应用:
平面向量的基底策略
与平面几何
/ 03
拓展应用(平面向量的基底策略与平面几何)
例3 在中, ,分别是线段的中点,若求的面积.
解:
方
法
一
基
底
法
坐标法可看作以为基底!
拓展应用(平面向量的基底策略与平面几何)
例3 在中,,分别是线段的中点,若求的面积.
解: 以中点为原点,如图所示建立坐标系
设点坐标为点A坐标为,则点B坐标为
为中点
,又解得
方
法
二
坐
标
法
思考讨论:
如何选择基底?
如何将所求向量用基底表示?
坐标法和基底法有怎样的关系?
拓展应用
例4 在中, 已知点分别是边的中点,点在边上,若则线段的长为___.
同课章节目录
