基于数学抽象素养提升的空间角教学(共31张PPT)
文档属性
| 名称 | 基于数学抽象素养提升的空间角教学(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 16:58:10 | ||
图片预览








文档简介
(共31张PPT)
基于数学抽象素养
提升的空间角教学
一、课程标准分析
《课程标准(2017版)》中明确提岀数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象的素养。
主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物具体背景中抽象出一般规律和结构,并用数学语言予以表征。
一、课程标准分析
数学抽象是数学的基本思想,是形成理性思维的重要基础,反映了数学的本质特征,贯穿在数学产生、发展、应用的过程中。数学抽象使得数学成为高度概括、表达准确、结论一般、有序多级的系统.
数学抽象主要表现为:
获得数学概念和规则,提出数学命题和模型,
形成数学方法与思想,认识数学结构与体系。
一、课程标准分析
通过高中数学课程的学习,学生能在情境中抽象出数学概念、命题、方法和体系,积累从具体到抽象的活动经验;养成在日常生活和实践中一般性思考问题的习惯,把握事物的本质,以简御繁;运用数学抽象的思维方式思考并解决问题.
数学抽象素养的一般表现
概念析取:从情境中获得概念、规则、命题、运算、关系
语言表达:用数学语言对概念、规则、推理、论证进行表达
方法普适:利用或创造数学方法解决问题并对其进行解释
二、空间角教学要素分析
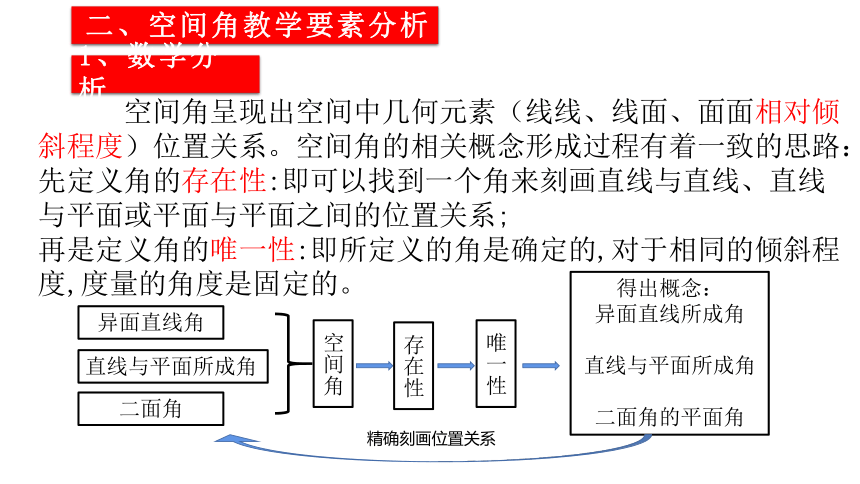
空间角呈现出空间中几何元素(线线、线面、面面相对倾斜程度)位置关系。空间角的相关概念形成过程有着一致的思路:
先定义角的存在性:即可以找到一个角来刻画直线与直线、直线与平面或平面与平面之间的位置关系;
再是定义角的唯一性:即所定义的角是确定的,对于相同的倾斜程度,度量的角度是固定的。
异面直线角
直线与平面所成角
二面角
空间角
存在性
唯一性
得出概念:
异面直线所成角
直线与平面所成角
二面角的平面角
精确刻画位置关系
1、数学分析
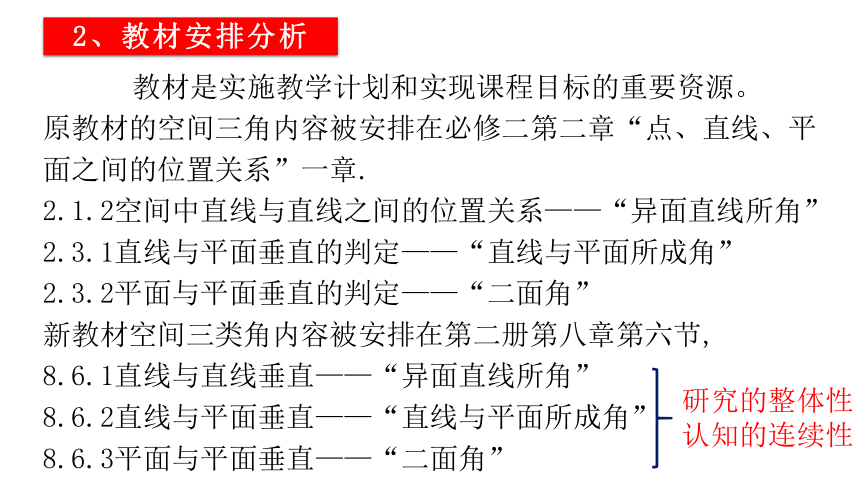
2、教材安排分析
教材是实施教学计划和实现课程目标的重要资源。
原教材的空间三角内容被安排在必修二第二章“点、直线、平面之间的位置关系”一章.
2.1.2空间中直线与直线之间的位置关系——“异面直线所角”
2.3.1直线与平面垂直的判定——“直线与平面所成角”
2.3.2平面与平面垂直的判定——“二面角”
新教材空间三类角内容被安排在第二册第八章第六节,
8.6.1直线与直线垂直——“异面直线所角”
8.6.2直线与平面垂直——“直线与平面所成角”
8.6.3平面与平面垂直——“二面角”
研究的整体性
认知的连续性
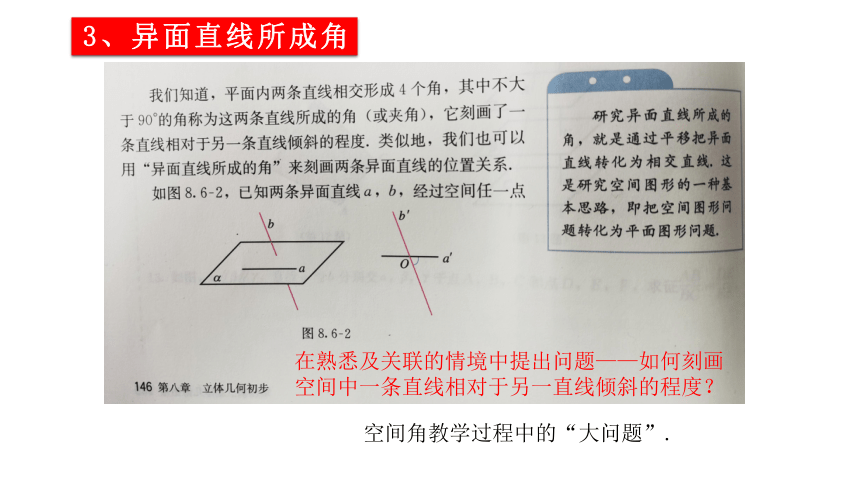
3、异面直线所成角
在熟悉及关联的情境中提出问题——如何刻画
空间中一条直线相对于另一直线倾斜的程度?
空间角教学过程中的“大问题”.
3、异面直线所成角
空间等角定理
保证了所度量的异面直线成角的唯一性!
从一般到特殊,定义两条异面直线的互相垂直.
3、异面直线所成角
指明了空间角度量的基本思想方法
转化
降维
空间问题
平面问题
体现了在空间中观察两条异面直线的相对倾斜程度,由两条异面直线唯一确定,与O点位置无关.
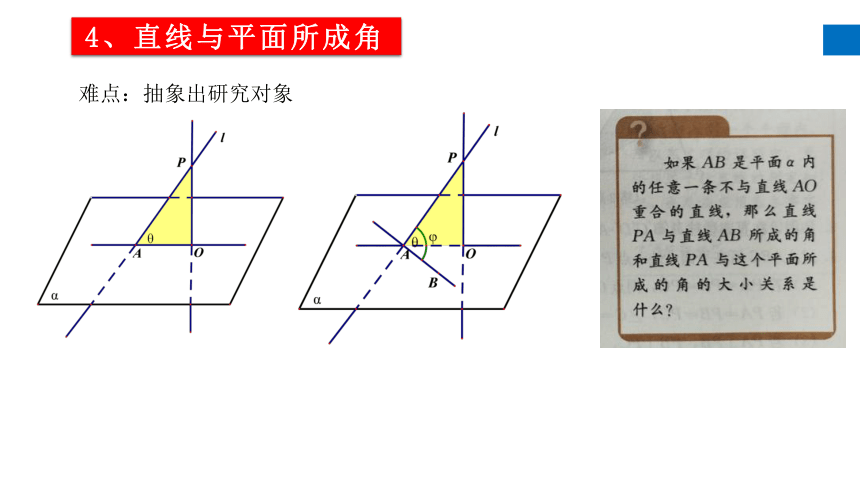
4、直线与平面所成角
直接给出定义的同时提出问题,重在引导理性思考,理解线面角定义的合理性
存在且唯一
线面角是斜线与该平面内所有直线所成角中的
最小角
转化
降维
空间问题
平面问题
难点:抽象出研究对象
4、直线与平面所成角
难点:抽象出研究对象
抽象几何模型
引导定性观察
构造垂直关系
寻求函数表达
发现斜边相等
得到比较关系
4、直线与平面所成角
确定函数表达
难点:寻找比较的策略
(1)如何理解直线AB可以表示平面内的任意一条直线?
(2)如何定量刻画直线AB与射影AO的相对位置关系?
4、直线与平面所成角
3、教材分析
(1)如何理解直线AB可以表示平面内的任意一条直线?
平面α内任意直线与斜线 的位置关系?
相交与点A
两直线异面
对于平面α内任意一直线m,总能找到过A的直线AB//直线m.
4、直线与平面所成角
异面直线
所成的角
(2)如何定量刻画直线AB与射影AO的相对位置关系?
直线AB与射影AO所成角为β,0°≤β≤90°
模型中的三个角 有怎样的定量关系?
再次选择函数表达
三余弦关系
定性
定量
4、直线与平面所成角
存在且唯一
猜想与证明
直觉与理性
直观感知
操作确认
度量计算
推理论证
获得基本研究套路
积累基本活动经验
提升数学抽象素养
4、直线与平面所成角
5、二面角的平面角
难点:如何度量二面角的大小。
5、二面角的平面角
根据异面直线所成角的研究经验
“平面化”思想
用“平面角”定量刻画两个半平面间的
相对倾斜程度.
已在线面角研究中获得成功
度量一个量:存在且唯一
根据直线与平面
所成角的研究经验
基本研究套路:
感知与猜想
操作与确认
推理与证明
直觉
理性
猜想
证明
定性
定量
5、二面角的平面角
教师教学用书,数学必修第二册
线面角
线线角
二面角
平面化
5、二面角的平面角
线面角
线线角
二面角
平面化
在半平面β内任取直线AB
构造直线AB与平面α所成的角θ
5、二面角的平面角
由线面角的研究经验:
平面β内绕着A点旋转的直线可以代替平面内的任意直线.
动态演示使学生直观感知随B点的运动,也可以让学生操作用折纸减去一角的方法直观呈现,感知直线AB与平面α所成角的唯一性,从而直观猜想B点的位置.
5、二面角的平面角
抽象几何模型
直观定性观察
构造垂直关系
寻求函数表达
距离AC不变
得到比较关系
由于 体现了 的唯一性,同时得到二面角的平面角是一个半平面内的任意一条直线与另一个半平面所成的线面角中的最大角.
确认位置
5、二面角的平面角
结合线面角的
最小角证明经验:
定性比较
定量刻画
选择合适的函数
由二面角棱的确定性
得到三正弦关系:
其中 是半平面内的任意一直线与另一半平面所成的角, 是此直线与棱所成的角, 是锐二面角的平面角.
5、二面角的平面角
二面角
半平面α
半平面β
棱
定量
刻画
平面角
(存在)
直观
感知
垂直与棱的直线与
另一个半平面所成角
推理
证明
最大角
(唯一)
学生能在知识发生发展的过程中,经历将“空间角”转化为“平面角”的过程,经历“角的存在性”“角的唯一性”的发现过程与“角的唯一性”的证明过程,从而提升数学抽象素养.
共同确认二面角的平面角的作法,并体会与点O的位置无关
线面角
转化
逐级
5、二面角的平面角
迁移转化
类比同化
5、二面角的平面角
6、关注重点模型
鳖臑(biē nào):在我国三角锥体的古称.
现代白话文:四个面均为直角三角形的三棱锥.
长方体
阳 马
鳖臑
6、关注重点模型
7、关注课后习题
为空间向量在立体几何中的应用铺垫.
直线m,n确定平面α,则l1,l2,可以与平面的法向量联系.
直线a//b,对于确定的平面α,则a,b与平面α所成的角相等.
对于同一条直线,与两个平行的平面所成的角相等.
有助于在向量法研究空间角的过程中对直线方向向量、平面法向量的理解.
13.求证:两条平行直线与同一个平面所成的角相等。
12.如图,m,n是两条相交直线,l1,l2是与m,n都垂直的两条直线,且直线l与l1,l2都相交,求证∠1=∠2。
谢 谢!
基于数学抽象素养
提升的空间角教学
一、课程标准分析
《课程标准(2017版)》中明确提岀数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象的素养。
主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物具体背景中抽象出一般规律和结构,并用数学语言予以表征。
一、课程标准分析
数学抽象是数学的基本思想,是形成理性思维的重要基础,反映了数学的本质特征,贯穿在数学产生、发展、应用的过程中。数学抽象使得数学成为高度概括、表达准确、结论一般、有序多级的系统.
数学抽象主要表现为:
获得数学概念和规则,提出数学命题和模型,
形成数学方法与思想,认识数学结构与体系。
一、课程标准分析
通过高中数学课程的学习,学生能在情境中抽象出数学概念、命题、方法和体系,积累从具体到抽象的活动经验;养成在日常生活和实践中一般性思考问题的习惯,把握事物的本质,以简御繁;运用数学抽象的思维方式思考并解决问题.
数学抽象素养的一般表现
概念析取:从情境中获得概念、规则、命题、运算、关系
语言表达:用数学语言对概念、规则、推理、论证进行表达
方法普适:利用或创造数学方法解决问题并对其进行解释
二、空间角教学要素分析
空间角呈现出空间中几何元素(线线、线面、面面相对倾斜程度)位置关系。空间角的相关概念形成过程有着一致的思路:
先定义角的存在性:即可以找到一个角来刻画直线与直线、直线与平面或平面与平面之间的位置关系;
再是定义角的唯一性:即所定义的角是确定的,对于相同的倾斜程度,度量的角度是固定的。
异面直线角
直线与平面所成角
二面角
空间角
存在性
唯一性
得出概念:
异面直线所成角
直线与平面所成角
二面角的平面角
精确刻画位置关系
1、数学分析
2、教材安排分析
教材是实施教学计划和实现课程目标的重要资源。
原教材的空间三角内容被安排在必修二第二章“点、直线、平面之间的位置关系”一章.
2.1.2空间中直线与直线之间的位置关系——“异面直线所角”
2.3.1直线与平面垂直的判定——“直线与平面所成角”
2.3.2平面与平面垂直的判定——“二面角”
新教材空间三类角内容被安排在第二册第八章第六节,
8.6.1直线与直线垂直——“异面直线所角”
8.6.2直线与平面垂直——“直线与平面所成角”
8.6.3平面与平面垂直——“二面角”
研究的整体性
认知的连续性
3、异面直线所成角
在熟悉及关联的情境中提出问题——如何刻画
空间中一条直线相对于另一直线倾斜的程度?
空间角教学过程中的“大问题”.
3、异面直线所成角
空间等角定理
保证了所度量的异面直线成角的唯一性!
从一般到特殊,定义两条异面直线的互相垂直.
3、异面直线所成角
指明了空间角度量的基本思想方法
转化
降维
空间问题
平面问题
体现了在空间中观察两条异面直线的相对倾斜程度,由两条异面直线唯一确定,与O点位置无关.
4、直线与平面所成角
直接给出定义的同时提出问题,重在引导理性思考,理解线面角定义的合理性
存在且唯一
线面角是斜线与该平面内所有直线所成角中的
最小角
转化
降维
空间问题
平面问题
难点:抽象出研究对象
4、直线与平面所成角
难点:抽象出研究对象
抽象几何模型
引导定性观察
构造垂直关系
寻求函数表达
发现斜边相等
得到比较关系
4、直线与平面所成角
确定函数表达
难点:寻找比较的策略
(1)如何理解直线AB可以表示平面内的任意一条直线?
(2)如何定量刻画直线AB与射影AO的相对位置关系?
4、直线与平面所成角
3、教材分析
(1)如何理解直线AB可以表示平面内的任意一条直线?
平面α内任意直线与斜线 的位置关系?
相交与点A
两直线异面
对于平面α内任意一直线m,总能找到过A的直线AB//直线m.
4、直线与平面所成角
异面直线
所成的角
(2)如何定量刻画直线AB与射影AO的相对位置关系?
直线AB与射影AO所成角为β,0°≤β≤90°
模型中的三个角 有怎样的定量关系?
再次选择函数表达
三余弦关系
定性
定量
4、直线与平面所成角
存在且唯一
猜想与证明
直觉与理性
直观感知
操作确认
度量计算
推理论证
获得基本研究套路
积累基本活动经验
提升数学抽象素养
4、直线与平面所成角
5、二面角的平面角
难点:如何度量二面角的大小。
5、二面角的平面角
根据异面直线所成角的研究经验
“平面化”思想
用“平面角”定量刻画两个半平面间的
相对倾斜程度.
已在线面角研究中获得成功
度量一个量:存在且唯一
根据直线与平面
所成角的研究经验
基本研究套路:
感知与猜想
操作与确认
推理与证明
直觉
理性
猜想
证明
定性
定量
5、二面角的平面角
教师教学用书,数学必修第二册
线面角
线线角
二面角
平面化
5、二面角的平面角
线面角
线线角
二面角
平面化
在半平面β内任取直线AB
构造直线AB与平面α所成的角θ
5、二面角的平面角
由线面角的研究经验:
平面β内绕着A点旋转的直线可以代替平面内的任意直线.
动态演示使学生直观感知随B点的运动,也可以让学生操作用折纸减去一角的方法直观呈现,感知直线AB与平面α所成角的唯一性,从而直观猜想B点的位置.
5、二面角的平面角
抽象几何模型
直观定性观察
构造垂直关系
寻求函数表达
距离AC不变
得到比较关系
由于 体现了 的唯一性,同时得到二面角的平面角是一个半平面内的任意一条直线与另一个半平面所成的线面角中的最大角.
确认位置
5、二面角的平面角
结合线面角的
最小角证明经验:
定性比较
定量刻画
选择合适的函数
由二面角棱的确定性
得到三正弦关系:
其中 是半平面内的任意一直线与另一半平面所成的角, 是此直线与棱所成的角, 是锐二面角的平面角.
5、二面角的平面角
二面角
半平面α
半平面β
棱
定量
刻画
平面角
(存在)
直观
感知
垂直与棱的直线与
另一个半平面所成角
推理
证明
最大角
(唯一)
学生能在知识发生发展的过程中,经历将“空间角”转化为“平面角”的过程,经历“角的存在性”“角的唯一性”的发现过程与“角的唯一性”的证明过程,从而提升数学抽象素养.
共同确认二面角的平面角的作法,并体会与点O的位置无关
线面角
转化
逐级
5、二面角的平面角
迁移转化
类比同化
5、二面角的平面角
6、关注重点模型
鳖臑(biē nào):在我国三角锥体的古称.
现代白话文:四个面均为直角三角形的三棱锥.
长方体
阳 马
鳖臑
6、关注重点模型
7、关注课后习题
为空间向量在立体几何中的应用铺垫.
直线m,n确定平面α,则l1,l2,可以与平面的法向量联系.
直线a//b,对于确定的平面α,则a,b与平面α所成的角相等.
对于同一条直线,与两个平行的平面所成的角相等.
有助于在向量法研究空间角的过程中对直线方向向量、平面法向量的理解.
13.求证:两条平行直线与同一个平面所成的角相等。
12.如图,m,n是两条相交直线,l1,l2是与m,n都垂直的两条直线,且直线l与l1,l2都相交,求证∠1=∠2。
谢 谢!
同课章节目录
