高考备考专题复习:立体几何中的切割与补形 课件(共23张PPT)
文档属性
| 名称 | 高考备考专题复习:立体几何中的切割与补形 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 20:23:59 | ||
图片预览


文档简介
(共23张PPT)
高考备考专题复习
立体几何中的切割与补形
“切割”与“补形”在立体几何中有着广泛的应用,常常起到化“难”为“易”、化“繁”为“简”的作用,甚至可以将不可能变为可能!
地位与作用
巧用割补法快速解决立体几何问题
目的与目标
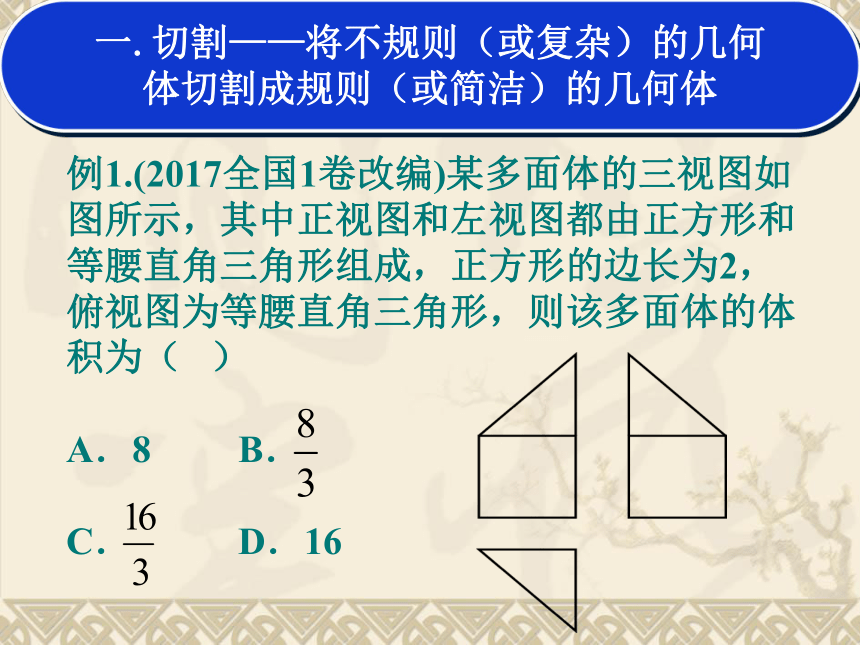
例1.(2017全国1卷改编)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,则该多面体的体积为( )
A.8 B.
C. D.16
一.切割——将不规则(或复杂)的几何
体切割成规则(或简洁)的几何体
分析:由三视图可知该多面体如图所示,没有公式能直接求出它的体积。但我们可将它切割为一个直三棱柱和一个三棱锥。
易知它们的底面均是等腰直角三角形,高均是2。故该多面体的体积为
快速解决!
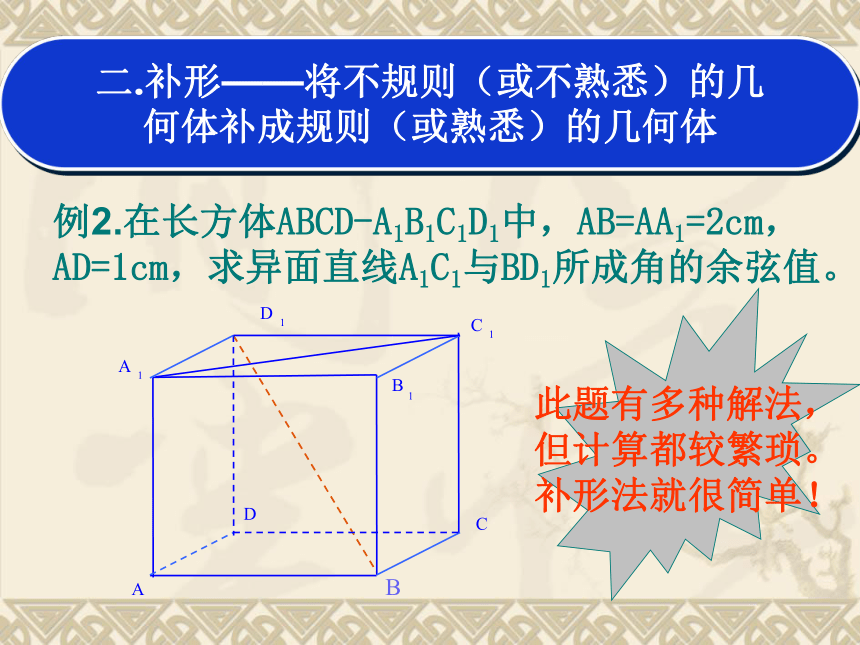
例2.在长方体ABCD-A1B1C1D1中,AB=AA1=2cm,AD=1cm,求异面直线A1C1与BD1所成角的余弦值。
D
B
1
A
1
D
1
C
1
A
C
B
此题有多种解法,
但计算都较繁琐。
补形法就很简单!
二.补形——将不规则(或不熟悉)的几
何体补成规则(或熟悉)的几何体
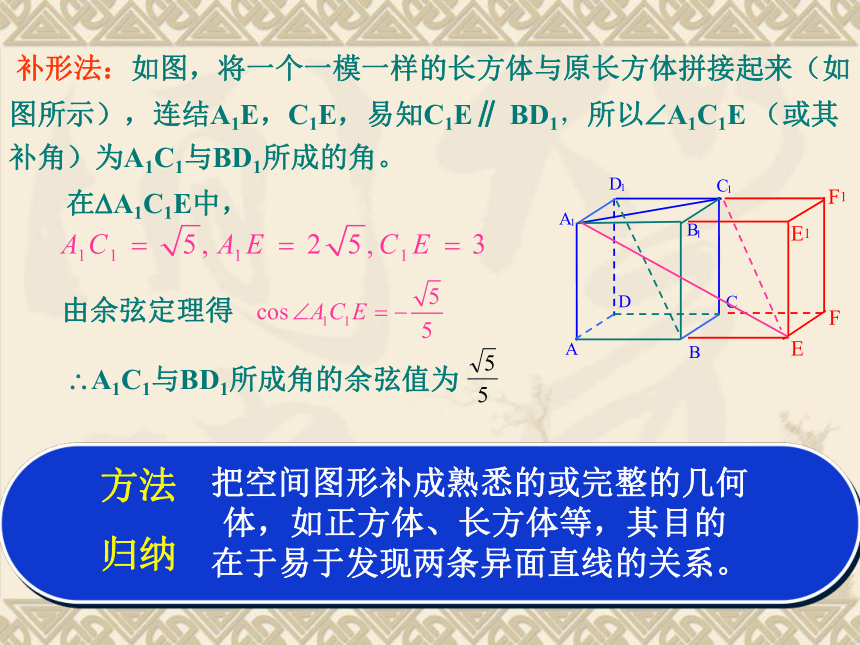
在 A1C1E中,
由余弦定理得
A1C1与BD1所成角的余弦值为
补形法:如图,将一个一模一样的长方体与原长方体拼接起来(如图所示),连结A1E,C1E,易知C1E∥ BD1,所以 A1C1E (或其补角)为A1C1与BD1所成的角。
F1
E
F
E1
B
D
B
1
A
1
D
1
C
1
A
C
把空间图形补成熟悉的或完整的几何
体,如正方体、长方体等,其目的
在于易于发现两条异面直线的关系。
方法
归纳
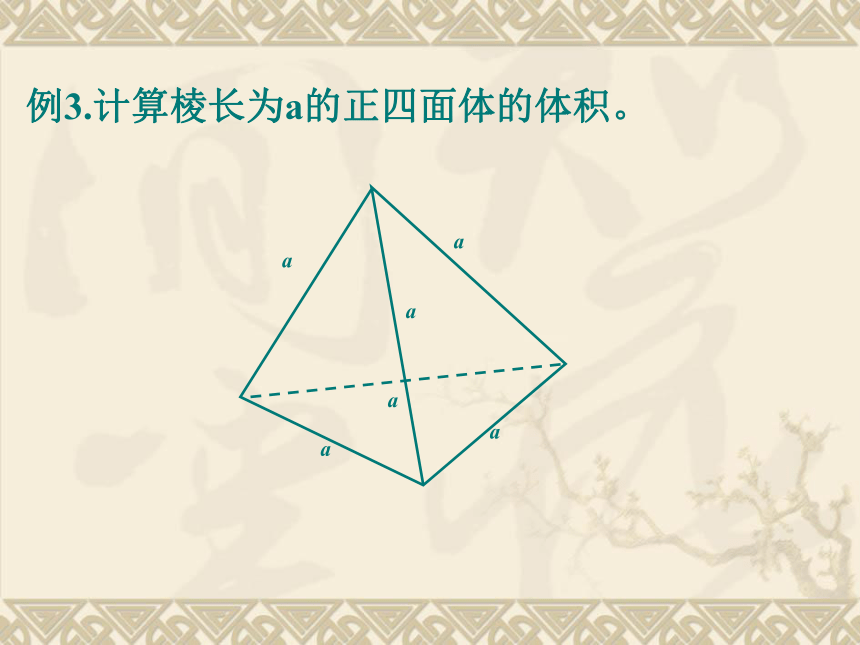
例3.计算棱长为a的正四面体的体积。
a
a
a
a
a
a
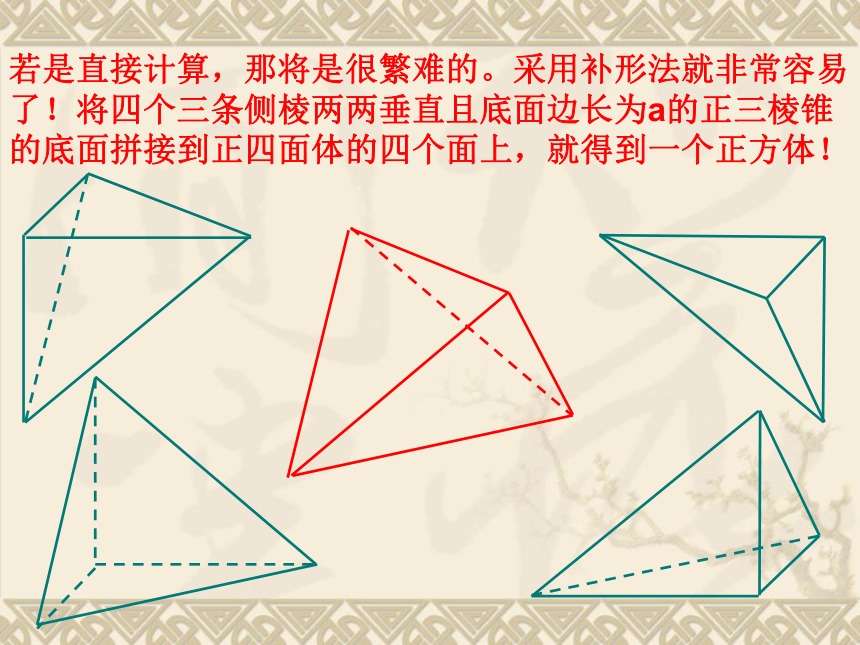
若是直接计算,那将是很繁难的。采用补形法就非常容易了!将四个三条侧棱两两垂直且底面边长为a的正三棱锥的底面拼接到正四面体的四个面上,就得到一个正方体!
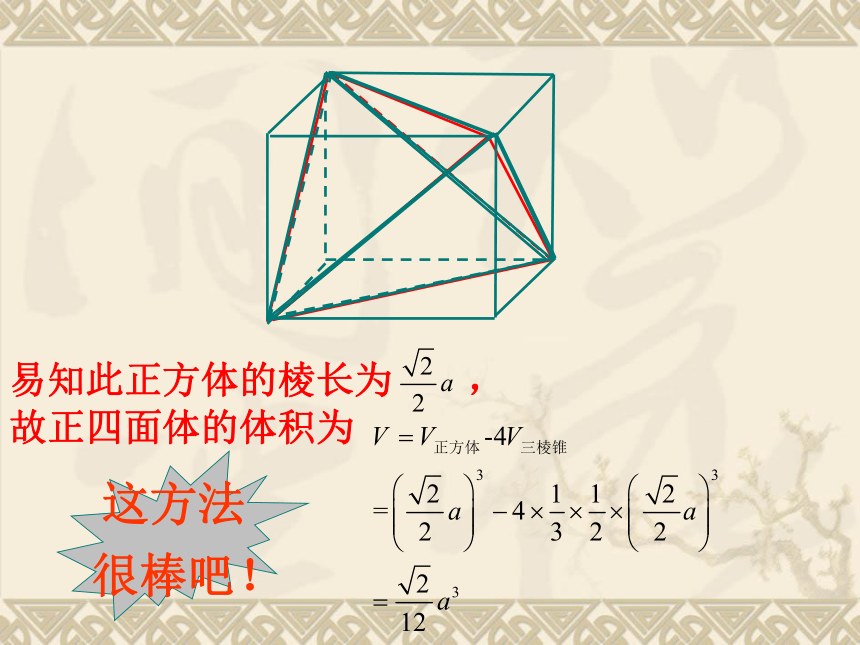
易知此正方体的棱长为 ,
故正四面体的体积为
这方法
很棒吧!
1.如图,一个三棱锥的三视图均为直角三角形,若该三棱锥的顶点都在同一个球面上,则该球的表面积为( )。
(A)4π (B)16π
(C)24π (D)25π
练习一
画出三棱锥的直观图,不难发现,这是一个有三条棱
两两垂直的三棱锥,补形为长方体,问题就非常
容易解决了。
O
A
B
C
2
2
4
显然有(2R)2=22+22+42,故R2=6,S球=24π,因此选C。
A
B
C
D
O
解析:此题若直接求解,计算也
是很繁琐的。
2 . 一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为( )
A. B. C. D.
A
将此正四面体补形成正方体,
则正方体棱长为 1,
外接球半径为 ,
表面积为 。
a
a
a
a
a
a
三. 正四面体的内切球半径问题——切割法
构造三角形利用相似比和勾股定理。此法既难又繁!切割法非常简洁!
基本方法
快速解法
分别以正四面体的四个面为底、
以内切球球心为顶点,将正四
面体切割为四个三棱锥。
(1)这四个三棱锥的高与内切球的半径有何关系?
(2)这四个三棱锥的体积与原正四面体的体积有什么关系呢?
想一想
(1)这四个三棱锥的高都等于内切球的半径。
(2)这四个三棱锥的体积之和等于原正四面体的体积。
结论
所以,有
解:如图,设内切球半径为r,PH是正三棱锥的高,即PH=1,E是BC的中点,则H在AE上, ABC的边长 ,
∴ ,∴ ,
∴ ,
由切割法得
例4.正三棱锥的高为1,底面边长为 ,正三棱锥内有一个球与其四个面相切.求球的表面积与体积.
∴
∴
∴
P
A
B
C
O
E
H
例5.在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,那么这个球面的面积是_______.
P
A
B
C
这也太
难了吧!
这其实就是正三棱锥外接球问题。
四. 四面体的外接球半径问题——补形法
A
C
B
P
O
难则思变:将三棱锥P-ABC补成正方体,
正方体的棱长为a,且正方体的对角线就是球的直径!
因此 ,所以 。
秒杀!
A
C
B
P
O
1 . 若三棱锥的三条侧棱两两垂直,且侧棱长分别为 、
、 ,则其外接球的体积等于 .
解析:此题直接求解,
计算将很繁琐。
这个三棱锥可补形成长方体,这样求解就简便得多了。
易得长方体对角线长为 ,所以球的半径为 ,因此球的体
积为 。
练习二
2.一个几何体的三视图如图所示,三视图都是腰长为2 的等腰直角三角形, 则该几何体的外接球半径与内切球半径之比为 .
解:依题意知几何体是正三棱锥,且三条侧棱两两垂直,
设内切球的半径为r,由切割法可得:
解得 ,
该几何体的外接球半径与内切球半径之比为
答案: .
故可将其补形为正方体,如图所示,正方体的棱长
为 2 ,故外接球的半径为 ,
(1)几何体的“切割”与“补形”的基本思想是将不规则的、复杂的或不熟悉的几何体进行“割”或“补”,使之成为有规则的、简洁的或熟悉的几何体。
(2)“割”或“补”成长方体(正方体)是最常见的割补方法,故要熟记长方体(正方体)的基本性质、公式及有关结论。
课堂小结
高考备考专题复习
立体几何中的切割与补形
“切割”与“补形”在立体几何中有着广泛的应用,常常起到化“难”为“易”、化“繁”为“简”的作用,甚至可以将不可能变为可能!
地位与作用
巧用割补法快速解决立体几何问题
目的与目标
例1.(2017全国1卷改编)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,则该多面体的体积为( )
A.8 B.
C. D.16
一.切割——将不规则(或复杂)的几何
体切割成规则(或简洁)的几何体
分析:由三视图可知该多面体如图所示,没有公式能直接求出它的体积。但我们可将它切割为一个直三棱柱和一个三棱锥。
易知它们的底面均是等腰直角三角形,高均是2。故该多面体的体积为
快速解决!
例2.在长方体ABCD-A1B1C1D1中,AB=AA1=2cm,AD=1cm,求异面直线A1C1与BD1所成角的余弦值。
D
B
1
A
1
D
1
C
1
A
C
B
此题有多种解法,
但计算都较繁琐。
补形法就很简单!
二.补形——将不规则(或不熟悉)的几
何体补成规则(或熟悉)的几何体
在 A1C1E中,
由余弦定理得
A1C1与BD1所成角的余弦值为
补形法:如图,将一个一模一样的长方体与原长方体拼接起来(如图所示),连结A1E,C1E,易知C1E∥ BD1,所以 A1C1E (或其补角)为A1C1与BD1所成的角。
F1
E
F
E1
B
D
B
1
A
1
D
1
C
1
A
C
把空间图形补成熟悉的或完整的几何
体,如正方体、长方体等,其目的
在于易于发现两条异面直线的关系。
方法
归纳
例3.计算棱长为a的正四面体的体积。
a
a
a
a
a
a
若是直接计算,那将是很繁难的。采用补形法就非常容易了!将四个三条侧棱两两垂直且底面边长为a的正三棱锥的底面拼接到正四面体的四个面上,就得到一个正方体!
易知此正方体的棱长为 ,
故正四面体的体积为
这方法
很棒吧!
1.如图,一个三棱锥的三视图均为直角三角形,若该三棱锥的顶点都在同一个球面上,则该球的表面积为( )。
(A)4π (B)16π
(C)24π (D)25π
练习一
画出三棱锥的直观图,不难发现,这是一个有三条棱
两两垂直的三棱锥,补形为长方体,问题就非常
容易解决了。
O
A
B
C
2
2
4
显然有(2R)2=22+22+42,故R2=6,S球=24π,因此选C。
A
B
C
D
O
解析:此题若直接求解,计算也
是很繁琐的。
2 . 一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为( )
A. B. C. D.
A
将此正四面体补形成正方体,
则正方体棱长为 1,
外接球半径为 ,
表面积为 。
a
a
a
a
a
a
三. 正四面体的内切球半径问题——切割法
构造三角形利用相似比和勾股定理。此法既难又繁!切割法非常简洁!
基本方法
快速解法
分别以正四面体的四个面为底、
以内切球球心为顶点,将正四
面体切割为四个三棱锥。
(1)这四个三棱锥的高与内切球的半径有何关系?
(2)这四个三棱锥的体积与原正四面体的体积有什么关系呢?
想一想
(1)这四个三棱锥的高都等于内切球的半径。
(2)这四个三棱锥的体积之和等于原正四面体的体积。
结论
所以,有
解:如图,设内切球半径为r,PH是正三棱锥的高,即PH=1,E是BC的中点,则H在AE上, ABC的边长 ,
∴ ,∴ ,
∴ ,
由切割法得
例4.正三棱锥的高为1,底面边长为 ,正三棱锥内有一个球与其四个面相切.求球的表面积与体积.
∴
∴
∴
P
A
B
C
O
E
H
例5.在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,那么这个球面的面积是_______.
P
A
B
C
这也太
难了吧!
这其实就是正三棱锥外接球问题。
四. 四面体的外接球半径问题——补形法
A
C
B
P
O
难则思变:将三棱锥P-ABC补成正方体,
正方体的棱长为a,且正方体的对角线就是球的直径!
因此 ,所以 。
秒杀!
A
C
B
P
O
1 . 若三棱锥的三条侧棱两两垂直,且侧棱长分别为 、
、 ,则其外接球的体积等于 .
解析:此题直接求解,
计算将很繁琐。
这个三棱锥可补形成长方体,这样求解就简便得多了。
易得长方体对角线长为 ,所以球的半径为 ,因此球的体
积为 。
练习二
2.一个几何体的三视图如图所示,三视图都是腰长为2 的等腰直角三角形, 则该几何体的外接球半径与内切球半径之比为 .
解:依题意知几何体是正三棱锥,且三条侧棱两两垂直,
设内切球的半径为r,由切割法可得:
解得 ,
该几何体的外接球半径与内切球半径之比为
答案: .
故可将其补形为正方体,如图所示,正方体的棱长
为 2 ,故外接球的半径为 ,
(1)几何体的“切割”与“补形”的基本思想是将不规则的、复杂的或不熟悉的几何体进行“割”或“补”,使之成为有规则的、简洁的或熟悉的几何体。
(2)“割”或“补”成长方体(正方体)是最常见的割补方法,故要熟记长方体(正方体)的基本性质、公式及有关结论。
课堂小结
同课章节目录
