广东省汕头市金平区东厦中学2011-2012学年高一上学期期末考试数学试题
文档属性
| 名称 | 广东省汕头市金平区东厦中学2011-2012学年高一上学期期末考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 158.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-08 15:32:46 | ||
图片预览


文档简介
东厦中学2011—2012学年度第一学期期末考试
高一级数学科试卷
命题: , 教研组长:
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择)题两部分,满分150分.考试用时120分钟.
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.
1. 设全集U={-1,0,1,2,3},A={-1,0},B={0,1,2},则(CUA)∩B =( )
(A) {0} (B) {-2,-1} (C) {1,2 } (D) {0,1,2}
2. 己知向量a=(2,1), b=(-3,4),则a-b=( )
(A)(5,) (B)(1,) (C)(5,3) (D)(,3)
3.函数最小正周期是
(A) (B) (C) (D)
4.若是两个单位向量,则( )
(A) (B) (C) (D)
5.函数在区间上( )21世纪教育网
(A)没有零点 (B)只有一个零点 (C)有两个零点 (D)以上选项都错误
6.设扇形的周长为6,面积为2,则扇形的圆心角是(弧度)( )
(A) 1 (B) 4 (C) (D) 1或4
7.为了得到函数的图象,只需把函数的图象上所有的点( )
(A)向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍
(B)向右平移个单位长度,再把所得各点的横坐标缩短到原来的倍
(C)向左平移个单位长度,再把所得各点的横坐标伸长到原来的3倍
(D)向右平移个单位长度,再把所得各点的横坐标伸长到原来的3倍
8.函数 对任意自然数,满足( )
(A)11 (B)12 (C)13 (D)14
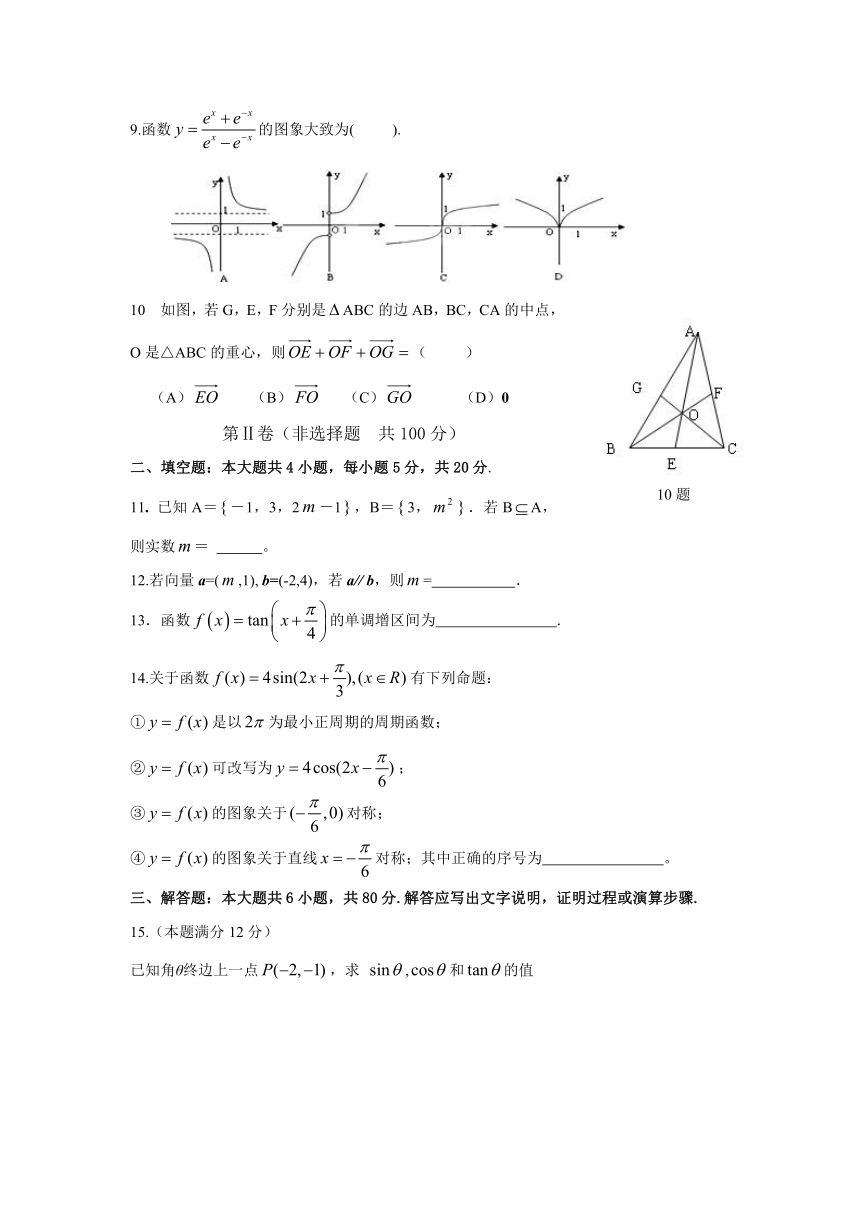
9.函数的图象大致为( ).
10 如图,若G,E,F分别是ABC的边AB,BC,CA的中点,O是△ABC的重心,则( )
(A) (B) (C) (D)0
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共4小题,每小题5分,共20分.
11. 已知A=-1,3,2-1,B=3,.若BA,则实数= 。
12.若向量a=(,1), b=(-2,4),若a// b,则= .
13.函数的单调增区间为 .
14.关于函数有下列命题:
①是以为最小正周期的周期函数;
②可改写为;
③的图象关于对称;
④的图象关于直线对称;其中正确的序号为 。
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分12分)
已知角θ终边上一点,求 ,和的值
16.(本题满分12分)
自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
(1)写出的解析式;
(2)若某用户该月用水21吨,则该用户需要缴水费多少钱?
17.(本题满分14分)
已知是关于的方程“”的两根
1)求实数的值; 2)求的值.
18. (本题满分14分)
已知函数,R.
(1)求它的振幅、周期、初相;
(2)用五点法作出一个周期的简图;
(3)该函数的图象可由(R)的图象经过怎样的平移和伸缩变换得到?
19. (本题满分14分)
已知(其中)的图象与轴的交点中,相邻两个交点之间的距离为.若为图象上一个最低点.
(1)求的解析式;
(2)求函数图象的对称轴方程和对称中心坐标.
(3)已知求函数的值域.
20. (本题满分14分)
设函数,函数.且当时,恒成立,
1)当时,求不等式的解集;
2)求的最大值;
3)当m取最大值时,判断的奇偶性并给予证明.
东厦中学2011—2012学年度第一学期期末考试
高一级数学科试卷参考答案
一、选择题
CACDB DCAA D
二、填空题
11.1 12. 13. 14.②③
三、解答题
15. 解:∵角θ终边上一点,
由三角函数的定义可得:
∴
∴,
16. 解:(1)设直线OA的解析式为y=ax(0x15),依题意得,
把点A(15,27)代入得,15a=27 解得 a=1.8
则直线OA的解析式为y=1.8x(0x15)
设直线AB的解析式为y=a’x+b (x>15)
把点A(15,27)和点(20,39.5)代入得 解得
则直线AB的解析式为y=2.5x-10.5(x>15)
即 y=f(x)=
(2)当x=21时,y=2.521-10.5=42
若该用户用水21吨,则该用户需交水费42元。
17. 解:(1)是关于的方程的两根,
(2)原式=
18. 1、解:(1)函数的振幅为,周期为,初相为.
(2)列表:
0
0
0
画简图:
(3)解法1:
函数的图象 函数的图象,
函数的图象,
函数的图.
解法2:函数的图象
函数的图象 函数的图象
函数的图象.
19、(1)由题意知,所以,即,故,
又且,所以,,所以,
所以函数解析式是;
(2)令,得,
即函数图象的对称轴方程为;21世纪教育网
令,得,
(3),,,
所以函数的值域为
20.解:(1)当时,由解得,
故不等式的解集为.
配方得,,
∵时,恒成立,
即恒成立,
∴
令,对称轴为,
则,
∴,故的最大值为3.
由(2)知,,
由解得,故.
又,
∴
故是奇函数.
高一级数学科试卷
命题: , 教研组长:
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择)题两部分,满分150分.考试用时120分钟.
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.
1. 设全集U={-1,0,1,2,3},A={-1,0},B={0,1,2},则(CUA)∩B =( )
(A) {0} (B) {-2,-1} (C) {1,2 } (D) {0,1,2}
2. 己知向量a=(2,1), b=(-3,4),则a-b=( )
(A)(5,) (B)(1,) (C)(5,3) (D)(,3)
3.函数最小正周期是
(A) (B) (C) (D)
4.若是两个单位向量,则( )
(A) (B) (C) (D)
5.函数在区间上( )21世纪教育网
(A)没有零点 (B)只有一个零点 (C)有两个零点 (D)以上选项都错误
6.设扇形的周长为6,面积为2,则扇形的圆心角是(弧度)( )
(A) 1 (B) 4 (C) (D) 1或4
7.为了得到函数的图象,只需把函数的图象上所有的点( )
(A)向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍
(B)向右平移个单位长度,再把所得各点的横坐标缩短到原来的倍
(C)向左平移个单位长度,再把所得各点的横坐标伸长到原来的3倍
(D)向右平移个单位长度,再把所得各点的横坐标伸长到原来的3倍
8.函数 对任意自然数,满足( )
(A)11 (B)12 (C)13 (D)14
9.函数的图象大致为( ).
10 如图,若G,E,F分别是ABC的边AB,BC,CA的中点,O是△ABC的重心,则( )
(A) (B) (C) (D)0
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共4小题,每小题5分,共20分.
11. 已知A=-1,3,2-1,B=3,.若BA,则实数= 。
12.若向量a=(,1), b=(-2,4),若a// b,则= .
13.函数的单调增区间为 .
14.关于函数有下列命题:
①是以为最小正周期的周期函数;
②可改写为;
③的图象关于对称;
④的图象关于直线对称;其中正确的序号为 。
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分12分)
已知角θ终边上一点,求 ,和的值
16.(本题满分12分)
自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
(1)写出的解析式;
(2)若某用户该月用水21吨,则该用户需要缴水费多少钱?
17.(本题满分14分)
已知是关于的方程“”的两根
1)求实数的值; 2)求的值.
18. (本题满分14分)
已知函数,R.
(1)求它的振幅、周期、初相;
(2)用五点法作出一个周期的简图;
(3)该函数的图象可由(R)的图象经过怎样的平移和伸缩变换得到?
19. (本题满分14分)
已知(其中)的图象与轴的交点中,相邻两个交点之间的距离为.若为图象上一个最低点.
(1)求的解析式;
(2)求函数图象的对称轴方程和对称中心坐标.
(3)已知求函数的值域.
20. (本题满分14分)
设函数,函数.且当时,恒成立,
1)当时,求不等式的解集;
2)求的最大值;
3)当m取最大值时,判断的奇偶性并给予证明.
东厦中学2011—2012学年度第一学期期末考试
高一级数学科试卷参考答案
一、选择题
CACDB DCAA D
二、填空题
11.1 12. 13. 14.②③
三、解答题
15. 解:∵角θ终边上一点,
由三角函数的定义可得:
∴
∴,
16. 解:(1)设直线OA的解析式为y=ax(0x15),依题意得,
把点A(15,27)代入得,15a=27 解得 a=1.8
则直线OA的解析式为y=1.8x(0x15)
设直线AB的解析式为y=a’x+b (x>15)
把点A(15,27)和点(20,39.5)代入得 解得
则直线AB的解析式为y=2.5x-10.5(x>15)
即 y=f(x)=
(2)当x=21时,y=2.521-10.5=42
若该用户用水21吨,则该用户需交水费42元。
17. 解:(1)是关于的方程的两根,
(2)原式=
18. 1、解:(1)函数的振幅为,周期为,初相为.
(2)列表:
0
0
0
画简图:
(3)解法1:
函数的图象 函数的图象,
函数的图象,
函数的图.
解法2:函数的图象
函数的图象 函数的图象
函数的图象.
19、(1)由题意知,所以,即,故,
又且,所以,,所以,
所以函数解析式是;
(2)令,得,
即函数图象的对称轴方程为;21世纪教育网
令,得,
(3),,,
所以函数的值域为
20.解:(1)当时,由解得,
故不等式的解集为.
配方得,,
∵时,恒成立,
即恒成立,
∴
令,对称轴为,
则,
∴,故的最大值为3.
由(2)知,,
由解得,故.
又,
∴
故是奇函数.
同课章节目录
