2022年高考数学复习专题课件 ★★六个超越函数的性质和应用 PPT(共56张PPT)
文档属性
| 名称 | 2022年高考数学复习专题课件 ★★六个超越函数的性质和应用 PPT(共56张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 14:54:16 | ||
图片预览









文档简介
(共56张PPT)
六个超越函数的性质和应用
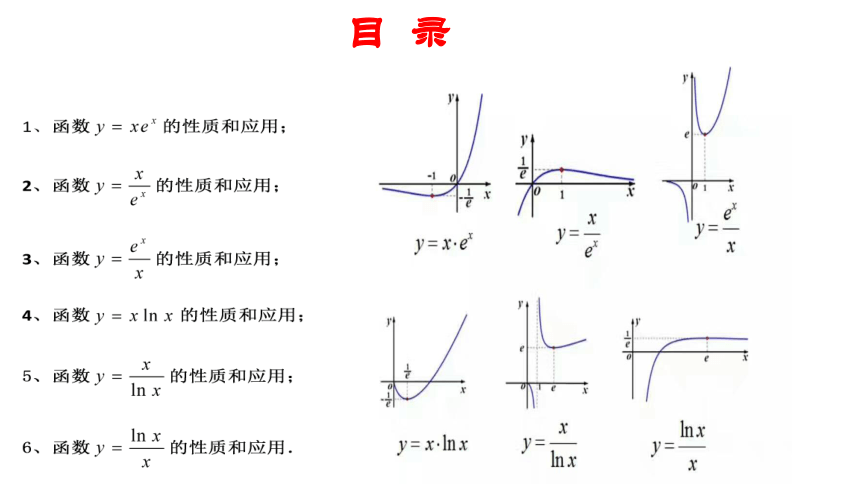
目 录
x
y
l
P
A
B
C
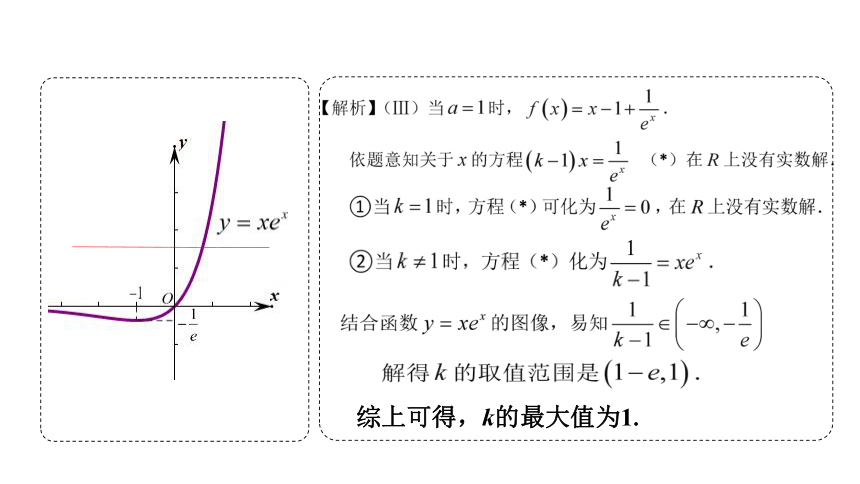
综上可得,k的最大值为1.
x
y
l
P
A
B
C
【针对训练1】已知函数
(1)若函数 f(x) 的最小值为 0 ,求 a 的值;
(2)证明不等式:
x
y
l
P
A
B
C
【评析】通常这种题,一定要寻找第一问与第二问之间的联系,这种联系常常成为解题的突破点.
x
y
l
P
A
B
C
x
y
l
P
A
B
C
x
y
l
P
A
B
C
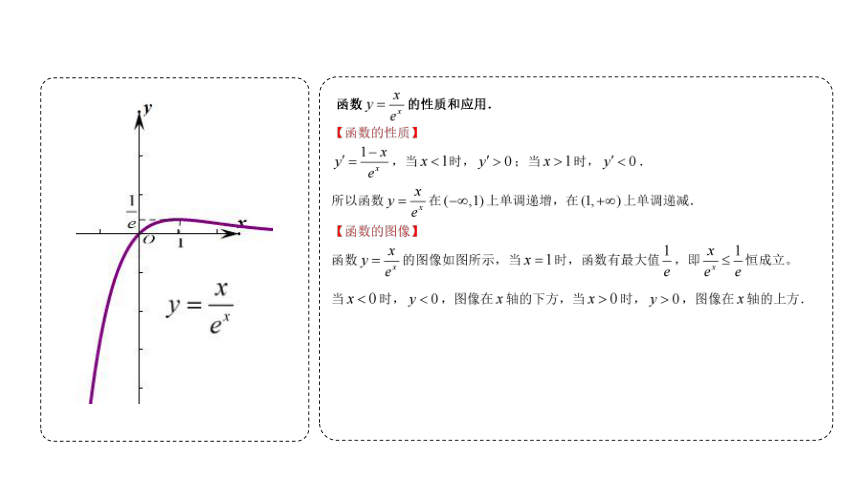
(这里是利用图像的直观印象,要给出证明,还需要利用单调性的定义严格证明)
结合(Ⅱ)和(Ⅲ),有哪些启示?
【分析】本题是函数的零点问题,难点是利用函数的单调性与零点存在定理判定零点的个数.
我们先来看看标准解答:
(2017年新课标I卷理21).
(2016年新课标I卷文21).
如出一辙
函数类似
问法相同
注意f(x)过了定点(1,0),即f(1)=0.
1
【评析】第三问巧妙地使用了前两问的结论,使得证明的过程得以简化.
【解析】(Ⅰ)略,
a=1,b=2
【分析】把 x 乘到括号里去,就会出现 xlnx,利用其最小值再放缩.
【分析】把 x 乘到括号里去,就会出现 xlnx,利用其最小值再放缩.
【分析】题目的本意是利用第一问的单调性证明第二问的不等式,而事实上可以利用函数y=xlnx的性质证第二问的不等式,再用这个不等式通过赋值比较第三问中三个数的大小.
【评析】像这种比较数字大小的题,通常都是在已有的不等式中,恰当地赋值就可以解决.
【例题1】(2017年高考新课标Ⅰ理科第11题)
【分析】由于x,y,z都在指数位置上,所以宜用取对数的办法将它们从指数位置上放下来.
【评析】本题在取对数后,也可采取作商比较法解决.
(III)将这6个数按时从小到大的顺序排序,并证明你的结论.
【分析】只需比较 与
, 与 的大小即可
【分析】
第一问,略;
第二问,可以考虑分离变量求a的取值范围;
第三问,可以考虑借助题干中的不等式证明要求证的不等式.
(2)若对任意的x>0,
求实数a的取值范围;
(2)若对任意的x>0,
求实数a的取值范围;
(3)求证:对任意的x>0,都有
(2)若对任意的x>0,
求实数a的取值范围;
(3)求证:对任意的x>0,都有
【评析】证明不等式实质就是应用不等式的传递性,可以采用同向不等式相加(如证法一),也可以层层传递(如证法二),也可以用叠乘等等.
【分析】
(1)略;
(2)讨论f(x)的零点个数,
可以转化为求 的交点个数.
六个超越函数的性质和应用
目 录
x
y
l
P
A
B
C
综上可得,k的最大值为1.
x
y
l
P
A
B
C
【针对训练1】已知函数
(1)若函数 f(x) 的最小值为 0 ,求 a 的值;
(2)证明不等式:
x
y
l
P
A
B
C
【评析】通常这种题,一定要寻找第一问与第二问之间的联系,这种联系常常成为解题的突破点.
x
y
l
P
A
B
C
x
y
l
P
A
B
C
x
y
l
P
A
B
C
(这里是利用图像的直观印象,要给出证明,还需要利用单调性的定义严格证明)
结合(Ⅱ)和(Ⅲ),有哪些启示?
【分析】本题是函数的零点问题,难点是利用函数的单调性与零点存在定理判定零点的个数.
我们先来看看标准解答:
(2017年新课标I卷理21).
(2016年新课标I卷文21).
如出一辙
函数类似
问法相同
注意f(x)过了定点(1,0),即f(1)=0.
1
【评析】第三问巧妙地使用了前两问的结论,使得证明的过程得以简化.
【解析】(Ⅰ)略,
a=1,b=2
【分析】把 x 乘到括号里去,就会出现 xlnx,利用其最小值再放缩.
【分析】把 x 乘到括号里去,就会出现 xlnx,利用其最小值再放缩.
【分析】题目的本意是利用第一问的单调性证明第二问的不等式,而事实上可以利用函数y=xlnx的性质证第二问的不等式,再用这个不等式通过赋值比较第三问中三个数的大小.
【评析】像这种比较数字大小的题,通常都是在已有的不等式中,恰当地赋值就可以解决.
【例题1】(2017年高考新课标Ⅰ理科第11题)
【分析】由于x,y,z都在指数位置上,所以宜用取对数的办法将它们从指数位置上放下来.
【评析】本题在取对数后,也可采取作商比较法解决.
(III)将这6个数按时从小到大的顺序排序,并证明你的结论.
【分析】只需比较 与
, 与 的大小即可
【分析】
第一问,略;
第二问,可以考虑分离变量求a的取值范围;
第三问,可以考虑借助题干中的不等式证明要求证的不等式.
(2)若对任意的x>0,
求实数a的取值范围;
(2)若对任意的x>0,
求实数a的取值范围;
(3)求证:对任意的x>0,都有
(2)若对任意的x>0,
求实数a的取值范围;
(3)求证:对任意的x>0,都有
【评析】证明不等式实质就是应用不等式的传递性,可以采用同向不等式相加(如证法一),也可以层层传递(如证法二),也可以用叠乘等等.
【分析】
(1)略;
(2)讨论f(x)的零点个数,
可以转化为求 的交点个数.
同课章节目录
