2019年高考数学真题及解析(北京卷:理科)
文档属性
| 名称 | 2019年高考数学真题及解析(北京卷:理科) |  | |
| 格式 | docx | ||
| 文件大小 | 550.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 15:52:10 | ||
图片预览




文档简介
2019年高考数学真题(北京卷:理科)
第一部分(选择题 共40分)
一、选择题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知复数z=2+i,则( )
(A) (B) (C)3 (D)5
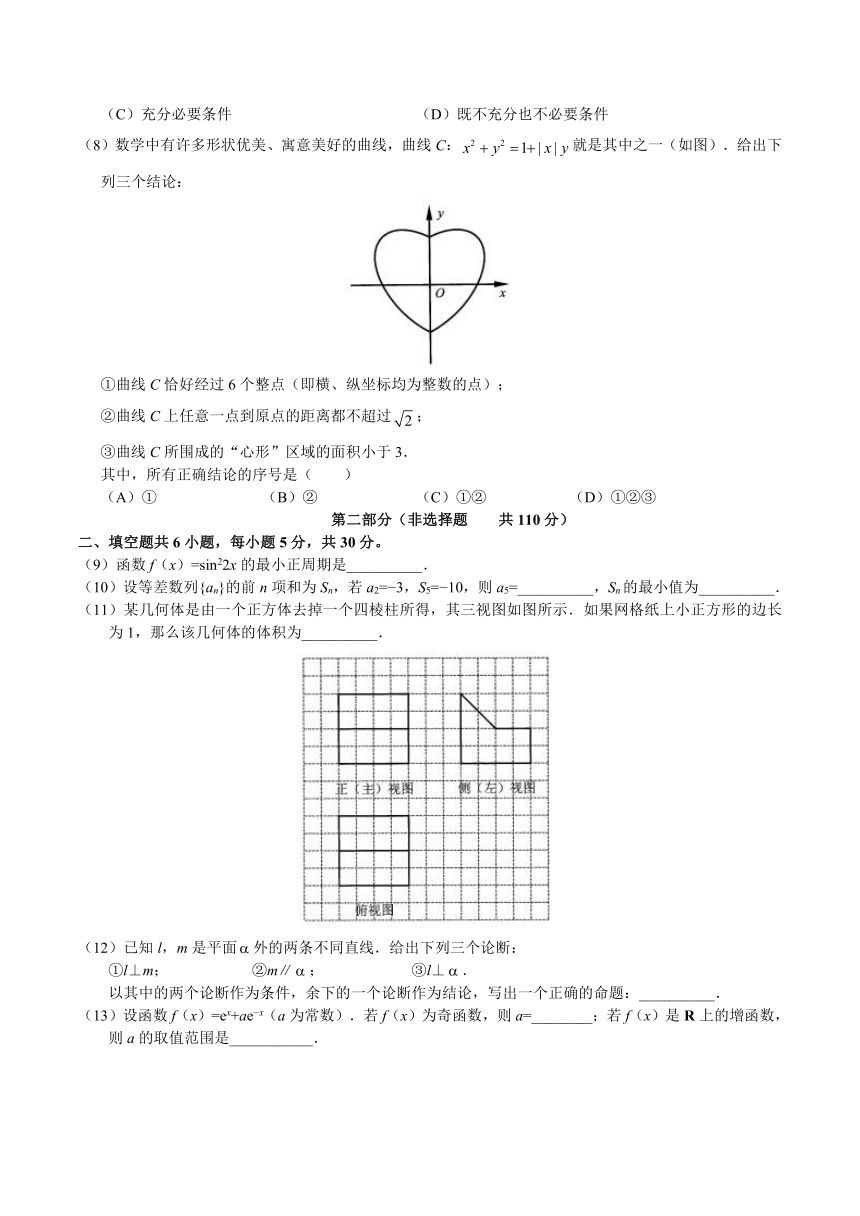
(2)执行如图所示的程序框图,输出的s值为( )
(A)1 (B)2 (C)3 (D)4
(3)已知直线l的参数方程为(t为参数),则点(1,0)到直线l的距离是( )
(A) (B) (C) (D)
(4)已知椭圆(a>b>0)的离心率为,则( )
(A)a2=2b2 (B)3a2=4b2 (C)a=2b (D)3a=4b
(5)若x,y满足,且y≥ 1,则3x+y的最大值为( )
(A) 7 (B)1 (C)5 (D)7
(6)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m2 m1=lg,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是 26.7,天狼星的星等是 1.45,则太阳与天狼星的亮度的比值为( )
(A)1010.1 (B)10.1 (C)lg10.1 (D)10 10.1
(7)设点A,B,C不共线,则“与的夹角为锐角”是“”的( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(8)数学中有许多形状优美、寓意美好的曲线,曲线C:就是其中之一(如图).给出下列三个结论:
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是( )
(A)① (B)② (C)①② (D)①②③
第二部分(非选择题 共110分)
二、填空题共6小题,每小题5分,共30分。
(9)函数f(x)=sin22x的最小正周期是__________.
(10)设等差数列{an}的前n项和为Sn,若a2= 3,S5= 10,则a5=__________,Sn的最小值为__________.
(11)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.
(12)已知l,m是平面外的两条不同直线.给出下列三个论断:
①l⊥m; ②m∥; ③l⊥.
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.
(13)设函数f(x)=ex+ae x(a为常数).若f(x)为奇函数,则a=________;若f(x)是R上的增函数,则a的取值范围是___________.
(14)李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
三、解答题共6小题,共80分。解答应写出文字说明,演算步骤或证明过程。
(15)(本小题13分)
在△ABC中,a=3,b c=2,cosB=.
(Ⅰ)求b,c的值;
(Ⅱ)求sin(B–C)的值.
(16)(本小题14分)
如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且.
(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)求二面角F–AE–P的余弦值;
(Ⅲ)设点G在PB上,且.判断直线AG是否在平面AEF内,说明理由.
(17)(本小题13分)
改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付金额(元) 支付方式 (0,1000] (1000,2000] 大于2000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
(18)(本小题14分)
已知抛物线C:x2= 2py经过点(2, 1).
(Ⅰ)求抛物线C的方程及其准线方程;
(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y= 1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.
(19)(本小题13分)
已知函数.
(Ⅰ)求曲线的斜率为1的切线方程;
(Ⅱ)当时,求证:;
(Ⅲ)设,记在区间上的最大值为M(a).当M(a)最小时,求a的值.
(20)(本小题13分)
已知数列{an},从中选取第i1项、第i2项、…、第im项(i1(Ⅰ)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;
(Ⅱ)已知数列{an}的长度为p的递增子列的末项的最小值为,长度为q的递增子列的末项的最小值为.若p(Ⅲ)设无穷数列{an}的各项均为正整数,且任意两项均不相等.若{an}的长度为s的递增子列末项的最小值为2s–1,且长度为s末项为2s–1的递增子列恰有2s-1个(s=1,2,…),求数列{an}的通项公式.
参考答案
一、选择题
(1)D 【解析】∵z=2+i,∴z =|z|2=()2=5.故选D.
(2)B 【解析】当第一步,k=1,s=1,则s=2,不满足条件k3,执行循环体;第二步,k=2,s=2,不满
足条件k3,执行循环体;第三步,k=3,s=2,此时,满足条件k3,退出循环,输出s的值
为2.故选B.
(3)D 【解析】由(t为参数),消去t,可得4x3y+2=0.则点(1,0)到直线l的距离是
d==.故选D.
(4)B 【解析】由题意,=,得==,∴4a24b2=a2,即3a2=4b2.故选B.
(5)C 【解析】由作出可行域如图,联立,解得A(2,1),令z=3x+y,则y=3x+z,
由图可知,直线在A处取最大值,为321=5.故选C.
(6)A 【解析】设太阳的星等是m1=26.7,天狼星的星等是m2=1.45,由题意可得,m2m1=
1.45(26.7)=lg,∴lg==10.1,∴=1010.1.故选A.
(7)C 【解析】点A,B,C不共线,“与的夹角为锐角” “|+|||”,“|+|||”
“|+|||” “(+)2()2” 0 与的夹
角为锐角,∴与的夹角为锐角是“|+|||”的充分必要条件,故选C.
(8)C 【解析】①将x换成x方程不变,所以图形关于y轴对称,当x=0时,代入得y2=1,∴y=1,
即曲线经过(0,1),(0,1);当x0时,方程变为y2xy+x21=0,所以=x24(x21)0,
解得x∈(0,],所以x只能取整数1,当x=1时,y2y=0,解得y=0或y=1,即曲线经过
(1,0),(1,1),根据对称性可得曲线还经过(1,0),(1,1),故曲线一共经过6
个整点,正确;②当x0时,由x2+y2=1+xy得x2+y21=xy,(当x=y时取等),∴
x2+y22,∴,即曲线C上y轴右边的点到原点的距离不超过,根据对称性可
得,曲线C上任意一点到原点的距离都不超过,正确;③在x轴上图形面积大于矩形面积
=12=2,x轴下方的面积大于等腰直角三角形的面积=21=1,因此曲线C所围成的“心形”
区域的面积大于2+1=3,错误.故选C.
二、填空题
(9) 【解析】∵f(x)=sin2(2x),∴f(x)=,∴f(x)的周期T==.
(10)0 【解析】 设等差数列{an}的前n项和为Sn,a2=3,S5=10,∴解得
∴a5=a1+4d=4+41=0,Sn=na1+d=4n+=(n)2,∴
n=4或n=5时,Sn为S4=S5最小,最小值为10.
(11)40 【解析】由题意可知,该几何体是一个长方体和一个三棱柱组合而成,则该几何体的体积
V=422+(2+4)24=40.
(12)若,,则.(答案不唯一) 【解析】由l,m是平面α外的两条不同直线可知,由
线面平行的判定定理得,若l⊥α,m∥α,则l⊥m.
(13) 【解析】根据题意,函数f(x)=ex+aex为奇函数,则f(x)=f(x),即
ex+aex=(ex+aex),变形可得a=1,函数f(x)=ex+aex,其导数f'(x)
=exaex,又∵f(x)是R上的增函数,则f(x)的导数f'(x)=exaex0
在R上恒成立,变形可得,ae2x恒成立,则a0,即a的取值范围为(∞,
0].
(14)130 15 【解析】①当x=10时,顾客一次购买草莓和西瓜各1盒,可得60+80=140(元),即有顾
客需要支付14010=130(元);②在促销活动中,设订单总金额为M元,可得
(Mx)80%M70%,即有x,由题意可得M120,可得x=15,则x的最
大值为15元.
三、解答题
(15)(共13分)
解:(Ⅰ)由余弦定理,得
.
∵,∴.
解得.∴.
(Ⅱ)由得.
由正弦定理得.
在中,∠B是钝角,
∴∠C为锐角.
∴.
∴.
(16)(共14分)
解:(Ⅰ)∵PA⊥平面ABCD,∴PA⊥CD.
又∵AD⊥CD,∴CD⊥平面PAD.
(Ⅱ)过A作AD的垂线交BC于点M.
∵PA⊥平面ABCD,∴PA⊥AM,PA⊥AD.
如图建立空间直角坐标系A-xyz,
则A(0,0,0),B(2,1,0),C(2,2,0),D(0,2,0),P(0,0,2).
∵E为PD的中点,所以E(0,1,1).
∴.
∴.
设平面AEF的法向量为n=(x,y,z),则
即
令z=1,则.
于是.
又∵平面PAD的法向量为p=(1,0,0),
∴.
由题知,二面角F-AE-P为锐角,所以其余弦值为.
(Ⅲ)直线AG在平面AEF内.
∵点G在PB上,且,
∴.
由(Ⅱ)知,平面AEF的法向量.
∴.
∴直线AG在平面AEF内.
(17)(共13分)
解:(Ⅰ)由题意知,样本中仅使用A的学生有18+9+3=30人,仅使用B的学生有10+14+1=25人,A,B两种支付方式都不使用的学生有5人.
故样本中A,B两种支付方式都使用的学生有100 30 25 5=40人.
所以从全校学生中随机抽取1人,该学生上个月A,B两种支付方式都使用的概率估计为.
(Ⅱ)X的所有可能值为0,1,2.
记事件C为“从样本仅使用A的学生中随机抽取1人,该学生上个月的支付金额大于1000元”,事件D为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于1000元”.
由题设知,事件C,D相互独立,且.
所以,
=0.4×(1 0.6)+(1 0.4)×0.6
=0.52,
.
所以X的分布列为
X 0 1 2
P 0.24 0.52 0.24
故X的数学期望E(X)=0×0.24+1×0.52+2×0.24=1.
(Ⅲ)记事件E为“从样本仅使用A的学生中随机抽查3人,他们本月的支付金额都大于2000元”.
假设样本仅使用A的学生中,本月支付金额大于2000元的人数没有变化,则由上个月的样本数据得.
答案示例1:可以认为有变化.理由如下:
P(E)比较小,概率比较小的事件一般不容易发生.一旦发生,就有理由认为本月的支付金额大于2000元的人数发生了变化.所以可以认为有变化.
答案示例2:无法确定有没有变化.理由如下:
事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的,所以无法确定有没有变化.
(18)(共14分)
解:(Ⅰ)由抛物线经过点,得.
∴抛物线的方程为,其准线方程为.
(Ⅱ)抛物线的焦点为.
设直线的方程为.
由得.
设,则.
直线的方程为.
令,得点A的横坐标.
同理得点B的横坐标.
设点,则,
.
令,即,则或.
综上,以AB为直径的圆经过y轴上的定点和.
(19)(共13分)
解:(Ⅰ)由得.
令,即,得或.
又,,
∴曲线的斜率为1的切线方程是与,
即与.
(Ⅱ)令.
由得.
令得或.
的情况如下:
∴的最小值为,最大值为.
故,即.
(Ⅲ)由(Ⅱ)知,
当时,;
当时,;
当时,.
综上,当最小时,.
(20)(共13分)
解:(Ⅰ)1,3,5,6.(答案不唯一)
(Ⅱ)设长度为q末项为的一个递增子列为.
由p∵的长度为p的递增子列末项的最小值为,
又∵是的长度为p的递增子列,
∴.∴·
(Ⅲ)由题设知,所有正奇数都是中的项.
先证明:若2m是中的项,则2m必排在2m 1之前(m为正整数).
假设2m排在2m 1之后.
设是数列的长度为m末项为2m 1的递增子列,
则是数列的长度为m+1末项为2m的递增子列.与已知矛盾.
再证明:所有正偶数都是中的项.
假设存在正偶数不是中的项,设不在中的最小的正偶数为2m.
∵2k排在2k 1之前(k=1,2,…,m 1),
∴2k和不可能在的同一个递增子列中.
又中不超过2m+1的数为1,2,…,2m 2,2m 1,2m+1,
∴的长度为m+1且末项为2m+1的递增子列个数至多为.
与已知矛盾.
最后证明:2m排在2m 3之后(m≥2为整数).
假设存在2m(m≥2),使得2m排在2m 3之前,
则的长度为m+1且末项为2m+l的递增子列的个数小于.与已知矛盾.
综上,数列只可能为2,1,4,3,…,2m 3,2m,2m 1,….
经验证,数列2,1,4,3,…,2m 3,2m,2m 1,…符合条件.
所以
第一部分(选择题 共40分)
一、选择题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知复数z=2+i,则( )
(A) (B) (C)3 (D)5
(2)执行如图所示的程序框图,输出的s值为( )
(A)1 (B)2 (C)3 (D)4
(3)已知直线l的参数方程为(t为参数),则点(1,0)到直线l的距离是( )
(A) (B) (C) (D)
(4)已知椭圆(a>b>0)的离心率为,则( )
(A)a2=2b2 (B)3a2=4b2 (C)a=2b (D)3a=4b
(5)若x,y满足,且y≥ 1,则3x+y的最大值为( )
(A) 7 (B)1 (C)5 (D)7
(6)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m2 m1=lg,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是 26.7,天狼星的星等是 1.45,则太阳与天狼星的亮度的比值为( )
(A)1010.1 (B)10.1 (C)lg10.1 (D)10 10.1
(7)设点A,B,C不共线,则“与的夹角为锐角”是“”的( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(8)数学中有许多形状优美、寓意美好的曲线,曲线C:就是其中之一(如图).给出下列三个结论:
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是( )
(A)① (B)② (C)①② (D)①②③
第二部分(非选择题 共110分)
二、填空题共6小题,每小题5分,共30分。
(9)函数f(x)=sin22x的最小正周期是__________.
(10)设等差数列{an}的前n项和为Sn,若a2= 3,S5= 10,则a5=__________,Sn的最小值为__________.
(11)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.
(12)已知l,m是平面外的两条不同直线.给出下列三个论断:
①l⊥m; ②m∥; ③l⊥.
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.
(13)设函数f(x)=ex+ae x(a为常数).若f(x)为奇函数,则a=________;若f(x)是R上的增函数,则a的取值范围是___________.
(14)李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
三、解答题共6小题,共80分。解答应写出文字说明,演算步骤或证明过程。
(15)(本小题13分)
在△ABC中,a=3,b c=2,cosB=.
(Ⅰ)求b,c的值;
(Ⅱ)求sin(B–C)的值.
(16)(本小题14分)
如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且.
(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)求二面角F–AE–P的余弦值;
(Ⅲ)设点G在PB上,且.判断直线AG是否在平面AEF内,说明理由.
(17)(本小题13分)
改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付金额(元) 支付方式 (0,1000] (1000,2000] 大于2000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
(18)(本小题14分)
已知抛物线C:x2= 2py经过点(2, 1).
(Ⅰ)求抛物线C的方程及其准线方程;
(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y= 1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.
(19)(本小题13分)
已知函数.
(Ⅰ)求曲线的斜率为1的切线方程;
(Ⅱ)当时,求证:;
(Ⅲ)设,记在区间上的最大值为M(a).当M(a)最小时,求a的值.
(20)(本小题13分)
已知数列{an},从中选取第i1项、第i2项、…、第im项(i1
(Ⅱ)已知数列{an}的长度为p的递增子列的末项的最小值为,长度为q的递增子列的末项的最小值为.若p
参考答案
一、选择题
(1)D 【解析】∵z=2+i,∴z =|z|2=()2=5.故选D.
(2)B 【解析】当第一步,k=1,s=1,则s=2,不满足条件k3,执行循环体;第二步,k=2,s=2,不满
足条件k3,执行循环体;第三步,k=3,s=2,此时,满足条件k3,退出循环,输出s的值
为2.故选B.
(3)D 【解析】由(t为参数),消去t,可得4x3y+2=0.则点(1,0)到直线l的距离是
d==.故选D.
(4)B 【解析】由题意,=,得==,∴4a24b2=a2,即3a2=4b2.故选B.
(5)C 【解析】由作出可行域如图,联立,解得A(2,1),令z=3x+y,则y=3x+z,
由图可知,直线在A处取最大值,为321=5.故选C.
(6)A 【解析】设太阳的星等是m1=26.7,天狼星的星等是m2=1.45,由题意可得,m2m1=
1.45(26.7)=lg,∴lg==10.1,∴=1010.1.故选A.
(7)C 【解析】点A,B,C不共线,“与的夹角为锐角” “|+|||”,“|+|||”
“|+|||” “(+)2()2” 0 与的夹
角为锐角,∴与的夹角为锐角是“|+|||”的充分必要条件,故选C.
(8)C 【解析】①将x换成x方程不变,所以图形关于y轴对称,当x=0时,代入得y2=1,∴y=1,
即曲线经过(0,1),(0,1);当x0时,方程变为y2xy+x21=0,所以=x24(x21)0,
解得x∈(0,],所以x只能取整数1,当x=1时,y2y=0,解得y=0或y=1,即曲线经过
(1,0),(1,1),根据对称性可得曲线还经过(1,0),(1,1),故曲线一共经过6
个整点,正确;②当x0时,由x2+y2=1+xy得x2+y21=xy,(当x=y时取等),∴
x2+y22,∴,即曲线C上y轴右边的点到原点的距离不超过,根据对称性可
得,曲线C上任意一点到原点的距离都不超过,正确;③在x轴上图形面积大于矩形面积
=12=2,x轴下方的面积大于等腰直角三角形的面积=21=1,因此曲线C所围成的“心形”
区域的面积大于2+1=3,错误.故选C.
二、填空题
(9) 【解析】∵f(x)=sin2(2x),∴f(x)=,∴f(x)的周期T==.
(10)0 【解析】 设等差数列{an}的前n项和为Sn,a2=3,S5=10,∴解得
∴a5=a1+4d=4+41=0,Sn=na1+d=4n+=(n)2,∴
n=4或n=5时,Sn为S4=S5最小,最小值为10.
(11)40 【解析】由题意可知,该几何体是一个长方体和一个三棱柱组合而成,则该几何体的体积
V=422+(2+4)24=40.
(12)若,,则.(答案不唯一) 【解析】由l,m是平面α外的两条不同直线可知,由
线面平行的判定定理得,若l⊥α,m∥α,则l⊥m.
(13) 【解析】根据题意,函数f(x)=ex+aex为奇函数,则f(x)=f(x),即
ex+aex=(ex+aex),变形可得a=1,函数f(x)=ex+aex,其导数f'(x)
=exaex,又∵f(x)是R上的增函数,则f(x)的导数f'(x)=exaex0
在R上恒成立,变形可得,ae2x恒成立,则a0,即a的取值范围为(∞,
0].
(14)130 15 【解析】①当x=10时,顾客一次购买草莓和西瓜各1盒,可得60+80=140(元),即有顾
客需要支付14010=130(元);②在促销活动中,设订单总金额为M元,可得
(Mx)80%M70%,即有x,由题意可得M120,可得x=15,则x的最
大值为15元.
三、解答题
(15)(共13分)
解:(Ⅰ)由余弦定理,得
.
∵,∴.
解得.∴.
(Ⅱ)由得.
由正弦定理得.
在中,∠B是钝角,
∴∠C为锐角.
∴.
∴.
(16)(共14分)
解:(Ⅰ)∵PA⊥平面ABCD,∴PA⊥CD.
又∵AD⊥CD,∴CD⊥平面PAD.
(Ⅱ)过A作AD的垂线交BC于点M.
∵PA⊥平面ABCD,∴PA⊥AM,PA⊥AD.
如图建立空间直角坐标系A-xyz,
则A(0,0,0),B(2,1,0),C(2,2,0),D(0,2,0),P(0,0,2).
∵E为PD的中点,所以E(0,1,1).
∴.
∴.
设平面AEF的法向量为n=(x,y,z),则
即
令z=1,则.
于是.
又∵平面PAD的法向量为p=(1,0,0),
∴.
由题知,二面角F-AE-P为锐角,所以其余弦值为.
(Ⅲ)直线AG在平面AEF内.
∵点G在PB上,且,
∴.
由(Ⅱ)知,平面AEF的法向量.
∴.
∴直线AG在平面AEF内.
(17)(共13分)
解:(Ⅰ)由题意知,样本中仅使用A的学生有18+9+3=30人,仅使用B的学生有10+14+1=25人,A,B两种支付方式都不使用的学生有5人.
故样本中A,B两种支付方式都使用的学生有100 30 25 5=40人.
所以从全校学生中随机抽取1人,该学生上个月A,B两种支付方式都使用的概率估计为.
(Ⅱ)X的所有可能值为0,1,2.
记事件C为“从样本仅使用A的学生中随机抽取1人,该学生上个月的支付金额大于1000元”,事件D为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于1000元”.
由题设知,事件C,D相互独立,且.
所以,
=0.4×(1 0.6)+(1 0.4)×0.6
=0.52,
.
所以X的分布列为
X 0 1 2
P 0.24 0.52 0.24
故X的数学期望E(X)=0×0.24+1×0.52+2×0.24=1.
(Ⅲ)记事件E为“从样本仅使用A的学生中随机抽查3人,他们本月的支付金额都大于2000元”.
假设样本仅使用A的学生中,本月支付金额大于2000元的人数没有变化,则由上个月的样本数据得.
答案示例1:可以认为有变化.理由如下:
P(E)比较小,概率比较小的事件一般不容易发生.一旦发生,就有理由认为本月的支付金额大于2000元的人数发生了变化.所以可以认为有变化.
答案示例2:无法确定有没有变化.理由如下:
事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的,所以无法确定有没有变化.
(18)(共14分)
解:(Ⅰ)由抛物线经过点,得.
∴抛物线的方程为,其准线方程为.
(Ⅱ)抛物线的焦点为.
设直线的方程为.
由得.
设,则.
直线的方程为.
令,得点A的横坐标.
同理得点B的横坐标.
设点,则,
.
令,即,则或.
综上,以AB为直径的圆经过y轴上的定点和.
(19)(共13分)
解:(Ⅰ)由得.
令,即,得或.
又,,
∴曲线的斜率为1的切线方程是与,
即与.
(Ⅱ)令.
由得.
令得或.
的情况如下:
∴的最小值为,最大值为.
故,即.
(Ⅲ)由(Ⅱ)知,
当时,;
当时,;
当时,.
综上,当最小时,.
(20)(共13分)
解:(Ⅰ)1,3,5,6.(答案不唯一)
(Ⅱ)设长度为q末项为的一个递增子列为.
由p
又∵是的长度为p的递增子列,
∴.∴·
(Ⅲ)由题设知,所有正奇数都是中的项.
先证明:若2m是中的项,则2m必排在2m 1之前(m为正整数).
假设2m排在2m 1之后.
设是数列的长度为m末项为2m 1的递增子列,
则是数列的长度为m+1末项为2m的递增子列.与已知矛盾.
再证明:所有正偶数都是中的项.
假设存在正偶数不是中的项,设不在中的最小的正偶数为2m.
∵2k排在2k 1之前(k=1,2,…,m 1),
∴2k和不可能在的同一个递增子列中.
又中不超过2m+1的数为1,2,…,2m 2,2m 1,2m+1,
∴的长度为m+1且末项为2m+1的递增子列个数至多为.
与已知矛盾.
最后证明:2m排在2m 3之后(m≥2为整数).
假设存在2m(m≥2),使得2m排在2m 3之前,
则的长度为m+1且末项为2m+l的递增子列的个数小于.与已知矛盾.
综上,数列只可能为2,1,4,3,…,2m 3,2m,2m 1,….
经验证,数列2,1,4,3,…,2m 3,2m,2m 1,…符合条件.
所以
同课章节目录
