2019年高考数学真题及解析(天津卷:理科)
文档属性
| 名称 | 2019年高考数学真题及解析(天津卷:理科) | 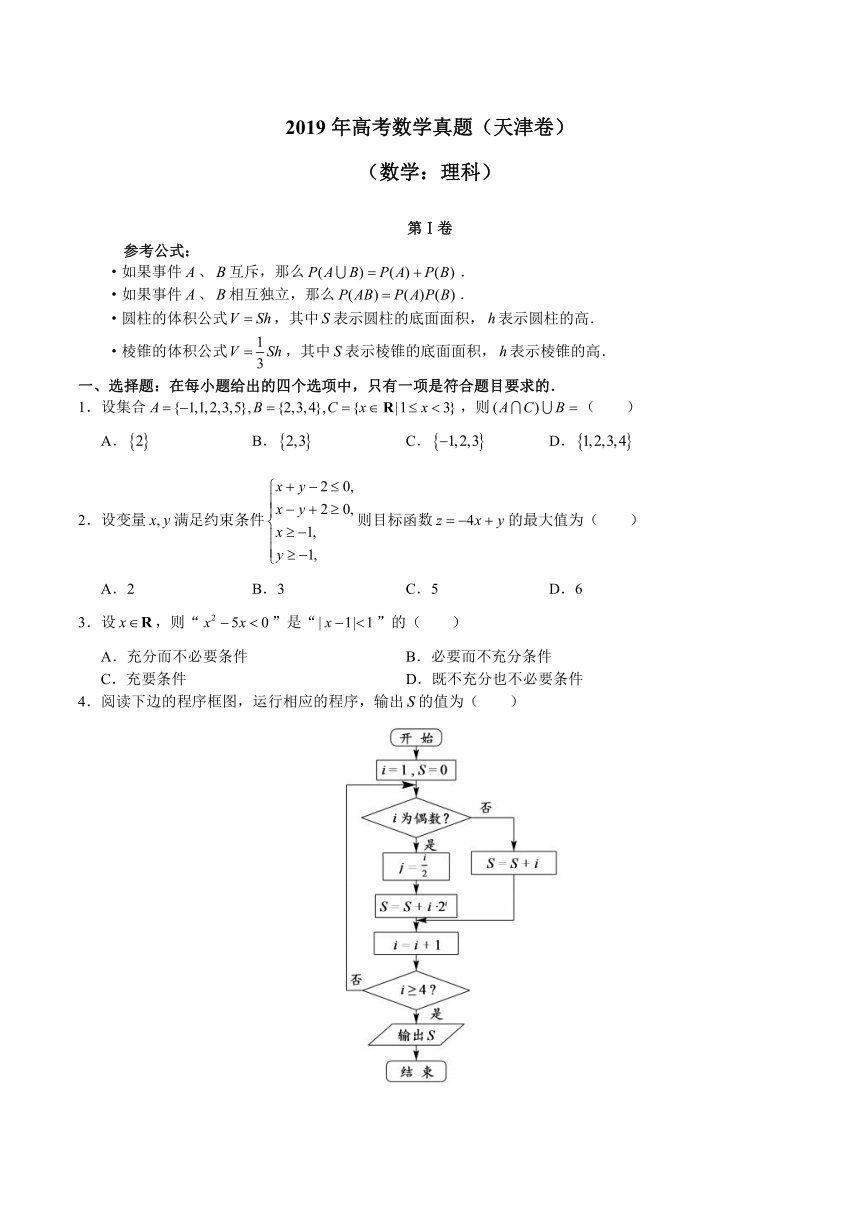 | |
| 格式 | docx | ||
| 文件大小 | 795.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 15:52:10 | ||
图片预览





文档简介
2019年高考数学真题(天津卷)
(数学:理科)
第Ⅰ卷
参考公式:
·如果事件、互斥,那么.
·如果事件、相互独立,那么.
·圆柱的体积公式,其中表示圆柱的底面面积,表示圆柱的高.
·棱锥的体积公式,其中表示棱锥的底面面积,表示棱锥的高.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则( )
A. B. C. D.
2.设变量满足约束条件则目标函数的最大值为( )
A.2 B.3 C.5 D.6
3.设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
4.阅读下边的程序框图,运行相应的程序,输出的值为( )
A.5 B.8 C.24 D.29
5.已知抛物线的焦点为,准线为,若与双曲线的两条渐近线分别交于点和点,且(为原点),则双曲线的离心率为( )
A. B. C. D.
6.已知,,,则的大小关系为( )
A. B. C. D.
7.已知函数是奇函数,将的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为.若的最小正周期为,且,则( )
A. B. C. D.
8.已知,设函数若关于的不等式在上恒成立,则的取值范围为( )
A. B. C. D.
第Ⅱ卷
二.填空题:本大题共6小题,每小题5分,共30分.
9.是虚数单位,则的值为_____________.
10.的展开式中的常数项为_____________.
11.已知四棱锥的底面是边长为的正方形,侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.
12.设,直线和圆(为参数)相切,则的值为_____________.
13.设,则的最小值为_____________.
14.在四边形中,,点在线段的延长线上,且,则_____________.
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分13分)
在中,内角所对的边分别为.已知,.
(Ⅰ)求的值;
(Ⅱ)求的值.
16.(本小题满分13分)
设甲、乙两位同学上学期间,每天7:30之前到校的概率均为.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量的分布列和数学期望;
(Ⅱ)设为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件发生的概率.
17.(本小题满分13分)
如图,平面,,.
(Ⅰ)求证:平面;
(Ⅱ)求直线与平面所成角的正弦值;
(Ⅲ)若二面角的余弦值为,求线段的长.
18.(本小题满分13分)
设椭圆的左焦点为,上顶点为.已知椭圆的短轴长为4,离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点在椭圆上,且异于椭圆的上、下顶点,点为直线与轴的交点,点在轴的负半轴上.若(为原点),且,求直线的斜率.
19.(本小题满分14分)
设是等差数列,是等比数列.已知.
(Ⅰ)求和的通项公式;
(Ⅱ)设数列满足其中.
(i)求数列的通项公式;
(ii)求.
20.(本小题满分14分)
设函数为的导函数.
(Ⅰ)求的单调区间;
(Ⅱ)当时,证明;
(Ⅲ)设为函数在区间内的零点,其中,证明.
参考答案
一.选择题
1.D 【解析】设集合A={1,1,2,3,5},集合C={x∈R|1x3},则集合A∩C={1,2},∵集合B={2,
3,4},则集合(A∩C)∪B={1,2}∪{2,3,4}={1,2,3,4};故选D.
2.C 【解析】由约束条件得可行域,由下图表示,联立解得A(1,1),
化目标函数z=4x+y为y=4x+z,由图可知,当直线y=4x+z过A时,z取最大值,=4+1=5.故
选C.
3.B 【解析】由x25x0可推出0x5,∵|x1|1,∴0x2,∵充分性:0x5推不出0x2,
充分性不成立;必要性:0x2 0x5,必要性成立,∴0x5是0x2的必要不充分条件,
即x25x0是|x1|1的必要不充分条件.故选B.
4.B 【解析】初始:i=1,s=0;第一次循环后,S=1,i=2,不满足条件;第二循环后,j=1,S=5,i=3,
不满足条件;第三次循环后,S=8,i=4,满足退出循环的条件;故输出S值为8,故选B.
5.D 【解析】∵抛物线y2=4x的焦点为F(1,0),准线为l:x=1,且l与双曲线=1(a0,
b0)的两条渐近线分别交于点A和点B,且|AB|=4|OF|=4(O为原点),∴|AB|=,|OF|=1,∴
=4,∴b=2a,∴c==a,∴e==.故选D.
6.A 【解析】由题意,可知:0a=log52=,b=log0.50.2===log25log24=2,
c=0.50.21,∴b最大,a、c都小于1.且ac,∴acb.故选A.
7.C 【解析】∵f(x)是奇函数,∴f(0)=0,即sinφ=0,|φ|,∴φ=0,则f(x)横坐标伸长到原来
的2倍(纵坐标不变),得到g(x).即g(x)=Asin(ωx)∵g(x)的最小正周期为2π,∴=2π,
得ω=2,则g(x)=Asinx,f(x)=Asin2x,若g()=,则g()=Asin=A=,即
A=2,则f(x)=2sin2x,则f()=2sin(2)=2sin=2=,故选C.
8.C 【解析】当x1时,f(x)=x22ax+2a0恒成立;则f(x)=x22ax+2a0 2a恒成立,
令h(x)=====
=0,∴2ah(x)max=0,∴a0.当x1时,f(x)=xalnx0 a恒
成立,令g(x)=,则g'(x)==,当xe时,g'(x)0,g(x)递增,当
1xe时,g'(x)0,g(x)递减,∴x=e时,g(x)取得最小值g(e)=e,∴ag(x)min=e,
综上a的取值范围是[0,e].故选C.
二.填空题
9. 【解析】由题意,得===23i,∴||=|23i|==.
10. 【解析】由题意,可知,此二项式的展开式的通项为Tr+1=(2x)8-r()r= 28-r ()r x8-r
()r= (1)r28-4r x8-4r.∴当84r=0,即r=2时,此时常数项T2+1= (1)228-4×2=28.
11. 【解析】由题可知,四棱锥底面是边长为的正方形,且对角线垂直相交平分,∴对角线长为2,
由勾股定理得,正四棱锥的高为=2,由于圆柱的一个底面的圆周经过四棱锥四条侧棱的中
点,有圆柱的上底面直径为底面正方形对角线的一半等于1,即半径等于;由相似比可得圆柱的
高为正四棱锥高的一半等于1,则圆柱的体积为V=sh=π()21=.
12. 【解析】∵a∈R,直线axy+2=0和圆(θ为参数)相切,∴圆心(2,1)到直线
axy+2=0的距离r==2,解得a=.
13. 【解析】x0,y0,x+2y=5,则===2+;由基
本不等式有2+2=4;当且仅当2=时,即xy=3,x+2y=5
时,即x=3,y=1或x=2,时,等号成立,故的最小值为4.
14. 【解析】∵AE=BE,AD∥BC,∠A=30°,∴在等腰三角形ABE中,∠BEA=120°,又AB=2,
∴AE=2,∴=,∵=+,∴=,又=++,
∴ =(+) ()=+ =+ cosA
=12+5225=1.
三.解答题
15.(13分)
(Ⅰ)解:在中,由正弦定理,得,
又∵,
∴,即.
又∵,
∴,.
由余弦定理可得.
(Ⅱ)解:由(Ⅰ)可得,
∴,
,
∴.
16.(13分)
(Ⅰ)解:因为甲同学上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为,故,从而.
∴随机变量的分布列为
0 1 2 3
随机变量的数学期望.
(Ⅱ)解:设乙同学上学期间的三天中7:30之前到校的天数为,
则,且.
由题意知事件与互斥,
且事件与,事件与均相互独立,
从而由(Ⅰ)知
.
17.(13分)
依题意,可以建立以为原点,分别以的方向为轴,轴,轴正方向的空间直角坐标系(如图),可得,.设,则.
(Ⅰ)证明:依题意,是平面的法向量,
又,
∴,
又∵直线平面,
∴平面.
(Ⅱ)解:依题意,.
设为平面的法向量,
则即不妨令,
可得.
∴.
∴直线与平面所成角的正弦值为.
(Ⅲ)解:设为平面的法向量,
则即
不妨令,可得.
由题意,有,
解得.经检验,符合题意.
∴线段的长为.
18.(13分)
(Ⅰ)解:设椭圆的半焦距为,依题意,,
又∵,可得,.
∴椭圆的方程为.
(Ⅱ)解:由题意,设.
设直线的斜率为,又,
则直线的方程为,
与椭圆方程联立
整理得,
可得,代入得,
进而直线的斜率.
在中,令,得.
由题意得,
∴直线的斜率为.
由,得,
化简得,从而.
∴直线的斜率为或.
19.(14分)
(Ⅰ)解:设等差数列的公差为,等比数列的公比为.
依题意得解得
故.
∴的通项公式为的通项公式为.
(Ⅱ)(i)解:.
∴数列的通项公式为.
(ii)解:
.
20.(14分)
(Ⅰ)解:由已知,有.
∴当时,有,得,则单调递减;
当时,有,得,则单调递增.
∴的单调递增区间为,
的单调递减区间为.
(Ⅱ)证明:记.
依题意及(Ⅰ),有,
∴.
当时,,
故.
∴在区间上单调递减,
进而.
∴当时,.
(Ⅲ)证明:依题意,,即.
记,则,
且.
由及(Ⅰ),得.
由(Ⅱ)知,当时,,
∴在上为减函数,
∴.
又由(Ⅱ)知,,
故.
∴.
(数学:理科)
第Ⅰ卷
参考公式:
·如果事件、互斥,那么.
·如果事件、相互独立,那么.
·圆柱的体积公式,其中表示圆柱的底面面积,表示圆柱的高.
·棱锥的体积公式,其中表示棱锥的底面面积,表示棱锥的高.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则( )
A. B. C. D.
2.设变量满足约束条件则目标函数的最大值为( )
A.2 B.3 C.5 D.6
3.设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
4.阅读下边的程序框图,运行相应的程序,输出的值为( )
A.5 B.8 C.24 D.29
5.已知抛物线的焦点为,准线为,若与双曲线的两条渐近线分别交于点和点,且(为原点),则双曲线的离心率为( )
A. B. C. D.
6.已知,,,则的大小关系为( )
A. B. C. D.
7.已知函数是奇函数,将的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为.若的最小正周期为,且,则( )
A. B. C. D.
8.已知,设函数若关于的不等式在上恒成立,则的取值范围为( )
A. B. C. D.
第Ⅱ卷
二.填空题:本大题共6小题,每小题5分,共30分.
9.是虚数单位,则的值为_____________.
10.的展开式中的常数项为_____________.
11.已知四棱锥的底面是边长为的正方形,侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.
12.设,直线和圆(为参数)相切,则的值为_____________.
13.设,则的最小值为_____________.
14.在四边形中,,点在线段的延长线上,且,则_____________.
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分13分)
在中,内角所对的边分别为.已知,.
(Ⅰ)求的值;
(Ⅱ)求的值.
16.(本小题满分13分)
设甲、乙两位同学上学期间,每天7:30之前到校的概率均为.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量的分布列和数学期望;
(Ⅱ)设为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件发生的概率.
17.(本小题满分13分)
如图,平面,,.
(Ⅰ)求证:平面;
(Ⅱ)求直线与平面所成角的正弦值;
(Ⅲ)若二面角的余弦值为,求线段的长.
18.(本小题满分13分)
设椭圆的左焦点为,上顶点为.已知椭圆的短轴长为4,离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点在椭圆上,且异于椭圆的上、下顶点,点为直线与轴的交点,点在轴的负半轴上.若(为原点),且,求直线的斜率.
19.(本小题满分14分)
设是等差数列,是等比数列.已知.
(Ⅰ)求和的通项公式;
(Ⅱ)设数列满足其中.
(i)求数列的通项公式;
(ii)求.
20.(本小题满分14分)
设函数为的导函数.
(Ⅰ)求的单调区间;
(Ⅱ)当时,证明;
(Ⅲ)设为函数在区间内的零点,其中,证明.
参考答案
一.选择题
1.D 【解析】设集合A={1,1,2,3,5},集合C={x∈R|1x3},则集合A∩C={1,2},∵集合B={2,
3,4},则集合(A∩C)∪B={1,2}∪{2,3,4}={1,2,3,4};故选D.
2.C 【解析】由约束条件得可行域,由下图表示,联立解得A(1,1),
化目标函数z=4x+y为y=4x+z,由图可知,当直线y=4x+z过A时,z取最大值,=4+1=5.故
选C.
3.B 【解析】由x25x0可推出0x5,∵|x1|1,∴0x2,∵充分性:0x5推不出0x2,
充分性不成立;必要性:0x2 0x5,必要性成立,∴0x5是0x2的必要不充分条件,
即x25x0是|x1|1的必要不充分条件.故选B.
4.B 【解析】初始:i=1,s=0;第一次循环后,S=1,i=2,不满足条件;第二循环后,j=1,S=5,i=3,
不满足条件;第三次循环后,S=8,i=4,满足退出循环的条件;故输出S值为8,故选B.
5.D 【解析】∵抛物线y2=4x的焦点为F(1,0),准线为l:x=1,且l与双曲线=1(a0,
b0)的两条渐近线分别交于点A和点B,且|AB|=4|OF|=4(O为原点),∴|AB|=,|OF|=1,∴
=4,∴b=2a,∴c==a,∴e==.故选D.
6.A 【解析】由题意,可知:0a=log52=,b=log0.50.2===log25log24=2,
c=0.50.21,∴b最大,a、c都小于1.且ac,∴acb.故选A.
7.C 【解析】∵f(x)是奇函数,∴f(0)=0,即sinφ=0,|φ|,∴φ=0,则f(x)横坐标伸长到原来
的2倍(纵坐标不变),得到g(x).即g(x)=Asin(ωx)∵g(x)的最小正周期为2π,∴=2π,
得ω=2,则g(x)=Asinx,f(x)=Asin2x,若g()=,则g()=Asin=A=,即
A=2,则f(x)=2sin2x,则f()=2sin(2)=2sin=2=,故选C.
8.C 【解析】当x1时,f(x)=x22ax+2a0恒成立;则f(x)=x22ax+2a0 2a恒成立,
令h(x)=====
=0,∴2ah(x)max=0,∴a0.当x1时,f(x)=xalnx0 a恒
成立,令g(x)=,则g'(x)==,当xe时,g'(x)0,g(x)递增,当
1xe时,g'(x)0,g(x)递减,∴x=e时,g(x)取得最小值g(e)=e,∴ag(x)min=e,
综上a的取值范围是[0,e].故选C.
二.填空题
9. 【解析】由题意,得===23i,∴||=|23i|==.
10. 【解析】由题意,可知,此二项式的展开式的通项为Tr+1=(2x)8-r()r= 28-r ()r x8-r
()r= (1)r28-4r x8-4r.∴当84r=0,即r=2时,此时常数项T2+1= (1)228-4×2=28.
11. 【解析】由题可知,四棱锥底面是边长为的正方形,且对角线垂直相交平分,∴对角线长为2,
由勾股定理得,正四棱锥的高为=2,由于圆柱的一个底面的圆周经过四棱锥四条侧棱的中
点,有圆柱的上底面直径为底面正方形对角线的一半等于1,即半径等于;由相似比可得圆柱的
高为正四棱锥高的一半等于1,则圆柱的体积为V=sh=π()21=.
12. 【解析】∵a∈R,直线axy+2=0和圆(θ为参数)相切,∴圆心(2,1)到直线
axy+2=0的距离r==2,解得a=.
13. 【解析】x0,y0,x+2y=5,则===2+;由基
本不等式有2+2=4;当且仅当2=时,即xy=3,x+2y=5
时,即x=3,y=1或x=2,时,等号成立,故的最小值为4.
14. 【解析】∵AE=BE,AD∥BC,∠A=30°,∴在等腰三角形ABE中,∠BEA=120°,又AB=2,
∴AE=2,∴=,∵=+,∴=,又=++,
∴ =(+) ()=+ =+ cosA
=12+5225=1.
三.解答题
15.(13分)
(Ⅰ)解:在中,由正弦定理,得,
又∵,
∴,即.
又∵,
∴,.
由余弦定理可得.
(Ⅱ)解:由(Ⅰ)可得,
∴,
,
∴.
16.(13分)
(Ⅰ)解:因为甲同学上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为,故,从而.
∴随机变量的分布列为
0 1 2 3
随机变量的数学期望.
(Ⅱ)解:设乙同学上学期间的三天中7:30之前到校的天数为,
则,且.
由题意知事件与互斥,
且事件与,事件与均相互独立,
从而由(Ⅰ)知
.
17.(13分)
依题意,可以建立以为原点,分别以的方向为轴,轴,轴正方向的空间直角坐标系(如图),可得,.设,则.
(Ⅰ)证明:依题意,是平面的法向量,
又,
∴,
又∵直线平面,
∴平面.
(Ⅱ)解:依题意,.
设为平面的法向量,
则即不妨令,
可得.
∴.
∴直线与平面所成角的正弦值为.
(Ⅲ)解:设为平面的法向量,
则即
不妨令,可得.
由题意,有,
解得.经检验,符合题意.
∴线段的长为.
18.(13分)
(Ⅰ)解:设椭圆的半焦距为,依题意,,
又∵,可得,.
∴椭圆的方程为.
(Ⅱ)解:由题意,设.
设直线的斜率为,又,
则直线的方程为,
与椭圆方程联立
整理得,
可得,代入得,
进而直线的斜率.
在中,令,得.
由题意得,
∴直线的斜率为.
由,得,
化简得,从而.
∴直线的斜率为或.
19.(14分)
(Ⅰ)解:设等差数列的公差为,等比数列的公比为.
依题意得解得
故.
∴的通项公式为的通项公式为.
(Ⅱ)(i)解:.
∴数列的通项公式为.
(ii)解:
.
20.(14分)
(Ⅰ)解:由已知,有.
∴当时,有,得,则单调递减;
当时,有,得,则单调递增.
∴的单调递增区间为,
的单调递减区间为.
(Ⅱ)证明:记.
依题意及(Ⅰ),有,
∴.
当时,,
故.
∴在区间上单调递减,
进而.
∴当时,.
(Ⅲ)证明:依题意,,即.
记,则,
且.
由及(Ⅰ),得.
由(Ⅱ)知,当时,,
∴在上为减函数,
∴.
又由(Ⅱ)知,,
故.
∴.
同课章节目录
