2022届高三数学二轮复习小专题:第三讲 随机抽样、用样本估计总体课件(共35张PPT)
文档属性
| 名称 | 2022届高三数学二轮复习小专题:第三讲 随机抽样、用样本估计总体课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 956.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 20:28:19 | ||
图片预览











文档简介
(共35张PPT)
第三讲 随机抽样、用样本估计总体
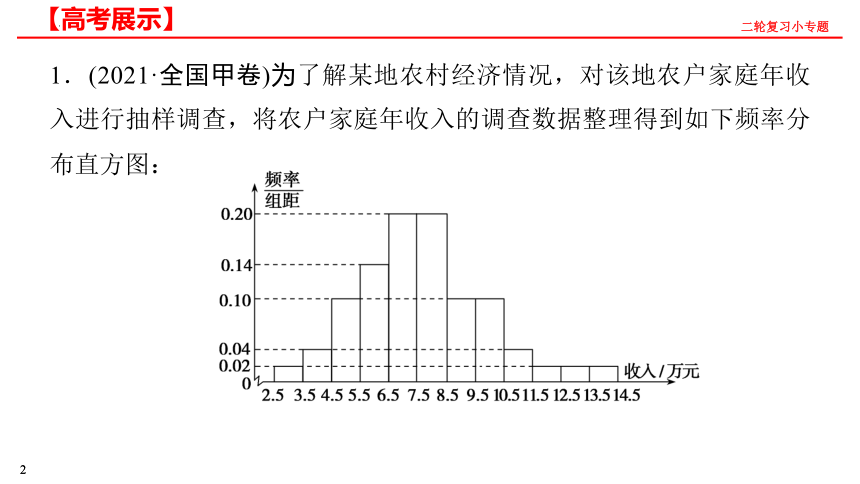
1.(2021·全国甲卷)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
【高考展示】
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
解析:对于A,根据频率分布直方图可知,家庭年收入低于4.5万元的农户比率约为(0.02+0.04)×1×100%=6%,故A正确;对于B,根据频率分布直方图可知,家庭年收入不低于10.5万元的农户比率约为(0.04+0.02+0.02+0.02)×1×100%=10%,故B正确;对于C,根据频率分布直方图可知,该地农户家庭年收入的平均值约为3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68(万元),故C错误;对于D,根据频率分布直方图可知,家庭年收入介于4.5万元至8.5万元之间的农户比率约为(0.10+0.14+0.20+0.20)×1×100%=64%>50%,故D正确.
答案:C
2.(2021·新高考全国Ⅰ卷)(多选题)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
CD
角度1 简单随机抽样
1.“嫦娥”五号的成功发射,实现了中国航天史上的五个“首次”,某中学为此举行了“讲好航天故事”演讲比赛.若将报名的30位同学编号为01,02,…,30,利用下面的随机数表来决定他们的出场顺序,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,重复的跳过,则选出来的第7个个体的编号为( )
45 67 32 12 12 31 02 01 04 52 15 20 01 12 51 29 32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A.12 B.20 C.29 D.23
C
【考点示例】
解析:依次从数表中读出的有效编号为:12,02,01,04,15,20,01,29,得到选出来的第7个个体的编号为29.
角度2 分层随机抽样
2.我国古代数学名著《九章算术》有一抽样问题:“今有北乡若干人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百零八人,问北乡人数几何?”其意思为:今有某地北面若干人,西面有7 488人,南面有6 912人,这三面要征调300人,而北面共征调108人(用分层随机抽样的方法),则北面共有多少人( )
A.8 000 B.8 100 C.8 200 D.8 300
B
3.从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图.
(1)直方图中x的值为________;
0.004 4
解析 由频率分布直方图知数据落在[200,250)内的频率为
1-(0.002 4+0.003 6+0.006 0+0.002 4+0.001 2)×50=0.22,
于是x= =0.004 4.
(2)在这些用户中,月用电量落在区间[100,250)内的户数为________.
70
解析 因为数据落在[100,250)内的频率为:
(0.003 6+0.006 0+0.004 4)×50=0.7,
所以所求户数为0.7×100=70.
角度4 折线图的应用
2.机器人是一种能够半自主或全自主工作的智能机器.它可以辅助甚至替代人类完成某些工作,提高工作效率,服务人类生活,扩大或延伸人的活动及能力范畴.某公司为了研究某机器人的销售情况,统计了2020年2月至7月M,N两店每月该机器人的营业额(单位:万元),得到如图所示的折线图,则下列说法中错误的是( )
A.N店营业额的平均值是29
B.M店营业额的平均值在[34,35]内
C.N店营业额总体呈上升趋势
D.M店营业额的极差比N店营业额的极差大
D
角度5 总体百分位数的估计
3.对某种电子元件使用寿命跟踪调查,所得样本的频率分布直方图如图所示.由图可知,这一批电子元件中寿命的85%分位数为____ h.
答案:500
角度6 总体集中、离散趋势的估计
4.教育部、发展改革委、财政部、体育总局《关于进一步加强学校体育工作的若干意见》中指出:把提高学生体质健康水平作为落实教育规划纲要和办好人民满意教育的重要任务.某中学对2021年秋季入学的高一年级学生身高进行调查.采用样本量比例分配的分层随机抽样,如果不知道样本数据,只知道抽取了男生23人,其平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分别为160.6和38.62,由此估计高一年级学生身高的平均数为__________,总体方差为__________.
答案:165.2 51.486 2
1.众数、中位数、平均数与直方图的关系
(1)众数为频率分布直方图中最高矩形的底边中点的横坐标.
(2)中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.
(3)平均数等于频率分布直方图中每个小矩形的面积乘小矩形底边中点的横坐标之和.
2.方差的计算与含义
计算方差首先要计算平均数,再按照方差的计算公式进行计算,方差和标准差是描述一个样本和总体的波动大小的特征数,方差、标准差越大说明波动越大.
1.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2019年9月到2020年2月这半年中,某个关键词的搜索指数变化的走势图.
【巩固训练】
根据该走势图,下列结论正确的是( )
A.这半年中,网民对该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D.从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
解析:根据走势图可知,这半年中,网民对该关键词相关的信息关注度不呈周期性变化,A错;这半年中,网民对该关键词相关的信息关注度增减不确定,B错;从网民对该关键词的搜索指数来看,去年10月份的搜索指数的稳定性小于11月份的搜索指数的稳定性,所以去年10月份的方差大于11月份的方差,C错;从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值,D正确.
答案:D
2.数据组87,86,90,82,83,85,88,80,79,90的方差为__________,第80百分位数为__________.
答案:13.8 89
3.某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1∶2∶1,用分层随机抽样的方法从3个分厂生产的电子产品中共抽取100件进行使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的平均使用寿命分别为980 h,1 020 h,1 032 h,则抽取的100件产品的平均使用寿命为
A.1 013 h B.1 014 h C.1 016 h D.1 022 h
√
解析 方法一 由分层随机抽样的知识可知,从第一、二、三分厂抽取的电子产品数量分别为25件,50件,25件,
则抽取的100件产品的平均使用寿命为
方法二 因为第一、二、三分厂的产量之比为1∶2∶1,
所以可以根据各层抽取数量所占的比例计算抽取的100件产品的平均使
用寿命为
5.(2019·全国Ⅱ)某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y的分组 [-0.20,0) [0,0.20) [0.20,0.40) [0.40,0.60) [0.60,0.80]
企业数 2 24 53 14 7
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
解:根据产值增长率频数分布表得,所调查的100个企业中产值增长率不低于40%的企业频率为 =0.21.
用样本频率分布估计总体分布得这类企业中产值增长率不低于40%的企业比例为21%,产值负增长的企业比例为2%.
=0.029 6,
所以,这类企业产值增长率的平均数与标准差的估计值分别为0.30,0.17.
第三讲 随机抽样、用样本估计总体
1.(2021·全国甲卷)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
【高考展示】
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
解析:对于A,根据频率分布直方图可知,家庭年收入低于4.5万元的农户比率约为(0.02+0.04)×1×100%=6%,故A正确;对于B,根据频率分布直方图可知,家庭年收入不低于10.5万元的农户比率约为(0.04+0.02+0.02+0.02)×1×100%=10%,故B正确;对于C,根据频率分布直方图可知,该地农户家庭年收入的平均值约为3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68(万元),故C错误;对于D,根据频率分布直方图可知,家庭年收入介于4.5万元至8.5万元之间的农户比率约为(0.10+0.14+0.20+0.20)×1×100%=64%>50%,故D正确.
答案:C
2.(2021·新高考全国Ⅰ卷)(多选题)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
CD
角度1 简单随机抽样
1.“嫦娥”五号的成功发射,实现了中国航天史上的五个“首次”,某中学为此举行了“讲好航天故事”演讲比赛.若将报名的30位同学编号为01,02,…,30,利用下面的随机数表来决定他们的出场顺序,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,重复的跳过,则选出来的第7个个体的编号为( )
45 67 32 12 12 31 02 01 04 52 15 20 01 12 51 29 32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A.12 B.20 C.29 D.23
C
【考点示例】
解析:依次从数表中读出的有效编号为:12,02,01,04,15,20,01,29,得到选出来的第7个个体的编号为29.
角度2 分层随机抽样
2.我国古代数学名著《九章算术》有一抽样问题:“今有北乡若干人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百零八人,问北乡人数几何?”其意思为:今有某地北面若干人,西面有7 488人,南面有6 912人,这三面要征调300人,而北面共征调108人(用分层随机抽样的方法),则北面共有多少人( )
A.8 000 B.8 100 C.8 200 D.8 300
B
3.从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图.
(1)直方图中x的值为________;
0.004 4
解析 由频率分布直方图知数据落在[200,250)内的频率为
1-(0.002 4+0.003 6+0.006 0+0.002 4+0.001 2)×50=0.22,
于是x= =0.004 4.
(2)在这些用户中,月用电量落在区间[100,250)内的户数为________.
70
解析 因为数据落在[100,250)内的频率为:
(0.003 6+0.006 0+0.004 4)×50=0.7,
所以所求户数为0.7×100=70.
角度4 折线图的应用
2.机器人是一种能够半自主或全自主工作的智能机器.它可以辅助甚至替代人类完成某些工作,提高工作效率,服务人类生活,扩大或延伸人的活动及能力范畴.某公司为了研究某机器人的销售情况,统计了2020年2月至7月M,N两店每月该机器人的营业额(单位:万元),得到如图所示的折线图,则下列说法中错误的是( )
A.N店营业额的平均值是29
B.M店营业额的平均值在[34,35]内
C.N店营业额总体呈上升趋势
D.M店营业额的极差比N店营业额的极差大
D
角度5 总体百分位数的估计
3.对某种电子元件使用寿命跟踪调查,所得样本的频率分布直方图如图所示.由图可知,这一批电子元件中寿命的85%分位数为____ h.
答案:500
角度6 总体集中、离散趋势的估计
4.教育部、发展改革委、财政部、体育总局《关于进一步加强学校体育工作的若干意见》中指出:把提高学生体质健康水平作为落实教育规划纲要和办好人民满意教育的重要任务.某中学对2021年秋季入学的高一年级学生身高进行调查.采用样本量比例分配的分层随机抽样,如果不知道样本数据,只知道抽取了男生23人,其平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分别为160.6和38.62,由此估计高一年级学生身高的平均数为__________,总体方差为__________.
答案:165.2 51.486 2
1.众数、中位数、平均数与直方图的关系
(1)众数为频率分布直方图中最高矩形的底边中点的横坐标.
(2)中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.
(3)平均数等于频率分布直方图中每个小矩形的面积乘小矩形底边中点的横坐标之和.
2.方差的计算与含义
计算方差首先要计算平均数,再按照方差的计算公式进行计算,方差和标准差是描述一个样本和总体的波动大小的特征数,方差、标准差越大说明波动越大.
1.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2019年9月到2020年2月这半年中,某个关键词的搜索指数变化的走势图.
【巩固训练】
根据该走势图,下列结论正确的是( )
A.这半年中,网民对该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D.从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
解析:根据走势图可知,这半年中,网民对该关键词相关的信息关注度不呈周期性变化,A错;这半年中,网民对该关键词相关的信息关注度增减不确定,B错;从网民对该关键词的搜索指数来看,去年10月份的搜索指数的稳定性小于11月份的搜索指数的稳定性,所以去年10月份的方差大于11月份的方差,C错;从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值,D正确.
答案:D
2.数据组87,86,90,82,83,85,88,80,79,90的方差为__________,第80百分位数为__________.
答案:13.8 89
3.某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1∶2∶1,用分层随机抽样的方法从3个分厂生产的电子产品中共抽取100件进行使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的平均使用寿命分别为980 h,1 020 h,1 032 h,则抽取的100件产品的平均使用寿命为
A.1 013 h B.1 014 h C.1 016 h D.1 022 h
√
解析 方法一 由分层随机抽样的知识可知,从第一、二、三分厂抽取的电子产品数量分别为25件,50件,25件,
则抽取的100件产品的平均使用寿命为
方法二 因为第一、二、三分厂的产量之比为1∶2∶1,
所以可以根据各层抽取数量所占的比例计算抽取的100件产品的平均使
用寿命为
5.(2019·全国Ⅱ)某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y的分组 [-0.20,0) [0,0.20) [0.20,0.40) [0.40,0.60) [0.60,0.80]
企业数 2 24 53 14 7
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
解:根据产值增长率频数分布表得,所调查的100个企业中产值增长率不低于40%的企业频率为 =0.21.
用样本频率分布估计总体分布得这类企业中产值增长率不低于40%的企业比例为21%,产值负增长的企业比例为2%.
=0.029 6,
所以,这类企业产值增长率的平均数与标准差的估计值分别为0.30,0.17.
同课章节目录
