北师大版九年级数学下册 第二章 二次函数 复习 课件(共30张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 第二章 二次函数 复习 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 07:45:05 | ||
图片预览







文档简介
(共30张PPT)
二次函数复习
说一说:通过二次函数的学习,
你应该学什么?你学会了什么?
1、理解二次函数的概念;
2、会用描点法画出二次函数的图象;
3、会用配方法和公式确定抛物线的开口方向,
对称轴,顶点坐标;
4、会用待定系数法求二次函数的解析式;
5、能用二次函数的知识解决生活中的实际问题
及简单的综合运用。
我思考,我进步
想一想
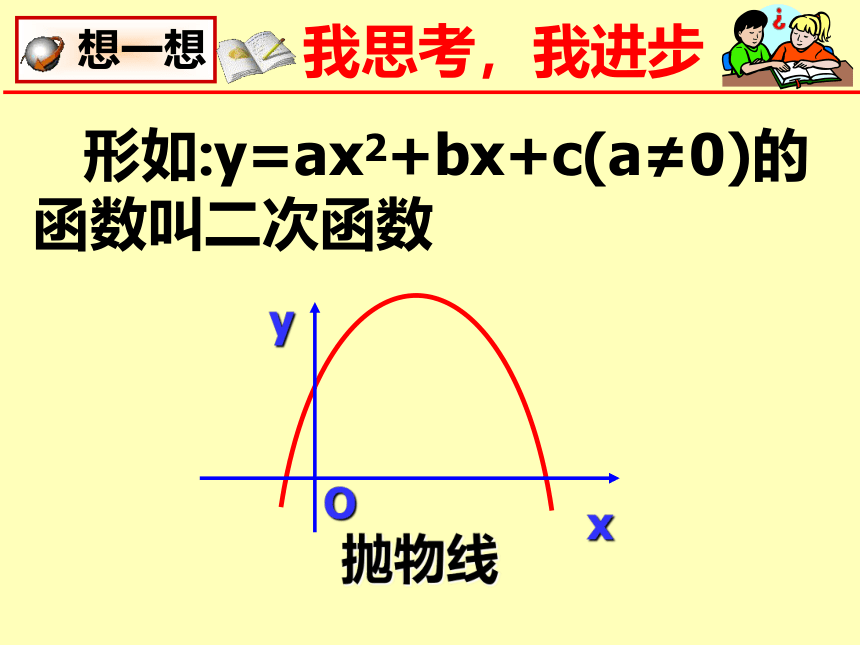
抛物线
形如:y=ax2+bx+c(a≠0)的函数叫二次函数
y
x
O
我思考,我进步
想一想
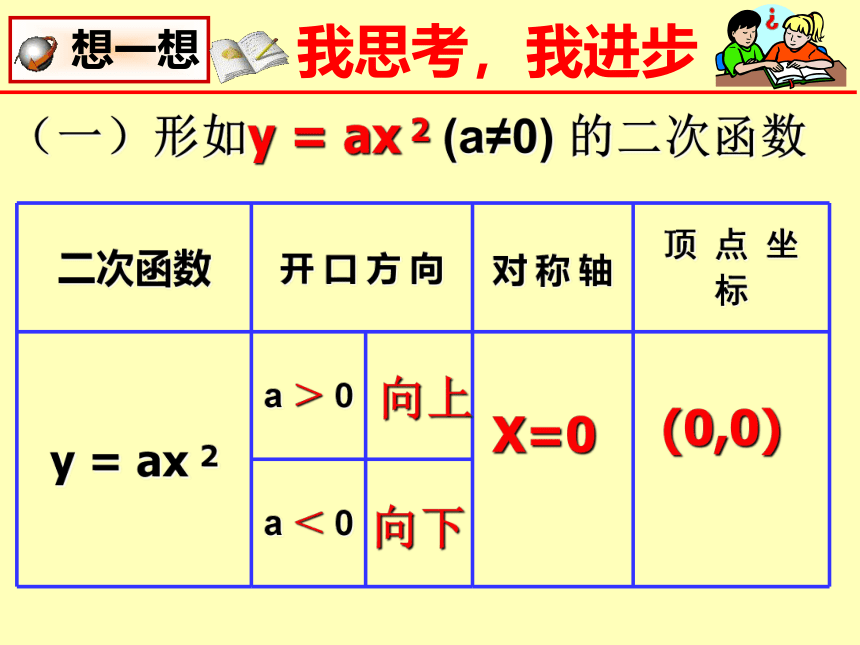
(一)形如y = ax 2 (a≠0) 的二次函数
二次函数 开 口 方 向 对 称 轴 顶 点 坐 标
y = ax 2 a > 0
a < 0
向上
向下
X=0
(0,0)
我思考,我进步
想一想
X
y
o
1
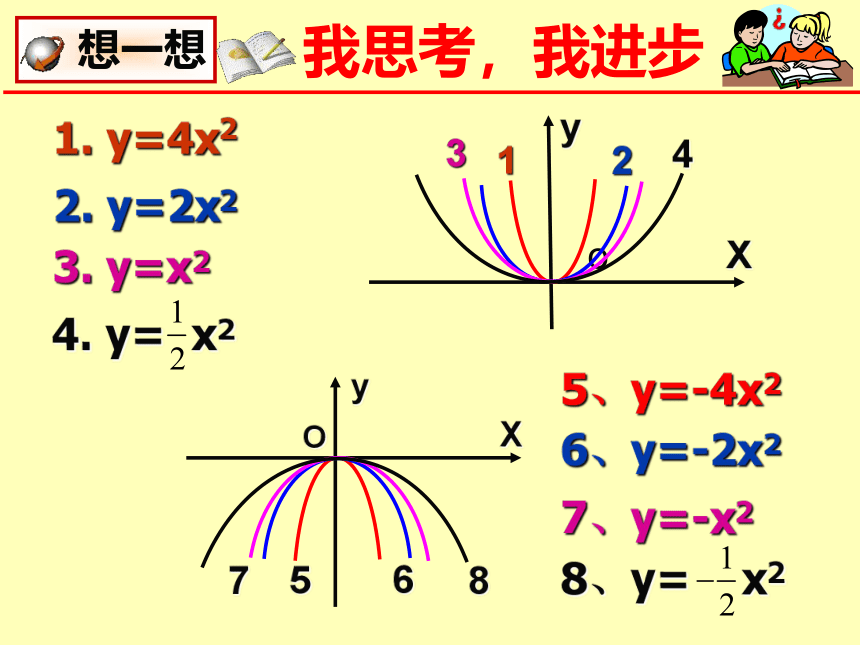
1. y=4x2
2
2. y=2x2
3
3. y=x2
4
X
y
O
5
6
7
8
5、y=-4x2
6、y=-2x2
7、y=-x2
我思考,我进步
想一想
4. y= x2
8、y= x2
(2)已知二次函数y = mx 2的图象如图,则m 0;若图象过 (2,- 4),则m= ;
o
.A
巩固练习1:
(1)抛物线y= x2的开口向 ,对称轴是 ,顶点坐标是 ,图象过第 象限 ;
上
Y轴
(0,0)
1、2
<
-1
业精于勤荒于嬉
小试牛刀
(3)已知y = - nx 2 (n>0) , 则图象 ( ) 过点A(-2,3)。 (填“可能”或“不可能”)
不可能
业精于勤荒于嬉
小试牛刀
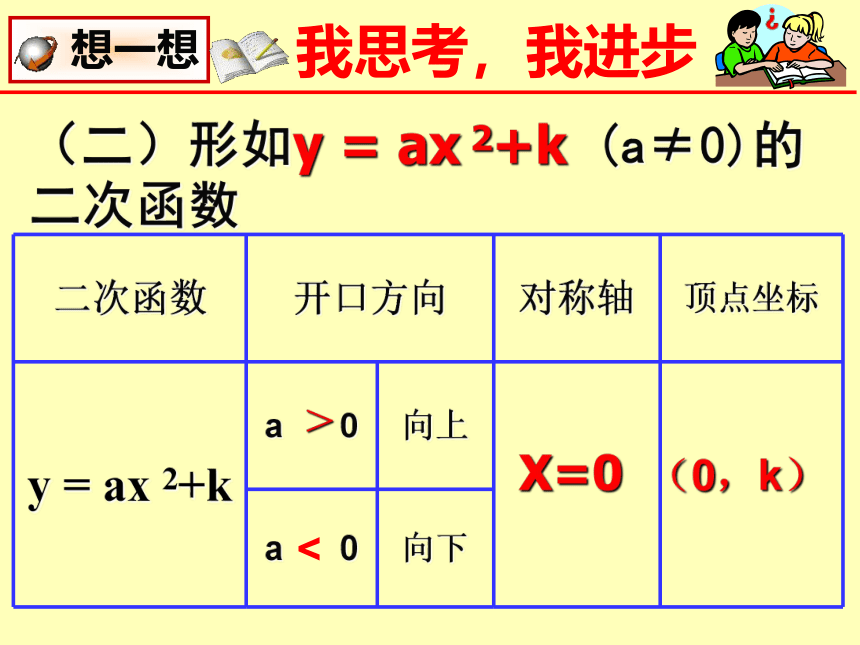
(二)形如y = ax 2+k (a≠0)的二次函数
二次函数 开口方向 对称轴 顶点坐标
y = ax 2+k a 0 向上
a 0 向下
>
<
X=0
(0,k)
我思考,我进步
想一想
巩固练习2:
(1)抛物线y = x 2+3的开口向 ,对称轴是 ,顶点坐标是 ,是由抛物线
y = x 2向 平移 个单位得到的;
上
X=0
(0,3)
上
3
业精于勤荒于嬉
小试牛刀
(2)已知(如图)抛物线y = ax 2+k的图象,则a 0,k 0;
若图象过A (0,-2) 和B (2,0) ,则a = ,k = ;
函数关系式是
y = 。
>
<
-2
X
Y
A
B
O
业精于勤荒于嬉
小试牛刀
x2-2
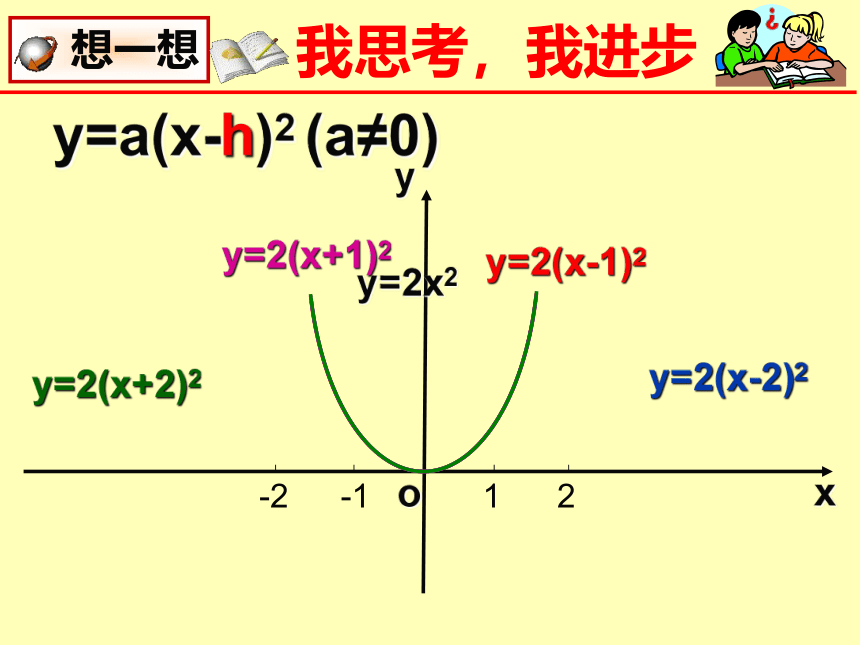
(三)形如y = a (x-h) 2( a≠0 )的二次函数
二次函数 开口方向 对称轴 顶点坐标
y = a(x-h) 2 a > 0
a <0
向上
向下
x=h
(h,0)
我思考,我进步
想一想
x
y
o
1
2
-1
-2
y=2x2
y=2(x-1)2
y=2(x-2)2
y=2(x+1)2
y=2(x+2)2
y=a(x-h)2 (a≠0)
我思考,我进步
想一想
练习巩固3:
y = - 2(x+3) 2的开口向 ,对称轴是 ,
顶点坐标是 ,
下
x=-3
(-3,0)
业精于勤荒于嬉
小试牛刀
(2)如图是y = a(x-h)2的图象,则a 0,h 0 ;
若图象过A (2,0) 和B (0,-4) 则a = , h = ;
函数关系式是y = 。
<
>
-1
2
-(X-2)2
O
A
B
X
y
业精于勤荒于嬉
小试牛刀
(四) 形如y = a (x-h) 2 +k (a ≠0) 的二次函数
二次函数 开口方向 对称轴 顶点坐标
y = a(x-h) 2+k 向上
向下
a > 0
a < 0
x=h
(h,k)
我思考,我进步
想一想
练习巩固4:
(1)抛物线 y = 2 (x - ) 2+1 的开口向 , 对称轴 , 顶点坐标是 ;
(2)若抛物线y = a (x+m) 2+n开口向下,顶点在第四象限,则a 0, m 0, n 0
上
<
<
<
业精于勤荒于嬉
小试牛刀
X=
( ,1)
x
y
o
1
2
-1
-2
1
2
y=2x2
y=2(x-1)2
y=2(x-1)2+2
Y=a(x-h)2+k
Y=2(x-1) +2的图象可看作是由y=2x 的图象经过怎样平移得到的
2
2
x
y
o
1
2
-1
1
2
y=2x2
y=2x2+2
y=2(x-1)2+2
y=a(x-h)2+k
-1
-2
-3
-4
0
1
2
3
4
1
2
3
4
5
6
-1
-2
观察y=x2与y=x2-6x+7的函数图象,说说y=x2-6x+7的图象
是怎样由y=x2的图象平移得到的?
y=x2-6x+7
=x2-6x+9-2
=(x-3)2-2
基础练习
1.由y=2x2的图象向左平移两个单位,再向下平 移三个单位,得到的图象的函数解析式为
________________________
2.由函数y= -3(x-1)2+2的图象向右平移4个单位,再向上平移3个单位,得到的图象的函数解析式为:
_____________________________
y=2(x+2)2-3
=2x2+8x+5
y= - 3(x-1-4)2+2+3
=-3x2+30x-70
业精于勤荒于嬉
小试牛刀
a决定了抛物线的____和___
对称轴由___决定;
c决定了图象与_____轴的交点位置;
开口方向
形状
a和b
y
当a的绝对值相等时,其形状完全相同,当a的绝对值越大,则开口越小,反之成立
我思考,我进步
想一想
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
我思考,我进步
想一想
3.说说下列二次函数的开口方向,对称轴,顶点坐标.
y= -2x2 - 4x - 6
y=x2 - 2x + 1
解:y=x2-2x+1
=(x-1)2
因为a=1>0,
所以开口向上
对称轴:直线x=1
顶点坐标:(1,0)
解:y= -2x2-4x-6
= -2(x2+2x+1+2)
= -2(x+1)2-4
因为a=-2<0,
所以开口向下
对称轴:直线x=-1
顶点坐标:(-1,-4)
业精于勤荒于嬉
小试牛刀
4.选择
抛物线y=x2-4x+3的对称轴是______.
A 直线x=1 B直线x= -1
C 直线x=2 D直线x= -2
(2)抛物线y=3x2-1的__________
A 开口向上,有最高点 B 开口向上,有最低点
C 开口向下,有最高点 D 开口向下,有最低点
c
B
业精于勤荒于嬉
小试牛刀
4.选择
(3)若y=ax2+bx+c(a 0)与x轴交于点A(2,0)、B(4,0),则对称轴是_______
A直线x=2 B直线x=4 C直线x=3 D直线x= -3
(4)若y=ax2+bx+c(a 0)与x轴交于点A(2,m), B(4,m),则对称轴是_______
A 直线x=3 B 直线x=4 C直线x= -3 D直线x=2
C
A
业精于勤荒于嬉
小试牛刀
探究练习:
1.若a>0,b>0,c>0,你能否画出y=ax2+bx+c的大致图象呢
0
0
0
要画出二次函数的大致图象,不但要知道a,b,c的符号,还必须明白b2-4ac的正负.
业精于勤荒于嬉
小试牛刀
2.已知y=ax2+bx+c的图象如图所示,
a___0, b_ _0, c___0, abc___0
b 2a, 2a-b___0, 2a+b___0
b2-4ac___0
a+b+c___0,
a-b+c___0
4a-2b+c___0
业精于勤荒于嬉
小试牛刀
<
<
>
>
=
=
<
>
<
>
>
0
-1
1
-2
0
0
A
B
A
B
对称是一种数学美,它展示出整体的和谐与平衡之美,抛物线是轴对称图形,解题中应积极捕捉,创造对称关系,以便从整体上把握问题,由抛物线捕捉对称信息的方式有:
1.从抛物线上两点的纵坐标相等获得对称信息;
2.从抛物线上两点之间的线段被抛物线的对称轴垂直平分获得对称信息.
2、已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________
3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________
1、已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2) (a≠0)
求抛物线解析式的三种方法
练习 根据下列条件,求二次函数的解析式。
(1)图象经过(0,0), (1,-2) , (2,3) 三点;
(2)图象的顶点(2,3), 且经过点(3,1) ;
(3)图象经过(0,0), (12,0) ,且最高点的纵坐标是3 。
二次函数复习
说一说:通过二次函数的学习,
你应该学什么?你学会了什么?
1、理解二次函数的概念;
2、会用描点法画出二次函数的图象;
3、会用配方法和公式确定抛物线的开口方向,
对称轴,顶点坐标;
4、会用待定系数法求二次函数的解析式;
5、能用二次函数的知识解决生活中的实际问题
及简单的综合运用。
我思考,我进步
想一想
抛物线
形如:y=ax2+bx+c(a≠0)的函数叫二次函数
y
x
O
我思考,我进步
想一想
(一)形如y = ax 2 (a≠0) 的二次函数
二次函数 开 口 方 向 对 称 轴 顶 点 坐 标
y = ax 2 a > 0
a < 0
向上
向下
X=0
(0,0)
我思考,我进步
想一想
X
y
o
1
1. y=4x2
2
2. y=2x2
3
3. y=x2
4
X
y
O
5
6
7
8
5、y=-4x2
6、y=-2x2
7、y=-x2
我思考,我进步
想一想
4. y= x2
8、y= x2
(2)已知二次函数y = mx 2的图象如图,则m 0;若图象过 (2,- 4),则m= ;
o
.A
巩固练习1:
(1)抛物线y= x2的开口向 ,对称轴是 ,顶点坐标是 ,图象过第 象限 ;
上
Y轴
(0,0)
1、2
<
-1
业精于勤荒于嬉
小试牛刀
(3)已知y = - nx 2 (n>0) , 则图象 ( ) 过点A(-2,3)。 (填“可能”或“不可能”)
不可能
业精于勤荒于嬉
小试牛刀
(二)形如y = ax 2+k (a≠0)的二次函数
二次函数 开口方向 对称轴 顶点坐标
y = ax 2+k a 0 向上
a 0 向下
>
<
X=0
(0,k)
我思考,我进步
想一想
巩固练习2:
(1)抛物线y = x 2+3的开口向 ,对称轴是 ,顶点坐标是 ,是由抛物线
y = x 2向 平移 个单位得到的;
上
X=0
(0,3)
上
3
业精于勤荒于嬉
小试牛刀
(2)已知(如图)抛物线y = ax 2+k的图象,则a 0,k 0;
若图象过A (0,-2) 和B (2,0) ,则a = ,k = ;
函数关系式是
y = 。
>
<
-2
X
Y
A
B
O
业精于勤荒于嬉
小试牛刀
x2-2
(三)形如y = a (x-h) 2( a≠0 )的二次函数
二次函数 开口方向 对称轴 顶点坐标
y = a(x-h) 2 a > 0
a <0
向上
向下
x=h
(h,0)
我思考,我进步
想一想
x
y
o
1
2
-1
-2
y=2x2
y=2(x-1)2
y=2(x-2)2
y=2(x+1)2
y=2(x+2)2
y=a(x-h)2 (a≠0)
我思考,我进步
想一想
练习巩固3:
y = - 2(x+3) 2的开口向 ,对称轴是 ,
顶点坐标是 ,
下
x=-3
(-3,0)
业精于勤荒于嬉
小试牛刀
(2)如图是y = a(x-h)2的图象,则a 0,h 0 ;
若图象过A (2,0) 和B (0,-4) 则a = , h = ;
函数关系式是y = 。
<
>
-1
2
-(X-2)2
O
A
B
X
y
业精于勤荒于嬉
小试牛刀
(四) 形如y = a (x-h) 2 +k (a ≠0) 的二次函数
二次函数 开口方向 对称轴 顶点坐标
y = a(x-h) 2+k 向上
向下
a > 0
a < 0
x=h
(h,k)
我思考,我进步
想一想
练习巩固4:
(1)抛物线 y = 2 (x - ) 2+1 的开口向 , 对称轴 , 顶点坐标是 ;
(2)若抛物线y = a (x+m) 2+n开口向下,顶点在第四象限,则a 0, m 0, n 0
上
<
<
<
业精于勤荒于嬉
小试牛刀
X=
( ,1)
x
y
o
1
2
-1
-2
1
2
y=2x2
y=2(x-1)2
y=2(x-1)2+2
Y=a(x-h)2+k
Y=2(x-1) +2的图象可看作是由y=2x 的图象经过怎样平移得到的
2
2
x
y
o
1
2
-1
1
2
y=2x2
y=2x2+2
y=2(x-1)2+2
y=a(x-h)2+k
-1
-2
-3
-4
0
1
2
3
4
1
2
3
4
5
6
-1
-2
观察y=x2与y=x2-6x+7的函数图象,说说y=x2-6x+7的图象
是怎样由y=x2的图象平移得到的?
y=x2-6x+7
=x2-6x+9-2
=(x-3)2-2
基础练习
1.由y=2x2的图象向左平移两个单位,再向下平 移三个单位,得到的图象的函数解析式为
________________________
2.由函数y= -3(x-1)2+2的图象向右平移4个单位,再向上平移3个单位,得到的图象的函数解析式为:
_____________________________
y=2(x+2)2-3
=2x2+8x+5
y= - 3(x-1-4)2+2+3
=-3x2+30x-70
业精于勤荒于嬉
小试牛刀
a决定了抛物线的____和___
对称轴由___决定;
c决定了图象与_____轴的交点位置;
开口方向
形状
a和b
y
当a的绝对值相等时,其形状完全相同,当a的绝对值越大,则开口越小,反之成立
我思考,我进步
想一想
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
我思考,我进步
想一想
3.说说下列二次函数的开口方向,对称轴,顶点坐标.
y= -2x2 - 4x - 6
y=x2 - 2x + 1
解:y=x2-2x+1
=(x-1)2
因为a=1>0,
所以开口向上
对称轴:直线x=1
顶点坐标:(1,0)
解:y= -2x2-4x-6
= -2(x2+2x+1+2)
= -2(x+1)2-4
因为a=-2<0,
所以开口向下
对称轴:直线x=-1
顶点坐标:(-1,-4)
业精于勤荒于嬉
小试牛刀
4.选择
抛物线y=x2-4x+3的对称轴是______.
A 直线x=1 B直线x= -1
C 直线x=2 D直线x= -2
(2)抛物线y=3x2-1的__________
A 开口向上,有最高点 B 开口向上,有最低点
C 开口向下,有最高点 D 开口向下,有最低点
c
B
业精于勤荒于嬉
小试牛刀
4.选择
(3)若y=ax2+bx+c(a 0)与x轴交于点A(2,0)、B(4,0),则对称轴是_______
A直线x=2 B直线x=4 C直线x=3 D直线x= -3
(4)若y=ax2+bx+c(a 0)与x轴交于点A(2,m), B(4,m),则对称轴是_______
A 直线x=3 B 直线x=4 C直线x= -3 D直线x=2
C
A
业精于勤荒于嬉
小试牛刀
探究练习:
1.若a>0,b>0,c>0,你能否画出y=ax2+bx+c的大致图象呢
0
0
0
要画出二次函数的大致图象,不但要知道a,b,c的符号,还必须明白b2-4ac的正负.
业精于勤荒于嬉
小试牛刀
2.已知y=ax2+bx+c的图象如图所示,
a___0, b_ _0, c___0, abc___0
b 2a, 2a-b___0, 2a+b___0
b2-4ac___0
a+b+c___0,
a-b+c___0
4a-2b+c___0
业精于勤荒于嬉
小试牛刀
<
<
>
>
=
=
<
>
<
>
>
0
-1
1
-2
0
0
A
B
A
B
对称是一种数学美,它展示出整体的和谐与平衡之美,抛物线是轴对称图形,解题中应积极捕捉,创造对称关系,以便从整体上把握问题,由抛物线捕捉对称信息的方式有:
1.从抛物线上两点的纵坐标相等获得对称信息;
2.从抛物线上两点之间的线段被抛物线的对称轴垂直平分获得对称信息.
2、已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________
3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________
1、已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2) (a≠0)
求抛物线解析式的三种方法
练习 根据下列条件,求二次函数的解析式。
(1)图象经过(0,0), (1,-2) , (2,3) 三点;
(2)图象的顶点(2,3), 且经过点(3,1) ;
(3)图象经过(0,0), (12,0) ,且最高点的纵坐标是3 。
