数列中的不等式问题 学案(Word版含解析)
文档属性
| 名称 | 数列中的不等式问题 学案(Word版含解析) |  | |
| 格式 | DOCX | ||
| 文件大小 | 120.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-01 20:07:02 | ||
图片预览

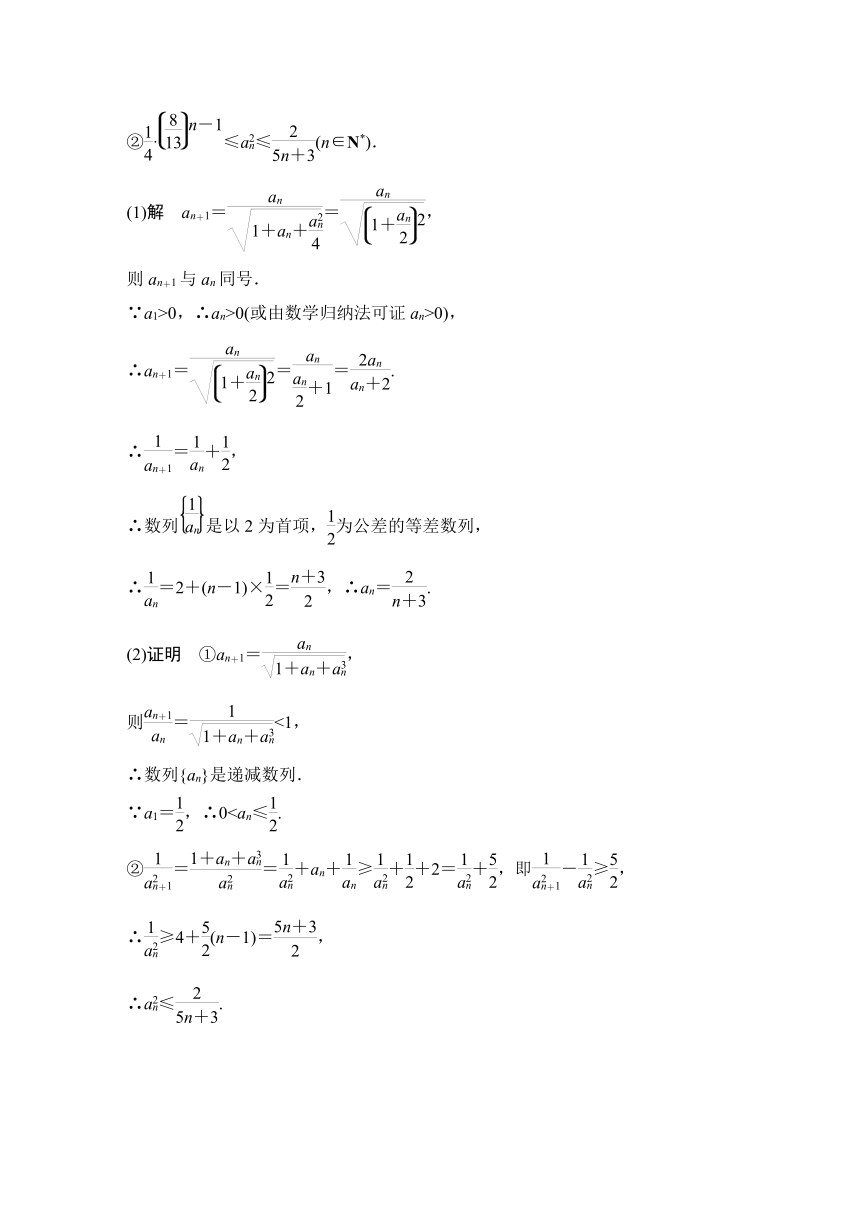



文档简介
本资料分享自新人教版高中数学资源大全QQ群323031380 期待你的加入与分享
数列中的不等式问题
1.数列中的不等式问题在我省高考试卷中有加强趋势,主要有以下几种题型:
(1)数列不等式的证明;
(2)由数列不等式恒成立求参数;
(3)由数列不等式求n的最值.
2.解决数列不等式问题的常见放缩技巧
(1)对的放缩,根据不同的要求,大致有三种情况:
<=-(n≥2);
<=(n≥2);
<=2(n≥1).
(2)对的放缩,根据不同的要求,大致有两种情况:
>=-(n≥1);
<=-(n≥1).
题型一 关于数列项的不等式证明
【例1】 (2021·杭州模拟)已知数列{an},{bn}满足a1=,an+1=(n∈N*).
(1)若bn=,求证数列是等差数列,并求数列{an}的通项公式;
(2)若bn=a,求证:①0②·≤a≤(n∈N*).
(1)解 an+1==,
则an+1与an同号.
∵a1>0,∴an>0(或由数学归纳法可证an>0),
∴an+1===.
∴=+,
∴数列是以2为首项,为公差的等差数列,
∴=2+(n-1)×=,∴an=.
(2)证明 ①an+1=,
则=<1,
∴数列{an}是递减数列.
∵a1=,∴0②==+an+≥++2=+,即-≥,
∴≥4+(n-1)=,
∴a≤.
∵=≥=,
∴a≥·.
综上所述,·≤a≤(n∈N*).
感悟升华 常用方法
(1)利用数列的单调性、有界性放缩;
(2)结合“累加”“累乘”“迭代”放缩;
(3)结合有界性,利用不等式性质或函数求出最值或范围.
【训练1】 (2021·镇海中学模拟)已知数列{an}满足a1=1,an-1=an(n≥2,n∈N*).
(1)求an;
(2)若数列{bn}满足b1=,bn+1=bn+(n∈N*),求证:bn(1)解 由an-1=an(n≥2,n∈N*)得=(n≥2,n∈N*),
则累乘得an=n(n≥2).
又因为a1=1满足上式,所以an=n.
(2)证明 由(1)得bn+1-bn==>0,
所以bn+1>bn,则bn+1-bn=<,
则-=<<=-,
累加得-<1-.
又b2=b1+=,
所以>+>1,
则bn+1<1,所以bn当n=1时,不等式也成立,
所以对任意n∈N*,都有bn题型二 数列和不等式的证明
角度1 先放缩再求和
【例2-1】 (2021·杭州质检)设公差不为0的等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,若a2是a1与a4的等比中项,a6=12,a1b1=a2b2=1.
(1)求an,Sn与Tn;
(2)若cn=,求证:c1+c2+…+cn<.
(1)解 设等差数列{an}的公差为d,由题意得
a=a1·a4,
即d2=a1d.
因为d≠0,故d=a1.
由a6=12得a1=2,d=2,故an=2n,Sn=n(n+1).
由a1·b1=a2·b2=1得b1=,b2=,所以等比数列的公比q==,
所以Tn=1-.
(2)证明 因为cn==,0<1-<1恒成立,
所以ck<<=k+(k∈N*),
所以c1+c2+…+cn<=.
故c1+c2+…+cn<.
角度2 先求和再放缩
【例2-2】 (2021·台州期末)设数列{an}的前n项和为Sn,对于任意的正整数n,都有Sn=n2.递增的等比数列{bn}满足:b1=1,且b1,b2,b3-4成等差数列.
(1)求数列{an},{bn}的通项公式;
(2)求证:++…+<3.
(1)解 因为Sn=n2,
所以当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
当n=1时,a1=S1=1,适合上式,
所以数列{an}的通项公式为an=2n-1.
设等比数列{bn}的公比为q(其中q>0),因为b1=1,
故由2b2=b1+b3-4,b1=1,可得q2-2q-3=0,
解得q=3或-1(舍去),
所以数列{bn}的通项公式为bn=3n-1.
(2)证明 法一 由(1)可得=,因为n≥2时,3n-1=(1+2)n-1>-1+1+2C+22C>2n+1,
根据“若a>b>0,m>0,则<”,
可得=<(n≥2),
所以++…+≤++…+.
令Tn=++…+,
Tn=++…++,
两式相减可得Tn=+++…+-
=+-=--,
所以Tn=-,所以Tn<,所以++…+<+=<3.
法二 令cn==,下一步用分析法证明<,
要证<,即证<,
即证(4n+6)(3n-1)<(2n+1)(3n+1-1),
即证-2n-5<(2n-3)3n,
当n∈N*时,显然成立,所以<,
所以c1+c2+…+cn=++…+
≤+×+…+×
=×=3<3.
感悟升华 (1)易求和时,一般先求和再放缩或求其最值;
(2)不易求和时,应先放缩再求和,常用方法有:
①对(1+x)n形式注意运用二项式定理;
②分式放缩,注意用分式不等式性质;
③“和”“积”转换注意应用基本不等式;
④有时利用函数不等式ex≥x+1,ln x≤x-1(x>0)放缩;
⑤注意添减项(多为常数)放缩.
【训练2】 (1)(角度1)(2021·镇海中学检测)已知正数数列{an}的前n项和为Sn,且满足2S-(n2+n)Sn-(n2+n+2)=0.
①求数列{an}的通项公式;
②设数列bn=,证明:b1+b2+…+bn≤2-1.
(2)(角度2)已知等差数列{an}的前n项和为Sn,且a2+2a4=a9,S6=36.
①求an,Sn;
②若数列{bn}满足b1=1,bn+1bn=,求证:++…+≥2-1(n∈N*).
(1)①解 由2S-(n2+n)Sn-(n2+n+2)=0得
(Sn+1)[2Sn-(n2+n+2)]=0,
结合正数数列得Sn=,
所以an=
②证明 由①知bn=
当n≥2时,bn==<=<=2(-),
所以b1+b2+…+bn≤1+2(-+-+…+-)=2-1.
(2)①解 设等差数列{an}的公差为d,
则由条件得
解得a1=1,d=2,
所以an=1+(n-1)×2=2n-1,
所以Sn==n2.
②证明 由①知,bn+1bn=n,
当n=1时,解得b2=1.
因为当n≥2时,bnbn-1=n-1,
所以bn+1bn-bnbn-1=1,bn(bn+1-bn-1)=1,
即=bn+1-bn-1,
当n≥2时,+++…+=+(b3-b1)+(b4-b2)+(b5-b3)+…+(bn+1-bn-1)=-b1-b2+bn+bn+1≥-1+2=2-1.
当n=1时,=1≥2-1,不等式也成立.
综上,不等式++…+≥2-1对任意n∈N*都成立.
题型三 数列不等式恒成立求参数
【例3】 (2021·杭州质检)已知数列{an}的各项均为正数,a1=,bn=,{bn}是等差数列,其前n项和为Sn,b2·S6=81.
(1)求数列{an}的通项公式;
(2)设cn=(1-a1)(1-a2)…(1-an),Tn=+++…+,若对任意的正整数n,都有4aTn解 (1)设数列{bn}的公差为d,由b1==2,
b2·S6=81,得(2+d)(12+15d)=81,
即5d2+14d-19=0,解得d=1或d=-.
因为数列{an}的各项均为正数,b1=2,
所以d≥0,所以d=1,
所以bn=n+1,所以an=.
(2)由题意得cn=…=·…·=,
因为=·=
=2,
所以Tn=2
=,
所以不等式4aTn即8a<=1++恒成立,
而函数g(n)=1++在定义域上单调递减,且g(n)>1,
所以8a≤1,即a≤.
故a的取值范围为.
感悟升华 (1)能分离参数时,常分离参数,化为函数求最值、值域问题;
(2)不能分离参数时,常分类讨论.
【训练3】 (2021·义乌联考)已知等比数列{an},满足a1=3,a3=a1a2,数列{bn}满足b1=1,对一切正整数n均有bn+1=bn+2n+1.
(1)求数列{an}和{bn}的通项公式;
(2)记Sk=+++…+,Tn=+++…+,若存在实数c和正整数k,使得不等式Tn<(c-1)·Sk对任意正整数n都成立,求实数c的取值范围.
解 (1)设等比数列{an}的公比为q,
由题可知a3=a1a2.
∴a1q2=aq,
即3q2=9q,解得q=3,
∴an=3n.
因为bn+1=bn+2n+1,则bn+1-bn=2n+1,
累加可得bn-b1=
=(n+1)(n-1),
所以bn=(n+1)(n-1)+1=n2.
(2)∵=,∴Sk=+++…+,
Sk=+++…++,
两式相减得Sk=++++…+-=-=1--,
∴Sk=-<.
∵===,
∴Tn=+++…+
==-<.
若存在实数c和正整数k使得不等式Tn<(c-1)·Sk对任意正整数n都成立,
当c>1时,<(c-1)·,c>;
当c≤1时,<(c-1)·S1=(c-1)·,此时无解.
综上,c>.
题型四 根据所给不等式求n的最值(范围)
【例4】 (2021·湖州期末)已知Sn是数列{an}的前n项和,a1=1且nSn+1=(n+2)Sn,n∈N*.
(1)求数列{an}的通项公式;
(2)设bn=(-1)n(n∈N*),数列{bn}的前n项和为Pn,若|Pn+1|<,求正整数n的最小值.
解 (1)由nSn+1=(n+2)Sn得=,
所以当n≥2时,Sn=···…····S1=×××…××××1=.
又当n=1时,S1=a1=1也成立,所以Sn=,
所以当n≥2时,an=Sn-Sn-1=-=n.
又a1=1也成立,所以an=n.
(2)由(1)知bn=(-1)n
=(-1)n,
所以Pn=-1-++--+…+(-1)n·+(-1)n=-1+
(-1)n,
所以|Pn+1|=< n>.
因为n为正整数,所以n的最小值是1 010.
感悟升华 此类问题多归结为解关于n的不等式解决.
【训练4】 (2021·名校仿真训练卷五)数列{an}中,a1=2,(n+1)(an+1-an)=2(an+n+1).
(1)求a2,a3的值;
(2)已知数列{an}的通项公式是an=n+1,an=n2+1,an=n2+n中的一个,设数列的前n项和为Sn,数列{an+1-an}的前n项和为Tn,若>360,求n的取值范围.
解 (1)∵(n+1)(an+1-an)=2(an+n+1),
∴an+1=an+2,
∴a2=a1+2=6,a3=a2+2=12.
(2)∵数列{an}的通项公式是an=n+1,an=n2+1,an=n2+n中的一个,且a2=6,
∴数列{an}的通项公式是an=n2+n=n(n+1).
由an=n(n+1)可得==-.
∴++…+=++…+=1-,
∴Sn=1-.
∵(a2-a1)+(a3-a2)+…+(an+1-an)=an+1-a1,
an=n(n+1),
∴(a2-a1)+(a3-a2)+…+(an+1-an)=n2+3n,
即Tn=n2+3n.
由>360得n2+4n-357>0,解得n>17或n<-21.
∵n是正整数,
∴所求n的取值范围为(17,+∞),且n是正整数.
1.设正项数列{an}满足a1=1,an+1=an+(n∈N*).
(1)求证:2≤a-a≤3;
(2)求证:≤≤.
证明 (1)因为a1=1及an+1=an+(n≥1),所以an≥1,所以0<≤1.因为a==a++2,
所以a-a=+2∈(2,3],即2≤a-a≤3.
(2)由(1)得2n所以2n+1即2n-1所以2n-1所以=1+∈.
2.(2021·衢州、湖州、丽水质检)已知数列{an}的前n项和Sn=,且an>0(n∈N*).
(1)写出a1,a2,a3的值,并求出数列{an}的通项公式;
(2)设bn=,Tn为数列{bn}的前n项和,求证:(1)解 当n=1时,a1=S1=.
又因为an>0,所以a1=2,a1+a2=S2=,
解得a2=4,同理,a3=6.
当n≥2时,an=Sn-Sn-1=-,
即(an+an-1)(an-an-1-2)=0.
因为an>0,所以an-an-1-2=0,即an-an-1=2,
所以数列{an}是首项为2,公差为2的等差数列,
故an=2n.
(2)证明 由(1)可得Sn=n(n+1),bn=,
所以bn>n,Tn>.
又bn=<=n+,
所以Tn<+=.
综上,3.(2021·浙江“超级全能生”联考)已知数列{an}满足a1=1,an=1+an-1(n>1),数列{bn}满足b1=1,1+a1b1+a2b2+…+an-1bn-1=an(n>1).
(1)求数列{an},{bn}的通项公式;
(2)若数列{cn}满足ancn=bn+2,求证:c1+c2+…+cn<.
(1)解 ∵a1=1,an=1+an-1,
∴an-an-1=1(n>1),
∴数列{an}是以1为首项,1为公差的等差数列,
∴an=n.
∵1+a1b1+a2b2+…+an-1bn-1=an,①
∴1+a1b1+a2b2+…+anbn=an+1,②
由②-①得anbn=an+1-an=1,
又∵an=n,∴bn=.
(2)证明 ∵ancn=bn+2,an=n,bn=,
∴cn=·=,
∴c1+c2+…+cn=
=
=-<.
4.(2021·嘉兴二测)已知数列{an}的前n项和为Sn,且Sn=.公比大于0的等比数列{bn}的首项b1=1,且b2+b3=20.
(1)求数列{an}和{bn}的通项公式;
(2)若cn=,求证:c1+c2+c3+…+cn<(n∈N*).
(1)解 当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=-=n.
当n=1时也满足上式,所以an=n.
设等比数列{bn}的公比为q>0,
则b2+b3=b1q+b1q2=q+q2=20,
解得q=4或q=-5(舍去),所以bn=4n-1.
(2)证明 由(1)知cn=,===,c1=c2=1,c3=.
当n≥2时,≤,
所以c1+c2+c3+c4+…+cn≤1+1+++…+=1+=1+<1+<.
5.已知等差数列{an}的公差d≠0,a1=25,且a1,a11,a13成等比数列.
(1)求使不等式an≥0成立的最大自然数n;
(2)记数列的前n项和为Tn,求证:-≤Tn≤.
(1)解 由题意可知a=a1·a13,
即(a1+10d)2=a1·(a1+12d),
∴d(2a1+25d)=0.
又a1=25,d≠0,
∴d=-2,∴an=-2n+27,
∴-2n+27≥0,∴n≤13.5,
故满足题意的最大自然数为n=13.
(2)证明 =
=-,
∴Tn=+++…+
=-+
=-
=-+.
从而当n≤12时,Tn=-+单调递增,且Tn>0;
当n≥13时,Tn=-+单调递增,且Tn<0,
∴T13≤Tn≤T12,由T12=,T13=-,
∴-≤Tn≤.
6.(2021·金华十校期末调研测试)已知数列{an}的前n项和为Sn,Sn是-3和3an的等差中项.
(1)求数列{an}的通项公式;
(2)若··…·≥λ对任意的正整数n恒成立,求实数λ的取值范围.
解 (1)由题意得2Sn=-3+3an,
则当n≥2时,2Sn-1=-3+3an-1,
∴当n≥2时,an=3an-1.
又由2S1=-3+3a1得a1=3,
∴数列{an}是以3为首项,3为公比的等比数列,
∴an=3n.
(2)由题意知2Sn=-3+3an,得=,
得··…·=··…·,
∴λ≤.
设bn=.
∵an=3n,∴bn>0,
∴=>1,
∴{bn}是递增数列,最小项是b1==,
∴λ≤,即实数λ的取值范围为 .
7.(2021·绍兴上虞区期末调测)在数列{an}中,已知a1=1,an+1=an+2n-1.
(1)求数列{an}的通项公式;
(2)记bn=an+(1-λ)n,且数列{bn}的前n项和为Sn,若S2为数列{Sn}中的最小项,求λ的取值范围.
解 (1)∵a2=a1+2-1,
a3=a2+22-1,
…
an-1=an-2+2n-2-1,
an=an-1+2n-1-1,
累加可得an-a1=2n-2-(n-1)(n≥2),
∴an=2n-n,
当n=1时,a1=2-1=1,则an=2n-n.
(2)由(1)得bn=an+(1-λ)n=2n-λn,
∴Sn=2n+1-2-λ≥S2=6-3λ,
即2n+1-8≥λ.
当n=1时,得-4≥-2λ,∴λ≥2;
当n=2时,λ∈R;
当n≥3时,得-3>0,∴λ≤.
令f(n)=,
则f(n+1)-f(n)=-=,
当n≥4时,n2-n-8>0,∴f(n+1)>f(n),
又可验证当n=3时,f(4)-f(3)>0也成立,
∴当n≥3时,数列{f(n)}为递增数列,
∴f(n)min=f(3)=,即λ≤.
综上所述,λ的取值范围为.
8.(2021·宁波期末)已知等差数列{an}满足a2=2a1,a4+a5=9,Sn为等比数列{bn}的前n项和,2Sn+1=Sn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn=证明:c1+c2+c3+…+cn<.
(1)解 由题意得解得
∴an=n,即数列{an}的通项公式为an=n.
由2Sn+1=Sn+2,得
两式相减整理得:2b3=b2,
∴q=,b1=1,
∴bn=,即数列{bn}的通项公式为bn=.
(2)证明 (应用放缩和错位相减法求和证明不等式)
令Cn=c1+c2+c3+…+cn,Ak=c1+c3+…+c2k-1,
Bk=c2+c4+…+c2k,
则Ak=,
利用错位相减法可求得Ak=-<.
又∵(2k)2>(2k-1)(2k+1),
∴Bk=++…+
<<=.
∴Bk=++…+<,
当n为偶数时,
Cn=A+B<-+<;
当n为奇数时,
Cn=A+B<-+<.
综上,Cn<,即c1+c2+c3+…+cn<.
本资料分享自新人教版高中数学资源大全QQ群483122854 期待你的加入与分享
数列中的不等式问题
1.数列中的不等式问题在我省高考试卷中有加强趋势,主要有以下几种题型:
(1)数列不等式的证明;
(2)由数列不等式恒成立求参数;
(3)由数列不等式求n的最值.
2.解决数列不等式问题的常见放缩技巧
(1)对的放缩,根据不同的要求,大致有三种情况:
<=-(n≥2);
<=(n≥2);
<=2(n≥1).
(2)对的放缩,根据不同的要求,大致有两种情况:
>=-(n≥1);
<=-(n≥1).
题型一 关于数列项的不等式证明
【例1】 (2021·杭州模拟)已知数列{an},{bn}满足a1=,an+1=(n∈N*).
(1)若bn=,求证数列是等差数列,并求数列{an}的通项公式;
(2)若bn=a,求证:①0
(1)解 an+1==,
则an+1与an同号.
∵a1>0,∴an>0(或由数学归纳法可证an>0),
∴an+1===.
∴=+,
∴数列是以2为首项,为公差的等差数列,
∴=2+(n-1)×=,∴an=.
(2)证明 ①an+1=,
则=<1,
∴数列{an}是递减数列.
∵a1=,∴0
∴≥4+(n-1)=,
∴a≤.
∵=≥=,
∴a≥·.
综上所述,·≤a≤(n∈N*).
感悟升华 常用方法
(1)利用数列的单调性、有界性放缩;
(2)结合“累加”“累乘”“迭代”放缩;
(3)结合有界性,利用不等式性质或函数求出最值或范围.
【训练1】 (2021·镇海中学模拟)已知数列{an}满足a1=1,an-1=an(n≥2,n∈N*).
(1)求an;
(2)若数列{bn}满足b1=,bn+1=bn+(n∈N*),求证:bn
则累乘得an=n(n≥2).
又因为a1=1满足上式,所以an=n.
(2)证明 由(1)得bn+1-bn==>0,
所以bn+1>bn,则bn+1-bn=<,
则-=<<=-,
累加得-<1-.
又b2=b1+=,
所以>+>1,
则bn+1<1,所以bn
所以对任意n∈N*,都有bn
角度1 先放缩再求和
【例2-1】 (2021·杭州质检)设公差不为0的等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,若a2是a1与a4的等比中项,a6=12,a1b1=a2b2=1.
(1)求an,Sn与Tn;
(2)若cn=,求证:c1+c2+…+cn<.
(1)解 设等差数列{an}的公差为d,由题意得
a=a1·a4,
即d2=a1d.
因为d≠0,故d=a1.
由a6=12得a1=2,d=2,故an=2n,Sn=n(n+1).
由a1·b1=a2·b2=1得b1=,b2=,所以等比数列的公比q==,
所以Tn=1-.
(2)证明 因为cn==,0<1-<1恒成立,
所以ck<<=k+(k∈N*),
所以c1+c2+…+cn<=.
故c1+c2+…+cn<.
角度2 先求和再放缩
【例2-2】 (2021·台州期末)设数列{an}的前n项和为Sn,对于任意的正整数n,都有Sn=n2.递增的等比数列{bn}满足:b1=1,且b1,b2,b3-4成等差数列.
(1)求数列{an},{bn}的通项公式;
(2)求证:++…+<3.
(1)解 因为Sn=n2,
所以当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
当n=1时,a1=S1=1,适合上式,
所以数列{an}的通项公式为an=2n-1.
设等比数列{bn}的公比为q(其中q>0),因为b1=1,
故由2b2=b1+b3-4,b1=1,可得q2-2q-3=0,
解得q=3或-1(舍去),
所以数列{bn}的通项公式为bn=3n-1.
(2)证明 法一 由(1)可得=,因为n≥2时,3n-1=(1+2)n-1>-1+1+2C+22C>2n+1,
根据“若a>b>0,m>0,则<”,
可得=<(n≥2),
所以++…+≤++…+.
令Tn=++…+,
Tn=++…++,
两式相减可得Tn=+++…+-
=+-=--,
所以Tn=-,所以Tn<,所以++…+<+=<3.
法二 令cn==,下一步用分析法证明<,
要证<,即证<,
即证(4n+6)(3n-1)<(2n+1)(3n+1-1),
即证-2n-5<(2n-3)3n,
当n∈N*时,显然成立,所以<,
所以c1+c2+…+cn=++…+
≤+×+…+×
=×=3<3.
感悟升华 (1)易求和时,一般先求和再放缩或求其最值;
(2)不易求和时,应先放缩再求和,常用方法有:
①对(1+x)n形式注意运用二项式定理;
②分式放缩,注意用分式不等式性质;
③“和”“积”转换注意应用基本不等式;
④有时利用函数不等式ex≥x+1,ln x≤x-1(x>0)放缩;
⑤注意添减项(多为常数)放缩.
【训练2】 (1)(角度1)(2021·镇海中学检测)已知正数数列{an}的前n项和为Sn,且满足2S-(n2+n)Sn-(n2+n+2)=0.
①求数列{an}的通项公式;
②设数列bn=,证明:b1+b2+…+bn≤2-1.
(2)(角度2)已知等差数列{an}的前n项和为Sn,且a2+2a4=a9,S6=36.
①求an,Sn;
②若数列{bn}满足b1=1,bn+1bn=,求证:++…+≥2-1(n∈N*).
(1)①解 由2S-(n2+n)Sn-(n2+n+2)=0得
(Sn+1)[2Sn-(n2+n+2)]=0,
结合正数数列得Sn=,
所以an=
②证明 由①知bn=
当n≥2时,bn==<=<=2(-),
所以b1+b2+…+bn≤1+2(-+-+…+-)=2-1.
(2)①解 设等差数列{an}的公差为d,
则由条件得
解得a1=1,d=2,
所以an=1+(n-1)×2=2n-1,
所以Sn==n2.
②证明 由①知,bn+1bn=n,
当n=1时,解得b2=1.
因为当n≥2时,bnbn-1=n-1,
所以bn+1bn-bnbn-1=1,bn(bn+1-bn-1)=1,
即=bn+1-bn-1,
当n≥2时,+++…+=+(b3-b1)+(b4-b2)+(b5-b3)+…+(bn+1-bn-1)=-b1-b2+bn+bn+1≥-1+2=2-1.
当n=1时,=1≥2-1,不等式也成立.
综上,不等式++…+≥2-1对任意n∈N*都成立.
题型三 数列不等式恒成立求参数
【例3】 (2021·杭州质检)已知数列{an}的各项均为正数,a1=,bn=,{bn}是等差数列,其前n项和为Sn,b2·S6=81.
(1)求数列{an}的通项公式;
(2)设cn=(1-a1)(1-a2)…(1-an),Tn=+++…+,若对任意的正整数n,都有4aTn
b2·S6=81,得(2+d)(12+15d)=81,
即5d2+14d-19=0,解得d=1或d=-.
因为数列{an}的各项均为正数,b1=2,
所以d≥0,所以d=1,
所以bn=n+1,所以an=.
(2)由题意得cn=…=·…·=,
因为=·=
=2,
所以Tn=2
=,
所以不等式4aTn
而函数g(n)=1++在定义域上单调递减,且g(n)>1,
所以8a≤1,即a≤.
故a的取值范围为.
感悟升华 (1)能分离参数时,常分离参数,化为函数求最值、值域问题;
(2)不能分离参数时,常分类讨论.
【训练3】 (2021·义乌联考)已知等比数列{an},满足a1=3,a3=a1a2,数列{bn}满足b1=1,对一切正整数n均有bn+1=bn+2n+1.
(1)求数列{an}和{bn}的通项公式;
(2)记Sk=+++…+,Tn=+++…+,若存在实数c和正整数k,使得不等式Tn<(c-1)·Sk对任意正整数n都成立,求实数c的取值范围.
解 (1)设等比数列{an}的公比为q,
由题可知a3=a1a2.
∴a1q2=aq,
即3q2=9q,解得q=3,
∴an=3n.
因为bn+1=bn+2n+1,则bn+1-bn=2n+1,
累加可得bn-b1=
=(n+1)(n-1),
所以bn=(n+1)(n-1)+1=n2.
(2)∵=,∴Sk=+++…+,
Sk=+++…++,
两式相减得Sk=++++…+-=-=1--,
∴Sk=-<.
∵===,
∴Tn=+++…+
==-<.
若存在实数c和正整数k使得不等式Tn<(c-1)·Sk对任意正整数n都成立,
当c>1时,<(c-1)·,c>;
当c≤1时,<(c-1)·S1=(c-1)·,此时无解.
综上,c>.
题型四 根据所给不等式求n的最值(范围)
【例4】 (2021·湖州期末)已知Sn是数列{an}的前n项和,a1=1且nSn+1=(n+2)Sn,n∈N*.
(1)求数列{an}的通项公式;
(2)设bn=(-1)n(n∈N*),数列{bn}的前n项和为Pn,若|Pn+1|<,求正整数n的最小值.
解 (1)由nSn+1=(n+2)Sn得=,
所以当n≥2时,Sn=···…····S1=×××…××××1=.
又当n=1时,S1=a1=1也成立,所以Sn=,
所以当n≥2时,an=Sn-Sn-1=-=n.
又a1=1也成立,所以an=n.
(2)由(1)知bn=(-1)n
=(-1)n,
所以Pn=-1-++--+…+(-1)n·+(-1)n=-1+
(-1)n,
所以|Pn+1|=< n>.
因为n为正整数,所以n的最小值是1 010.
感悟升华 此类问题多归结为解关于n的不等式解决.
【训练4】 (2021·名校仿真训练卷五)数列{an}中,a1=2,(n+1)(an+1-an)=2(an+n+1).
(1)求a2,a3的值;
(2)已知数列{an}的通项公式是an=n+1,an=n2+1,an=n2+n中的一个,设数列的前n项和为Sn,数列{an+1-an}的前n项和为Tn,若>360,求n的取值范围.
解 (1)∵(n+1)(an+1-an)=2(an+n+1),
∴an+1=an+2,
∴a2=a1+2=6,a3=a2+2=12.
(2)∵数列{an}的通项公式是an=n+1,an=n2+1,an=n2+n中的一个,且a2=6,
∴数列{an}的通项公式是an=n2+n=n(n+1).
由an=n(n+1)可得==-.
∴++…+=++…+=1-,
∴Sn=1-.
∵(a2-a1)+(a3-a2)+…+(an+1-an)=an+1-a1,
an=n(n+1),
∴(a2-a1)+(a3-a2)+…+(an+1-an)=n2+3n,
即Tn=n2+3n.
由>360得n2+4n-357>0,解得n>17或n<-21.
∵n是正整数,
∴所求n的取值范围为(17,+∞),且n是正整数.
1.设正项数列{an}满足a1=1,an+1=an+(n∈N*).
(1)求证:2≤a-a≤3;
(2)求证:≤≤.
证明 (1)因为a1=1及an+1=an+(n≥1),所以an≥1,所以0<≤1.因为a==a++2,
所以a-a=+2∈(2,3],即2≤a-a≤3.
(2)由(1)得2n
2.(2021·衢州、湖州、丽水质检)已知数列{an}的前n项和Sn=,且an>0(n∈N*).
(1)写出a1,a2,a3的值,并求出数列{an}的通项公式;
(2)设bn=,Tn为数列{bn}的前n项和,求证:
又因为an>0,所以a1=2,a1+a2=S2=,
解得a2=4,同理,a3=6.
当n≥2时,an=Sn-Sn-1=-,
即(an+an-1)(an-an-1-2)=0.
因为an>0,所以an-an-1-2=0,即an-an-1=2,
所以数列{an}是首项为2,公差为2的等差数列,
故an=2n.
(2)证明 由(1)可得Sn=n(n+1),bn=,
所以bn>n,Tn>.
又bn=<=n+,
所以Tn<+=.
综上,
(1)求数列{an},{bn}的通项公式;
(2)若数列{cn}满足ancn=bn+2,求证:c1+c2+…+cn<.
(1)解 ∵a1=1,an=1+an-1,
∴an-an-1=1(n>1),
∴数列{an}是以1为首项,1为公差的等差数列,
∴an=n.
∵1+a1b1+a2b2+…+an-1bn-1=an,①
∴1+a1b1+a2b2+…+anbn=an+1,②
由②-①得anbn=an+1-an=1,
又∵an=n,∴bn=.
(2)证明 ∵ancn=bn+2,an=n,bn=,
∴cn=·=,
∴c1+c2+…+cn=
=
=-<.
4.(2021·嘉兴二测)已知数列{an}的前n项和为Sn,且Sn=.公比大于0的等比数列{bn}的首项b1=1,且b2+b3=20.
(1)求数列{an}和{bn}的通项公式;
(2)若cn=,求证:c1+c2+c3+…+cn<(n∈N*).
(1)解 当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=-=n.
当n=1时也满足上式,所以an=n.
设等比数列{bn}的公比为q>0,
则b2+b3=b1q+b1q2=q+q2=20,
解得q=4或q=-5(舍去),所以bn=4n-1.
(2)证明 由(1)知cn=,===,c1=c2=1,c3=.
当n≥2时,≤,
所以c1+c2+c3+c4+…+cn≤1+1+++…+=1+=1+<1+<.
5.已知等差数列{an}的公差d≠0,a1=25,且a1,a11,a13成等比数列.
(1)求使不等式an≥0成立的最大自然数n;
(2)记数列的前n项和为Tn,求证:-≤Tn≤.
(1)解 由题意可知a=a1·a13,
即(a1+10d)2=a1·(a1+12d),
∴d(2a1+25d)=0.
又a1=25,d≠0,
∴d=-2,∴an=-2n+27,
∴-2n+27≥0,∴n≤13.5,
故满足题意的最大自然数为n=13.
(2)证明 =
=-,
∴Tn=+++…+
=-+
=-
=-+.
从而当n≤12时,Tn=-+单调递增,且Tn>0;
当n≥13时,Tn=-+单调递增,且Tn<0,
∴T13≤Tn≤T12,由T12=,T13=-,
∴-≤Tn≤.
6.(2021·金华十校期末调研测试)已知数列{an}的前n项和为Sn,Sn是-3和3an的等差中项.
(1)求数列{an}的通项公式;
(2)若··…·≥λ对任意的正整数n恒成立,求实数λ的取值范围.
解 (1)由题意得2Sn=-3+3an,
则当n≥2时,2Sn-1=-3+3an-1,
∴当n≥2时,an=3an-1.
又由2S1=-3+3a1得a1=3,
∴数列{an}是以3为首项,3为公比的等比数列,
∴an=3n.
(2)由题意知2Sn=-3+3an,得=,
得··…·=··…·,
∴λ≤.
设bn=.
∵an=3n,∴bn>0,
∴=>1,
∴{bn}是递增数列,最小项是b1==,
∴λ≤,即实数λ的取值范围为 .
7.(2021·绍兴上虞区期末调测)在数列{an}中,已知a1=1,an+1=an+2n-1.
(1)求数列{an}的通项公式;
(2)记bn=an+(1-λ)n,且数列{bn}的前n项和为Sn,若S2为数列{Sn}中的最小项,求λ的取值范围.
解 (1)∵a2=a1+2-1,
a3=a2+22-1,
…
an-1=an-2+2n-2-1,
an=an-1+2n-1-1,
累加可得an-a1=2n-2-(n-1)(n≥2),
∴an=2n-n,
当n=1时,a1=2-1=1,则an=2n-n.
(2)由(1)得bn=an+(1-λ)n=2n-λn,
∴Sn=2n+1-2-λ≥S2=6-3λ,
即2n+1-8≥λ.
当n=1时,得-4≥-2λ,∴λ≥2;
当n=2时,λ∈R;
当n≥3时,得-3>0,∴λ≤.
令f(n)=,
则f(n+1)-f(n)=-=,
当n≥4时,n2-n-8>0,∴f(n+1)>f(n),
又可验证当n=3时,f(4)-f(3)>0也成立,
∴当n≥3时,数列{f(n)}为递增数列,
∴f(n)min=f(3)=,即λ≤.
综上所述,λ的取值范围为.
8.(2021·宁波期末)已知等差数列{an}满足a2=2a1,a4+a5=9,Sn为等比数列{bn}的前n项和,2Sn+1=Sn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn=证明:c1+c2+c3+…+cn<.
(1)解 由题意得解得
∴an=n,即数列{an}的通项公式为an=n.
由2Sn+1=Sn+2,得
两式相减整理得:2b3=b2,
∴q=,b1=1,
∴bn=,即数列{bn}的通项公式为bn=.
(2)证明 (应用放缩和错位相减法求和证明不等式)
令Cn=c1+c2+c3+…+cn,Ak=c1+c3+…+c2k-1,
Bk=c2+c4+…+c2k,
则Ak=,
利用错位相减法可求得Ak=-<.
又∵(2k)2>(2k-1)(2k+1),
∴Bk=++…+
<<=.
∴Bk=++…+<,
当n为偶数时,
Cn=A+B<-+<;
当n为奇数时,
Cn=A+B<-+<.
综上,Cn<,即c1+c2+c3+…+cn<.
本资料分享自新人教版高中数学资源大全QQ群483122854 期待你的加入与分享
同课章节目录
