高考命题研析 第1讲 新高考新题型 课件(共28张PPT)
文档属性
| 名称 | 高考命题研析 第1讲 新高考新题型 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 16:09:09 | ||
图片预览







文档简介
(共28张PPT)
开篇 高考命题研析
第1讲 新高考新题型
随着新教材的广泛使用,“破定势,考真功”的命题理念越来越受到重视,《中国高考评价体系》指出命制结论开放、解题方法多样、答案不唯一的试题,增强试题的开放性和探究性,引导学生打破常规进行独立思考和判断,提出解决问题的方案,如多选题、一题双空题、开放型、结构不良型解答题在新高考中的呈现.
题型聚焦 分类研析
内容索引
题型聚焦 分类研析
新题型一 多选题
多选题常对多个对象(知识点)进行考查,也可对同一对象从不同角度进行考查,解法灵活,如直推法、验证法、反例法、数形结合法等均可使用,但必须对每个选项作出正确判断,才能得出正确答案.
【例1】 (1)(2021·新高考Ⅰ卷)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( )
A.两组样本数据的样本平均数相同 B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同 D.两组样本数据的样本极差相同
CD
显然第一组数据与第二组数据的中位数相差c,B错误;
因为D(y)=12·D(x)=D(x),故两组样本数据的方差相同,C项正确;
由极差的定义知:若第一组的极差为xmax-xmin,则第二组的极差为ymax-ymin=xmax-xmin,故两组样本数据的极差相同,D项正确.
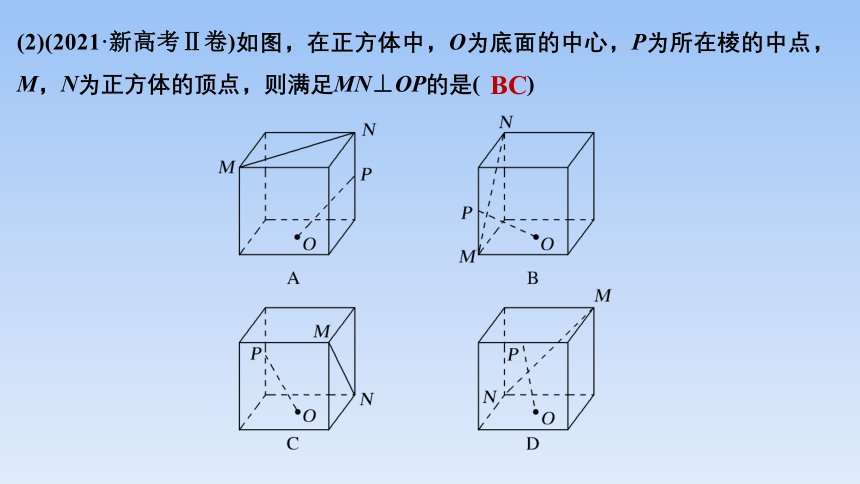
(2)(2021·新高考Ⅱ卷)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点,则满足MN⊥OP的是( )
BC
解析 设正方体的棱长为2.
对于A,如图(1)所示,连接AC,则MN∥AC,故∠POC(或其补角)为异面直线OP,MN所成的角.在直角三角形OPC中,∠POC为锐角,故MN⊥OP不成立,故A错误;
图(1)
对于B,如图(2)所示,取MT的中点为Q,连接PQ,OQ,则OQ⊥MT,PQ⊥MN.由正方体SBCNMADT可得SM⊥平面MADT,而OQ 平面MADT,故SM⊥OQ,又SM∩MT=M,SM,MT 平面SNTM,故OQ⊥平面SNTM,又MN 平面SNTM,所以OQ⊥MN,又OQ∩PQ=Q,OQ,PQ 平面OPQ,所以MN⊥平面OPQ,又OP 平面OPQ,故MN⊥OP,故B正确;
图(2)
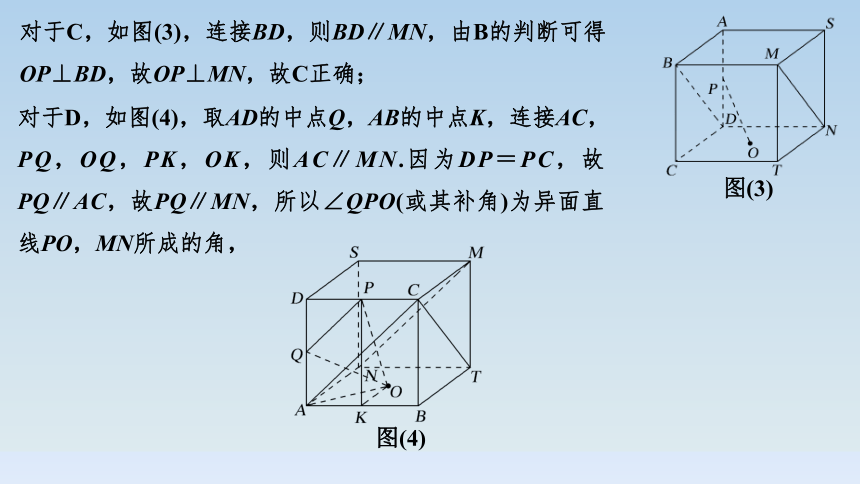
对于C,如图(3),连接BD,则BD∥MN,由B的判断可得OP⊥BD,故OP⊥MN,故C正确;
图(3)
对于D,如图(4),取AD的中点Q,AB的中点K,连接AC,PQ,OQ,PK,OK,则AC∥MN.因为DP=PC,故PQ∥AC,故PQ∥MN,所以∠QPO(或其补角)为异面直线PO,MN所成的角,
图(4)
(3)(2021·新高考Ⅰ卷)已知O为坐标原点,点P1(cos α,sin α),P2(cos β,-sin β),P3(cos(α+β),sin(α+β)),A(1,0),则( )
AC
新题型二 多空题与开放型填空题
1.多空题分为三类:
(1)并列式(两空相连).根据题设条件,利用同一解题思路和过程,可以一次性得出两个空的答案,两空并答,题目比较简单.会便全会,这类题目在高考中一般涉及较少,常考查一些基本量的求解;
(2)分列式(一空一答).两空的设问相当于一个题目背景下的两道小填空题,两问之间没什么具体联系,各自成题,是对于多个知识点或某知识点的多个角度的考查;两问之间互不干扰,不会其中一问,照样可以答出另一问;
(3)递进式(逐空解答).两空之间有着一定联系,一般是第二空需要借助第一空的结果再进行作答,第一空是解题的关键,也是解答第二空的基础;
2.开放型填空题的特点是正确的答案不唯一,一般可分为:
(1)探索型(一是条件探索型,二是结论探索型);
(2)信息迁移型;
(3)组合型等类型.
【例2】 (1)(2021·北京卷)已知a=(2,1),b=(2,-1),c=(0,1),则(a+b)·c=________;a·b=________.
0
3
解析 计算可得(a+b)·c=(4,0)·(0,1)=0,a·b=4-1=3.
5
解析 依题意得,S1=120×2=240(dm2);
S2=60×3=180(dm2);
所以S3=30×4=120(dm2);
(2)(2021·新高考Ⅱ卷)写出一个同时具有下列性质①②③的函数f(x):___________________________________________.
①f(x1x2)=f(x1)f(x2);②当x∈(0,+∞)时,f′(x)>0;③f′(x)是奇函数.
f(x)=x4(答案不唯一,f(x)=x2n(n∈N*)均满足)
解析 取f(x)=x4,
f′(x)=4x3,x>0时有f′(x)>0,满足②;
f′(x)=4x3的定义域为R,
又f′(-x)=-4x3=-f′(x),故f′(x)是奇函数,满足③.
新题型三 结构不良型解答题
(1)结构不良型解答题多出现在三角函数和解三角形、数列两部分内容,但有时也出现在其他章节,有三选一和三选二两种类型.
(2)解答此类题型,要注意仔细审视条件,切忌浅尝辄止,反复变更条件解答.
因此,选条件①时问题中的三角形存在,此时c=1.
方案二:选条件②.
方案三:选条件③.
(1)求B的大小;
又c=2bcos B,所以sin C=2sin Bcos B=sin 2B,
(2)在三个条件中选择一个作为已知,使△ABC存在且唯一确定,并求BC边上的中线的长度.
设BC中点为D,则在△ABD中,由余弦定理,得
设BC中点为D,则在△ABD中,由余弦定理,得
开篇 高考命题研析
第1讲 新高考新题型
随着新教材的广泛使用,“破定势,考真功”的命题理念越来越受到重视,《中国高考评价体系》指出命制结论开放、解题方法多样、答案不唯一的试题,增强试题的开放性和探究性,引导学生打破常规进行独立思考和判断,提出解决问题的方案,如多选题、一题双空题、开放型、结构不良型解答题在新高考中的呈现.
题型聚焦 分类研析
内容索引
题型聚焦 分类研析
新题型一 多选题
多选题常对多个对象(知识点)进行考查,也可对同一对象从不同角度进行考查,解法灵活,如直推法、验证法、反例法、数形结合法等均可使用,但必须对每个选项作出正确判断,才能得出正确答案.
【例1】 (1)(2021·新高考Ⅰ卷)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( )
A.两组样本数据的样本平均数相同 B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同 D.两组样本数据的样本极差相同
CD
显然第一组数据与第二组数据的中位数相差c,B错误;
因为D(y)=12·D(x)=D(x),故两组样本数据的方差相同,C项正确;
由极差的定义知:若第一组的极差为xmax-xmin,则第二组的极差为ymax-ymin=xmax-xmin,故两组样本数据的极差相同,D项正确.
(2)(2021·新高考Ⅱ卷)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点,则满足MN⊥OP的是( )
BC
解析 设正方体的棱长为2.
对于A,如图(1)所示,连接AC,则MN∥AC,故∠POC(或其补角)为异面直线OP,MN所成的角.在直角三角形OPC中,∠POC为锐角,故MN⊥OP不成立,故A错误;
图(1)
对于B,如图(2)所示,取MT的中点为Q,连接PQ,OQ,则OQ⊥MT,PQ⊥MN.由正方体SBCNMADT可得SM⊥平面MADT,而OQ 平面MADT,故SM⊥OQ,又SM∩MT=M,SM,MT 平面SNTM,故OQ⊥平面SNTM,又MN 平面SNTM,所以OQ⊥MN,又OQ∩PQ=Q,OQ,PQ 平面OPQ,所以MN⊥平面OPQ,又OP 平面OPQ,故MN⊥OP,故B正确;
图(2)
对于C,如图(3),连接BD,则BD∥MN,由B的判断可得OP⊥BD,故OP⊥MN,故C正确;
图(3)
对于D,如图(4),取AD的中点Q,AB的中点K,连接AC,PQ,OQ,PK,OK,则AC∥MN.因为DP=PC,故PQ∥AC,故PQ∥MN,所以∠QPO(或其补角)为异面直线PO,MN所成的角,
图(4)
(3)(2021·新高考Ⅰ卷)已知O为坐标原点,点P1(cos α,sin α),P2(cos β,-sin β),P3(cos(α+β),sin(α+β)),A(1,0),则( )
AC
新题型二 多空题与开放型填空题
1.多空题分为三类:
(1)并列式(两空相连).根据题设条件,利用同一解题思路和过程,可以一次性得出两个空的答案,两空并答,题目比较简单.会便全会,这类题目在高考中一般涉及较少,常考查一些基本量的求解;
(2)分列式(一空一答).两空的设问相当于一个题目背景下的两道小填空题,两问之间没什么具体联系,各自成题,是对于多个知识点或某知识点的多个角度的考查;两问之间互不干扰,不会其中一问,照样可以答出另一问;
(3)递进式(逐空解答).两空之间有着一定联系,一般是第二空需要借助第一空的结果再进行作答,第一空是解题的关键,也是解答第二空的基础;
2.开放型填空题的特点是正确的答案不唯一,一般可分为:
(1)探索型(一是条件探索型,二是结论探索型);
(2)信息迁移型;
(3)组合型等类型.
【例2】 (1)(2021·北京卷)已知a=(2,1),b=(2,-1),c=(0,1),则(a+b)·c=________;a·b=________.
0
3
解析 计算可得(a+b)·c=(4,0)·(0,1)=0,a·b=4-1=3.
5
解析 依题意得,S1=120×2=240(dm2);
S2=60×3=180(dm2);
所以S3=30×4=120(dm2);
(2)(2021·新高考Ⅱ卷)写出一个同时具有下列性质①②③的函数f(x):___________________________________________.
①f(x1x2)=f(x1)f(x2);②当x∈(0,+∞)时,f′(x)>0;③f′(x)是奇函数.
f(x)=x4(答案不唯一,f(x)=x2n(n∈N*)均满足)
解析 取f(x)=x4,
f′(x)=4x3,x>0时有f′(x)>0,满足②;
f′(x)=4x3的定义域为R,
又f′(-x)=-4x3=-f′(x),故f′(x)是奇函数,满足③.
新题型三 结构不良型解答题
(1)结构不良型解答题多出现在三角函数和解三角形、数列两部分内容,但有时也出现在其他章节,有三选一和三选二两种类型.
(2)解答此类题型,要注意仔细审视条件,切忌浅尝辄止,反复变更条件解答.
因此,选条件①时问题中的三角形存在,此时c=1.
方案二:选条件②.
方案三:选条件③.
(1)求B的大小;
又c=2bcos B,所以sin C=2sin Bcos B=sin 2B,
(2)在三个条件中选择一个作为已知,使△ABC存在且唯一确定,并求BC边上的中线的长度.
设BC中点为D,则在△ABD中,由余弦定理,得
设BC中点为D,则在△ABD中,由余弦定理,得
同课章节目录
