第2讲 新情境新命题(共37张PPT)
文档属性
| 名称 | 第2讲 新情境新命题(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 11:16:14 | ||
图片预览










文档简介
(共37张PPT)
开篇 高考命题研析
第2讲 新情境新命题
新情境试题重视数学本质,突出理性思维、数学应用、数学探究、数学文化的引领作用,是新高考考查的热点内容.试题往往使用贴近时代、贴近社会、贴近生活的素材,以日常生活、工业生产、国家发展、社会进步中的实际问题为背景,考查学生运用数学知识解决实际问题的能力,让学生充分感受到数学的应用价值,强调以素养为导向,深受命题专家的青睐.试题多以图、表、文并用的方式呈现,各种题型都有可能出现.
命题热点 分类研析
内容索引
命题热点 分类研析
新情境一 注重五育并举,培育时代新人
【例1】 (2021·新高考Ⅱ卷)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36 000 km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O、半径r为6 400 km的球,其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度的最大值为α,记卫星信号覆盖地球表面的面积为S=2πr2(1-cos α)(单位:km2),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
C
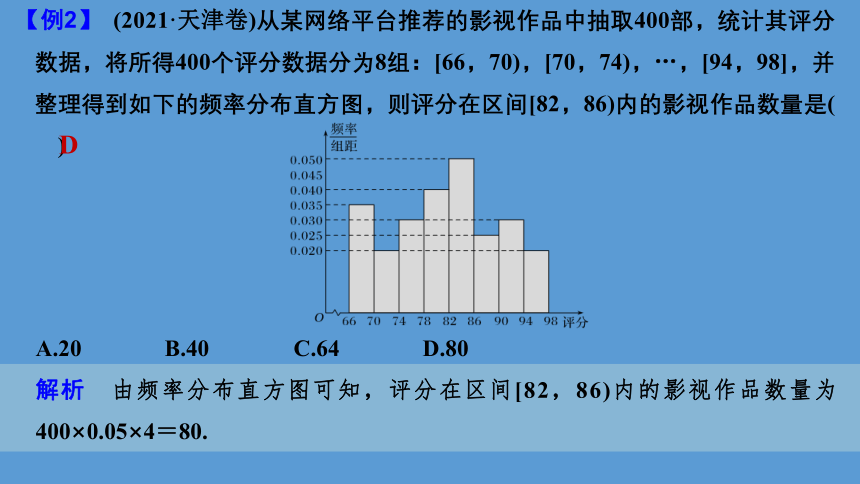
【例2】 (2021·天津卷)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[66,70),[70,74),…,[94,98],并整理得到如下的频率分布直方图,则评分在区间[82,86)内的影视作品数量是( )
D
A.20 B.40 C.64 D.80
解析 由频率分布直方图可知,评分在区间[82,86)内的影视作品数量为400×0.05×4=80.
【例3】 学校开展劳动实习课,某班将在如图所示的曲边梯形ABCD的场地中建矩形花圃EBFH,经建系测绘,收集到以下信息:D(0,0),A(2,0),B(2,8),C(-2,8).曲线CD可以近似看作函数y=-x3图象的一段,AD⊥AB,AD∥BC.现要求矩形花圃EBFH的顶点E,F,H分别落在边AB,边BC和曲边CD上,若点H的横坐标为x且x∈(-2,-1],花圃EBFH的面积S与x的函数关系式记为S(x),则下列四个结论:
①S(x)在(-2,-1]上单调递增;
②S(x)在(-2,-1]上先单调递增再单调递减;
③S(x)在(-2,-1)上存在最大值;
④S(x)的最大值为21.
其中正确的命题序号为( )
A.①③ B.①④ C.②④ D.③④
B
解析 S(x)=(2-x)(8+x3),x∈(-2,-1],
S′(x)=-2(2x3-3x2+4).
令f(x)=-2(2x3-3x2+4),x∈(-2,-1],
则f′(x)=-12x(x-1).
因为x∈(-2,-1],所以f′(x)=-12x(x-1)<0,
所以S′(x)在(-2,-1]上单调递减,
所以S′(x)≥S′(-1)=2>0.
所以S(x)在(-2,-1]上单调递增,
S(x)max=S(-1)=21.
因此命题①④正确.
新情境二 聚焦社会热点,彰显责任担当
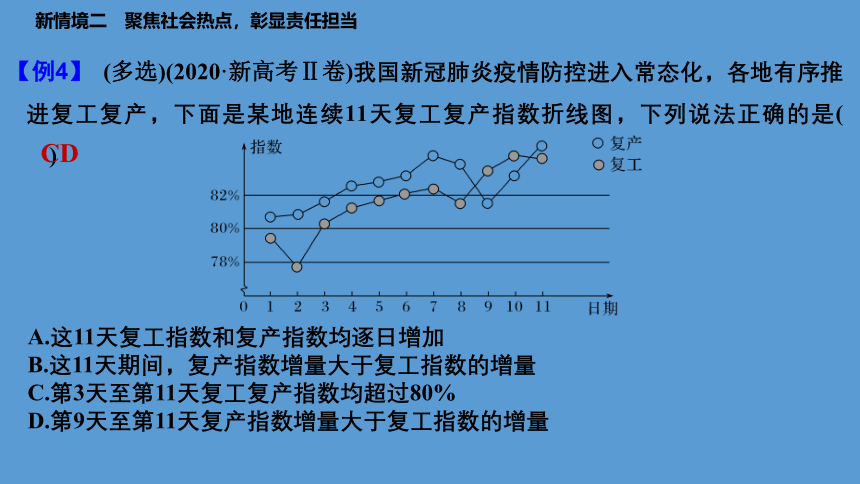
【例4】 (多选)(2020·新高考Ⅱ卷)我国新冠肺炎疫情防控进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
CD
A.这11天复工指数和复产指数均逐日增加
B.这11天期间,复产指数增量大于复工指数的增量
C.第3天至第11天复工复产指数均超过80%
D.第9天至第11天复产指数增量大于复工指数的增量
解析 由图可知,第1天到第2天复工指数减少,第7天到第8天复工指数减少,第10天到第11天复工指数减少,第8天到第9天复产指数减少,故A错误;由图可知,第1天的复产指数与复工指数的差大于第11天的复产指数与复工指数的差,所以这11天期间,复产指数增量小于复工指数的增量,故B错误;由图可知,第3天至第11天复工复产指数均超过80%,故C正确;由图可知,第9天至第11天复产指数增量大于复工指数的增量,故D正确;故选CD.
A.1.5 B.1.2 C.0.8 D.0.6
C
新情境三 弘扬传统文化,增强民族自信
【例6】 (2021·全国乙卷)魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”,则海岛的高AB=( )
A
【例7】 (2020·新高考Ⅰ卷)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
B
A.20° B.40°
C.50° D.90°
解析 示意图如图所示,⊙O所在平面为地球赤道所在平面,⊙O1所在平面为点A处的日晷的晷面所在的平面,由点A处的纬度为北纬40°可知∠OAO1=40°,又点A处的水平面与OA垂直,晷针AC与⊙O1所在的平面垂直,则∠CAB=∠OAO1=40°,故晷针AC与点A处的水平面所成角为40°.故选B.
【例8】 攒尖是古代中国建筑中屋顶的一种结构形式.依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.以如图所示的建筑物为例,它属重檐四角攒尖,它的上层轮廓可近似看作一个正四棱锥,若此正四棱锥的侧面积是底面积的3倍,则此正四棱锥的内切球半径与底面边长比值为( )
B
解析 设正四棱锥的底边为a,斜高为h,
则底面积为a2,所以该正四棱锥的侧面积为3a2,
设该正四棱锥的内切球的半径为r,作出示意图,如图所示,其中E,F分别为AB,CD的中点,H为底面的中点,PF与球O相切于点G.
新情境四 贴近现实生活,培养应用意识
【例9】 (2021·北京卷)对24小时内降水在平地上的积水厚度(mm)进行如下定义:
B
0~10 10~25 25~50 50~100
小雨 中雨 大雨 暴雨
小明用一个圆锥形容器接了24小时的雨水,则这一天的雨水属于哪个等级( )
A.小雨 B.中雨
C.大雨 D.暴雨
【例10】 (2021·全国甲卷)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
C
解析 对于A,根据频率分布直方图可知,该地农户家庭年收入低于4.5万元的农户比率估计为(0.02+0.04)×1×100%=6%,故A正确;
对于B,根据频率分布直方图可知,该地农户家庭年收入不低于10.5万元的农户比率估计为(0.04+0.02+0.02+0.02)×1×100%=10%,故B正确;
对于C,根据频率分布直方图可知,该地农户家庭年收入的平均值估计为3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68(万元),故C错误;
对于D,根据频率分布直方图可知,该地农户家庭年收入介于4.5万元至8.5万元之间的农户比率估计为(0.10+0.14+0.20+0.20)×1×100%=64%>50%,故D正确.
新情境五 重视科技创新,培养探索精神
AC
解析 对于A,当n=1时,p1=1,H(X)=-1×log21=0,故A正确;
对于D,法一 当n=2m时,
同理可证p2log2p2+p2m-1log2p2m-1<(p2+p2m-1)log2(p2+p2m-1),…,
pmlog2pm+pm+1log2pm+1<(pm+pm+1)log2(pm+pm+1),
所以H(X)>H(Y),故D错误.
P(Y=1)=1,H(Y)=-log21=0,
∴H(X)>H(Y),故D错误.
A.346 B.373
C.446 D.473
B
新情境六 关注学科融合,突出理性思维
A.20天 B.30天 C.45天 D.60天
D
【例14】 汽车智能辅助驾驶已开始得到应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车.若将报警时间划分为4段,分别为准备时间t0、人的反应时间t1、系统反应时间t2、制动时间t3,相应的距离(单位:米)分别为d0,d1,d2,d3,如图所示.当车速为v(单位:米/秒),且v∈(0,33.3]时,通过大数据统计分析得到表中给出的数据(其中系数k随地面湿滑程度等路面情况而变化,k∈[1,2]).
(1)请写出报警距离d与车速v之间的函数关系式,并求出当k=1,在汽车达到报警距离时,若人和系统均未采取任何制动措施,仍以此速度行驶的情况下,汽车撞上固定障碍物的最短时间(精确到0.1秒);
解 由题意得d(v)=d0+d1+d2+d3,
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于50米,则汽车的行驶速度限制在多少千米/时内?
解 根据题意得, k∈[1,2],d(v)<50恒成立,
解得-40所以00),
所以汽车的行驶速度应限制在72千米/时内.
开篇 高考命题研析
第2讲 新情境新命题
新情境试题重视数学本质,突出理性思维、数学应用、数学探究、数学文化的引领作用,是新高考考查的热点内容.试题往往使用贴近时代、贴近社会、贴近生活的素材,以日常生活、工业生产、国家发展、社会进步中的实际问题为背景,考查学生运用数学知识解决实际问题的能力,让学生充分感受到数学的应用价值,强调以素养为导向,深受命题专家的青睐.试题多以图、表、文并用的方式呈现,各种题型都有可能出现.
命题热点 分类研析
内容索引
命题热点 分类研析
新情境一 注重五育并举,培育时代新人
【例1】 (2021·新高考Ⅱ卷)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36 000 km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O、半径r为6 400 km的球,其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度的最大值为α,记卫星信号覆盖地球表面的面积为S=2πr2(1-cos α)(单位:km2),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
C
【例2】 (2021·天津卷)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[66,70),[70,74),…,[94,98],并整理得到如下的频率分布直方图,则评分在区间[82,86)内的影视作品数量是( )
D
A.20 B.40 C.64 D.80
解析 由频率分布直方图可知,评分在区间[82,86)内的影视作品数量为400×0.05×4=80.
【例3】 学校开展劳动实习课,某班将在如图所示的曲边梯形ABCD的场地中建矩形花圃EBFH,经建系测绘,收集到以下信息:D(0,0),A(2,0),B(2,8),C(-2,8).曲线CD可以近似看作函数y=-x3图象的一段,AD⊥AB,AD∥BC.现要求矩形花圃EBFH的顶点E,F,H分别落在边AB,边BC和曲边CD上,若点H的横坐标为x且x∈(-2,-1],花圃EBFH的面积S与x的函数关系式记为S(x),则下列四个结论:
①S(x)在(-2,-1]上单调递增;
②S(x)在(-2,-1]上先单调递增再单调递减;
③S(x)在(-2,-1)上存在最大值;
④S(x)的最大值为21.
其中正确的命题序号为( )
A.①③ B.①④ C.②④ D.③④
B
解析 S(x)=(2-x)(8+x3),x∈(-2,-1],
S′(x)=-2(2x3-3x2+4).
令f(x)=-2(2x3-3x2+4),x∈(-2,-1],
则f′(x)=-12x(x-1).
因为x∈(-2,-1],所以f′(x)=-12x(x-1)<0,
所以S′(x)在(-2,-1]上单调递减,
所以S′(x)≥S′(-1)=2>0.
所以S(x)在(-2,-1]上单调递增,
S(x)max=S(-1)=21.
因此命题①④正确.
新情境二 聚焦社会热点,彰显责任担当
【例4】 (多选)(2020·新高考Ⅱ卷)我国新冠肺炎疫情防控进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
CD
A.这11天复工指数和复产指数均逐日增加
B.这11天期间,复产指数增量大于复工指数的增量
C.第3天至第11天复工复产指数均超过80%
D.第9天至第11天复产指数增量大于复工指数的增量
解析 由图可知,第1天到第2天复工指数减少,第7天到第8天复工指数减少,第10天到第11天复工指数减少,第8天到第9天复产指数减少,故A错误;由图可知,第1天的复产指数与复工指数的差大于第11天的复产指数与复工指数的差,所以这11天期间,复产指数增量小于复工指数的增量,故B错误;由图可知,第3天至第11天复工复产指数均超过80%,故C正确;由图可知,第9天至第11天复产指数增量大于复工指数的增量,故D正确;故选CD.
A.1.5 B.1.2 C.0.8 D.0.6
C
新情境三 弘扬传统文化,增强民族自信
【例6】 (2021·全国乙卷)魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”,则海岛的高AB=( )
A
【例7】 (2020·新高考Ⅰ卷)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
B
A.20° B.40°
C.50° D.90°
解析 示意图如图所示,⊙O所在平面为地球赤道所在平面,⊙O1所在平面为点A处的日晷的晷面所在的平面,由点A处的纬度为北纬40°可知∠OAO1=40°,又点A处的水平面与OA垂直,晷针AC与⊙O1所在的平面垂直,则∠CAB=∠OAO1=40°,故晷针AC与点A处的水平面所成角为40°.故选B.
【例8】 攒尖是古代中国建筑中屋顶的一种结构形式.依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.以如图所示的建筑物为例,它属重檐四角攒尖,它的上层轮廓可近似看作一个正四棱锥,若此正四棱锥的侧面积是底面积的3倍,则此正四棱锥的内切球半径与底面边长比值为( )
B
解析 设正四棱锥的底边为a,斜高为h,
则底面积为a2,所以该正四棱锥的侧面积为3a2,
设该正四棱锥的内切球的半径为r,作出示意图,如图所示,其中E,F分别为AB,CD的中点,H为底面的中点,PF与球O相切于点G.
新情境四 贴近现实生活,培养应用意识
【例9】 (2021·北京卷)对24小时内降水在平地上的积水厚度(mm)进行如下定义:
B
0~10 10~25 25~50 50~100
小雨 中雨 大雨 暴雨
小明用一个圆锥形容器接了24小时的雨水,则这一天的雨水属于哪个等级( )
A.小雨 B.中雨
C.大雨 D.暴雨
【例10】 (2021·全国甲卷)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
C
解析 对于A,根据频率分布直方图可知,该地农户家庭年收入低于4.5万元的农户比率估计为(0.02+0.04)×1×100%=6%,故A正确;
对于B,根据频率分布直方图可知,该地农户家庭年收入不低于10.5万元的农户比率估计为(0.04+0.02+0.02+0.02)×1×100%=10%,故B正确;
对于C,根据频率分布直方图可知,该地农户家庭年收入的平均值估计为3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68(万元),故C错误;
对于D,根据频率分布直方图可知,该地农户家庭年收入介于4.5万元至8.5万元之间的农户比率估计为(0.10+0.14+0.20+0.20)×1×100%=64%>50%,故D正确.
新情境五 重视科技创新,培养探索精神
AC
解析 对于A,当n=1时,p1=1,H(X)=-1×log21=0,故A正确;
对于D,法一 当n=2m时,
同理可证p2log2p2+p2m-1log2p2m-1<(p2+p2m-1)log2(p2+p2m-1),…,
pmlog2pm+pm+1log2pm+1<(pm+pm+1)log2(pm+pm+1),
所以H(X)>H(Y),故D错误.
P(Y=1)=1,H(Y)=-log21=0,
∴H(X)>H(Y),故D错误.
A.346 B.373
C.446 D.473
B
新情境六 关注学科融合,突出理性思维
A.20天 B.30天 C.45天 D.60天
D
【例14】 汽车智能辅助驾驶已开始得到应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车.若将报警时间划分为4段,分别为准备时间t0、人的反应时间t1、系统反应时间t2、制动时间t3,相应的距离(单位:米)分别为d0,d1,d2,d3,如图所示.当车速为v(单位:米/秒),且v∈(0,33.3]时,通过大数据统计分析得到表中给出的数据(其中系数k随地面湿滑程度等路面情况而变化,k∈[1,2]).
(1)请写出报警距离d与车速v之间的函数关系式,并求出当k=1,在汽车达到报警距离时,若人和系统均未采取任何制动措施,仍以此速度行驶的情况下,汽车撞上固定障碍物的最短时间(精确到0.1秒);
解 由题意得d(v)=d0+d1+d2+d3,
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于50米,则汽车的行驶速度限制在多少千米/时内?
解 根据题意得, k∈[1,2],d(v)<50恒成立,
解得-40
所以汽车的行驶速度应限制在72千米/时内.
同课章节目录
