专题三 立体几何:拓展优化 立体几何中的动态、最值问题 课件(共21张PPT)
文档属性
| 名称 | 专题三 立体几何:拓展优化 立体几何中的动态、最值问题 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 968.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 21:27:27 | ||
图片预览








文档简介
(共21张PPT)
上篇 专题三 立体几何
拓展优化 立体几何中的动态、最值问题
立体几何着重研究空间点、线、面之间的位置关系,几何图形折叠、剪拼、拆合等动态问题,涉及空间图形有关的线段、角、体积的最值,是高考命题的热点.求解的关键是在平面图形直观认识的基础上,分析动态问题,把握空间位置关系.题目能较好地考查学生的空间想象能力、逻辑推理与数学运算等数学素养.
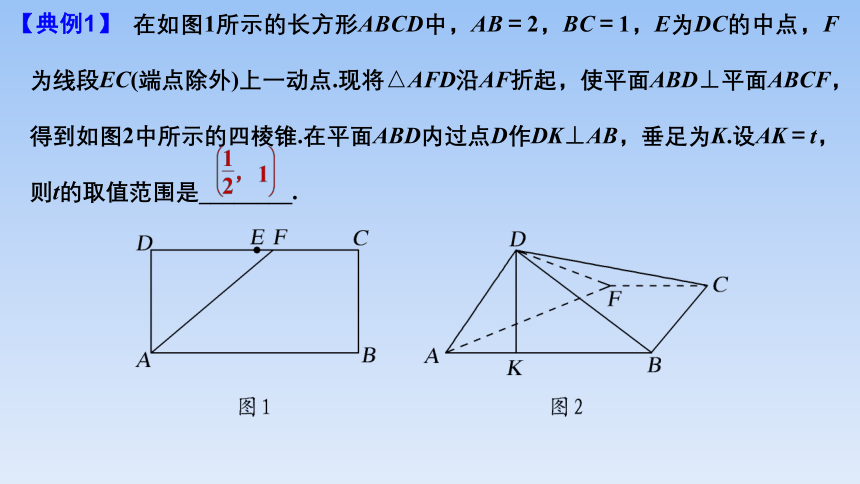
【典例1】 在如图1所示的长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABCF,得到如图2中所示的四棱锥.在平面ABD内过点D作DK⊥AB,垂足为K.设AK=t,则t的取值范围是________.
思路点拨 设FC=x(0解析 过F作FM⊥AB,交AB于M,连接FK(图略).
设FC=x,0易知AK在Rt△ADK中,DK2=1-t2,
在Rt△FMK中,FK2=1+(2-t-x)2.
因为平面ABD⊥平面ABCF,平面ABD∩平面ABCF=AB,DK⊥AB,DK 平面ABD,
所以DK⊥平面ABCF,所以DK⊥FK.
在Rt△DFK中,DF=2-x,DK2+FK2=DF2,
所以1-t2+1+(2-t-x)2=(2-x)2,
1.本题是一个动态的翻折问题,需要考生发现其中不变的垂直关系,从而得出相关变量间的关系,最终转化成函数的值域问题.
2.求解的关键是根据相关的定理对图形中位置关系进行精准判断,抓住不变量,另外注意变量x∈(0,1)的范围.
点津突破
【典例2】 (2021·大连检测)已知某圆锥的母线长为3,底面半径为1,则该圆锥的体积为________.设线段AB为该圆锥底面圆的一条直径,一质点从A出发,沿着该圆锥的侧面运动,到达B点后再沿侧面回到A点,则该质点运动路径的最短长度为________.
思路点拨 根据公式可求得圆锥的体积,将圆锥侧面展开,连接AB,A′B,则该质点运动路径的最短长度为AB+A′B.
6
将圆锥侧面沿母线SA展开,如图所示.
由题意知点B是圆锥侧面展开后得到的扇形中弧AA′的中点,
可得AB=A′B=AS=3.
所以该质点运动路径的最短长度为AB+A′B=6.
1.求解圆锥侧面上质点运动路径的最短长度问题时,通常将圆锥侧面沿一条母线展开成扇形,在平面图形中分析、解决问题.
2.化曲为直是求解曲面上路径长度最短问题的关键,如本题,将曲面上A→B→A的路线转化为平面上A→B→A′的路线,则最短路径长度为AB+A′B.
点津突破
【典例3】 (2021·衡水调研)已知四面体ABCD的棱长满足AB=AC=BD=CD=2,BC=AD=1,现将四面体ABCD放入一个轴截面为等边三角形的圆锥中,使得四面体ABCD可以在圆锥中任意转动,则圆锥侧面积的最小值为________.
思路点拨 四面体ABCD可以在圆锥中任意转动可以转化为四面体ABCD在圆锥的内切球内,当圆锥的侧面积最小时,内切球也是四面体ABCD的外接球,故先求出四面体ABCD外接球的半径,再求出圆锥底面圆的半径及母线长即可得解.
解析 根据题意,只需四面体ABCD在圆锥的内切球内.
下面求四面体ABCD的外接球半径.
如图所示,分别取AD,BC的中点M,N,连接MN,MC.取MN的中点O,连接OB.
根据题意,可得O为四面体ABCD外接球的球心,且MN⊥BC,CM⊥AD.
本题将“四面体可以在圆锥中任意转动”转化为“四面体在圆锥的内切球内”,又通过“侧面积最小”将圆锥的内切球问题转化为四面体的外接球问题,从而转化为如何确定四面体外接球的球心及半径问题.灵活运用转化思想是求解本题的关键.
点津突破
[跟踪演练]
1.(多选)如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,P是A1B上的一动点,则( )
AD
连接A1C1,BC1,得△A1BC1,以A1B所在直线为轴,将△A1BC1所在平面旋转到平面ABB1A1,设点C1的新位置为C′,连接AC′(图略),则AC′即为所求的最小值.
2.(2021·江南十校联考)设P,Q,R分别是长方体ABCDA1B1C1D1的棱AB,CC1,C1D1的中点,且BC=CC1=1,AB=2,M是底面ABCD上的一个动点,若直线D1M与平面PQR没有公共点,则三角形BB1M面积的最小值为________.
解析 如图所示,分别取A1D1,AA1,BC的中点E,F,G,连接EF,FP,PG,QG,ER,易知平面EFPGQR与平面PQR共面.连接AD1,AC,CD1,易得平面AD1C∥平面EFPGQR,故M在线段AC上运动.
图1
在四面体ABCD中,三角形ABC和三角形DAC均为直角三角形,设点O为AC的中点,如图2,连接OB,OD,则AO=OC=OB=OD=1,即点O为四面体ABCD外接球的球心,则外接球的半径R=1,
图2
因为二面角DACB的平面角为θ,
且BF⊥AC,DE⊥AC,
拼一个春夏秋冬,博高考无怨无悔!
本节内容结束
上篇 专题三 立体几何
拓展优化 立体几何中的动态、最值问题
立体几何着重研究空间点、线、面之间的位置关系,几何图形折叠、剪拼、拆合等动态问题,涉及空间图形有关的线段、角、体积的最值,是高考命题的热点.求解的关键是在平面图形直观认识的基础上,分析动态问题,把握空间位置关系.题目能较好地考查学生的空间想象能力、逻辑推理与数学运算等数学素养.
【典例1】 在如图1所示的长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABCF,得到如图2中所示的四棱锥.在平面ABD内过点D作DK⊥AB,垂足为K.设AK=t,则t的取值范围是________.
思路点拨 设FC=x(0
设FC=x,0
在Rt△FMK中,FK2=1+(2-t-x)2.
因为平面ABD⊥平面ABCF,平面ABD∩平面ABCF=AB,DK⊥AB,DK 平面ABD,
所以DK⊥平面ABCF,所以DK⊥FK.
在Rt△DFK中,DF=2-x,DK2+FK2=DF2,
所以1-t2+1+(2-t-x)2=(2-x)2,
1.本题是一个动态的翻折问题,需要考生发现其中不变的垂直关系,从而得出相关变量间的关系,最终转化成函数的值域问题.
2.求解的关键是根据相关的定理对图形中位置关系进行精准判断,抓住不变量,另外注意变量x∈(0,1)的范围.
点津突破
【典例2】 (2021·大连检测)已知某圆锥的母线长为3,底面半径为1,则该圆锥的体积为________.设线段AB为该圆锥底面圆的一条直径,一质点从A出发,沿着该圆锥的侧面运动,到达B点后再沿侧面回到A点,则该质点运动路径的最短长度为________.
思路点拨 根据公式可求得圆锥的体积,将圆锥侧面展开,连接AB,A′B,则该质点运动路径的最短长度为AB+A′B.
6
将圆锥侧面沿母线SA展开,如图所示.
由题意知点B是圆锥侧面展开后得到的扇形中弧AA′的中点,
可得AB=A′B=AS=3.
所以该质点运动路径的最短长度为AB+A′B=6.
1.求解圆锥侧面上质点运动路径的最短长度问题时,通常将圆锥侧面沿一条母线展开成扇形,在平面图形中分析、解决问题.
2.化曲为直是求解曲面上路径长度最短问题的关键,如本题,将曲面上A→B→A的路线转化为平面上A→B→A′的路线,则最短路径长度为AB+A′B.
点津突破
【典例3】 (2021·衡水调研)已知四面体ABCD的棱长满足AB=AC=BD=CD=2,BC=AD=1,现将四面体ABCD放入一个轴截面为等边三角形的圆锥中,使得四面体ABCD可以在圆锥中任意转动,则圆锥侧面积的最小值为________.
思路点拨 四面体ABCD可以在圆锥中任意转动可以转化为四面体ABCD在圆锥的内切球内,当圆锥的侧面积最小时,内切球也是四面体ABCD的外接球,故先求出四面体ABCD外接球的半径,再求出圆锥底面圆的半径及母线长即可得解.
解析 根据题意,只需四面体ABCD在圆锥的内切球内.
下面求四面体ABCD的外接球半径.
如图所示,分别取AD,BC的中点M,N,连接MN,MC.取MN的中点O,连接OB.
根据题意,可得O为四面体ABCD外接球的球心,且MN⊥BC,CM⊥AD.
本题将“四面体可以在圆锥中任意转动”转化为“四面体在圆锥的内切球内”,又通过“侧面积最小”将圆锥的内切球问题转化为四面体的外接球问题,从而转化为如何确定四面体外接球的球心及半径问题.灵活运用转化思想是求解本题的关键.
点津突破
[跟踪演练]
1.(多选)如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,P是A1B上的一动点,则( )
AD
连接A1C1,BC1,得△A1BC1,以A1B所在直线为轴,将△A1BC1所在平面旋转到平面ABB1A1,设点C1的新位置为C′,连接AC′(图略),则AC′即为所求的最小值.
2.(2021·江南十校联考)设P,Q,R分别是长方体ABCDA1B1C1D1的棱AB,CC1,C1D1的中点,且BC=CC1=1,AB=2,M是底面ABCD上的一个动点,若直线D1M与平面PQR没有公共点,则三角形BB1M面积的最小值为________.
解析 如图所示,分别取A1D1,AA1,BC的中点E,F,G,连接EF,FP,PG,QG,ER,易知平面EFPGQR与平面PQR共面.连接AD1,AC,CD1,易得平面AD1C∥平面EFPGQR,故M在线段AC上运动.
图1
在四面体ABCD中,三角形ABC和三角形DAC均为直角三角形,设点O为AC的中点,如图2,连接OB,OD,则AO=OC=OB=OD=1,即点O为四面体ABCD外接球的球心,则外接球的半径R=1,
图2
因为二面角DACB的平面角为θ,
且BF⊥AC,DE⊥AC,
拼一个春夏秋冬,博高考无怨无悔!
本节内容结束
同课章节目录
