专题三 立体几何:规范答题——立体几何解答题 课件(共16张PPT)
文档属性
| 名称 | 专题三 立体几何:规范答题——立体几何解答题 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 766.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 21:25:18 | ||
图片预览






文档简介
(共16张PPT)
上篇 专题三 立体几何
规范答题示范课——立体几何解答题
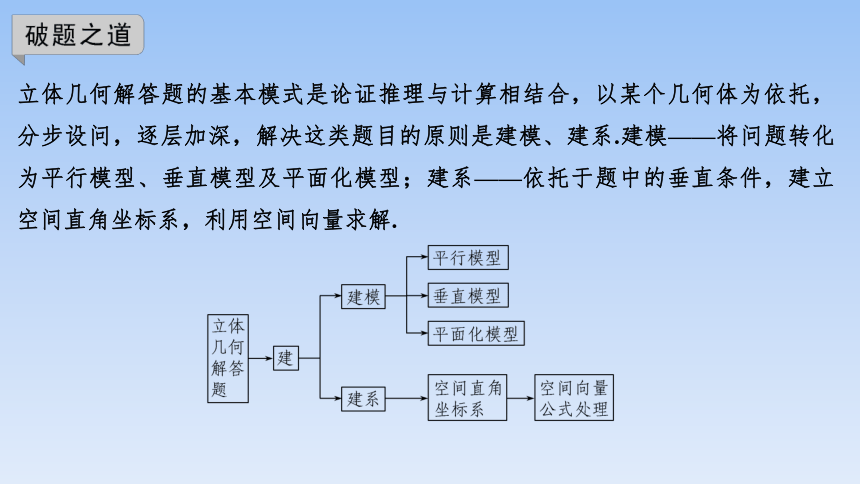
立体几何解答题的基本模式是论证推理与计算相结合,以某个几何体为依托,分步设问,逐层加深,解决这类题目的原则是建模、建系.建模——将问题转化为平行模型、垂直模型及平面化模型;建系——依托于题中的垂直条件,建立空间直角坐标系,利用空间向量求解.
(1)证明:PA⊥平面PBC;
又PA2+PC2=AC2,故PA⊥PC.
又PB,PC 平面PBC,PB∩PC=P,
所以PA⊥平面PBC. 5分
(2)求二面角B-PC-E的余弦值.
由题设可得E(0,1,0),A(0,-1,0),
因为二面角B-PC-E为锐角,
1.(2021·天津卷)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱BC的中点,F为棱CD的中点.
(1)求证:D1F∥平面A1EC1;
证明 以A为原点,AB,AD,AA1分别为x,y,z轴,建立如图空间直角坐标系,
则A(0,0,0),A1(0,0,2),B(2,0,0),C(2,2,0),D(0,2,0),C1(2,2,2),D1(0,2,2).
因为E为棱BC的中点,F为棱CD的中点,所以E(2,1,0),F(1,2,0),
设平面A1EC1的一个法向量为m=(x1,y1,z1),
令x1=2,则y1=-2,z1=1,即m=(2,-2,1).
(2)求直线AC1与平面A1EC1所成角的正弦值;
设直线AC1与平面A1EC1所成角为θ,
(3)求二面角A-A1C1-E的正弦值.
(1)证明:GF∥平面ABC;
∴MN∥CD,且MN=CD,
∴四边形CDNM为平行四边形,∴CM∥DN,
又F为ED的中点,∴GF∥DN,得GF∥CM,
又CM 平面ABC,GF 平面ABC,
∴GF∥平面ABC.
(2)当多面体ABCDE的体积最大时,求二面角ABED的余弦值.
解 在平面ABC内,过B作BH⊥AC,交AC于H,
∵平面ACDE⊥平面ABC,且平面ACDE∩平面ABC=AC,BH 平面ABC.
∴BH⊥平面ACDE,则BH为四棱锥BACDE的高,
又底面ACDE的面积确定,
∴要使多面体ABCDE的体积最大,
∴H为AC的中点,连接HF,易知HB,HC,HF两两垂直.
以H为坐标原点,分别以HB,HC,HF所在直线为x,y,z轴建立如图所示的直角坐标系Hxyz.
则A(0,-1,0),B(1,0,0),
E(0,-1,2),D(0,1,1).
设n1=(x1,y1,z1)为平面ABE的法向量,
取y1=-1,得n1=(1,-1,0).
设n2=(x2,y2,z2)为平面DBE的法向量,
上篇 专题三 立体几何
规范答题示范课——立体几何解答题
立体几何解答题的基本模式是论证推理与计算相结合,以某个几何体为依托,分步设问,逐层加深,解决这类题目的原则是建模、建系.建模——将问题转化为平行模型、垂直模型及平面化模型;建系——依托于题中的垂直条件,建立空间直角坐标系,利用空间向量求解.
(1)证明:PA⊥平面PBC;
又PA2+PC2=AC2,故PA⊥PC.
又PB,PC 平面PBC,PB∩PC=P,
所以PA⊥平面PBC. 5分
(2)求二面角B-PC-E的余弦值.
由题设可得E(0,1,0),A(0,-1,0),
因为二面角B-PC-E为锐角,
1.(2021·天津卷)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱BC的中点,F为棱CD的中点.
(1)求证:D1F∥平面A1EC1;
证明 以A为原点,AB,AD,AA1分别为x,y,z轴,建立如图空间直角坐标系,
则A(0,0,0),A1(0,0,2),B(2,0,0),C(2,2,0),D(0,2,0),C1(2,2,2),D1(0,2,2).
因为E为棱BC的中点,F为棱CD的中点,所以E(2,1,0),F(1,2,0),
设平面A1EC1的一个法向量为m=(x1,y1,z1),
令x1=2,则y1=-2,z1=1,即m=(2,-2,1).
(2)求直线AC1与平面A1EC1所成角的正弦值;
设直线AC1与平面A1EC1所成角为θ,
(3)求二面角A-A1C1-E的正弦值.
(1)证明:GF∥平面ABC;
∴MN∥CD,且MN=CD,
∴四边形CDNM为平行四边形,∴CM∥DN,
又F为ED的中点,∴GF∥DN,得GF∥CM,
又CM 平面ABC,GF 平面ABC,
∴GF∥平面ABC.
(2)当多面体ABCDE的体积最大时,求二面角ABED的余弦值.
解 在平面ABC内,过B作BH⊥AC,交AC于H,
∵平面ACDE⊥平面ABC,且平面ACDE∩平面ABC=AC,BH 平面ABC.
∴BH⊥平面ACDE,则BH为四棱锥BACDE的高,
又底面ACDE的面积确定,
∴要使多面体ABCDE的体积最大,
∴H为AC的中点,连接HF,易知HB,HC,HF两两垂直.
以H为坐标原点,分别以HB,HC,HF所在直线为x,y,z轴建立如图所示的直角坐标系Hxyz.
则A(0,-1,0),B(1,0,0),
E(0,-1,2),D(0,1,1).
设n1=(x1,y1,z1)为平面ABE的法向量,
取y1=-1,得n1=(1,-1,0).
设n2=(x2,y2,z2)为平面DBE的法向量,
同课章节目录
