专题二 数列:规范答题——数列解答题 课件(共12张PPT)
文档属性
| 名称 | 专题二 数列:规范答题——数列解答题 课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 555.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 21:21:55 | ||
图片预览





文档简介
(共12张PPT)
上篇 专题二 数列
规范答题示范课——数列解答题
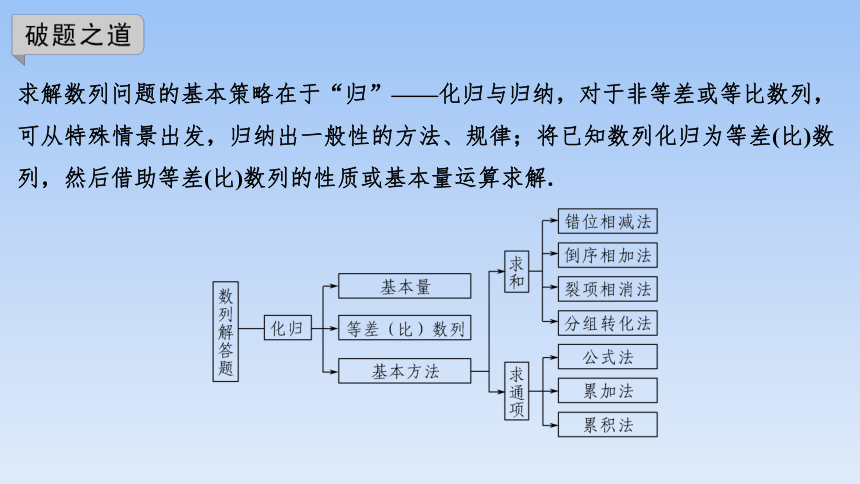
求解数列问题的基本策略在于“归”——化归与归纳,对于非等差或等比数列,可从特殊情景出发,归纳出一般性的方法、规律;将已知数列化归为等差(比)数列,然后借助等差(比)数列的性质或基本量运算求解.
(12分)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
解 设等比数列{an}的公比为q,且q≠1,
依题意,2a1=a2+a3,即2a1=a1q+a1q2. 2分
所以q2+q-2=0,解得q=1(舍去)或q=-2. 4分
故{an}的公比为-2. 5分
(2)若a1=1,求数列{nan}的前n项和.
解 记Sn为{nan}的前n项和.
依题意及(1)知,{an}是首项为1,公比为-2的等比数列,所以an=(-2)n-1,7分
所以Sn=1+2×(-2)+3×(-2)2+…+n·(-2)n-1,
-2Sn=-2+2×(-2)2+…+(n-1)·(-2)n-1+n·(-2)n. 9分
两式相减,得
得步骤分:对于解题过程中踩分点的步骤有则给分,无则没分,如第(1)问中,写出2a1=a2+a3及公比q≠1.
得关键分:数列解答题要严谨,如第(2)问“首先明确指出数列{an}的首项和公比(基本量),求出an=(-2)n-1,再写出Sn=1+2×(-2)+3×(-2)2+…+n·
(-2)n-1.
(1)记bn=a2n,写出b1,b2,并求数列{bn}的通项公式;
所以b1=a2=a1+1=2,
b2=a4=a3+1=a2+2+1=5.
因为bn=a2n,
所以bn+1=a2n+2=a2n+1+1=a2n+1+1=a2n+2+1=a2n+3,
所以bn+1-bn=a2n+3-a2n=3,
所以数列{bn}是以2为首项,3为公差的等差数列,
所以bn=2+3(n-1)=3n-1,n∈N*.
(2)求{an}的前20项和.
所以k∈N*时,a2k=a2k-1+1=a2k-1+1,
即a2k=a2k-1+1,①
a2k+1=a2k+2,②
a2k+2=a2k+1+1=a2k+1+1,即a2k+2=a2k+1+1,③
所以①+②得a2k+1=a2k-1+3,即a2k+1-a2k-1=3,
所以数列{an}的奇数项是以1为首项,3为公差的等差数列;
②+③得a2k+2=a2k+3,即a2k+2-a2k=3,
又a2=2,所以数列{an}的偶数项是以2为首项,3为公差的等差数列.
2.已知数列{an}与{bn}满足:a1+a2+a3+…+an=2bn(n∈N*),若{an}是各项为正数的等比数列,且a1=2,b3=b2+4.
(1)求数列{an}与{bn}的通项公式;
解 由题意知,a1+a2+a3+…+an=2bn,①
当n≥2时,a1+a2+a3+…+an-1=2bn-1,②
①-②可得an=2(bn-bn-1)
a3=2(b3-b2)=2×4=8,
∵a1=2,an>0,设{an}的公比为q,
∴a1q2=8 q=2,
∴an=2×2n-1=2n(n∈N*).
∴bn=2n-1(n∈N*).
上篇 专题二 数列
规范答题示范课——数列解答题
求解数列问题的基本策略在于“归”——化归与归纳,对于非等差或等比数列,可从特殊情景出发,归纳出一般性的方法、规律;将已知数列化归为等差(比)数列,然后借助等差(比)数列的性质或基本量运算求解.
(12分)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
解 设等比数列{an}的公比为q,且q≠1,
依题意,2a1=a2+a3,即2a1=a1q+a1q2. 2分
所以q2+q-2=0,解得q=1(舍去)或q=-2. 4分
故{an}的公比为-2. 5分
(2)若a1=1,求数列{nan}的前n项和.
解 记Sn为{nan}的前n项和.
依题意及(1)知,{an}是首项为1,公比为-2的等比数列,所以an=(-2)n-1,7分
所以Sn=1+2×(-2)+3×(-2)2+…+n·(-2)n-1,
-2Sn=-2+2×(-2)2+…+(n-1)·(-2)n-1+n·(-2)n. 9分
两式相减,得
得步骤分:对于解题过程中踩分点的步骤有则给分,无则没分,如第(1)问中,写出2a1=a2+a3及公比q≠1.
得关键分:数列解答题要严谨,如第(2)问“首先明确指出数列{an}的首项和公比(基本量),求出an=(-2)n-1,再写出Sn=1+2×(-2)+3×(-2)2+…+n·
(-2)n-1.
(1)记bn=a2n,写出b1,b2,并求数列{bn}的通项公式;
所以b1=a2=a1+1=2,
b2=a4=a3+1=a2+2+1=5.
因为bn=a2n,
所以bn+1=a2n+2=a2n+1+1=a2n+1+1=a2n+2+1=a2n+3,
所以bn+1-bn=a2n+3-a2n=3,
所以数列{bn}是以2为首项,3为公差的等差数列,
所以bn=2+3(n-1)=3n-1,n∈N*.
(2)求{an}的前20项和.
所以k∈N*时,a2k=a2k-1+1=a2k-1+1,
即a2k=a2k-1+1,①
a2k+1=a2k+2,②
a2k+2=a2k+1+1=a2k+1+1,即a2k+2=a2k+1+1,③
所以①+②得a2k+1=a2k-1+3,即a2k+1-a2k-1=3,
所以数列{an}的奇数项是以1为首项,3为公差的等差数列;
②+③得a2k+2=a2k+3,即a2k+2-a2k=3,
又a2=2,所以数列{an}的偶数项是以2为首项,3为公差的等差数列.
2.已知数列{an}与{bn}满足:a1+a2+a3+…+an=2bn(n∈N*),若{an}是各项为正数的等比数列,且a1=2,b3=b2+4.
(1)求数列{an}与{bn}的通项公式;
解 由题意知,a1+a2+a3+…+an=2bn,①
当n≥2时,a1+a2+a3+…+an-1=2bn-1,②
①-②可得an=2(bn-bn-1)
a3=2(b3-b2)=2×4=8,
∵a1=2,an>0,设{an}的公比为q,
∴a1q2=8 q=2,
∴an=2×2n-1=2n(n∈N*).
∴bn=2n-1(n∈N*).
同课章节目录
