专题三 立体几何:第3讲 立体几何中的向量方法 课件(共90张PPT)
文档属性
| 名称 | 专题三 立体几何:第3讲 立体几何中的向量方法 课件(共90张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 21:19:52 | ||
图片预览





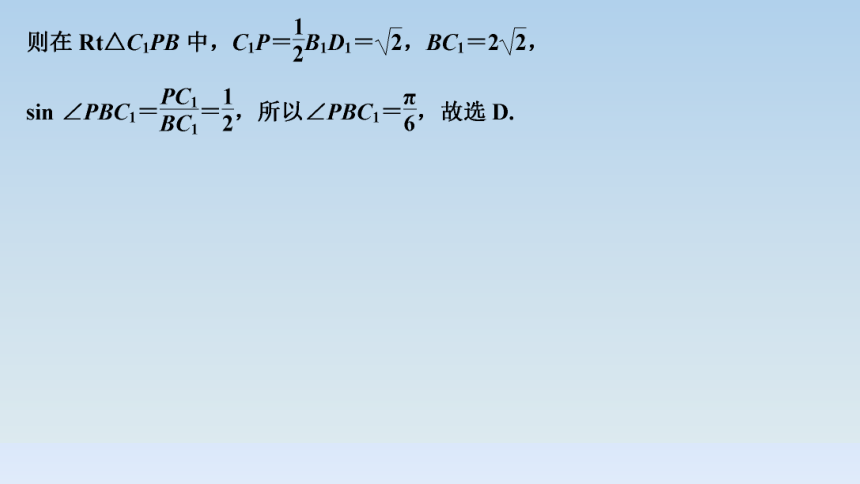




文档简介
(共90张PPT)
上篇 专题三 立体几何
第3讲 立体几何中的向量方法
高考定位
以空间几何体为载体考查空间角是高考命题的重点,常与空间线面关系的证明相结合,热点为二面角的求解,均以解答题的形式进行考查,难度主要体现在建立空间直角坐标系和准确计算上.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
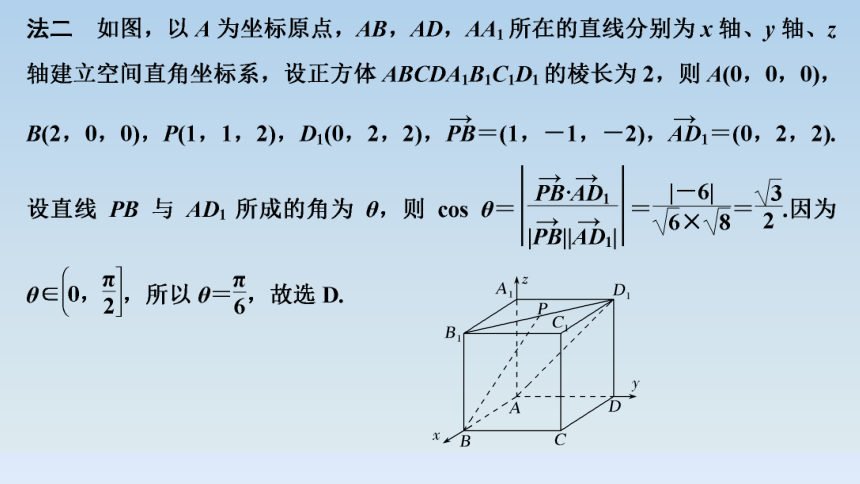
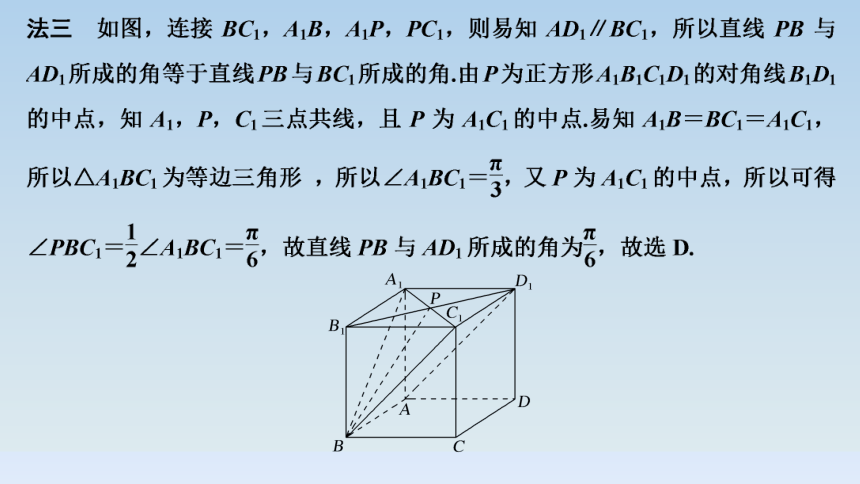
1.(2021·全国乙卷)在正方体ABCDA1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )
D
解析 法一 如图,连接C1P,因为ABCDA1B1C1D1是正方体,且P为B1D1的中点,所以C1P⊥B1D1,又C1P⊥BB1,B1D1∩BB1=B1,B1D1,BB1 平面B1BP,所以C1P⊥平面B1BP.又BP 平面B1BP,所以有C1P⊥BP.连接BC1,则AD1∥BC1,所以∠PBC1为直线PB与AD1所成的角.设正方体ABCDA1B1C1D1的棱长为2,
(1)证明:AB⊥PM;
证明 因为底面ABCD是平行四边形,
∠ABC=120°,BC=4,AB=1,且M为BC的中点,
所以CM=2,CD=1,∠DCM=60°,易得CD⊥DM.
又PD⊥DC,且PD∩DM=D,PD,DM 平面PDM,
所以CD⊥平面PDM.
因为AB∥CD,所以AB⊥平面PDM.
又PM 平面PDM,所以AB⊥PM.
(2)求直线AN与平面PDM所成角的正弦值.
解 法一 由(1)知AB⊥平面PDM,
所以∠NAB为直线AN与平面PDM所成角的余角.
连接AM,因为PM⊥MD,由(1)知PM⊥DC,
又MD,DC 平面ABCD,MD∩DC=D,
所以PM⊥平面ABCD,又AM 平面ABCD,
所以PM⊥AM.
因为∠ABC=120°,AB=1,
BM=2,
法二 因为PM⊥MD,由(1)知PM⊥DC,又MD,DC 平面ABCD,MD∩DC=D,
所以PM⊥平面ABCD.
连接AM,则PM⊥AM.
因为∠ABC=120°,AB=1,
BM=2,
由(1)知CD⊥DM,
过点M作ME∥CD交AD于点E,则ME⊥MD.
故可以以M为坐标原点,MD,ME,MP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
设直线AN与平面PDM所成的角为θ,
(1)证明:平面QAD⊥平面ABCD;
证明 取AD的中点为O,连接QO,CO.
因为QA=QD,OA=OD,则QO⊥AD,
因为QC=3,故QC2=QO2+OC2,故△QOC为直角三角形且QO⊥OC.
因为OC∩AD=O,OC,AD 平面ABCD,故QO⊥平面ABCD.
因为QO 平面QAD,故平面QAD⊥平面ABCD.
(2)求二面角B-QD-A的平面角的余弦值.
解 在平面ABCD内,过O作OT∥CD,交BC于T,则OT⊥AD,结合(1)中的QO⊥平面ABCD,故可建如图所示的空间坐标系,
易知平面QAD的一个法向量为m=(1,0,0),
1.直线与平面、平面与平面的平行与垂直的向量方法
设直线l的方向向量为a=(a1,b1,c1),平面α,β的法向量分别为μ=(a2,b2,c2),v=(a3,b3,c3),则
(1)线面平行
l∥α a⊥μ a·μ=0 a1a2+b1b2+c1c2=0.
(2)线面垂直
l⊥α a∥μ a=kμ a1=ka2,b1=kb2,c1=kc2.
(3)面面平行
α∥β μ∥v μ=λv a2=λa3,b2=λb3,c2=λc3.
(4)面面垂直
α⊥β μ⊥v μ·v=0 a2a3+b2b3+c2c3=0.
2.直线与直线、直线与平面、平面与平面所成的角计算
设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2),平面α,β的法向量分别为μ=(a3,b3,c3),v=(a4,b4,c4)(以下相同).
(1)线线角
2
热点聚焦 分类突破
热点一 利用空间向量证明平行、垂直
【例1】 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
证明 依题意,以点A为原点建立空间直角坐标系(如图),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得E(1,1,1).
(2)BE∥平面PAD;
证明 因为AB⊥AD,又PA⊥平面ABCD,AB 平面ABCD,
所以AB⊥PA,PA∩AD=A,PA,AD 平面PAD,
所以AB⊥平面PAD,
又BE 平面PAD,
所以BE∥平面PAD.
(3)平面PCD⊥平面PAD.
设平面PCD的法向量为n=(x,y,z),
1.利用向量法证明平行、垂直,关键是建立恰当的坐标系(尽可能利用垂直条件,准确写出相关点的坐标,进而用向量表示涉及到直线、平面的要素).
2.向量证明的核心是利用向量的数量积或数乘向量,但向量证明仍然离不开立体几何的定理,如在(2)中忽略BE 平面PAD而致误.
探究提高
(1)求证:BD⊥PC.
设PD=a,则P(0,0,a),
热点二 利用向量求线线角、线面角
【例2】 (2021·上海卷改编)如图,在四棱锥PABCD中,底面ABCD为正方形,边长为4,E为AB的中点,PE⊥平面ABCD.
(1)若△PAB为等边三角形,求四棱锥P-ABCD的体积;
解 ∵正方形ABCD的边长为4,且△PAB为等边三角形,E为AB的中点,
又PE⊥平面ABCD,
(2)若CD的中点为F,PF与平面ABCD所成角为45°,求PC与AD所成角的余弦值.
解 如图,连接EF,
∵PE⊥平面ABCD,
EF,AB 平面ABCD,
∴PE⊥EF,PE⊥AB,
又四边形ABCD为正方形,
E,F分别为AB,CD的中点,
∴EF⊥AB,
∴AB,EF,PE两两垂直.
以E为坐标原点,EB,EF,EP所在直线分别为x,y,z轴建立空间直角坐标系,则C(2,4,0),A(-2,0,0),D(-2,4,0),
∵PF与平面ABCD所成角为45°,∴∠PFE=45°,
∴PE=EF·tan ∠PFE=4,∴P(0,0,4),
设PC与AD所成的角为θ,则
1.异面直线所成的角θ,可以通过两直线的方向向量的夹角φ求得,即cos θ=|cos φ|.
2.直线与平面所成的角θ主要通过直线的方向向量与平面的法向量的夹角φ求得,即sin θ=|cos φ|,有时也可分别求出斜线与它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角).
探究提高
【训练2】 (2021·宿迁质检)在直角梯形ABCD中,∠ABC=90°,BC∥AD,AD=4,AB=BC=2,M为线段AD中点.将△ABC沿AC折起,使平面ABC⊥平面ACD,得到几何体BACD.
(1)求证:AB⊥平面BCD;
证明 在直角梯形ABCD中,∠ABC=90°,AB=BC=2,AD=4,
因此在△ACD中,AD2=CD2+AC2,从而CD⊥AC.
又∵平面ABC⊥平面ACD,且平面ABC∩平面ACD=AC,CD 平面ACD,
∴CD⊥平面ABC,又AB 平面ABC,∴CD⊥AB.
又AB⊥BC,且BC∩CD=C,∴AB⊥平面BCD.
(2)求直线BD与平面BCM所成角的正弦值.
解 取AC的中点O,连接OB,由题设可知△ABC为等腰直角三角形,
∴OB⊥平面ACM.
连接OM,∵M,O分别为AD和AC的中点,
∴OM∥CD.
由(1)可知OM⊥AC,
故以OM,OC,OB所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.
则求得平面BCM的一个法向量n=(1,1,1).
设直线BD与平面BCM所成的角为θ,
热点三 利用向量求二面角
(1)求证:GF∥平面PDC;
证明 取PD的中点E,连接AE,CE.
解 设O为AD的中点,因为△PAD为正三角形,则PO⊥AD,
又因平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,PO 平面PAD,
所以PO⊥平面ABCD.
设平面PBC的法向量为n=(x,y,z),
1.二面角的大小可以利用分别在两个半平面内与棱垂直的直线的方向向量的夹角(或其补角)或通过二面角的两个面的法向量的夹角求得,它等于两个法向量的夹角或其补角.
2.利用向量法求二面角,必须能判定“所求二面角的平面角是锐角或钝角”,否则解法是不严谨的.
探究提高
【训练3】 (2021·马鞍山质检)如图,已知三棱锥SABC中,△ABC是边长为2的等边三角形,且SB=SC=4,点D为SC的中点,DA=2.
(1)求证:平面SAB⊥平面ABC;
证明 因为SC=4,且点D为SC的中点,
所以SD=DC=2.
又AC=DA=2,
从而SC2=SA2+AC2,则SA⊥AC.
又△SAB≌△SAC,得SA⊥AB,
又AB∩AC=A,AB,AC 平面ABC,所以SA⊥平面ABC,
又SA 平面SAB,所以平面SAB⊥平面ABC.
(2)求二面角S-AB-D的正弦值.
解 以A为坐标原点,AB所在直线为x轴,在平面ABC内过点A垂直于AB的直线为y轴,AS所在直线为z轴,建立如图所示空间直角坐标系.
令z=1,得m=(0,-2,1).
又平面SAB的一个法向量n=(0,1,0),
热点四 利用空间向量求解探索性问题
【例4】 (2021·青岛诊断)如图,在四棱锥PABCD中,底面ABCD为菱形,∠ABC=60°,AB=PA=2,PA⊥平面ABCD,E,M分别是BC,PD的中点,点F在棱PC上移动.
(1)证明:无论点F在PC上如何移动,都有平面AEF⊥平面PAD;
证明 如图所示,连接AC.
∵底面ABCD为菱形,∠ABC=60°,
∴△ABC为正三角形,
∵E是BC的中点,∴AE⊥BC.
又AD∥BC,∴AE⊥AD.
∵PA⊥平面ABCD,AE 平面ABCD,∴PA⊥AE,
∵PA∩AD=A,PA,AD在平面PAD内,
∴AE⊥平面PAD.
∵AE 平面AEF,∴平面AEF⊥平面PAD.
(2)是否存在点F,使得直线AF与平面PCD所成的角最大,若存在,试确定点F的位置.
故存在点F,使得直线AF与平面PCD所成的角最大,此时F为PC的中点.
1.空间向量法最适合于解决立体几何中的探索性问题,它无需进行复杂的作图、论证、推理,只需通过坐标运算进行判断.但注意空间坐标系建立的规范性及计算的准确性,否则容易出现错误.
2.利用空间向量求解探索性问题:(1)假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论;(2)在这个前提下进行逻辑推理,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标(或参数)是否有解,是否有规定范围内的解”等.若由此推导出矛盾,则否定假设;否则,给出肯定结论.
探究提高
(1)求证:AC⊥SD;
证明 连接BD交AC于点O,连接SO,由题意知SO⊥AC.
在正方形ABCD中,AC⊥BD.
因为BD∩SO=O,BD,SO 平面SBD,
所以AC⊥平面SBD,又SD 平面SBD,所以AC⊥SD.
(2)若SD⊥平面PAC,求二面角P-AC-S的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SC∶SE的值;若不存在,试说明理由.
解 在棱SC上存在一点E使BE∥平面PAC.理由如下:
专题训练 对接高考
3
巩固提升
一、选择题
1.在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成角的正弦值为( )
B
设平面A1ED的法向量为n1=(1,y,z),
∴n1=(1,2,2).
∵平面ABCD的法向量为n2=(0,0,1),
2.如图,在四棱锥SABCD中,SD⊥平面ABCD,AB∥CD,AD⊥CD,SD=CD,AB=AD,CD=2AD,M是BC中点,N是线段SA上的点,设MN与平面SAD所成角为α,则sin α的最大值为( )
A
3.(多选)如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1,G为线段EC上的动点,下列结论正确的是( )
ABC
A.EC⊥AF
B.该几何体外接球的表面积为3π
C.若G为线段EC的中点,则GB∥平面AEF
D.AG2+BG2的最小值为3
所以AE⊥ED,即AE,DE,EF两两垂直,所以建立如图所示的空间直角坐标系,
设AB=EF=CD=2,
则E(0,0,0),A(1,0,0),F(0,2,0),C(0,2,1),
5.(2021·兰州诊断)如图所示,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB的中点,则点E到平面ACD1的距离为________.
解析 如图,以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,
则D1(0,0,1),E(1,1,0),A(1,0,0),C(0,2,0).
设平面ACD1的法向量为n=(a,b,c),
∴点E到平面ACD1的距离
三、解答题
6.如图,已知三棱柱ABCA1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.
(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;
证明 因为侧面BB1C1C是矩形且M,N分别为BC,B1C1的中点,所以MN∥CC1.
又由已知得AA1∥CC1,故AA1∥MN.
因为△A1B1C1是正三角形,所以B1C1⊥A1N.
又侧面BB1C1C是矩形,所以B1C1⊥MN.
又A1N∩MN=N,A1N,MN 平面A1AMN,
所以B1C1⊥平面A1AMN.又B1C1 平面EB1C1F,
所以平面A1AMN⊥平面EB1C1F.
(2)设O为△A1B1C1的中心.若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.
连接NP,AO∥平面EB1C1F,AO 平面A1AMN,
平面A1AMN∩平面EB1C1F=PN,故AO∥PN.
又AP∥ON,则四边形AONP为平行四边形,
由(1)知平面A1AMN⊥平面ABC.
作NQ⊥AM,垂足为Q,则NQ⊥平面ABC.
设Q(a,0,0),则
又n=(0,-1,0)是平面A1AMN的一个法向量,
7.(2021·全国乙卷)如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.
(1)求BC;
解 连接BD交AM于点E,
因为PD⊥底面ABCD,AM 平面ABCD,所以PD⊥AM,
又因为PB⊥AM,PB∩PD=P,PB,PD 平面PBD,
所以AM⊥平面PBD,
因为BD 平面PBD,所以AM⊥BD.
设BC=x,因为M为BC的中点,
因为AB⊥AD,AM⊥BD,所以△DAB∽△ABM,
(2)求二面角A-PM-B的正弦值.
解 由题意DA,DC,DP两两互相垂直,以D为原点,DA为x轴,DC为y轴,DP为z轴建立如图空间直角坐标系.
设平面BPM的法向量n=(x2,y2,z2),
8.(2021·新高考Ⅰ卷)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.
(1)证明:OA⊥CD;
证明 因为AB=AD,O为BD的中点,所以OA⊥BD,
又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,
AO 平面ABD,所以AO⊥平面BCD,
又CD 平面BCD,所以AO⊥CD.
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角EBCD的大小为45°,求三棱锥A-BCD的体积.
解 如图所示,以O为坐标原点,OB,OA所在直线分别为x,z轴,在平面BCD内,以过点O且与BD垂直的直线为y轴建立空间直角坐标系.
因为△OCD是边长为1的正三角形,且O为BD的中点,
所以OC=OB=OD=1,
由题意可知平面BCD的一个法向量为n=(0,0,1).
设平面BCE的法向量为m=(x,y,z),
因为二面角E-BC-D的大小为45°,
得a=1,即OA=1.由(1)得OA⊥平面BCD,
9.(2021·全国甲卷)已知直三棱柱ABCA1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
能力突破
(1)证明:BF⊥DE;
证明 因为E,F分别是AC和CC1的中点,且AB=BC=2,侧面AA1B1B为正方形,
∵三棱柱ABCA1B1C1为直三棱柱,
∴BB1⊥AB且BB1⊥BC,
则BA,BC,BB1两两互相垂直,
故以B为坐标原点,以BA,BC,BB1所在直线分别为x,y,z轴建立空间直角坐标系B-xyz,
(2)当B1D为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?
解 易知平面BB1C1C的一个法向量为n1=(1,0,0).
设平面DFE的法向量为n2=(x,y,z),
令x=3,得y=m+1,z=2-m,
于是,平面DFE的一个法向量为n2=(3,m+1,2-m),
设平面BB1C1C与平面DFE所成的二面角为θ,
(1)求证:平面PBD⊥平面PBC;
所以CD2=BD2+BC2,故BC⊥BD.
又BC⊥PD,PD∩BD=D,且BD,PD 平面PBD,所以BC⊥平面PBD.
因为BC 平面PBC,所以平面PBC⊥平面PBD.
解 设E为BD的中点,连接PE.
由(1)得BC⊥平面PBD,又BC 平面ABCD,所以平面ABCD⊥平面PBD.
又平面ABCD∩平面PBD=BD,PE 平面PBD,
所以PE⊥平面ABCD.
则A(0,0,0),B(0,2,0),C(2,4,0),D(2,0,0),P(1,1,2).
所以M(2-λ,4-3λ,2λ).
取x=2λ,得平面ABM的一个法向量n=(2λ,0,λ-2).
上篇 专题三 立体几何
第3讲 立体几何中的向量方法
高考定位
以空间几何体为载体考查空间角是高考命题的重点,常与空间线面关系的证明相结合,热点为二面角的求解,均以解答题的形式进行考查,难度主要体现在建立空间直角坐标系和准确计算上.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
1.(2021·全国乙卷)在正方体ABCDA1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )
D
解析 法一 如图,连接C1P,因为ABCDA1B1C1D1是正方体,且P为B1D1的中点,所以C1P⊥B1D1,又C1P⊥BB1,B1D1∩BB1=B1,B1D1,BB1 平面B1BP,所以C1P⊥平面B1BP.又BP 平面B1BP,所以有C1P⊥BP.连接BC1,则AD1∥BC1,所以∠PBC1为直线PB与AD1所成的角.设正方体ABCDA1B1C1D1的棱长为2,
(1)证明:AB⊥PM;
证明 因为底面ABCD是平行四边形,
∠ABC=120°,BC=4,AB=1,且M为BC的中点,
所以CM=2,CD=1,∠DCM=60°,易得CD⊥DM.
又PD⊥DC,且PD∩DM=D,PD,DM 平面PDM,
所以CD⊥平面PDM.
因为AB∥CD,所以AB⊥平面PDM.
又PM 平面PDM,所以AB⊥PM.
(2)求直线AN与平面PDM所成角的正弦值.
解 法一 由(1)知AB⊥平面PDM,
所以∠NAB为直线AN与平面PDM所成角的余角.
连接AM,因为PM⊥MD,由(1)知PM⊥DC,
又MD,DC 平面ABCD,MD∩DC=D,
所以PM⊥平面ABCD,又AM 平面ABCD,
所以PM⊥AM.
因为∠ABC=120°,AB=1,
BM=2,
法二 因为PM⊥MD,由(1)知PM⊥DC,又MD,DC 平面ABCD,MD∩DC=D,
所以PM⊥平面ABCD.
连接AM,则PM⊥AM.
因为∠ABC=120°,AB=1,
BM=2,
由(1)知CD⊥DM,
过点M作ME∥CD交AD于点E,则ME⊥MD.
故可以以M为坐标原点,MD,ME,MP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
设直线AN与平面PDM所成的角为θ,
(1)证明:平面QAD⊥平面ABCD;
证明 取AD的中点为O,连接QO,CO.
因为QA=QD,OA=OD,则QO⊥AD,
因为QC=3,故QC2=QO2+OC2,故△QOC为直角三角形且QO⊥OC.
因为OC∩AD=O,OC,AD 平面ABCD,故QO⊥平面ABCD.
因为QO 平面QAD,故平面QAD⊥平面ABCD.
(2)求二面角B-QD-A的平面角的余弦值.
解 在平面ABCD内,过O作OT∥CD,交BC于T,则OT⊥AD,结合(1)中的QO⊥平面ABCD,故可建如图所示的空间坐标系,
易知平面QAD的一个法向量为m=(1,0,0),
1.直线与平面、平面与平面的平行与垂直的向量方法
设直线l的方向向量为a=(a1,b1,c1),平面α,β的法向量分别为μ=(a2,b2,c2),v=(a3,b3,c3),则
(1)线面平行
l∥α a⊥μ a·μ=0 a1a2+b1b2+c1c2=0.
(2)线面垂直
l⊥α a∥μ a=kμ a1=ka2,b1=kb2,c1=kc2.
(3)面面平行
α∥β μ∥v μ=λv a2=λa3,b2=λb3,c2=λc3.
(4)面面垂直
α⊥β μ⊥v μ·v=0 a2a3+b2b3+c2c3=0.
2.直线与直线、直线与平面、平面与平面所成的角计算
设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2),平面α,β的法向量分别为μ=(a3,b3,c3),v=(a4,b4,c4)(以下相同).
(1)线线角
2
热点聚焦 分类突破
热点一 利用空间向量证明平行、垂直
【例1】 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
证明 依题意,以点A为原点建立空间直角坐标系(如图),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得E(1,1,1).
(2)BE∥平面PAD;
证明 因为AB⊥AD,又PA⊥平面ABCD,AB 平面ABCD,
所以AB⊥PA,PA∩AD=A,PA,AD 平面PAD,
所以AB⊥平面PAD,
又BE 平面PAD,
所以BE∥平面PAD.
(3)平面PCD⊥平面PAD.
设平面PCD的法向量为n=(x,y,z),
1.利用向量法证明平行、垂直,关键是建立恰当的坐标系(尽可能利用垂直条件,准确写出相关点的坐标,进而用向量表示涉及到直线、平面的要素).
2.向量证明的核心是利用向量的数量积或数乘向量,但向量证明仍然离不开立体几何的定理,如在(2)中忽略BE 平面PAD而致误.
探究提高
(1)求证:BD⊥PC.
设PD=a,则P(0,0,a),
热点二 利用向量求线线角、线面角
【例2】 (2021·上海卷改编)如图,在四棱锥PABCD中,底面ABCD为正方形,边长为4,E为AB的中点,PE⊥平面ABCD.
(1)若△PAB为等边三角形,求四棱锥P-ABCD的体积;
解 ∵正方形ABCD的边长为4,且△PAB为等边三角形,E为AB的中点,
又PE⊥平面ABCD,
(2)若CD的中点为F,PF与平面ABCD所成角为45°,求PC与AD所成角的余弦值.
解 如图,连接EF,
∵PE⊥平面ABCD,
EF,AB 平面ABCD,
∴PE⊥EF,PE⊥AB,
又四边形ABCD为正方形,
E,F分别为AB,CD的中点,
∴EF⊥AB,
∴AB,EF,PE两两垂直.
以E为坐标原点,EB,EF,EP所在直线分别为x,y,z轴建立空间直角坐标系,则C(2,4,0),A(-2,0,0),D(-2,4,0),
∵PF与平面ABCD所成角为45°,∴∠PFE=45°,
∴PE=EF·tan ∠PFE=4,∴P(0,0,4),
设PC与AD所成的角为θ,则
1.异面直线所成的角θ,可以通过两直线的方向向量的夹角φ求得,即cos θ=|cos φ|.
2.直线与平面所成的角θ主要通过直线的方向向量与平面的法向量的夹角φ求得,即sin θ=|cos φ|,有时也可分别求出斜线与它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角).
探究提高
【训练2】 (2021·宿迁质检)在直角梯形ABCD中,∠ABC=90°,BC∥AD,AD=4,AB=BC=2,M为线段AD中点.将△ABC沿AC折起,使平面ABC⊥平面ACD,得到几何体BACD.
(1)求证:AB⊥平面BCD;
证明 在直角梯形ABCD中,∠ABC=90°,AB=BC=2,AD=4,
因此在△ACD中,AD2=CD2+AC2,从而CD⊥AC.
又∵平面ABC⊥平面ACD,且平面ABC∩平面ACD=AC,CD 平面ACD,
∴CD⊥平面ABC,又AB 平面ABC,∴CD⊥AB.
又AB⊥BC,且BC∩CD=C,∴AB⊥平面BCD.
(2)求直线BD与平面BCM所成角的正弦值.
解 取AC的中点O,连接OB,由题设可知△ABC为等腰直角三角形,
∴OB⊥平面ACM.
连接OM,∵M,O分别为AD和AC的中点,
∴OM∥CD.
由(1)可知OM⊥AC,
故以OM,OC,OB所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.
则求得平面BCM的一个法向量n=(1,1,1).
设直线BD与平面BCM所成的角为θ,
热点三 利用向量求二面角
(1)求证:GF∥平面PDC;
证明 取PD的中点E,连接AE,CE.
解 设O为AD的中点,因为△PAD为正三角形,则PO⊥AD,
又因平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,PO 平面PAD,
所以PO⊥平面ABCD.
设平面PBC的法向量为n=(x,y,z),
1.二面角的大小可以利用分别在两个半平面内与棱垂直的直线的方向向量的夹角(或其补角)或通过二面角的两个面的法向量的夹角求得,它等于两个法向量的夹角或其补角.
2.利用向量法求二面角,必须能判定“所求二面角的平面角是锐角或钝角”,否则解法是不严谨的.
探究提高
【训练3】 (2021·马鞍山质检)如图,已知三棱锥SABC中,△ABC是边长为2的等边三角形,且SB=SC=4,点D为SC的中点,DA=2.
(1)求证:平面SAB⊥平面ABC;
证明 因为SC=4,且点D为SC的中点,
所以SD=DC=2.
又AC=DA=2,
从而SC2=SA2+AC2,则SA⊥AC.
又△SAB≌△SAC,得SA⊥AB,
又AB∩AC=A,AB,AC 平面ABC,所以SA⊥平面ABC,
又SA 平面SAB,所以平面SAB⊥平面ABC.
(2)求二面角S-AB-D的正弦值.
解 以A为坐标原点,AB所在直线为x轴,在平面ABC内过点A垂直于AB的直线为y轴,AS所在直线为z轴,建立如图所示空间直角坐标系.
令z=1,得m=(0,-2,1).
又平面SAB的一个法向量n=(0,1,0),
热点四 利用空间向量求解探索性问题
【例4】 (2021·青岛诊断)如图,在四棱锥PABCD中,底面ABCD为菱形,∠ABC=60°,AB=PA=2,PA⊥平面ABCD,E,M分别是BC,PD的中点,点F在棱PC上移动.
(1)证明:无论点F在PC上如何移动,都有平面AEF⊥平面PAD;
证明 如图所示,连接AC.
∵底面ABCD为菱形,∠ABC=60°,
∴△ABC为正三角形,
∵E是BC的中点,∴AE⊥BC.
又AD∥BC,∴AE⊥AD.
∵PA⊥平面ABCD,AE 平面ABCD,∴PA⊥AE,
∵PA∩AD=A,PA,AD在平面PAD内,
∴AE⊥平面PAD.
∵AE 平面AEF,∴平面AEF⊥平面PAD.
(2)是否存在点F,使得直线AF与平面PCD所成的角最大,若存在,试确定点F的位置.
故存在点F,使得直线AF与平面PCD所成的角最大,此时F为PC的中点.
1.空间向量法最适合于解决立体几何中的探索性问题,它无需进行复杂的作图、论证、推理,只需通过坐标运算进行判断.但注意空间坐标系建立的规范性及计算的准确性,否则容易出现错误.
2.利用空间向量求解探索性问题:(1)假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论;(2)在这个前提下进行逻辑推理,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标(或参数)是否有解,是否有规定范围内的解”等.若由此推导出矛盾,则否定假设;否则,给出肯定结论.
探究提高
(1)求证:AC⊥SD;
证明 连接BD交AC于点O,连接SO,由题意知SO⊥AC.
在正方形ABCD中,AC⊥BD.
因为BD∩SO=O,BD,SO 平面SBD,
所以AC⊥平面SBD,又SD 平面SBD,所以AC⊥SD.
(2)若SD⊥平面PAC,求二面角P-AC-S的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SC∶SE的值;若不存在,试说明理由.
解 在棱SC上存在一点E使BE∥平面PAC.理由如下:
专题训练 对接高考
3
巩固提升
一、选择题
1.在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成角的正弦值为( )
B
设平面A1ED的法向量为n1=(1,y,z),
∴n1=(1,2,2).
∵平面ABCD的法向量为n2=(0,0,1),
2.如图,在四棱锥SABCD中,SD⊥平面ABCD,AB∥CD,AD⊥CD,SD=CD,AB=AD,CD=2AD,M是BC中点,N是线段SA上的点,设MN与平面SAD所成角为α,则sin α的最大值为( )
A
3.(多选)如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1,G为线段EC上的动点,下列结论正确的是( )
ABC
A.EC⊥AF
B.该几何体外接球的表面积为3π
C.若G为线段EC的中点,则GB∥平面AEF
D.AG2+BG2的最小值为3
所以AE⊥ED,即AE,DE,EF两两垂直,所以建立如图所示的空间直角坐标系,
设AB=EF=CD=2,
则E(0,0,0),A(1,0,0),F(0,2,0),C(0,2,1),
5.(2021·兰州诊断)如图所示,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB的中点,则点E到平面ACD1的距离为________.
解析 如图,以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,
则D1(0,0,1),E(1,1,0),A(1,0,0),C(0,2,0).
设平面ACD1的法向量为n=(a,b,c),
∴点E到平面ACD1的距离
三、解答题
6.如图,已知三棱柱ABCA1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.
(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;
证明 因为侧面BB1C1C是矩形且M,N分别为BC,B1C1的中点,所以MN∥CC1.
又由已知得AA1∥CC1,故AA1∥MN.
因为△A1B1C1是正三角形,所以B1C1⊥A1N.
又侧面BB1C1C是矩形,所以B1C1⊥MN.
又A1N∩MN=N,A1N,MN 平面A1AMN,
所以B1C1⊥平面A1AMN.又B1C1 平面EB1C1F,
所以平面A1AMN⊥平面EB1C1F.
(2)设O为△A1B1C1的中心.若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.
连接NP,AO∥平面EB1C1F,AO 平面A1AMN,
平面A1AMN∩平面EB1C1F=PN,故AO∥PN.
又AP∥ON,则四边形AONP为平行四边形,
由(1)知平面A1AMN⊥平面ABC.
作NQ⊥AM,垂足为Q,则NQ⊥平面ABC.
设Q(a,0,0),则
又n=(0,-1,0)是平面A1AMN的一个法向量,
7.(2021·全国乙卷)如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.
(1)求BC;
解 连接BD交AM于点E,
因为PD⊥底面ABCD,AM 平面ABCD,所以PD⊥AM,
又因为PB⊥AM,PB∩PD=P,PB,PD 平面PBD,
所以AM⊥平面PBD,
因为BD 平面PBD,所以AM⊥BD.
设BC=x,因为M为BC的中点,
因为AB⊥AD,AM⊥BD,所以△DAB∽△ABM,
(2)求二面角A-PM-B的正弦值.
解 由题意DA,DC,DP两两互相垂直,以D为原点,DA为x轴,DC为y轴,DP为z轴建立如图空间直角坐标系.
设平面BPM的法向量n=(x2,y2,z2),
8.(2021·新高考Ⅰ卷)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.
(1)证明:OA⊥CD;
证明 因为AB=AD,O为BD的中点,所以OA⊥BD,
又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,
AO 平面ABD,所以AO⊥平面BCD,
又CD 平面BCD,所以AO⊥CD.
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角EBCD的大小为45°,求三棱锥A-BCD的体积.
解 如图所示,以O为坐标原点,OB,OA所在直线分别为x,z轴,在平面BCD内,以过点O且与BD垂直的直线为y轴建立空间直角坐标系.
因为△OCD是边长为1的正三角形,且O为BD的中点,
所以OC=OB=OD=1,
由题意可知平面BCD的一个法向量为n=(0,0,1).
设平面BCE的法向量为m=(x,y,z),
因为二面角E-BC-D的大小为45°,
得a=1,即OA=1.由(1)得OA⊥平面BCD,
9.(2021·全国甲卷)已知直三棱柱ABCA1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
能力突破
(1)证明:BF⊥DE;
证明 因为E,F分别是AC和CC1的中点,且AB=BC=2,侧面AA1B1B为正方形,
∵三棱柱ABCA1B1C1为直三棱柱,
∴BB1⊥AB且BB1⊥BC,
则BA,BC,BB1两两互相垂直,
故以B为坐标原点,以BA,BC,BB1所在直线分别为x,y,z轴建立空间直角坐标系B-xyz,
(2)当B1D为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?
解 易知平面BB1C1C的一个法向量为n1=(1,0,0).
设平面DFE的法向量为n2=(x,y,z),
令x=3,得y=m+1,z=2-m,
于是,平面DFE的一个法向量为n2=(3,m+1,2-m),
设平面BB1C1C与平面DFE所成的二面角为θ,
(1)求证:平面PBD⊥平面PBC;
所以CD2=BD2+BC2,故BC⊥BD.
又BC⊥PD,PD∩BD=D,且BD,PD 平面PBD,所以BC⊥平面PBD.
因为BC 平面PBC,所以平面PBC⊥平面PBD.
解 设E为BD的中点,连接PE.
由(1)得BC⊥平面PBD,又BC 平面ABCD,所以平面ABCD⊥平面PBD.
又平面ABCD∩平面PBD=BD,PE 平面PBD,
所以PE⊥平面ABCD.
则A(0,0,0),B(0,2,0),C(2,4,0),D(2,0,0),P(1,1,2).
所以M(2-λ,4-3λ,2λ).
取x=2λ,得平面ABM的一个法向量n=(2λ,0,λ-2).
同课章节目录
