专题三 立体几何:第1讲 空间几何体及其表面积和体积 课件(共65张PPT)
文档属性
| 名称 | 专题三 立体几何:第1讲 空间几何体及其表面积和体积 课件(共65张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 21:18:53 | ||
图片预览











文档简介
(共65张PPT)
上篇 专题三 立体几何
第1讲 空间几何体及其表面积和体积
高考定位
简单几何体的表面积与体积计算,主要以选择题、填空题的形式呈现,在解答题中,有时与空间线、面位置关系的证明相结合,面积与体积的计算作为其中的一问.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
B
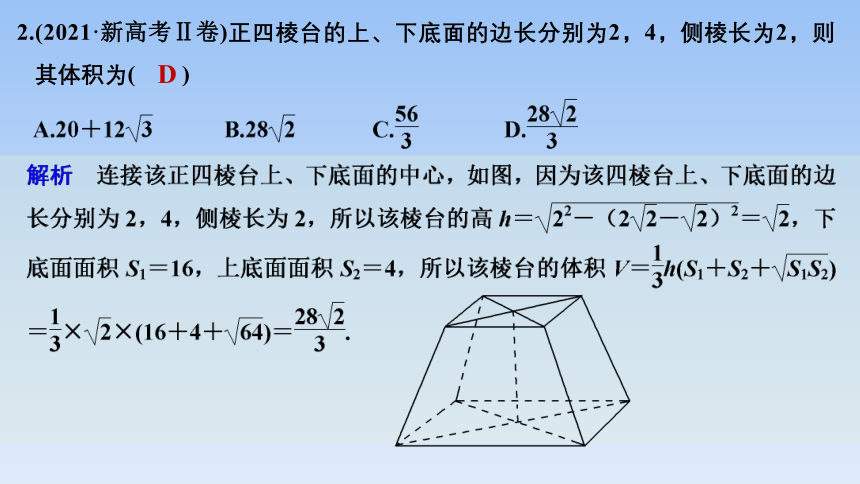
2.(2021·新高考Ⅱ卷)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
D
3.(2021·全国甲卷)已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥OABC的体积为( )
A
A.3π B.4π C.9π D.12π
B
可得R=2,所以AB=AD+BD=4BD=4,
所以BD=1,AD=3.
因为CD⊥AB,则∠CAD+∠ACD=∠BCD+∠ACD=90°,
所以∠CAD=∠BCD,又因为∠ADC=∠BDC,所以△ACD∽△CBD,
5.(2020·全国Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
C
解析 设正四棱锥的底面正方形的边长为a,高为h,侧面三角形底边上的高(斜高)为h′.
6.(2021·全国甲卷)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为________.
39π
1.空间几何体的两组常用公式
(1)柱体、锥体、台体和球的表面积公式:
①圆柱的表面积S=2πr(r+l);
②圆锥的表面积S=πr(r+l);
③圆台的表面积S=π(r′2+r2+r′l+rl);
④球的表面积S=4πR2.
2
热点聚焦 分类突破
热点一 空间几何体的表面积
A.24-3π B.24-π C.24+π D.24+5π
B
(2)(多选)等腰直角三角形的直角边长为1,现将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为( )
AB
1.求空间几何体的表面积,首先要掌握几何体的表面积公式,其次把不规则几何体分割成几个规则的几何体.
2.(1)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.
(2)旋转体的表面积问题注意其侧面展开图的应用.
探究提高
【训练1】 (1)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
B
(2)(2021·惠州二调)某同学在参加《通用技术》实践课时,制作了一个实心工艺品(如图所示).该工艺品可以看成是一个球被一个棱长为8的正方体的6个面所截后剩余的部分(球心与正方体的中心重合).若其中一个截面圆的周长为6π,则该球的半径为________.现给出定义:球面被平面所截得的一部分叫做球冠,截得的截面圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高.如果球面的半径是R,球冠的高是h,那么球冠的表面积计算公式是S=2πRh,由此可知,该实心工艺品的表面积是________.
5
94π
解析 设截面圆的半径为r,则球心到某一截面的距离为正方体棱长的一半,即距离为4,根据截面圆的周长为6π,可得6π=2πr,解得r=3,故R2=32+42=25,得R=5.如图,O为球心,O1为截面圆的圆心,B为球面上一点,A为截面圆上一点,则OA=OB=R=5,且OO1=4,所以球冠的高h=O1B=OB-OO1=1,所以所截得的一个球冠的表面积S=2πRh=2π×5×1=10π,又截面圆的面积为πr2=9π,所以该实心工艺品的表面积为4πR2-6S+6×9π=100π-60π+54π=94π.
热点二 空间几何体的体积
【例2】 (1)(2021·济南联考)正四面体ABCD的体积为4,O为其中心,正四面体EFGH与正四面体ABCD关于点O对称,则这两个正四面体公共部分的体积为( )
C
解析 如图,点I,J,K,L,M,N分别是边AB,AC,AD,BC,CD,DB的中点,这两个正四面体公共部分为多面体IJKLMN.
三棱锥A-IJK是正四面体,其棱长为正四面体ABCD棱长的一半,
(2)如图,在直角梯形ABCD中,AD=AB=4,BC=2,沿中位线EF折起,使得∠AEB为直角,连接AB,CD,则所得的几何体的体积为________.
6
解析 法一 过C作与底面ABE平行的截面CMN,如图(1),截面CMN把这个几何体分割为直三棱柱ABE-MCN和四棱锥C-MNFD.
图(1)
所以所求几何体的体积为V1+V2=6.
法二 如图(2),连接AC,EC,则几何体分割为四棱锥C-ADFE和三棱锥
C-ABE.
图(2)
法三 如图(3),延长BC至点M,使得CM=2,延长EF至点N,使得FN=1,连接DM,MN,DN,得到直三棱柱ABE-DMN,所以所求几何体的体积等于直三棱柱ABE-DMN
图(3)
的体积减去四棱锥D-CMNF的体积.
所以所求几何体的体积为VABE-DMN-VD-CMNF=8-2=6.
1.求三棱锥的体积:等体积转化是常用的方法,转换原则是其高易求,底面放在已知几何体的某一面上.
2.求不规则几何体的体积:常采用分割或补形的方法,将不规则几何体转化为规则几何体以易于求解.
探究提高
【训练2】 (1)(2021·杭州二模)已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的体积为( )
A
解析 设圆锥的底面半径为r,母线长为l,
由πl=2πr,得l=2r,
又S=πr2+πr·2r=3πr2=3π,
所以r2=1,解得r=1,
(2)如图,在Rt△ABC中,AB=BC=1,D和E分别是边BC和AC上异于端点的点,DE⊥BC,将△CDE沿DE折起,使点C到点P的位置,得到四棱锥PABDE,则四棱锥PABDE的体积的最大值为________.
热点三 多面体与球的切、接问题
【例3】 (经典母题)(2021·长沙检测)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是________.
解析 由AB⊥BC,AB=6,BC=8,得AC=10.
要使球的体积V最大,则球与直三棱柱的部分面相切,若球与三个侧面相切,设底面△ABC的内切圆的半径为r.
2r=4>3,不合题意.
球与三棱柱的上、下底面相切时,球的半径R最大.
解析 设底面矩形ABCD的长和宽分别为x,y,
B
【母题迁移2】 若将本例的条件变为“已知三棱锥P-ABC的各顶点都在同一球面上,且PA⊥平面ABC,若该棱锥的体积为1,AB=2,AC=1,∠BAC=60°”,则此球的表面积等于( )
D
解析 AB=2,AC=1,∠BAC=60°,
所以在△ABC中,由余弦定理得:
由题意,三棱锥的外接球的球心是过底面外接圆的圆心垂直于底面与中截面的交点,
所以外接球表面积S=4πR2=16π.
1.与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常是作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.
2.若球面上四点P,A,B,C且PA,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接球问题.
探究提高
【训练3】 (1)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.
解析 当球为圆锥的内切球时,球的半径最大.
如图为圆锥内球半径最大时的轴截面图.
其中球心为O,设其半径为r,AC=3,O1C=1,
A
专题训练 对接高考
3
巩固提升
一、选择题
1.(2021·八省八校一联)斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”,它的画法是:以斐波那契数1,1,2,3,5,…为边长的正方形拼成长方形,然后在每个正方形中画一个圆心角为90°的圆弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.自然界存在很多斐波那契螺旋线的图案,例如向日葵、鹦鹉螺等.如图为该螺旋线的前一部分,如果用接下来的一段圆弧所对应的扇形做圆锥的侧面,那么该圆锥的底面半径为( )
C
2.(2021·福州质检)如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷、佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为45°,则该正四棱锥的一个侧面与底面的面积之比为( )
D
解析 设塔顶是正四棱锥P-ABCD(如图),PO是正四棱锥的高.
设正四棱锥底面边长为a,则底面面积S1=a2,
B
C
设AB的中点为F,连接PF,则PF⊥AB.
因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PF 平面PAB,所以PF⊥平面ABC.
设BC的中点为D,因为∠BAC=90°,所以△ABC外接圆的圆心即BC的中点D.
设△PAB的重心为E,过点E,D分别作平面PAB、平面ABC的垂线,则两垂线的交点O即三棱锥PABC外接球的球心.
5.如图,四边形ABCD是边长为2的正方形,ED⊥平面ABCD,FC⊥平面ABCD,ED=2FC=2,则四面体ABEF的体积为( )
B
解析 ∵ED⊥平面ABCD且AD 平面ABCD,
∴ED⊥AD.
∵在正方形ABCD中,AD⊥DC,又DC∩ED=D,DC,ED 平面CDEF,
∴AD⊥平面CDEF.
6.(多选)若长方体ABCD-A1B1C1D1的长、宽、高分别为3,2,1,则( )
BC
解析 长方体的表面积为2×(3×2+3×1+2×1)=22,A错误.长方体的体积为3×2×1=6,B正确.如图1所示,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,将侧面ABB1A1和侧面BCC1B1展开,如图2所示.
A.AC⊥AF
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
AD
解析 由题意及图形知,当点F与点B1重合时,∠CAF=60°,故A错误;由正方体ABCDA1B1C1D1的两个底面平行,EF 平面A1B1C1D1,知EF∥平面ABCD,故B正确;由几何体的性质及图形知,三角形BEF的面积是定值,点A到平面DD1B1B的距离是定值,故可得三棱锥ABEF的体积为定值,故C正确;由图形可以看出,B到直线EF的距离与A与直线EF的距离不相等,故△AEF的面积与△BEF的面积不相等,故D错误.故选AD.
二、填空题
8.(2021·唐山二模)已知圆锥的侧面展开图是半径为2的半圆,则该圆锥的体积为_______________________.
解析 设圆锥的底面圆半径为r,母线长为l,由题意可知,l=2,侧面展开图的弧长为2π,则2π=2πr,r=1,
9.(2021·八省联考)已知圆台上、下底面的圆周都在一个直径为10的球面上,其上、下底面半径分别为4和5,则该圆台的体积为________.
61π
解析 圆台的下底面半径为5,故下底面在球的大圆上,如图.设球的球心为O,圆台上底面的圆心为O′,则圆台的高
11.(2021·长沙调研)在三棱锥P-ABC中,PA⊥平面ABC,△ABC是正三角形,AB=2,点A到平面PBC的距离为1,则PA=________,三棱锥P-ABC的外接球的表面积是________.
解析 如图,过点A作AD⊥BC于点D,连接PD,过点A作AH⊥PD于点H,则易知AH⊥平面PBC,所以AH为点A到平面PBC的距离,即AH=1.
将三棱锥PABC补形成三棱柱PQRABC,设△PQR,△ABC的中心分别为O1,O2,连接O1O2,取O1O2的中点O,则O为三棱锥PABC的外接球的球心.
能力突破
12.(多选)(2021·唐山二模)将边长为a的正方形ABCD沿对角线BD折起得到三棱锥A′BCD,且A′C=a,则下列结论正确的是( )
ABD
解析 对于A,取BD的中点O,连接A′O,CO,则OA′⊥BD,OC⊥BD,又OA′∩OC=O,OA′,OC 平面A′OC,所以BD⊥平面A′OC,又A′C 平面A′OC,所以A′C⊥BD,所以A正确;
13.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,BC=CD=2AB=2,PA=3,E是PD的中点.
(1)证明:AE∥平面PBC;
证明 取PC的中点F,连接EF,BF,如图所示.
因为E,F分别为PD,PC的中点,
又CD=2AB,AB∥CD,
所以EF∥AB且EF=AB,
所以四边形AEFB是平行四边形,所以AE∥BF,
又因为AE 平面PBC,BF 平面PBC,所以AE∥平面PBC.
所以AC2+AB2=BC2,即AB⊥AC.
因为E是PD的中点,
(1)求四棱锥的总曲率;
解 由题意可知四棱锥的总曲率等于四棱锥各顶点的曲率之和.
可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知:四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形,
所以四棱锥的表面内角和由4个三角形内角和1个四边形内角组成,则其总曲率为2π×5-(4π+2π)=4π.
(2)若多面体满足:顶点数-棱数+面数=2,证明:这类多面体的总曲率是常数.
证明 设顶点数、棱数、面数分别为n,l,m,
所以有n-l+m=2.
设第m个面的棱数为xm,所以x1+x2+…+xm=2l,
所以总曲率为
2πn-π[(x1-2)+(x2-2)+…+(xm-2)]=2πn-π(2l-2m)=2π(n-l+m)=4π,
所以这类多面体的总曲率是常数.
上篇 专题三 立体几何
第1讲 空间几何体及其表面积和体积
高考定位
简单几何体的表面积与体积计算,主要以选择题、填空题的形式呈现,在解答题中,有时与空间线、面位置关系的证明相结合,面积与体积的计算作为其中的一问.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
B
2.(2021·新高考Ⅱ卷)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
D
3.(2021·全国甲卷)已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥OABC的体积为( )
A
A.3π B.4π C.9π D.12π
B
可得R=2,所以AB=AD+BD=4BD=4,
所以BD=1,AD=3.
因为CD⊥AB,则∠CAD+∠ACD=∠BCD+∠ACD=90°,
所以∠CAD=∠BCD,又因为∠ADC=∠BDC,所以△ACD∽△CBD,
5.(2020·全国Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
C
解析 设正四棱锥的底面正方形的边长为a,高为h,侧面三角形底边上的高(斜高)为h′.
6.(2021·全国甲卷)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为________.
39π
1.空间几何体的两组常用公式
(1)柱体、锥体、台体和球的表面积公式:
①圆柱的表面积S=2πr(r+l);
②圆锥的表面积S=πr(r+l);
③圆台的表面积S=π(r′2+r2+r′l+rl);
④球的表面积S=4πR2.
2
热点聚焦 分类突破
热点一 空间几何体的表面积
A.24-3π B.24-π C.24+π D.24+5π
B
(2)(多选)等腰直角三角形的直角边长为1,现将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为( )
AB
1.求空间几何体的表面积,首先要掌握几何体的表面积公式,其次把不规则几何体分割成几个规则的几何体.
2.(1)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.
(2)旋转体的表面积问题注意其侧面展开图的应用.
探究提高
【训练1】 (1)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
B
(2)(2021·惠州二调)某同学在参加《通用技术》实践课时,制作了一个实心工艺品(如图所示).该工艺品可以看成是一个球被一个棱长为8的正方体的6个面所截后剩余的部分(球心与正方体的中心重合).若其中一个截面圆的周长为6π,则该球的半径为________.现给出定义:球面被平面所截得的一部分叫做球冠,截得的截面圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高.如果球面的半径是R,球冠的高是h,那么球冠的表面积计算公式是S=2πRh,由此可知,该实心工艺品的表面积是________.
5
94π
解析 设截面圆的半径为r,则球心到某一截面的距离为正方体棱长的一半,即距离为4,根据截面圆的周长为6π,可得6π=2πr,解得r=3,故R2=32+42=25,得R=5.如图,O为球心,O1为截面圆的圆心,B为球面上一点,A为截面圆上一点,则OA=OB=R=5,且OO1=4,所以球冠的高h=O1B=OB-OO1=1,所以所截得的一个球冠的表面积S=2πRh=2π×5×1=10π,又截面圆的面积为πr2=9π,所以该实心工艺品的表面积为4πR2-6S+6×9π=100π-60π+54π=94π.
热点二 空间几何体的体积
【例2】 (1)(2021·济南联考)正四面体ABCD的体积为4,O为其中心,正四面体EFGH与正四面体ABCD关于点O对称,则这两个正四面体公共部分的体积为( )
C
解析 如图,点I,J,K,L,M,N分别是边AB,AC,AD,BC,CD,DB的中点,这两个正四面体公共部分为多面体IJKLMN.
三棱锥A-IJK是正四面体,其棱长为正四面体ABCD棱长的一半,
(2)如图,在直角梯形ABCD中,AD=AB=4,BC=2,沿中位线EF折起,使得∠AEB为直角,连接AB,CD,则所得的几何体的体积为________.
6
解析 法一 过C作与底面ABE平行的截面CMN,如图(1),截面CMN把这个几何体分割为直三棱柱ABE-MCN和四棱锥C-MNFD.
图(1)
所以所求几何体的体积为V1+V2=6.
法二 如图(2),连接AC,EC,则几何体分割为四棱锥C-ADFE和三棱锥
C-ABE.
图(2)
法三 如图(3),延长BC至点M,使得CM=2,延长EF至点N,使得FN=1,连接DM,MN,DN,得到直三棱柱ABE-DMN,所以所求几何体的体积等于直三棱柱ABE-DMN
图(3)
的体积减去四棱锥D-CMNF的体积.
所以所求几何体的体积为VABE-DMN-VD-CMNF=8-2=6.
1.求三棱锥的体积:等体积转化是常用的方法,转换原则是其高易求,底面放在已知几何体的某一面上.
2.求不规则几何体的体积:常采用分割或补形的方法,将不规则几何体转化为规则几何体以易于求解.
探究提高
【训练2】 (1)(2021·杭州二模)已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的体积为( )
A
解析 设圆锥的底面半径为r,母线长为l,
由πl=2πr,得l=2r,
又S=πr2+πr·2r=3πr2=3π,
所以r2=1,解得r=1,
(2)如图,在Rt△ABC中,AB=BC=1,D和E分别是边BC和AC上异于端点的点,DE⊥BC,将△CDE沿DE折起,使点C到点P的位置,得到四棱锥PABDE,则四棱锥PABDE的体积的最大值为________.
热点三 多面体与球的切、接问题
【例3】 (经典母题)(2021·长沙检测)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是________.
解析 由AB⊥BC,AB=6,BC=8,得AC=10.
要使球的体积V最大,则球与直三棱柱的部分面相切,若球与三个侧面相切,设底面△ABC的内切圆的半径为r.
2r=4>3,不合题意.
球与三棱柱的上、下底面相切时,球的半径R最大.
解析 设底面矩形ABCD的长和宽分别为x,y,
B
【母题迁移2】 若将本例的条件变为“已知三棱锥P-ABC的各顶点都在同一球面上,且PA⊥平面ABC,若该棱锥的体积为1,AB=2,AC=1,∠BAC=60°”,则此球的表面积等于( )
D
解析 AB=2,AC=1,∠BAC=60°,
所以在△ABC中,由余弦定理得:
由题意,三棱锥的外接球的球心是过底面外接圆的圆心垂直于底面与中截面的交点,
所以外接球表面积S=4πR2=16π.
1.与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常是作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.
2.若球面上四点P,A,B,C且PA,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接球问题.
探究提高
【训练3】 (1)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.
解析 当球为圆锥的内切球时,球的半径最大.
如图为圆锥内球半径最大时的轴截面图.
其中球心为O,设其半径为r,AC=3,O1C=1,
A
专题训练 对接高考
3
巩固提升
一、选择题
1.(2021·八省八校一联)斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”,它的画法是:以斐波那契数1,1,2,3,5,…为边长的正方形拼成长方形,然后在每个正方形中画一个圆心角为90°的圆弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.自然界存在很多斐波那契螺旋线的图案,例如向日葵、鹦鹉螺等.如图为该螺旋线的前一部分,如果用接下来的一段圆弧所对应的扇形做圆锥的侧面,那么该圆锥的底面半径为( )
C
2.(2021·福州质检)如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷、佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为45°,则该正四棱锥的一个侧面与底面的面积之比为( )
D
解析 设塔顶是正四棱锥P-ABCD(如图),PO是正四棱锥的高.
设正四棱锥底面边长为a,则底面面积S1=a2,
B
C
设AB的中点为F,连接PF,则PF⊥AB.
因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PF 平面PAB,所以PF⊥平面ABC.
设BC的中点为D,因为∠BAC=90°,所以△ABC外接圆的圆心即BC的中点D.
设△PAB的重心为E,过点E,D分别作平面PAB、平面ABC的垂线,则两垂线的交点O即三棱锥PABC外接球的球心.
5.如图,四边形ABCD是边长为2的正方形,ED⊥平面ABCD,FC⊥平面ABCD,ED=2FC=2,则四面体ABEF的体积为( )
B
解析 ∵ED⊥平面ABCD且AD 平面ABCD,
∴ED⊥AD.
∵在正方形ABCD中,AD⊥DC,又DC∩ED=D,DC,ED 平面CDEF,
∴AD⊥平面CDEF.
6.(多选)若长方体ABCD-A1B1C1D1的长、宽、高分别为3,2,1,则( )
BC
解析 长方体的表面积为2×(3×2+3×1+2×1)=22,A错误.长方体的体积为3×2×1=6,B正确.如图1所示,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,将侧面ABB1A1和侧面BCC1B1展开,如图2所示.
A.AC⊥AF
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
AD
解析 由题意及图形知,当点F与点B1重合时,∠CAF=60°,故A错误;由正方体ABCDA1B1C1D1的两个底面平行,EF 平面A1B1C1D1,知EF∥平面ABCD,故B正确;由几何体的性质及图形知,三角形BEF的面积是定值,点A到平面DD1B1B的距离是定值,故可得三棱锥ABEF的体积为定值,故C正确;由图形可以看出,B到直线EF的距离与A与直线EF的距离不相等,故△AEF的面积与△BEF的面积不相等,故D错误.故选AD.
二、填空题
8.(2021·唐山二模)已知圆锥的侧面展开图是半径为2的半圆,则该圆锥的体积为_______________________.
解析 设圆锥的底面圆半径为r,母线长为l,由题意可知,l=2,侧面展开图的弧长为2π,则2π=2πr,r=1,
9.(2021·八省联考)已知圆台上、下底面的圆周都在一个直径为10的球面上,其上、下底面半径分别为4和5,则该圆台的体积为________.
61π
解析 圆台的下底面半径为5,故下底面在球的大圆上,如图.设球的球心为O,圆台上底面的圆心为O′,则圆台的高
11.(2021·长沙调研)在三棱锥P-ABC中,PA⊥平面ABC,△ABC是正三角形,AB=2,点A到平面PBC的距离为1,则PA=________,三棱锥P-ABC的外接球的表面积是________.
解析 如图,过点A作AD⊥BC于点D,连接PD,过点A作AH⊥PD于点H,则易知AH⊥平面PBC,所以AH为点A到平面PBC的距离,即AH=1.
将三棱锥PABC补形成三棱柱PQRABC,设△PQR,△ABC的中心分别为O1,O2,连接O1O2,取O1O2的中点O,则O为三棱锥PABC的外接球的球心.
能力突破
12.(多选)(2021·唐山二模)将边长为a的正方形ABCD沿对角线BD折起得到三棱锥A′BCD,且A′C=a,则下列结论正确的是( )
ABD
解析 对于A,取BD的中点O,连接A′O,CO,则OA′⊥BD,OC⊥BD,又OA′∩OC=O,OA′,OC 平面A′OC,所以BD⊥平面A′OC,又A′C 平面A′OC,所以A′C⊥BD,所以A正确;
13.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,BC=CD=2AB=2,PA=3,E是PD的中点.
(1)证明:AE∥平面PBC;
证明 取PC的中点F,连接EF,BF,如图所示.
因为E,F分别为PD,PC的中点,
又CD=2AB,AB∥CD,
所以EF∥AB且EF=AB,
所以四边形AEFB是平行四边形,所以AE∥BF,
又因为AE 平面PBC,BF 平面PBC,所以AE∥平面PBC.
所以AC2+AB2=BC2,即AB⊥AC.
因为E是PD的中点,
(1)求四棱锥的总曲率;
解 由题意可知四棱锥的总曲率等于四棱锥各顶点的曲率之和.
可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知:四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形,
所以四棱锥的表面内角和由4个三角形内角和1个四边形内角组成,则其总曲率为2π×5-(4π+2π)=4π.
(2)若多面体满足:顶点数-棱数+面数=2,证明:这类多面体的总曲率是常数.
证明 设顶点数、棱数、面数分别为n,l,m,
所以有n-l+m=2.
设第m个面的棱数为xm,所以x1+x2+…+xm=2l,
所以总曲率为
2πn-π[(x1-2)+(x2-2)+…+(xm-2)]=2πn-π(2l-2m)=2π(n-l+m)=4π,
所以这类多面体的总曲率是常数.
同课章节目录
