专题二 数列 :第1讲 等差数列与等比数列 课件(共63张PPT)
文档属性
| 名称 | 专题二 数列 :第1讲 等差数列与等比数列 课件(共63张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 21:17:28 | ||
图片预览










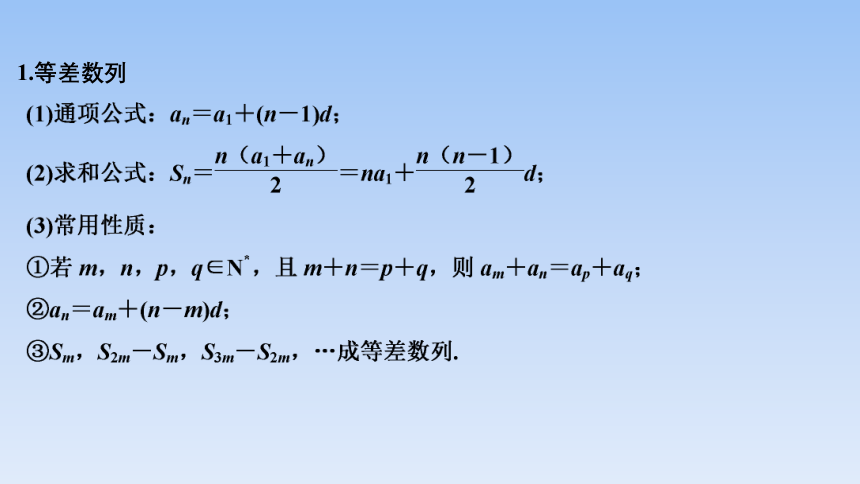
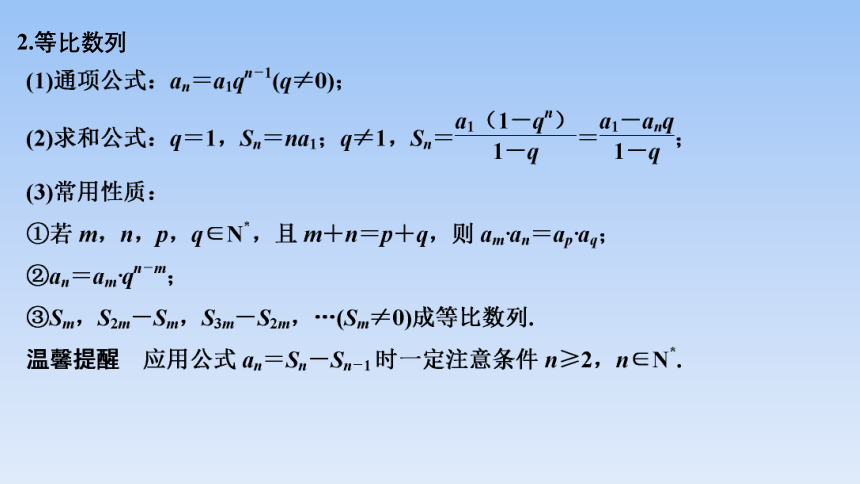
文档简介
(共63张PPT)
上篇 专题二 数列
第1讲 等差数列与等比数列
高考定位
1.等差、等比数列基本运算和性质的考查是高考热点,经常以选择题、填空题的形式出现;2.数列的通项也是高考热点,常在解答题中的第(1)问出现,难度中档以下.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
A.64 B.100 C.128 D.132
C
2.(2021·全国甲卷)记Sn为等比数列{an}的前n项和.若S2=4,S4=6,则S6=( )
A.7 B.8 C.9 D.10
解析 法一 因为S2=4,S4=6,且易知公比q≠±1,所以由等比数列的前n项和公式,得
A
法二 易知S2,S4-S2,S6-S4构成等比数列,由等比中项得S2(S6-S4)=(S4-S2)2,即4(S6-6)=22,所以S6=7.故选A.
3.(2020·全国Ⅱ卷)数列{an}中,a1=2,am+n=aman.若ak+1+ak+2+…+ak+10=215-25,则k=( )
A.2 B.3 C.4 D.5
解析 ∵a1=2,am+n=aman,
令m=1,则an+1=a1an=2an,
∴{an}是以a1=2为首项,2为公比的等比数列,
∴an=2×2n-1=2n.
又∵ak+1+ak+2+…+ak+10=215-25,
C
∴2k+1=25,∴k+1=5,∴k=4.
(1)证明:数列{bn}是等差数列;
证明 因为bn是数列{Sn}的前n项积,
(2)求{an}的通项公式.
1.等差数列
2.等比数列
2
热点聚焦 分类突破
热点一 等差、等比数列的基本运算
【例1】 设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.
(1)求{an}的通项公式;
解 设{an}的公差为d.
因为a1=-10,
所以a2=-10+d,a3=-10+2d,a4=-10+3d.
因为a2+10,a3+8,a4+6成等比数列,
所以(a3+8)2=(a2+10)(a4+6).
所以(-2+2d)2=d(-4+3d).
解得d=2.
所以an=a1+(n-1)d=2n-12.
(2)记{an}的前n项和为Sn,求Sn的最小值.
解 法一 由(1)知,an=2n-12.
则当n≥7时,an>0;
当n=6时,an=0;
当n<6时,an<0;
所以Sn的最小值为S5=S6=-30.
所以当n=5或n=6时,Sn的最小值为S5=S6=-30.
1.等差(比)数列基本运算的解题途径:
(1)设基本量a1和公差d(公比q).
(2)列、解方程组:把条件转化为关于a1和d(q)的方程(组),然后求解,注意整体计算,以减少运算量.
2.第(2)题求出基本量a1与公差d,进而由等差数列前n项和公式将结论表示成关于“n”的函数,求出最小值.
探究提高
(1)求数列{an}的通项公式;
解 设各项均为正数的等差数列的公差为d.
(2)设bn=4n-2+3an,若an∈N,求{bn}的前n项和Tn.
解 由于an∈N,所以an=2n+1.
所以bn=4n-2+3an=4n-2+6n+3.
根据等差数列、等比数列的前n项和公式,
热点二 等差(比)数列的性质
【例2】 (1)在等差数列{an}中,a1=-9,a5=-1.记Tn=a1a2…an(n=1,2,…),则数列{Tn}( )
A.有最大项,有最小项 B.有最大项,无最小项
C.无最大项,有最小项 D.无最大项,无最小项
B
则其通项公式为an=a1+(n-1)d=-9+(n-1)×2=2n-11,
由于a1=-9,a2=-7,a3=-5,a4=-3,a5=-1,a6=1,
故数列{Tn}中的正项只有有限项:T2=63,T4=945.
故数列{Tn}中存在最大项,为T4.故选B.
(2)已知数列{an}的各项都为正数,对任意的m,n∈N*,am·an=am+n恒成立,且a3·a5+a4=72,则log2a1+log2a2+…+log2a7=________.
21
解析 因为对任意的m,n∈N*,am·an=am+n恒成立,
所以数列{an}为等比数列,公比为a1.
又a4>0,解得a4=8,
(3)(多选)已知Sn是等差数列{an}(n∈N*)的前n项和,且S5>S6>S4.下列四个结论正确的是( )
A.数列{Sn}中的最大项为S10 B.数列{an}的公差d<0
C.S10>0 D.S11<0
BCD
解析 因为S5>S6>S4,所以a6<0,a5>0且a5+a6>0,所以数列{Sn}中的最大项为S5,A错误;
数列{an}的公差d<0,B正确;
1.利用等差(比)性质求解的关键是抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解.
2.活用函数性质:数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用函数的性质解题.
探究提高
【训练2】 (1)(2021·江南十校联考)已知等差数列{an}的前n项和为Sn,且S80的正整数n的最大值为( )
A.16 B.17 C.18 D.19
C
解析 由S80,
所以等差数列{an}的公差d<0,且a9>0.
故满足Sn>0的正整数n的最大值为18.
解析 令g(x)=(x+a1)(x+a2)…(x+a7),
则f(x)=xg(x),∴f′(x)=g(x)+xg′(x),
∴f′(0)=g(0)=a1a2…a7=1.
BCD
又a1>1,∴0∵lg an=lg(a1qn-1)=lg a1+(n-1)lg q,又lg q<0,
∴{lg an}是公差为lg q的递减的等差数列,A错误;
∵a1>1,01,
当n≥5时,01.
热点三 等差(比)数列的判断与证明
【例3】 (2021·广东重点中学联考)在数列{an}中,a1=5,an=2an-1+2n-1(n≥2,n∈N*).
(1)求a2,a3的值;
解 因为a1=5,且an=2an-1+2n-1(n≥2),
所以a2=2a1+22-1=13,a3=2a2+23-1=33.
探究提高
【训练3】 (2021·全国甲卷)已知数列{an}的各项为正数,记Sn为{an}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立.
解 ①③ ②.
已知{an}是等差数列,a2=3a1.
设数列{an}的公差为d,则a2=3a1=a1+d,得d=2a1,
①② ③.
设数列{an}的公差为d,
②③ ①.
热点四 等差数列与等比数列的综合问题
【例4】 设{an}是等差数列,其前n项和为Sn(n∈N*);{bn}是等比数列,公比大于0,其前n项和为Tn(n∈N*).已知b1=1,b3=b2+2,b4=a3+a5,b5=a4+2a6.
(1)求Sn和Tn;
解 设等比数列{bn}的公比为q(q>0).
由b1=1,b3=b2+2,可得q2-q-2=0.
因为q>0,可得q=2,故bn=2n-1.
设等差数列{an}的公差为d.
由b4=a3+a5,可得a1+3d=4.
由b5=a4+2a6,可得3a1+13d=16,从而a1=1,d=1,
故an=n.
(2)若Sn+(T1+T2+…+Tn)=an+4bn,求正整数n的值.
解 由(1),有
整理得n2-3n-4=0,解得n=-1(舍)或n=4.
所以n的值为4.
1.等差数列与等比数列交汇的问题,常用“基本量法”求解,但有时灵活地运用性质,可使运算简便.
2.数列的通项或前n项和可以看作关于n的函数,然后利用函数的性质求解数列问题.
探究提高
【训练4】 (2021·衡水中学联考)已知等差数列{an}的前n项和为Sn,且S4=S5=-20.
(1)求数列{an}的通项公式;
解 设等差数列{an}的公差为d,
由S4=S5=-20,得4a1+6d=5a1+10d=-20,
解得a1=-8,d=2,
则an=-8+2(n-1)=2n-10.
(2)已知数列{bn}是以4为首项,4为公比的等比数列,若数列{an}与{bn}的公共项为am,记m由小到大构成数列{cn},求{cn}的前n项和Tn.
解 数列{bn}是以4为首项,4为公比的等比数列,
∴bn=4·4n-1=4n(n∈N*).
专题训练 对接高考
3
巩固提升
A.35 B.36 C.45 D.54
B
解析 由等差数列的性质得a2+a8=2a5,
A.4 B.2 C.3 D.5
B
3.(2021·全国甲卷)等比数列{an}的公比为q,前n项和为Sn.设甲:q>0,乙:{Sn}是递增数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
B
解析 当a1<0,q>1时,an=a1qn-1<0,此时数列{Sn}递减,所以甲不是乙的充分条件.当数列{Sn}递增时,有Sn+1-Sn=an+1=a1qn>0,若a1>0,则qn>0(n∈N*),即q>0;若a1<0,则qn<0(n∈N*),不存在,所以甲是乙的必要条件.综上,甲是乙的必要条件但不是充分条件.
A.2 B.7 C.2,7 D.2,3,7
C
此时数列{an}递增.又a2所以数列{an}的“谷值点”为2,7.
5.(多选)(2021·湖北重点中学调研)设等比数列{an}的公比为q,前n项和为Sn,前n项积为Tn,并满足条件a1>1,a2 021·a2 022>1,(a2 021-1)·(a2 022-1)<0,则下列结论中正确的有( )
A.q>1 B.S2 022>S2 021
C.a2 021·a2 023<1 D.T2 021是数列{Tn}中的最大项
BCD
解析 由{an}为等比数列,a1>1,a2 021·a2 022>1及(a2 021-1)·(a2 022-1)<0,
S2 022=S2 021+a2 022>S2 021,故B正确;
因为a1>1,a2>1,…,a2 021>1,06.已知数列{an}满足an+2+an=2an+1+1,且a1=1,a2=5,则a18=( )
A.69 B.105 C.204 D.205
解析 由an+2+an=2an+1+1,得an+2-an+1=an+1-an+1,
则(an+2-an+1)-(an+1-an)=1,
∵a2-a1=5-1=4,
∴数列{an+1-an}是以4为首项,1为公差的等差数列,
an+1-an=4+1×(n-1)=n+3,
则a1=1,a2-a1=4,a3-a2=5,…,an-an-1=n+2,
D
各项相加,得
an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
二、填空题
7.(2021·上海卷)已知等差数列{an}的首项为3,公差为2,则a10=________.
21
解析 由题意,得a10=3+(10-1)×2=21.
解析 由题意可知,S1=2-2a2=1,且Sn=2-2(Sn+1-Sn),
9.(2021·济南模拟)已知等比数列{an}的前n项的乘积为Tn,若T2=T9=512,则T8=________.
4 096
解析 设等比数列{an}的公比为q,
∴a1q5=1.①
三、解答题
10.(2021·广州质检)已知{an}是等差数列,{bn}是等比数列,且{bn}的前n项和为Sn,2a1=b1=2,a5=5(a4-a3),________.在①b5=4(b4-b3),②bn+1=Sn+2这两个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答.
(1)求数列{an}和{bn}的通项公式;
解 若选条件①,b5=4(b4-b3).
设等差数列{an}的公差为d,
∵2a1=2,a5=5(a4-a3),
∴a1+4d=5(a1+3d-a1-2d),∴a1=d=1.
∴an=1+(n-1)×1=n.
设等比数列{bn}的公比为q.
由b1=2,且b5=4(b4-b3),
得b1q4=4(b1q3-b1q2).
∴q2-4q+4=0,解得q=2.
所以{bn}是首项为2,公比为2的等比数列.
故bn=2×2n-1=2n(n∈N*).
若选条件②,bn+1=Sn+2.
令n=1,得b2=S1+2=b1+2=4.
∴数列{bn}是首项为2,公比为2的等比数列.
从而bn=2×2n-1=2n(n∈N*).
(2)求数列{an-bn}的前n项和Tn.
(注:如果选择多个条件分别解答,那么按第一个解答计分.)
解 由(1)知an-bn=n-2n,
∴Tn=(1+2+3+…+n)-(21+22+23+…+2n),
11.(2021·新高考Ⅱ卷)记Sn是公差不为0的等差数列{an}的前n项和,若a3=S5,a2a4=S4.
(1)求数列{an}的通项公式an;
解 由等差数列的性质可得:S5=5a3,则a3=5a3,
∴a3=0.
设等差数列的公差为d,从而有a2a4=(a3-d)(a3+d)=-d2,
S4=a1+a2+a3+a4=(a3-2d)+(a3-d)+a3+(a3+d)=-2d.
∵a2a4=S4,∴-d2=-2d,由于公差不为零,故d=2,
∴数列{an}的通项公式为an=a3+(n-3)d=2n-6.
(2)求使Sn>an成立的n的最小值.
则不等式Sn>an即n2-5n>2n-6,
整理可得:(n-1)(n-6)>0,
解得n<1或n>6,又n为正整数,故n的最小值为7.
能力突破
12.(多选)(2021·长沙联考)在“全面脱贫”行动中,贫困户小王2021年1月初向银行借了扶贫免息贷款10 000元,用于自己开设的农产品土特产品加工厂的原材料进货,因产品质优价廉,上市后供不应求,据测算每月获得的利润是该月月初投入资金的20%,每月月底需缴纳房租600元和水电费400元,余款作为资金全部用于再进货,如此继续.设第n月月底小王手中有现款为an,则(参考数据:1.211≈7.5,1.212≈9), ( )
A.a1=12 000 B.an+1=1.2an-1 000
C.2021年小王的年利润约为40 000元 D.两年后,小王手中现款约达41万
BCD
解析 每月获得的利润是该月月初投入资金的20%,每月月底需缴纳房租600元和水电费400元,
∴a1=(1+20%)×10 000-(600+400)=11 000(元),故A错误;
由题意an+1=1.2an-1 000,故B正确;
由an+1=1.2an-1 000,得an+1-5 000=1.2(an-5 000),
∴数列{an-5 000}是首项为6 000,公比为1.2的等比数列,
∴a12-5 000=6 000×1.211,即a12=6 000×1.211+5 000≈50 000,
则2021年小王的年利润约为50 000-10 000=40 000(元),故C正确;
13.(2021·江南十校联考)已知等比数列{an}的前n项和为Sn,且an+1+λ=3Sn,a3=12,则实数λ的值为________.
解析 等比数列{an}满足an+1+λ=3Sn,①
则an+λ=3Sn-1(n≥2,n∈N*),②
①-②得an+1-an=3Sn-3Sn-1,则an+1=4an,
所以等比数列{an}的公比为4,
14.已知等差数列{an}的公差为-1,且a2+a7+a12=-6.
(1)求数列{an}的通项公式an与其前n项和Sn;
解 由a2+a7+a12=-6,
得a7=-2,∴a1=4,∴an=5-n,
(2)将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn,若存在m∈N*,使得对任意n∈N*,总有Sn解 由题意知b1=4,b2=2,b3=1,
∴{Tn}为递增数列,得4≤Tn<8.
故(Sn)max=S4=S5=10.
若存在m∈N*,使得对任意n∈N*,总有Sn2.
故实数λ的取值范围为(2,+∞).
上篇 专题二 数列
第1讲 等差数列与等比数列
高考定位
1.等差、等比数列基本运算和性质的考查是高考热点,经常以选择题、填空题的形式出现;2.数列的通项也是高考热点,常在解答题中的第(1)问出现,难度中档以下.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
A.64 B.100 C.128 D.132
C
2.(2021·全国甲卷)记Sn为等比数列{an}的前n项和.若S2=4,S4=6,则S6=( )
A.7 B.8 C.9 D.10
解析 法一 因为S2=4,S4=6,且易知公比q≠±1,所以由等比数列的前n项和公式,得
A
法二 易知S2,S4-S2,S6-S4构成等比数列,由等比中项得S2(S6-S4)=(S4-S2)2,即4(S6-6)=22,所以S6=7.故选A.
3.(2020·全国Ⅱ卷)数列{an}中,a1=2,am+n=aman.若ak+1+ak+2+…+ak+10=215-25,则k=( )
A.2 B.3 C.4 D.5
解析 ∵a1=2,am+n=aman,
令m=1,则an+1=a1an=2an,
∴{an}是以a1=2为首项,2为公比的等比数列,
∴an=2×2n-1=2n.
又∵ak+1+ak+2+…+ak+10=215-25,
C
∴2k+1=25,∴k+1=5,∴k=4.
(1)证明:数列{bn}是等差数列;
证明 因为bn是数列{Sn}的前n项积,
(2)求{an}的通项公式.
1.等差数列
2.等比数列
2
热点聚焦 分类突破
热点一 等差、等比数列的基本运算
【例1】 设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.
(1)求{an}的通项公式;
解 设{an}的公差为d.
因为a1=-10,
所以a2=-10+d,a3=-10+2d,a4=-10+3d.
因为a2+10,a3+8,a4+6成等比数列,
所以(a3+8)2=(a2+10)(a4+6).
所以(-2+2d)2=d(-4+3d).
解得d=2.
所以an=a1+(n-1)d=2n-12.
(2)记{an}的前n项和为Sn,求Sn的最小值.
解 法一 由(1)知,an=2n-12.
则当n≥7时,an>0;
当n=6时,an=0;
当n<6时,an<0;
所以Sn的最小值为S5=S6=-30.
所以当n=5或n=6时,Sn的最小值为S5=S6=-30.
1.等差(比)数列基本运算的解题途径:
(1)设基本量a1和公差d(公比q).
(2)列、解方程组:把条件转化为关于a1和d(q)的方程(组),然后求解,注意整体计算,以减少运算量.
2.第(2)题求出基本量a1与公差d,进而由等差数列前n项和公式将结论表示成关于“n”的函数,求出最小值.
探究提高
(1)求数列{an}的通项公式;
解 设各项均为正数的等差数列的公差为d.
(2)设bn=4n-2+3an,若an∈N,求{bn}的前n项和Tn.
解 由于an∈N,所以an=2n+1.
所以bn=4n-2+3an=4n-2+6n+3.
根据等差数列、等比数列的前n项和公式,
热点二 等差(比)数列的性质
【例2】 (1)在等差数列{an}中,a1=-9,a5=-1.记Tn=a1a2…an(n=1,2,…),则数列{Tn}( )
A.有最大项,有最小项 B.有最大项,无最小项
C.无最大项,有最小项 D.无最大项,无最小项
B
则其通项公式为an=a1+(n-1)d=-9+(n-1)×2=2n-11,
由于a1=-9,a2=-7,a3=-5,a4=-3,a5=-1,a6=1,
故数列{Tn}中的正项只有有限项:T2=63,T4=945.
故数列{Tn}中存在最大项,为T4.故选B.
(2)已知数列{an}的各项都为正数,对任意的m,n∈N*,am·an=am+n恒成立,且a3·a5+a4=72,则log2a1+log2a2+…+log2a7=________.
21
解析 因为对任意的m,n∈N*,am·an=am+n恒成立,
所以数列{an}为等比数列,公比为a1.
又a4>0,解得a4=8,
(3)(多选)已知Sn是等差数列{an}(n∈N*)的前n项和,且S5>S6>S4.下列四个结论正确的是( )
A.数列{Sn}中的最大项为S10 B.数列{an}的公差d<0
C.S10>0 D.S11<0
BCD
解析 因为S5>S6>S4,所以a6<0,a5>0且a5+a6>0,所以数列{Sn}中的最大项为S5,A错误;
数列{an}的公差d<0,B正确;
1.利用等差(比)性质求解的关键是抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解.
2.活用函数性质:数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用函数的性质解题.
探究提高
【训练2】 (1)(2021·江南十校联考)已知等差数列{an}的前n项和为Sn,且S8
A.16 B.17 C.18 D.19
C
解析 由S8
所以等差数列{an}的公差d<0,且a9>0.
故满足Sn>0的正整数n的最大值为18.
解析 令g(x)=(x+a1)(x+a2)…(x+a7),
则f(x)=xg(x),∴f′(x)=g(x)+xg′(x),
∴f′(0)=g(0)=a1a2…a7=1.
BCD
又a1>1,∴0
∴{lg an}是公差为lg q的递减的等差数列,A错误;
∵a1>1,0
当n≥5时,0
热点三 等差(比)数列的判断与证明
【例3】 (2021·广东重点中学联考)在数列{an}中,a1=5,an=2an-1+2n-1(n≥2,n∈N*).
(1)求a2,a3的值;
解 因为a1=5,且an=2an-1+2n-1(n≥2),
所以a2=2a1+22-1=13,a3=2a2+23-1=33.
探究提高
【训练3】 (2021·全国甲卷)已知数列{an}的各项为正数,记Sn为{an}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立.
解 ①③ ②.
已知{an}是等差数列,a2=3a1.
设数列{an}的公差为d,则a2=3a1=a1+d,得d=2a1,
①② ③.
设数列{an}的公差为d,
②③ ①.
热点四 等差数列与等比数列的综合问题
【例4】 设{an}是等差数列,其前n项和为Sn(n∈N*);{bn}是等比数列,公比大于0,其前n项和为Tn(n∈N*).已知b1=1,b3=b2+2,b4=a3+a5,b5=a4+2a6.
(1)求Sn和Tn;
解 设等比数列{bn}的公比为q(q>0).
由b1=1,b3=b2+2,可得q2-q-2=0.
因为q>0,可得q=2,故bn=2n-1.
设等差数列{an}的公差为d.
由b4=a3+a5,可得a1+3d=4.
由b5=a4+2a6,可得3a1+13d=16,从而a1=1,d=1,
故an=n.
(2)若Sn+(T1+T2+…+Tn)=an+4bn,求正整数n的值.
解 由(1),有
整理得n2-3n-4=0,解得n=-1(舍)或n=4.
所以n的值为4.
1.等差数列与等比数列交汇的问题,常用“基本量法”求解,但有时灵活地运用性质,可使运算简便.
2.数列的通项或前n项和可以看作关于n的函数,然后利用函数的性质求解数列问题.
探究提高
【训练4】 (2021·衡水中学联考)已知等差数列{an}的前n项和为Sn,且S4=S5=-20.
(1)求数列{an}的通项公式;
解 设等差数列{an}的公差为d,
由S4=S5=-20,得4a1+6d=5a1+10d=-20,
解得a1=-8,d=2,
则an=-8+2(n-1)=2n-10.
(2)已知数列{bn}是以4为首项,4为公比的等比数列,若数列{an}与{bn}的公共项为am,记m由小到大构成数列{cn},求{cn}的前n项和Tn.
解 数列{bn}是以4为首项,4为公比的等比数列,
∴bn=4·4n-1=4n(n∈N*).
专题训练 对接高考
3
巩固提升
A.35 B.36 C.45 D.54
B
解析 由等差数列的性质得a2+a8=2a5,
A.4 B.2 C.3 D.5
B
3.(2021·全国甲卷)等比数列{an}的公比为q,前n项和为Sn.设甲:q>0,乙:{Sn}是递增数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
B
解析 当a1<0,q>1时,an=a1qn-1<0,此时数列{Sn}递减,所以甲不是乙的充分条件.当数列{Sn}递增时,有Sn+1-Sn=an+1=a1qn>0,若a1>0,则qn>0(n∈N*),即q>0;若a1<0,则qn<0(n∈N*),不存在,所以甲是乙的必要条件.综上,甲是乙的必要条件但不是充分条件.
A.2 B.7 C.2,7 D.2,3,7
C
此时数列{an}递增.又a2
5.(多选)(2021·湖北重点中学调研)设等比数列{an}的公比为q,前n项和为Sn,前n项积为Tn,并满足条件a1>1,a2 021·a2 022>1,(a2 021-1)·(a2 022-1)<0,则下列结论中正确的有( )
A.q>1 B.S2 022>S2 021
C.a2 021·a2 023<1 D.T2 021是数列{Tn}中的最大项
BCD
解析 由{an}为等比数列,a1>1,a2 021·a2 022>1及(a2 021-1)·(a2 022-1)<0,
S2 022=S2 021+a2 022>S2 021,故B正确;
因为a1>1,a2>1,…,a2 021>1,0
A.69 B.105 C.204 D.205
解析 由an+2+an=2an+1+1,得an+2-an+1=an+1-an+1,
则(an+2-an+1)-(an+1-an)=1,
∵a2-a1=5-1=4,
∴数列{an+1-an}是以4为首项,1为公差的等差数列,
an+1-an=4+1×(n-1)=n+3,
则a1=1,a2-a1=4,a3-a2=5,…,an-an-1=n+2,
D
各项相加,得
an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
二、填空题
7.(2021·上海卷)已知等差数列{an}的首项为3,公差为2,则a10=________.
21
解析 由题意,得a10=3+(10-1)×2=21.
解析 由题意可知,S1=2-2a2=1,且Sn=2-2(Sn+1-Sn),
9.(2021·济南模拟)已知等比数列{an}的前n项的乘积为Tn,若T2=T9=512,则T8=________.
4 096
解析 设等比数列{an}的公比为q,
∴a1q5=1.①
三、解答题
10.(2021·广州质检)已知{an}是等差数列,{bn}是等比数列,且{bn}的前n项和为Sn,2a1=b1=2,a5=5(a4-a3),________.在①b5=4(b4-b3),②bn+1=Sn+2这两个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答.
(1)求数列{an}和{bn}的通项公式;
解 若选条件①,b5=4(b4-b3).
设等差数列{an}的公差为d,
∵2a1=2,a5=5(a4-a3),
∴a1+4d=5(a1+3d-a1-2d),∴a1=d=1.
∴an=1+(n-1)×1=n.
设等比数列{bn}的公比为q.
由b1=2,且b5=4(b4-b3),
得b1q4=4(b1q3-b1q2).
∴q2-4q+4=0,解得q=2.
所以{bn}是首项为2,公比为2的等比数列.
故bn=2×2n-1=2n(n∈N*).
若选条件②,bn+1=Sn+2.
令n=1,得b2=S1+2=b1+2=4.
∴数列{bn}是首项为2,公比为2的等比数列.
从而bn=2×2n-1=2n(n∈N*).
(2)求数列{an-bn}的前n项和Tn.
(注:如果选择多个条件分别解答,那么按第一个解答计分.)
解 由(1)知an-bn=n-2n,
∴Tn=(1+2+3+…+n)-(21+22+23+…+2n),
11.(2021·新高考Ⅱ卷)记Sn是公差不为0的等差数列{an}的前n项和,若a3=S5,a2a4=S4.
(1)求数列{an}的通项公式an;
解 由等差数列的性质可得:S5=5a3,则a3=5a3,
∴a3=0.
设等差数列的公差为d,从而有a2a4=(a3-d)(a3+d)=-d2,
S4=a1+a2+a3+a4=(a3-2d)+(a3-d)+a3+(a3+d)=-2d.
∵a2a4=S4,∴-d2=-2d,由于公差不为零,故d=2,
∴数列{an}的通项公式为an=a3+(n-3)d=2n-6.
(2)求使Sn>an成立的n的最小值.
则不等式Sn>an即n2-5n>2n-6,
整理可得:(n-1)(n-6)>0,
解得n<1或n>6,又n为正整数,故n的最小值为7.
能力突破
12.(多选)(2021·长沙联考)在“全面脱贫”行动中,贫困户小王2021年1月初向银行借了扶贫免息贷款10 000元,用于自己开设的农产品土特产品加工厂的原材料进货,因产品质优价廉,上市后供不应求,据测算每月获得的利润是该月月初投入资金的20%,每月月底需缴纳房租600元和水电费400元,余款作为资金全部用于再进货,如此继续.设第n月月底小王手中有现款为an,则(参考数据:1.211≈7.5,1.212≈9), ( )
A.a1=12 000 B.an+1=1.2an-1 000
C.2021年小王的年利润约为40 000元 D.两年后,小王手中现款约达41万
BCD
解析 每月获得的利润是该月月初投入资金的20%,每月月底需缴纳房租600元和水电费400元,
∴a1=(1+20%)×10 000-(600+400)=11 000(元),故A错误;
由题意an+1=1.2an-1 000,故B正确;
由an+1=1.2an-1 000,得an+1-5 000=1.2(an-5 000),
∴数列{an-5 000}是首项为6 000,公比为1.2的等比数列,
∴a12-5 000=6 000×1.211,即a12=6 000×1.211+5 000≈50 000,
则2021年小王的年利润约为50 000-10 000=40 000(元),故C正确;
13.(2021·江南十校联考)已知等比数列{an}的前n项和为Sn,且an+1+λ=3Sn,a3=12,则实数λ的值为________.
解析 等比数列{an}满足an+1+λ=3Sn,①
则an+λ=3Sn-1(n≥2,n∈N*),②
①-②得an+1-an=3Sn-3Sn-1,则an+1=4an,
所以等比数列{an}的公比为4,
14.已知等差数列{an}的公差为-1,且a2+a7+a12=-6.
(1)求数列{an}的通项公式an与其前n项和Sn;
解 由a2+a7+a12=-6,
得a7=-2,∴a1=4,∴an=5-n,
(2)将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn,若存在m∈N*,使得对任意n∈N*,总有Sn
∴{Tn}为递增数列,得4≤Tn<8.
故(Sn)max=S4=S5=10.
若存在m∈N*,使得对任意n∈N*,总有Sn
故实数λ的取值范围为(2,+∞).
同课章节目录
