专题二 数列:第2讲 数列求和及综合应用 课件(共77张PPT)
文档属性
| 名称 | 专题二 数列:第2讲 数列求和及综合应用 课件(共77张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 21:16:13 | ||
图片预览






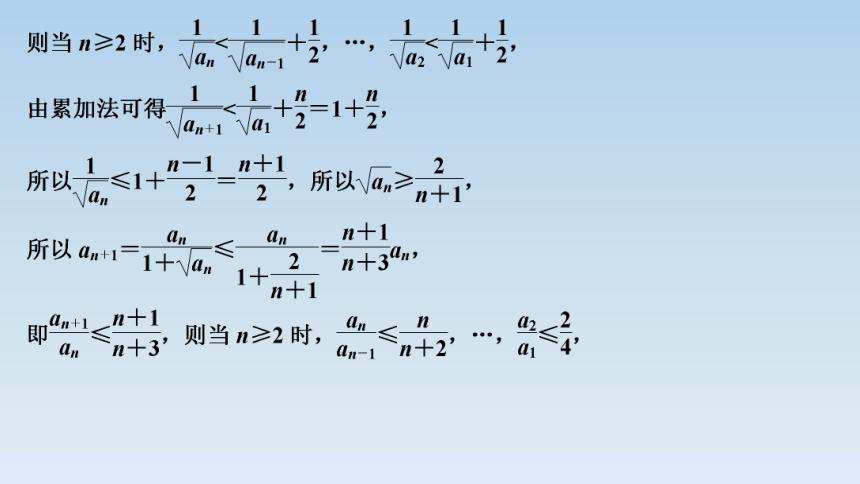
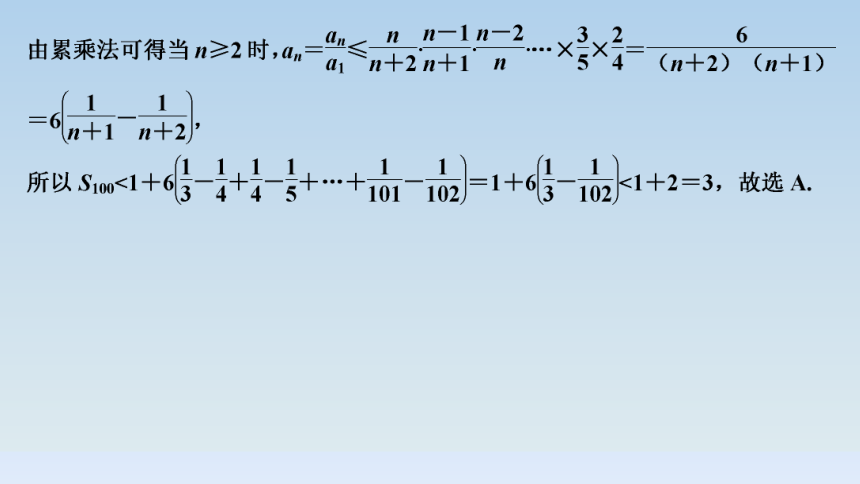



文档简介
(共77张PPT)
上篇 专题二 数列
第2讲 数列求和及综合应用
高考定位
1.高考对数列求和的考查主要以解答题的形式出现,通过分组转化、错位相减、裂项相消等方法求数列的和,难度中档偏下;2.在考查数列运算的同时,将数列与不等式、函数交汇渗透.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
1.(2021·北京卷)数列{an}是递增的整数数列,且a1≥3,a1+a2+a3+…+an=100,则n的最大值为( )
A.9 B.10 C.11 D.12
C
解析 要想n最大,前面的项应该越小越好,3,4,5,6,7,8,9,10,11,12,13,14这12项的和为102,超过了100,故n的最大值为11.如3,4,5,6,7,8,9,10,11,12,25.故选C.
A
3.(多选)(2021·新高考Ⅱ卷)设正整数n=a0·20+a1·2+…+ak-1·2k-1+ak·2k,其中ai∈{0,1}(i=0,1,2,3,…,k),记ω(n)=a0+a1+…+ak,则( )
A.ω(2n)=ω(n) B.ω(2n+3)=ω(n)+1
C.ω(8n+5)=ω(4n+3) D.ω(2n-1)=n
ACD
解 对于A选项,ω(n)=a0+a1+…+ak,2n=0·20+a0·21+a1·22+…+ak-1·2k+ak·2k+1,所以ω(2n)=0+a0+a1+…+ak=ω(n),A选项正确;
对于B选项,取n=2,则2n+3=7=1·20+1·21+1·22,∴ω(7)=3,而2=0·20+1·21,则ω(2)=1,即ω(7)≠ω(2)+1,B选项错误;
对于C选项,8n+5=a0·23+a1·24+…+ak·2k+3+5=1·20+0·21+1·22+a0·23+a1·24+…+ak·2k+3,所以ω(8n+5)=2+a0+a1+…+ak,4n+3=a0·22+a1·23+…+ak·2k+2+3=1·20+1·21+a0·22+a1·23+…+ak·2k+2,所以ω(4n+3)=2+a0+a1+…+ak,因此ω(8n+5)=ω(4n+3),C选项正确;
对于D选项,2n-1=20+21+…+2n-1,故ω(2n-1)=n,D选项正确.故选ACD.
(1)求{an}和{bn}的通项公式;
解 设{an}的公比为q,则an=qn-1.
因为a1,3a2,9a3成等差数列,
2.数列求和
(1)分组转化法:一个数列既不是等差数列,也不是等比数列,若将这个数列适当拆开,重新组合,就会变成几个可以求和的部分,分别求和,然后再合并.
(2)错位相减法:主要用于求数列{an·bn}的前n项和,其中{an},{bn}分别是等差数列和等比数列.
温馨提醒 裂项求和时,易把系数写成它的倒数或忘记系数导致错误.
3.数列与函数、不等式的交汇
数列与函数的综合问题一般是利用函数作为背景,给出数列所满足的条件,通常利用点在曲线上给出Sn的表达式,还有以曲线上的切点为背景的问题,解决这类问题的关键在于利用数列与函数的对应关系,将条件进行准确的转化.数列与不等式的综合问题一般以数列为载体,考查不等关系或恒成立问题.
2
热点聚焦 分类突破
热点一 数列求和
考向1 分组转化法求和
【例1】 已知在等比数列{an}中,a1=2,且a1,a2,a3-2成等差数列.
(1)求数列{an}的通项公式;
解 设等比数列{an}的公比为q,
由a1,a2,a3-2成等差数列,得2a2=a1+a3-2,
则4q=2+2q2-2,解得q=2(q=0舍去).
则an=a1qn-1=2n,n∈N*.
则数列{bn}的前n项和
探究提高
考向2 裂项相消法求和
(1)求数列{an}与{bn}的通项公式;
解 当n=1时,a1=S1=3.
当n≥2时,an=Sn-Sn-1=n+2.
又a1适合上式,∴an=n+2.
∵b2=a2=4,b3=a6=8,
∴bn=b2·qn-2=4×2n-2=2n(n∈N*).
解 cn=log2bn=n,
1.裂项相消求和就是将数列中的每一项裂成两项或多项,使这些裂开的项出现有规律的相互抵消,要注意消去了哪些项,保留了哪些项.
2.消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.
探究提高
(1)求{an}的通项公式;
得(an+1+an)(an+1-an)=2(an+1+an).
又an>0,知an+1+an≠0,
所以an+1-an=2.
因此数列{an}是首项为1,公差为2的等差数列,
所以an=a1+2(n-1)=2n-1.
解 由(1)知
考向3 错位相减法求和
【例3】 (2021·八省八校一联)已知{an}为等差数列,{bn}为等比数列,{bn}的前n项和为Sn,且a1=b1=1,a2=a3-b3,a3=S3+b2.
(1)求数列{an},{bn}的通项公式;
解 设等差数列{an}的公差为d,等比数列{bn}的公比为q.
∵a1=b1=1,a2=a3-b3,a3=S3+b2,
∴an=4n-3,bn=2n-1.
解 ∵{an}是等差数列,∴an+an+2=2an+1.
又由(1)知bn+2=2bn+1,
①-②,得
1.一般地,如果数列{an}是等差数列,{bn}是等比数列,求数列{an·bn}的前n项和时,可采用错位相减法求和,一般是和式两边同乘以等比数列{bn}的公比,然后作差求解.
2.在写“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”,以便下一步准确地写出“Sn-qSn”的表达式.
探究提高
(1)求数列{an}的通项公式;
解 设等差数列{an}的公差为d,
∴an=2n-1,n∈N*.
(2)若bn=2n-1+1,令cn=an·bn,求数列{cn}的前n项和Tn.
解 由(1)及bn=2n-1+1,得cn=(2n-1)·2n-1+(2n-1),
∴Tn=1×20+3×21+5×22+…+(2n-1)·2n-1+[1+3+…+(2n-1)],
设M=1+3+5+…+(2n-1)=n2,
A=1×20+3×21+5×22+…+(2n-1)·2n-1,
则2A=1×2+3×22+5×23+…+(2n-3)·2n-1+(2n-1)·2n,
两式相减得
∴A=2n(2n-3)+3.
∴Tn=A+M=2n(2n-3)+3+n2.
热点二 an与Sn的关系问题
(1)求数列{an}的通项公式;
解 因为an=5Sn+1,n∈N*,
所以an+1=5Sn+1+1,
(2)求数列{cn}的前n项和An,并求出An的最值.
解 由(1)知bn=-1-log2|an|=2n-1,
数列{bn}的前n项和Tn=n2,
因此{An}是单调递增数列,
1.给出Sn与an的递推关系求an,常用思路是:一是利用Sn-Sn-1=an(n≥2)转化为an的递推关系,再求其通项公式;二是转化为Sn的递推关系,先求出Sn与n之间的关系,再求an.
2.由Sn求an时,一定注意分n=1和n≥2两种情况,最后验证两者是否能合为一个式子,若不能,则用分段形式来表示.
探究提高
(1)求数列{an}的通项公式;
∴数列{an}是等差数列,首项为1,公差为1.
∴an=1+n-1=n.
(2)设bn=(1-an)2-a(1-an),若{bn}是递增数列,求实数a的取值范围.
解 bn=(1-an)2-a(1-an)=(n-1)2+a(n-1),
∵{bn}是递增数列,
∴bn+1-bn=n2+an-(n-1)2-a(n-1)
=2n+a-1>0,
即a>1-2n恒成立,∴a>-1,
∴实数a的取值范围是(-1,+∞).
热点三 与数列相关的综合问题
【例5】 (2021·石家庄质检)已知函数f(x)=logk x(k为常数,k>0且k≠1),且数列{f(an)}是首项为4,公差为2的等差数列.
(1)求证:数列{an}是等比数列;
证明 由题意得f(an)=4+2(n-1)=2n+2,
即logk an=2n+2,所以an=k2n+2,
因为常数k>0且k≠1,所以k2为非零常数,
所以数列{an}是以k4为首项,k2为公比的等比数列.
(3)若cn=anlg an,是否存在k∈(0,1),使得数列{cn}是递增数列,若存在,试求实数k的取值范围;若不存在,说明理由.
解 存在.理由如下:
结合(1)知,cn=anlg an=(2n+2)·k2n+2·lg k,
由{cn}单调递增,即 n∈N*,cn所以(n+1)lg k<(n+2)·k2·lg k对n∈N*恒成立.
1.求解数列与函数交汇问题要注意两点:
(1)数列是一类特殊的函数,其定义域是正整数集(或它的有限子集),在求数列最值或不等关系时要特别注意.
(2)解题时准确构造函数,利用函数性质时注意限制条件.
2.本题第(2)问求最值,其实质是利用函数的单调性.第(3)问把{cn}的单调性转化为不等式cn探究提高
(1)求数列{an}的通项公式;
解 因为4Sn+1=3Sn-9,
所以当n≥2时,4Sn=3Sn-1-9,
(2)设数列{bn}满足3bn+(n-4)an=0(n∈N*),记{bn}的前n项和为Tn.若Tn≤λbn对任意n∈N*恒成立,求实数λ的取值范围.
解 因为3bn+(n-4)an=0,
当n=4时,-12≤0恒成立;
专题训练 对接高考
3
巩固提升
一、选择题
1.(2021·人大附中调研)在数列{an}中,已知an=n2+λn,n∈N*,则“a1A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
C
解析 若在数列{an}中,已知an=n2+λn,n∈N*,a1-3.
若数列{an}是单调递增数列,则对任意的n∈N*都满足an+1-an=(n+1)2+λ(n+1)-n2-λn=2n+1+λ>0,
∴λ>-1-2n,即λ>(-1-2n)max=-3,
因此,“a12.数列{an}满足2an+1=an+an+2,且a4,a4 040是函数f(x)=x2-8x+3的两个零点,则a2 022的值为( )
A.4 B.-4 C.4 040 D.-4 040
解析 因为a4,a4 040是函数f(x)=x2-8x+3的两个零点,即a4,a4 040是方程x2-8x+3=0的两个根,所以a4+a4 040=8.
又2an+1=an+an+2,所以数列{an}是等差数列,
所以a4+a4 040=2a2 022=8,所以a2 022=4.
A
3.在等差数列{an}中,a3+a5=a4+7,a10=19,则数列{ancos nπ}(n∈N*)的前2 022项的和为( )
A.1 011 B.1 010 C.2 022 D.2 020
解析 由题意得a3+a5=2a4=a4+7,解得a4=7,
C
则a1=a4-3d=7-3×2=1,所以an=2n-1,
设bn=ancos nπ,
则b1+b2=a1cos π+a2cos 2π=-a1+a2=2,
b3+b4=a3cos 3π+a4cos 4π=-a3+a4=2,……,
∴数列{ancos nπ}(n∈N*)的前2 022项的和
S2 022=(b1+b2)+(b3+b4)+…+(b2 021+b2 022)=2×1 011=2 022.
A.-16 B.-8 C.8 D.16
解析 当n为奇数时,n+1为偶数,
则an=n2-(n+1)2=-2n-1,
所以a1+a3+a5+a7=-(3+7+11+15)=-36.
当n为偶数时,n+1为奇数,
则an=-n2+(n+1)2=2n+1,
则a2+a4+a6+a8=5+9+13+17=44,
所以a1+a2+a3+…+a8=-36+44=8.
C
解析 由题意,知b1=S2=a1+a2,bn+1=S2n+2-S2n,
可得bn=S2n-S2n-2=a2n+a2n-1(n>1,n∈N*).
由{an}为等差数列,知{bn}为等差数列.
由等差数列的性质,显然A,B成立;
选项C中,a2=a1+d,a4=a1+3d,a8=a1+7d.
D
化简得a1d=d2,
A.a3=13 B.数列{3+an}是等比数列
C.an=4n-3 D.Sn=2n+1-3n
AB
即1+2+2an=an+1,即an+1=3+2an,an+1+3=2(an+3),
所以数列{an+3}是以a1+3=4为首项,2为公比的等比数列,
于是an+3=4×2n-1=2n+1,所以an=2n+1-3,所以a3=24-3=13,所以A,B选项正确,C选项不正确.
又S2=a1+a2=1+5=6,而22+1-3×2=2,所以D选项不正确,故选AB.
99
8.(2021·宿迁质检)已知{an}是公差d不为零的等差数列,a5=14,且a1,a3,a11成等比数列,设bn=(-1)n+1an,数列{bn}的前n项的和为Sn,则S2 021=________.
3 032
解析 由于a1,a3,a11成等比数列,
∴14d2=3a5d.
又d≠0,a5=14,知d=3,
因此an=a5+(n-5)×3=3n-1,bn=(-1)n+1(3n-1).
9.(2021·湖南六校联考)把数列{2n+1}(n∈N*)中的各项依次按第1个括号一个数,第2个括号两个数,第3个括号三个数,第4个括号四个数,第5个括号一个数,…,进行排列,得到如下排列;(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43),…,则第100个括号内各数之和为________.
1 992
解析 把每4个括号算作一组,由题意可知每组共有10个数,则第100个括号为第25组中的最后一个括号,前24组共有240个数,第25组的前3个括号内共有6个数,所以第100个括号内的数是数列{2n+1}的第247,248,249,250项,则第100个括号内的各数之和为(2×247+1+2×250+1)×2=1 992.
三、解答题
问题:是否存在数列{an}(n∈N*),其前n项和为Sn,且a1=1,a3=4,________?
(注:如果选择多个条件分别解答,那么按第一个解答计分.)
所以该数列不存在.
如果选择②an+1=an+d(n∈N*,d为常数),则数列{an}为等差数列,
如果选择③an+1=qan(q>0,n∈N*,q为常数),则数列{an}为等比数列,
(1)求{an}的通项公式;
所以当n=1时,a1=S1=1,
又n=1时符合上式,所以an=n.
b2k+1-b2k-1=(2k+1)-(2k-1)=2,
则{b2k-1}是以1为首项,2为公差的等差数列;
能力突破
12.(多选)(2021·江苏调考)斐波那契螺旋线也称黄金螺旋线,是根据斐波那契数列画出来的螺旋曲线.在一个黄金矩形(宽长比约等于0.618)里先以宽为边长作正方形,然后在剩下小的矩形里以其宽为边长作正方形,如此循环下去,再在每个正方形里画出一段四分之一圆弧,最后顺次连接,就可得到一条“黄金螺旋线”.达·芬奇的《蒙娜丽莎》(如图),希腊雅典卫城的帕特农神庙等都符合这个曲线.现将每一段黄金螺线与其所在的正方形所围成的扇形半径设为an(n∈N*),数列{an}满足a1=a2=1,an=an-1+an-2(n≥3),再将扇形面积设为bn(n∈N*),则( )
ABD
A.4(b2 020-b2 019)=πa2 018a2 021
B.a1+a2+a3+…+a2 019=a2 021-1
C.a+a+a+…+a=2a2 019a2 021
D.a2 019a2 021-a+a2 018a2 020-a=0
因为an=an-1+an-2(n≥3),所以a3=a5-a4,a4=a6-a5,a5=a7-a6,…,a2 018=a2 020-a2 019,a2 019=a2 021-a2 020,又a4=a3+a2=a1+a2+a2=3,所以a1+a2+a3+…+a2 019=a2 021-1,故B正确;
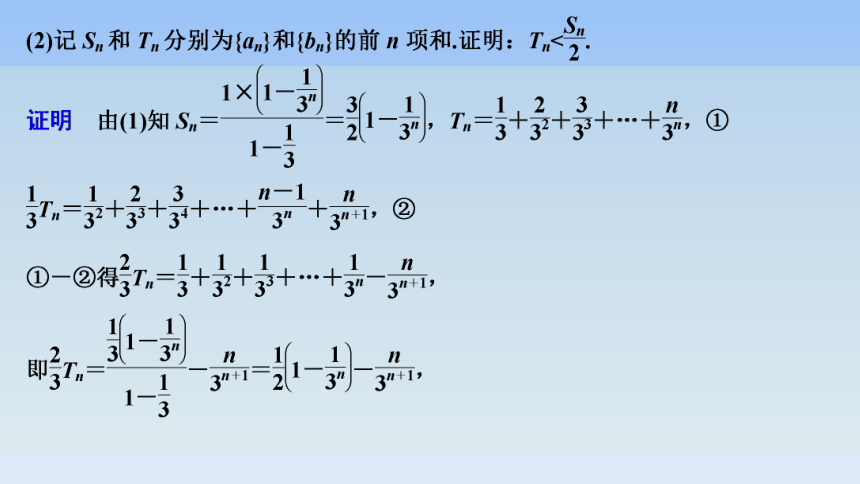
13.(2021·湖北十校一联)已知等差数列{an}与正项等比数列{bn}满足a1=b1=3,且b3-a3,20,a5+b2既是等差数列,又是等比数列.
(1)求数列{an}和{bn}的通项公式;
解 设等差数列{an}的公差为d,等比数列{bn}的公比为q(q>0),
由题意得20=b3-a3=a5+b2,
所以an=2n+1,bn=3n.
选②,cn=anbn=(2n+1)3n,
则Sn=c1+c2+…+cn=3×3+5×32+…+(2n+1)3n,
3Sn=3×32+5×33+…+(2n+1)3n+1,
14.(2021·天津卷)已知{an}是公差为2的等差数列,其前8项和为64.{bn}是公比大于0的等比数列,b1=4,b3-b2=48.
(1)求{an}和{bn}的通项公式;
解 因为{an}是公差为2的等差数列,其前8项和为64,
所以an=a1+2(n-1)=2n-1,n∈N*.
设等比数列{bn}的公比为q(q>0),
所以b3-b2=b1q2-b1q=4(q2-q)=48,解得q=4(负值舍去),
所以bn=b1qn-1=4n ,n∈N*.
上篇 专题二 数列
第2讲 数列求和及综合应用
高考定位
1.高考对数列求和的考查主要以解答题的形式出现,通过分组转化、错位相减、裂项相消等方法求数列的和,难度中档偏下;2.在考查数列运算的同时,将数列与不等式、函数交汇渗透.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
1.(2021·北京卷)数列{an}是递增的整数数列,且a1≥3,a1+a2+a3+…+an=100,则n的最大值为( )
A.9 B.10 C.11 D.12
C
解析 要想n最大,前面的项应该越小越好,3,4,5,6,7,8,9,10,11,12,13,14这12项的和为102,超过了100,故n的最大值为11.如3,4,5,6,7,8,9,10,11,12,25.故选C.
A
3.(多选)(2021·新高考Ⅱ卷)设正整数n=a0·20+a1·2+…+ak-1·2k-1+ak·2k,其中ai∈{0,1}(i=0,1,2,3,…,k),记ω(n)=a0+a1+…+ak,则( )
A.ω(2n)=ω(n) B.ω(2n+3)=ω(n)+1
C.ω(8n+5)=ω(4n+3) D.ω(2n-1)=n
ACD
解 对于A选项,ω(n)=a0+a1+…+ak,2n=0·20+a0·21+a1·22+…+ak-1·2k+ak·2k+1,所以ω(2n)=0+a0+a1+…+ak=ω(n),A选项正确;
对于B选项,取n=2,则2n+3=7=1·20+1·21+1·22,∴ω(7)=3,而2=0·20+1·21,则ω(2)=1,即ω(7)≠ω(2)+1,B选项错误;
对于C选项,8n+5=a0·23+a1·24+…+ak·2k+3+5=1·20+0·21+1·22+a0·23+a1·24+…+ak·2k+3,所以ω(8n+5)=2+a0+a1+…+ak,4n+3=a0·22+a1·23+…+ak·2k+2+3=1·20+1·21+a0·22+a1·23+…+ak·2k+2,所以ω(4n+3)=2+a0+a1+…+ak,因此ω(8n+5)=ω(4n+3),C选项正确;
对于D选项,2n-1=20+21+…+2n-1,故ω(2n-1)=n,D选项正确.故选ACD.
(1)求{an}和{bn}的通项公式;
解 设{an}的公比为q,则an=qn-1.
因为a1,3a2,9a3成等差数列,
2.数列求和
(1)分组转化法:一个数列既不是等差数列,也不是等比数列,若将这个数列适当拆开,重新组合,就会变成几个可以求和的部分,分别求和,然后再合并.
(2)错位相减法:主要用于求数列{an·bn}的前n项和,其中{an},{bn}分别是等差数列和等比数列.
温馨提醒 裂项求和时,易把系数写成它的倒数或忘记系数导致错误.
3.数列与函数、不等式的交汇
数列与函数的综合问题一般是利用函数作为背景,给出数列所满足的条件,通常利用点在曲线上给出Sn的表达式,还有以曲线上的切点为背景的问题,解决这类问题的关键在于利用数列与函数的对应关系,将条件进行准确的转化.数列与不等式的综合问题一般以数列为载体,考查不等关系或恒成立问题.
2
热点聚焦 分类突破
热点一 数列求和
考向1 分组转化法求和
【例1】 已知在等比数列{an}中,a1=2,且a1,a2,a3-2成等差数列.
(1)求数列{an}的通项公式;
解 设等比数列{an}的公比为q,
由a1,a2,a3-2成等差数列,得2a2=a1+a3-2,
则4q=2+2q2-2,解得q=2(q=0舍去).
则an=a1qn-1=2n,n∈N*.
则数列{bn}的前n项和
探究提高
考向2 裂项相消法求和
(1)求数列{an}与{bn}的通项公式;
解 当n=1时,a1=S1=3.
当n≥2时,an=Sn-Sn-1=n+2.
又a1适合上式,∴an=n+2.
∵b2=a2=4,b3=a6=8,
∴bn=b2·qn-2=4×2n-2=2n(n∈N*).
解 cn=log2bn=n,
1.裂项相消求和就是将数列中的每一项裂成两项或多项,使这些裂开的项出现有规律的相互抵消,要注意消去了哪些项,保留了哪些项.
2.消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.
探究提高
(1)求{an}的通项公式;
得(an+1+an)(an+1-an)=2(an+1+an).
又an>0,知an+1+an≠0,
所以an+1-an=2.
因此数列{an}是首项为1,公差为2的等差数列,
所以an=a1+2(n-1)=2n-1.
解 由(1)知
考向3 错位相减法求和
【例3】 (2021·八省八校一联)已知{an}为等差数列,{bn}为等比数列,{bn}的前n项和为Sn,且a1=b1=1,a2=a3-b3,a3=S3+b2.
(1)求数列{an},{bn}的通项公式;
解 设等差数列{an}的公差为d,等比数列{bn}的公比为q.
∵a1=b1=1,a2=a3-b3,a3=S3+b2,
∴an=4n-3,bn=2n-1.
解 ∵{an}是等差数列,∴an+an+2=2an+1.
又由(1)知bn+2=2bn+1,
①-②,得
1.一般地,如果数列{an}是等差数列,{bn}是等比数列,求数列{an·bn}的前n项和时,可采用错位相减法求和,一般是和式两边同乘以等比数列{bn}的公比,然后作差求解.
2.在写“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”,以便下一步准确地写出“Sn-qSn”的表达式.
探究提高
(1)求数列{an}的通项公式;
解 设等差数列{an}的公差为d,
∴an=2n-1,n∈N*.
(2)若bn=2n-1+1,令cn=an·bn,求数列{cn}的前n项和Tn.
解 由(1)及bn=2n-1+1,得cn=(2n-1)·2n-1+(2n-1),
∴Tn=1×20+3×21+5×22+…+(2n-1)·2n-1+[1+3+…+(2n-1)],
设M=1+3+5+…+(2n-1)=n2,
A=1×20+3×21+5×22+…+(2n-1)·2n-1,
则2A=1×2+3×22+5×23+…+(2n-3)·2n-1+(2n-1)·2n,
两式相减得
∴A=2n(2n-3)+3.
∴Tn=A+M=2n(2n-3)+3+n2.
热点二 an与Sn的关系问题
(1)求数列{an}的通项公式;
解 因为an=5Sn+1,n∈N*,
所以an+1=5Sn+1+1,
(2)求数列{cn}的前n项和An,并求出An的最值.
解 由(1)知bn=-1-log2|an|=2n-1,
数列{bn}的前n项和Tn=n2,
因此{An}是单调递增数列,
1.给出Sn与an的递推关系求an,常用思路是:一是利用Sn-Sn-1=an(n≥2)转化为an的递推关系,再求其通项公式;二是转化为Sn的递推关系,先求出Sn与n之间的关系,再求an.
2.由Sn求an时,一定注意分n=1和n≥2两种情况,最后验证两者是否能合为一个式子,若不能,则用分段形式来表示.
探究提高
(1)求数列{an}的通项公式;
∴数列{an}是等差数列,首项为1,公差为1.
∴an=1+n-1=n.
(2)设bn=(1-an)2-a(1-an),若{bn}是递增数列,求实数a的取值范围.
解 bn=(1-an)2-a(1-an)=(n-1)2+a(n-1),
∵{bn}是递增数列,
∴bn+1-bn=n2+an-(n-1)2-a(n-1)
=2n+a-1>0,
即a>1-2n恒成立,∴a>-1,
∴实数a的取值范围是(-1,+∞).
热点三 与数列相关的综合问题
【例5】 (2021·石家庄质检)已知函数f(x)=logk x(k为常数,k>0且k≠1),且数列{f(an)}是首项为4,公差为2的等差数列.
(1)求证:数列{an}是等比数列;
证明 由题意得f(an)=4+2(n-1)=2n+2,
即logk an=2n+2,所以an=k2n+2,
因为常数k>0且k≠1,所以k2为非零常数,
所以数列{an}是以k4为首项,k2为公比的等比数列.
(3)若cn=anlg an,是否存在k∈(0,1),使得数列{cn}是递增数列,若存在,试求实数k的取值范围;若不存在,说明理由.
解 存在.理由如下:
结合(1)知,cn=anlg an=(2n+2)·k2n+2·lg k,
由{cn}单调递增,即 n∈N*,cn
1.求解数列与函数交汇问题要注意两点:
(1)数列是一类特殊的函数,其定义域是正整数集(或它的有限子集),在求数列最值或不等关系时要特别注意.
(2)解题时准确构造函数,利用函数性质时注意限制条件.
2.本题第(2)问求最值,其实质是利用函数的单调性.第(3)问把{cn}的单调性转化为不等式cn
(1)求数列{an}的通项公式;
解 因为4Sn+1=3Sn-9,
所以当n≥2时,4Sn=3Sn-1-9,
(2)设数列{bn}满足3bn+(n-4)an=0(n∈N*),记{bn}的前n项和为Tn.若Tn≤λbn对任意n∈N*恒成立,求实数λ的取值范围.
解 因为3bn+(n-4)an=0,
当n=4时,-12≤0恒成立;
专题训练 对接高考
3
巩固提升
一、选择题
1.(2021·人大附中调研)在数列{an}中,已知an=n2+λn,n∈N*,则“a1
C.充要条件 D.既不充分也不必要条件
C
解析 若在数列{an}中,已知an=n2+λn,n∈N*,a1
若数列{an}是单调递增数列,则对任意的n∈N*都满足an+1-an=(n+1)2+λ(n+1)-n2-λn=2n+1+λ>0,
∴λ>-1-2n,即λ>(-1-2n)max=-3,
因此,“a1
A.4 B.-4 C.4 040 D.-4 040
解析 因为a4,a4 040是函数f(x)=x2-8x+3的两个零点,即a4,a4 040是方程x2-8x+3=0的两个根,所以a4+a4 040=8.
又2an+1=an+an+2,所以数列{an}是等差数列,
所以a4+a4 040=2a2 022=8,所以a2 022=4.
A
3.在等差数列{an}中,a3+a5=a4+7,a10=19,则数列{ancos nπ}(n∈N*)的前2 022项的和为( )
A.1 011 B.1 010 C.2 022 D.2 020
解析 由题意得a3+a5=2a4=a4+7,解得a4=7,
C
则a1=a4-3d=7-3×2=1,所以an=2n-1,
设bn=ancos nπ,
则b1+b2=a1cos π+a2cos 2π=-a1+a2=2,
b3+b4=a3cos 3π+a4cos 4π=-a3+a4=2,……,
∴数列{ancos nπ}(n∈N*)的前2 022项的和
S2 022=(b1+b2)+(b3+b4)+…+(b2 021+b2 022)=2×1 011=2 022.
A.-16 B.-8 C.8 D.16
解析 当n为奇数时,n+1为偶数,
则an=n2-(n+1)2=-2n-1,
所以a1+a3+a5+a7=-(3+7+11+15)=-36.
当n为偶数时,n+1为奇数,
则an=-n2+(n+1)2=2n+1,
则a2+a4+a6+a8=5+9+13+17=44,
所以a1+a2+a3+…+a8=-36+44=8.
C
解析 由题意,知b1=S2=a1+a2,bn+1=S2n+2-S2n,
可得bn=S2n-S2n-2=a2n+a2n-1(n>1,n∈N*).
由{an}为等差数列,知{bn}为等差数列.
由等差数列的性质,显然A,B成立;
选项C中,a2=a1+d,a4=a1+3d,a8=a1+7d.
D
化简得a1d=d2,
A.a3=13 B.数列{3+an}是等比数列
C.an=4n-3 D.Sn=2n+1-3n
AB
即1+2+2an=an+1,即an+1=3+2an,an+1+3=2(an+3),
所以数列{an+3}是以a1+3=4为首项,2为公比的等比数列,
于是an+3=4×2n-1=2n+1,所以an=2n+1-3,所以a3=24-3=13,所以A,B选项正确,C选项不正确.
又S2=a1+a2=1+5=6,而22+1-3×2=2,所以D选项不正确,故选AB.
99
8.(2021·宿迁质检)已知{an}是公差d不为零的等差数列,a5=14,且a1,a3,a11成等比数列,设bn=(-1)n+1an,数列{bn}的前n项的和为Sn,则S2 021=________.
3 032
解析 由于a1,a3,a11成等比数列,
∴14d2=3a5d.
又d≠0,a5=14,知d=3,
因此an=a5+(n-5)×3=3n-1,bn=(-1)n+1(3n-1).
9.(2021·湖南六校联考)把数列{2n+1}(n∈N*)中的各项依次按第1个括号一个数,第2个括号两个数,第3个括号三个数,第4个括号四个数,第5个括号一个数,…,进行排列,得到如下排列;(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43),…,则第100个括号内各数之和为________.
1 992
解析 把每4个括号算作一组,由题意可知每组共有10个数,则第100个括号为第25组中的最后一个括号,前24组共有240个数,第25组的前3个括号内共有6个数,所以第100个括号内的数是数列{2n+1}的第247,248,249,250项,则第100个括号内的各数之和为(2×247+1+2×250+1)×2=1 992.
三、解答题
问题:是否存在数列{an}(n∈N*),其前n项和为Sn,且a1=1,a3=4,________?
(注:如果选择多个条件分别解答,那么按第一个解答计分.)
所以该数列不存在.
如果选择②an+1=an+d(n∈N*,d为常数),则数列{an}为等差数列,
如果选择③an+1=qan(q>0,n∈N*,q为常数),则数列{an}为等比数列,
(1)求{an}的通项公式;
所以当n=1时,a1=S1=1,
又n=1时符合上式,所以an=n.
b2k+1-b2k-1=(2k+1)-(2k-1)=2,
则{b2k-1}是以1为首项,2为公差的等差数列;
能力突破
12.(多选)(2021·江苏调考)斐波那契螺旋线也称黄金螺旋线,是根据斐波那契数列画出来的螺旋曲线.在一个黄金矩形(宽长比约等于0.618)里先以宽为边长作正方形,然后在剩下小的矩形里以其宽为边长作正方形,如此循环下去,再在每个正方形里画出一段四分之一圆弧,最后顺次连接,就可得到一条“黄金螺旋线”.达·芬奇的《蒙娜丽莎》(如图),希腊雅典卫城的帕特农神庙等都符合这个曲线.现将每一段黄金螺线与其所在的正方形所围成的扇形半径设为an(n∈N*),数列{an}满足a1=a2=1,an=an-1+an-2(n≥3),再将扇形面积设为bn(n∈N*),则( )
ABD
A.4(b2 020-b2 019)=πa2 018a2 021
B.a1+a2+a3+…+a2 019=a2 021-1
C.a+a+a+…+a=2a2 019a2 021
D.a2 019a2 021-a+a2 018a2 020-a=0
因为an=an-1+an-2(n≥3),所以a3=a5-a4,a4=a6-a5,a5=a7-a6,…,a2 018=a2 020-a2 019,a2 019=a2 021-a2 020,又a4=a3+a2=a1+a2+a2=3,所以a1+a2+a3+…+a2 019=a2 021-1,故B正确;
13.(2021·湖北十校一联)已知等差数列{an}与正项等比数列{bn}满足a1=b1=3,且b3-a3,20,a5+b2既是等差数列,又是等比数列.
(1)求数列{an}和{bn}的通项公式;
解 设等差数列{an}的公差为d,等比数列{bn}的公比为q(q>0),
由题意得20=b3-a3=a5+b2,
所以an=2n+1,bn=3n.
选②,cn=anbn=(2n+1)3n,
则Sn=c1+c2+…+cn=3×3+5×32+…+(2n+1)3n,
3Sn=3×32+5×33+…+(2n+1)3n+1,
14.(2021·天津卷)已知{an}是公差为2的等差数列,其前8项和为64.{bn}是公比大于0的等比数列,b1=4,b3-b2=48.
(1)求{an}和{bn}的通项公式;
解 因为{an}是公差为2的等差数列,其前8项和为64,
所以an=a1+2(n-1)=2n-1,n∈N*.
设等比数列{bn}的公比为q(q>0),
所以b3-b2=b1q2-b1q=4(q2-q)=48,解得q=4(负值舍去),
所以bn=b1qn-1=4n ,n∈N*.
同课章节目录
