规范答题示范课——概率与统计解答题(共18张PPT)
文档属性
| 名称 | 规范答题示范课——概率与统计解答题(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 840.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 11:17:26 | ||
图片预览






文档简介
(共18张PPT)
上篇 专题四 概率与统计
规范答题示范课——概率与统计解答题
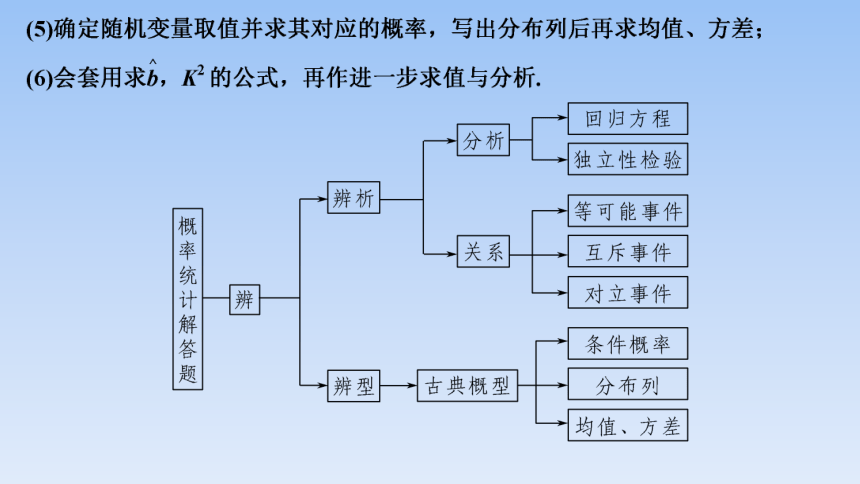
概率与统计问题需要从数据中获取有用的信息,通过数据的筛选、分析构建相关模型特别是从图表、直方图中获取信息,利用图表信息进行数据分析.
解题的关键是“辨”——辨析、辨型,求解要抓住几点:
(1)准确弄清问题所涉及的事件有什么特点,事件之间有什么关系,如互斥、对立、独立等;
(2)理清事件以什么形式发生,如同时发生、至少有几个发生、至多有几个发生、恰有几个发生等;
(3)明确抽取方式,是放回还是不放回、抽取有无顺序等;
(4)准确选择排列组合的方法来计算基本事件发生数和事件总数,或根据概率计算公式和性质来计算事件的概率;
(12分)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列.
解 X的所有可能取值为-1,0,1. 1分
P(X=-1)=(1-α)β,
P(X=0)=αβ+(1-α)(1-β),
P(X=1)=α(1-β), 3分
所以X的分布列为
X -1 0 1
P (1-α)β αβ+(1-α)(1-β) α(1-β)
4分
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
①证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
②求p4,并根据p4的值解释这种试验方案的合理性.
①证明 由(1)得a=0.4,b=0.5,c=0.1,
因此pi=0.4pi-1+0.5pi+0.1pi+1,
故0.1(pi+1-pi)=0.4(pi-pi-1),
则pi+1-pi=4(pi-pi-1). 6分
又因为p1-p0=p1≠0,
所以{pi+1-pi}(i=0,1,2,…,7)是公比为4,首项为p1的等比数列. 8分
得步骤分:对于解题过程中是得分点的步骤,有则给分,无则没分,所以对于得分点步骤一定要写全.如第(1)问中,写出随机变量X的可能取值,第(2)问中说明{pi+1-pi}的公比,首项,利用p4的值说明最后的结论合理性等.
得关键分:对于解题过程中的关键点,有则给分,无则没分,所以在答题时一定要写清得分关键点,如第(1)问分布列必须用表格表示,第(2)问中pi+1-pi=4(pi-pi-1)的关系式及条件p1-p0=p1≠0,否则都会导致扣分.
得计算分:如第(2)问中累加求p8与p1的关系,由p8求p1,p4的值,若出错,会每次扣去1分.
1.(2021·徐州检测)已知6只小白鼠中有且仅有2只患有某种疾病,需要通过化验血液来确定患病的小白鼠.血液化验呈阳性即为患病,阴性为不患病.现将6只小白鼠随机排序并化验血液,每次测1只,且得到前一只小白鼠的血液化验结果之后才化验下一只小白鼠的血液,直到能确定哪两只小白鼠患病为止,并用X表示化验总次数.
(1)在第一只小白鼠验血结果为阳性的条件下,求X=3的概率;
(2)求X的分布列与数学期望.
解 X的可能取值为2,3,4,5.
故X的分布列为
2.(2021·八省八校一联)国家发展改革委、住房城乡建设部于2017年发布了《生活垃圾分类制度实施方案》,规定46个城市在2020年底实施生活垃圾强制分类,垃圾回收、利用率要达35%以上.截至2019年底,这46个重点城市生活垃圾分类的居民小区覆盖率已经接近70%.武汉市在实施垃圾分类之前,从本市人口数量在两万人左右的320个社区中随机抽取50个社区,对这50个社区某天产生的垃圾量(单位:吨)进行了调查,得到如下频数分布表,并将人口数量在两万人左右的社区垃圾量超过28吨/天的确定为“超标”社区.
垃圾量x/吨 [12.5,15.5) [15.5,18.5) [18.5,21.5) [21.5,24.5) [24.5,27.5) [27.5,30.5) [30.5,33.5]
频数 5 6 9 12 8 6 4
解 由频数分布表得
估计这50个社区这一天垃圾量的平均值为22.8吨.
解 由(1)知μ≈22.8.∵s≈5.2,σ≈s≈5.2,
∵320×0.158 65=50.768≈51,
∴估计这320个社区中“超标”社区的个数为51.
(3)通过研究样本原始数据发现,抽取的50个社区中这一天共有8个“超标”社区,市政府决定对这8个“超标”社区的垃圾来源进行跟踪调查.现计划在这8个“超标”社区中任取5个先进行跟踪调查,设Y为抽到的这一天的垃圾量至少为30.5吨的社区个数,求Y的分布列与数学期望.
[参考数据:P(μ-σ解 由频率分布表知,8个“超标”社区中这一天的垃圾量至少为30.5吨的社区有4个,
∴Y的所有可能取值为1,2,3,4,
∴Y的分布列为
上篇 专题四 概率与统计
规范答题示范课——概率与统计解答题
概率与统计问题需要从数据中获取有用的信息,通过数据的筛选、分析构建相关模型特别是从图表、直方图中获取信息,利用图表信息进行数据分析.
解题的关键是“辨”——辨析、辨型,求解要抓住几点:
(1)准确弄清问题所涉及的事件有什么特点,事件之间有什么关系,如互斥、对立、独立等;
(2)理清事件以什么形式发生,如同时发生、至少有几个发生、至多有几个发生、恰有几个发生等;
(3)明确抽取方式,是放回还是不放回、抽取有无顺序等;
(4)准确选择排列组合的方法来计算基本事件发生数和事件总数,或根据概率计算公式和性质来计算事件的概率;
(12分)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列.
解 X的所有可能取值为-1,0,1. 1分
P(X=-1)=(1-α)β,
P(X=0)=αβ+(1-α)(1-β),
P(X=1)=α(1-β), 3分
所以X的分布列为
X -1 0 1
P (1-α)β αβ+(1-α)(1-β) α(1-β)
4分
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
①证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
②求p4,并根据p4的值解释这种试验方案的合理性.
①证明 由(1)得a=0.4,b=0.5,c=0.1,
因此pi=0.4pi-1+0.5pi+0.1pi+1,
故0.1(pi+1-pi)=0.4(pi-pi-1),
则pi+1-pi=4(pi-pi-1). 6分
又因为p1-p0=p1≠0,
所以{pi+1-pi}(i=0,1,2,…,7)是公比为4,首项为p1的等比数列. 8分
得步骤分:对于解题过程中是得分点的步骤,有则给分,无则没分,所以对于得分点步骤一定要写全.如第(1)问中,写出随机变量X的可能取值,第(2)问中说明{pi+1-pi}的公比,首项,利用p4的值说明最后的结论合理性等.
得关键分:对于解题过程中的关键点,有则给分,无则没分,所以在答题时一定要写清得分关键点,如第(1)问分布列必须用表格表示,第(2)问中pi+1-pi=4(pi-pi-1)的关系式及条件p1-p0=p1≠0,否则都会导致扣分.
得计算分:如第(2)问中累加求p8与p1的关系,由p8求p1,p4的值,若出错,会每次扣去1分.
1.(2021·徐州检测)已知6只小白鼠中有且仅有2只患有某种疾病,需要通过化验血液来确定患病的小白鼠.血液化验呈阳性即为患病,阴性为不患病.现将6只小白鼠随机排序并化验血液,每次测1只,且得到前一只小白鼠的血液化验结果之后才化验下一只小白鼠的血液,直到能确定哪两只小白鼠患病为止,并用X表示化验总次数.
(1)在第一只小白鼠验血结果为阳性的条件下,求X=3的概率;
(2)求X的分布列与数学期望.
解 X的可能取值为2,3,4,5.
故X的分布列为
2.(2021·八省八校一联)国家发展改革委、住房城乡建设部于2017年发布了《生活垃圾分类制度实施方案》,规定46个城市在2020年底实施生活垃圾强制分类,垃圾回收、利用率要达35%以上.截至2019年底,这46个重点城市生活垃圾分类的居民小区覆盖率已经接近70%.武汉市在实施垃圾分类之前,从本市人口数量在两万人左右的320个社区中随机抽取50个社区,对这50个社区某天产生的垃圾量(单位:吨)进行了调查,得到如下频数分布表,并将人口数量在两万人左右的社区垃圾量超过28吨/天的确定为“超标”社区.
垃圾量x/吨 [12.5,15.5) [15.5,18.5) [18.5,21.5) [21.5,24.5) [24.5,27.5) [27.5,30.5) [30.5,33.5]
频数 5 6 9 12 8 6 4
解 由频数分布表得
估计这50个社区这一天垃圾量的平均值为22.8吨.
解 由(1)知μ≈22.8.∵s≈5.2,σ≈s≈5.2,
∵320×0.158 65=50.768≈51,
∴估计这320个社区中“超标”社区的个数为51.
(3)通过研究样本原始数据发现,抽取的50个社区中这一天共有8个“超标”社区,市政府决定对这8个“超标”社区的垃圾来源进行跟踪调查.现计划在这8个“超标”社区中任取5个先进行跟踪调查,设Y为抽到的这一天的垃圾量至少为30.5吨的社区个数,求Y的分布列与数学期望.
[参考数据:P(μ-σ
∴Y的所有可能取值为1,2,3,4,
∴Y的分布列为
同课章节目录
