拓展优化 概率与统计的综合创新(共20张PPT)
文档属性
| 名称 | 拓展优化 概率与统计的综合创新(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 687.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 11:18:02 | ||
图片预览





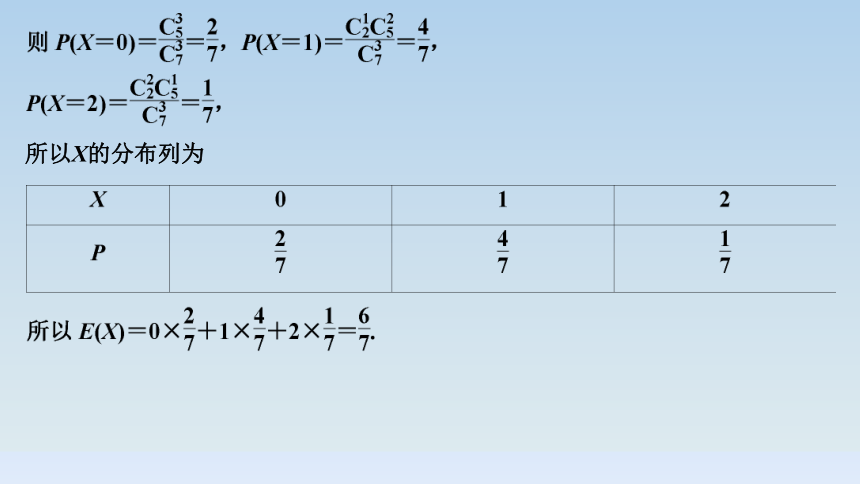
文档简介
(共20张PPT)
上篇 专题四 概率与统计
拓展优化 概率与统计的综合创新
随着新课程的推进改革,概率与统计命题情境新颖、综合性强,综合考查学生数学建模、数据分析与数学运算等数学素养,掌握该类问题的解题策略愈加重要.
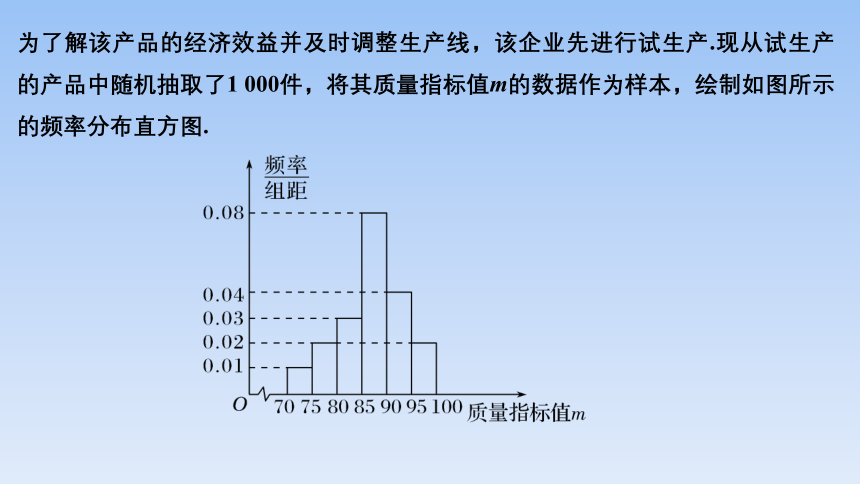
【典例1】 2020年10月16日是第40个世界粮食日.与此同时,中国工程院院士袁隆平海水稻团队完成了10万亩海水稻的测产收割,其中宁夏石嘴山海水稻示范种植基地编号为YC801的水稻亩产超过648.5千克.推广种植海水稻,能实现亿亩荒滩变粮仓,大大提高当地居民收入.某企业引进一条先进食品生产线,以海水稻为原料进行深加工,发明了一种新产品,若该产品的质量指标值为m(m∈[70,100]),其质量指标等级划分如下表:
质量指标值m [70,75) [75,80) [80,85) [85,90) [90,100]
质量指标等级 良好 优秀 良好 合格 废品
为了解该产品的经济效益并及时调整生产线,该企业先进行试生产.现从试生产的产品中随机抽取了1 000件,将其质量指标值m的数据作为样本,绘制如图所示的频率分布直方图.
(1)若将频率作为概率,从该产品中随机抽取3件产品,记“抽出的产品中至少有1件不是废品”为事件A,求事件A发生的概率;
(2)若从质量指标值m不低于85的样本中利用分层抽样的方法抽取7件产品,然后从这7件产品中任取3件产品,求质量指标值m∈[90,95)的件数X的分布列及数学期望;
解 由频率分布直方图可知,质量指标值不低于85的产品中,
m∈[85,90)的频率为0.08×5=0.4;
m∈[90,95)的频率为0.04×5=0.2;
m∈[95,100]的频率为0.02×5=0.1.
故利用分层抽样的方法抽取的7件产品中,m∈[85,90)的有4件,m∈[90,95)的有2件,m∈[95,100]的有1件.
从这7件产品中任取3件产品,质量指标值m∈[90,95)的件数X的所有可能取值为0,1,2,
所以X的分布列为
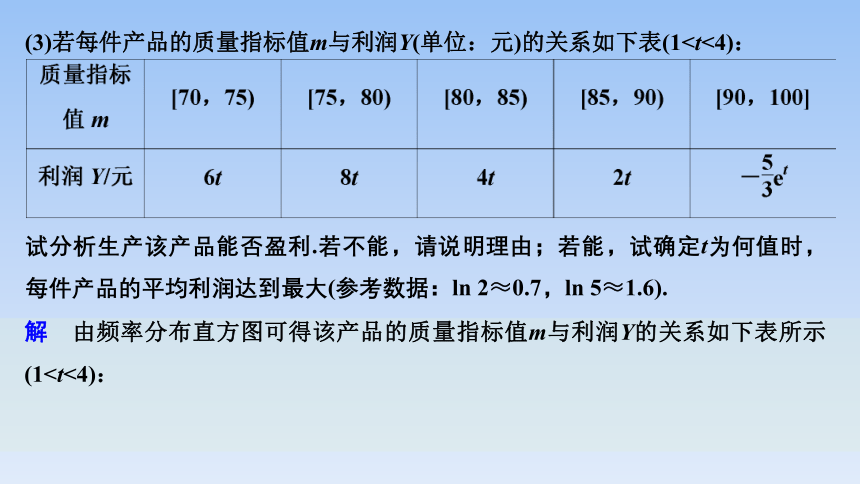
(3)若每件产品的质量指标值m与利润Y(单位:元)的关系如下表(1试分析生产该产品能否盈利.若不能,请说明理由;若能,试确定t为何值时,每件产品的平均利润达到最大(参考数据:ln 2≈0.7,ln 5≈1.6).
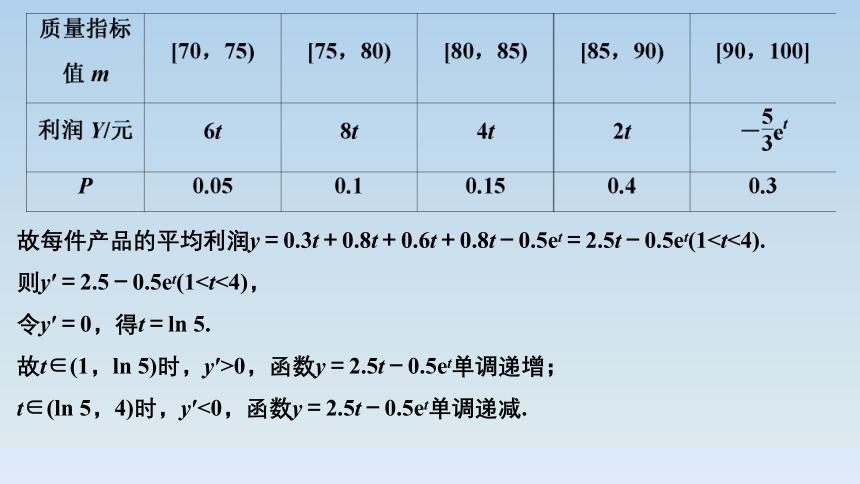
解 由频率分布直方图可得该产品的质量指标值m与利润Y的关系如下表所示(1故每件产品的平均利润y=0.3t+0.8t+0.6t+0.8t-0.5et=2.5t-0.5et(1则y′=2.5-0.5et(1令y′=0,得t=ln 5.
故t∈(1,ln 5)时,y′>0,函数y=2.5t-0.5et单调递增;
t∈(ln 5,4)时,y′<0,函数y=2.5t-0.5et单调递减.
所以当t=ln 5时,y取得最大值,为2.5×ln 5-0.5eln 5≈1.5>0.
所以生产该产品能够盈利,当t=ln 5≈1.6时,每件产品的平均利润取得最大值1.5元.
1.本题以“粮食安全”为背景考查统计与概率、随机变量及概率分布、函数与导数等知识,意在考查数学建模、数据分析与数学运算等核心素养.
2.解题的突破口是读懂题意,提炼图表信息,盯住题眼,构建概率分布及函数模型.
点津突破
【典例2】 甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n次这样的操作,记甲口袋中黑球个数为Xn,恰有2个黑球的概率为pn,恰有1个黑球的概率为qn.
(1)求p1,q1和p2,q2;
(2)求2pn+qn与2pn-1+qn-1的递推关系式和Xn的数学期望E(Xn)(用n表示).
Xn的概率分布为
Xn 0 1 2
P 1-pn-qn qn pn
[跟踪演练]
一种掷骰子走跳棋的游戏:棋盘上标有第0站、第1站、第2站,…,第100站,共101站,设棋子跳到第n站的概率为Pn,一枚棋子开始在第0站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数1,2,3,4,5,6).
(1)求P0,P1,P2,并根据棋子跳到第n站的情况,试用Pn-2和Pn-1表示Pn;
(2)求证:{Pn-Pn-1}(n=1,2,…,99)为等比数列;
(3)求玩该游戏获胜的概率.
解 由(2)知,
上篇 专题四 概率与统计
拓展优化 概率与统计的综合创新
随着新课程的推进改革,概率与统计命题情境新颖、综合性强,综合考查学生数学建模、数据分析与数学运算等数学素养,掌握该类问题的解题策略愈加重要.
【典例1】 2020年10月16日是第40个世界粮食日.与此同时,中国工程院院士袁隆平海水稻团队完成了10万亩海水稻的测产收割,其中宁夏石嘴山海水稻示范种植基地编号为YC801的水稻亩产超过648.5千克.推广种植海水稻,能实现亿亩荒滩变粮仓,大大提高当地居民收入.某企业引进一条先进食品生产线,以海水稻为原料进行深加工,发明了一种新产品,若该产品的质量指标值为m(m∈[70,100]),其质量指标等级划分如下表:
质量指标值m [70,75) [75,80) [80,85) [85,90) [90,100]
质量指标等级 良好 优秀 良好 合格 废品
为了解该产品的经济效益并及时调整生产线,该企业先进行试生产.现从试生产的产品中随机抽取了1 000件,将其质量指标值m的数据作为样本,绘制如图所示的频率分布直方图.
(1)若将频率作为概率,从该产品中随机抽取3件产品,记“抽出的产品中至少有1件不是废品”为事件A,求事件A发生的概率;
(2)若从质量指标值m不低于85的样本中利用分层抽样的方法抽取7件产品,然后从这7件产品中任取3件产品,求质量指标值m∈[90,95)的件数X的分布列及数学期望;
解 由频率分布直方图可知,质量指标值不低于85的产品中,
m∈[85,90)的频率为0.08×5=0.4;
m∈[90,95)的频率为0.04×5=0.2;
m∈[95,100]的频率为0.02×5=0.1.
故利用分层抽样的方法抽取的7件产品中,m∈[85,90)的有4件,m∈[90,95)的有2件,m∈[95,100]的有1件.
从这7件产品中任取3件产品,质量指标值m∈[90,95)的件数X的所有可能取值为0,1,2,
所以X的分布列为
(3)若每件产品的质量指标值m与利润Y(单位:元)的关系如下表(1
解 由频率分布直方图可得该产品的质量指标值m与利润Y的关系如下表所示(1
故t∈(1,ln 5)时,y′>0,函数y=2.5t-0.5et单调递增;
t∈(ln 5,4)时,y′<0,函数y=2.5t-0.5et单调递减.
所以当t=ln 5时,y取得最大值,为2.5×ln 5-0.5eln 5≈1.5>0.
所以生产该产品能够盈利,当t=ln 5≈1.6时,每件产品的平均利润取得最大值1.5元.
1.本题以“粮食安全”为背景考查统计与概率、随机变量及概率分布、函数与导数等知识,意在考查数学建模、数据分析与数学运算等核心素养.
2.解题的突破口是读懂题意,提炼图表信息,盯住题眼,构建概率分布及函数模型.
点津突破
【典例2】 甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n次这样的操作,记甲口袋中黑球个数为Xn,恰有2个黑球的概率为pn,恰有1个黑球的概率为qn.
(1)求p1,q1和p2,q2;
(2)求2pn+qn与2pn-1+qn-1的递推关系式和Xn的数学期望E(Xn)(用n表示).
Xn的概率分布为
Xn 0 1 2
P 1-pn-qn qn pn
[跟踪演练]
一种掷骰子走跳棋的游戏:棋盘上标有第0站、第1站、第2站,…,第100站,共101站,设棋子跳到第n站的概率为Pn,一枚棋子开始在第0站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数1,2,3,4,5,6).
(1)求P0,P1,P2,并根据棋子跳到第n站的情况,试用Pn-2和Pn-1表示Pn;
(2)求证:{Pn-Pn-1}(n=1,2,…,99)为等比数列;
(3)求玩该游戏获胜的概率.
解 由(2)知,
同课章节目录
