规范答题示范课——解析几何解答题(共17张PPT)
文档属性
| 名称 | 规范答题示范课——解析几何解答题(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 722.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 11:19:41 | ||
图片预览




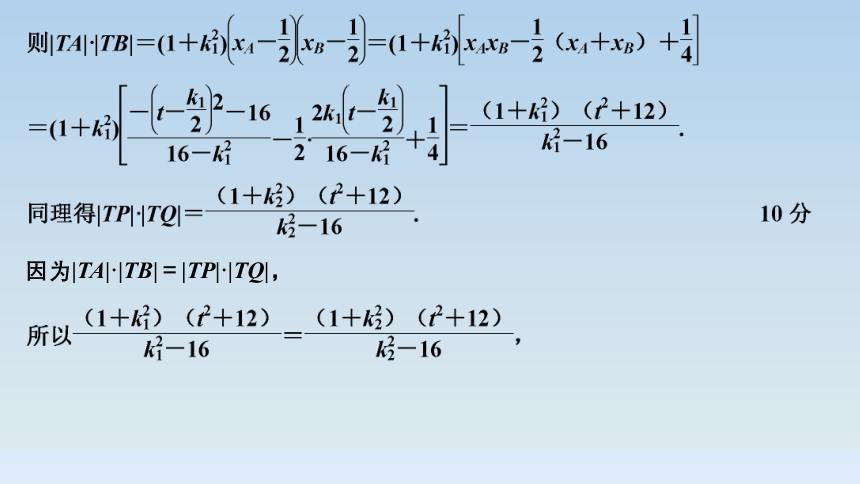

文档简介
(共17张PPT)
上篇 专题五 解析几何
规范答题示范课——解析几何解答题
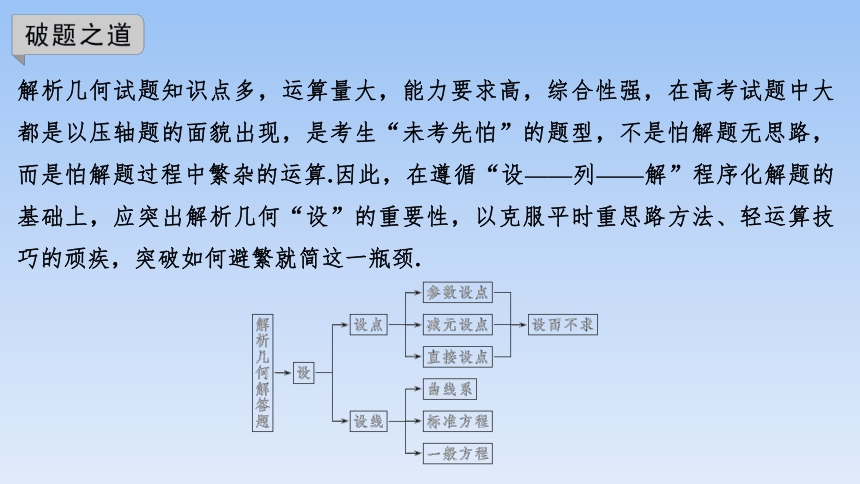
解析几何试题知识点多,运算量大,能力要求高,综合性强,在高考试题中大都是以压轴题的面貌出现,是考生“未考先怕”的题型,不是怕解题无思路,而是怕解题过程中繁杂的运算.因此,在遵循“设——列——解”程序化解题的基础上,应突出解析几何“设”的重要性,以克服平时重思路方法、轻运算技巧的顽疾,突破如何避繁就简这一瓶颈.
因为|TA|·|TB|=|TP|·|TQ|,
又k1≠k2,所以k1=-k2,即k1+k2=0.
故直线AB的斜率与直线PQ的斜率之和为0. 12分
(1)求C的方程;
(2)若点P在C上,点Q在直线x=6上,且|BP|=|BQ|,BP⊥BQ,求△APQ的面积.
解 设P(xP,yP),Q(6,yQ),根据对称性可设yQ>0,
由题意知yP>0.
因为|BP|=|BQ|,所以yP=1.
将yP=1代入C的方程,解得xP=3或-3.
由直线BP的方程得yQ=2或8,
所以点P,Q的坐标分别为P1(3,1),Q1(6,2)或P2(-3,1),Q2(6,8),
(1)求椭圆C的方程;
证明 由(1)得,曲线为x2+y2=1(x>0),
当直线MN的斜率不存在时,直线MN的方程为x=1,显然不合题意;
当直线MN的斜率存在时,设M(x1,y1),N(x2,y2).
必要性:
所以必要性成立;
充分性:设直线MN:y=kx+m(km<0),即kx-y+m=0,
其中Δ=(6km)2-4(1+3k2)(3m2-3)=24k2>0,
上篇 专题五 解析几何
规范答题示范课——解析几何解答题
解析几何试题知识点多,运算量大,能力要求高,综合性强,在高考试题中大都是以压轴题的面貌出现,是考生“未考先怕”的题型,不是怕解题无思路,而是怕解题过程中繁杂的运算.因此,在遵循“设——列——解”程序化解题的基础上,应突出解析几何“设”的重要性,以克服平时重思路方法、轻运算技巧的顽疾,突破如何避繁就简这一瓶颈.
因为|TA|·|TB|=|TP|·|TQ|,
又k1≠k2,所以k1=-k2,即k1+k2=0.
故直线AB的斜率与直线PQ的斜率之和为0. 12分
(1)求C的方程;
(2)若点P在C上,点Q在直线x=6上,且|BP|=|BQ|,BP⊥BQ,求△APQ的面积.
解 设P(xP,yP),Q(6,yQ),根据对称性可设yQ>0,
由题意知yP>0.
因为|BP|=|BQ|,所以yP=1.
将yP=1代入C的方程,解得xP=3或-3.
由直线BP的方程得yQ=2或8,
所以点P,Q的坐标分别为P1(3,1),Q1(6,2)或P2(-3,1),Q2(6,8),
(1)求椭圆C的方程;
证明 由(1)得,曲线为x2+y2=1(x>0),
当直线MN的斜率不存在时,直线MN的方程为x=1,显然不合题意;
当直线MN的斜率存在时,设M(x1,y1),N(x2,y2).
必要性:
所以必要性成立;
充分性:设直线MN:y=kx+m(km<0),即kx-y+m=0,
其中Δ=(6km)2-4(1+3k2)(3m2-3)=24k2>0,
同课章节目录
