第2讲 基本初等函数、函数的应用 课件(共75张PPT)
文档属性
| 名称 | 第2讲 基本初等函数、函数的应用 课件(共75张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 22:34:30 | ||
图片预览











文档简介
(共75张PPT)
上篇 专题六 函数与导数
第2讲 基本初等函数、函数的应用
高考定位
1.掌握二次函数、分段函数、幂函数、指数函数、对数函数的图象与性质;2.以基本初等函数为依托,考查函数与方程的关系、函数零点存在性定理;3.能利用函数解决简单的实际问题.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
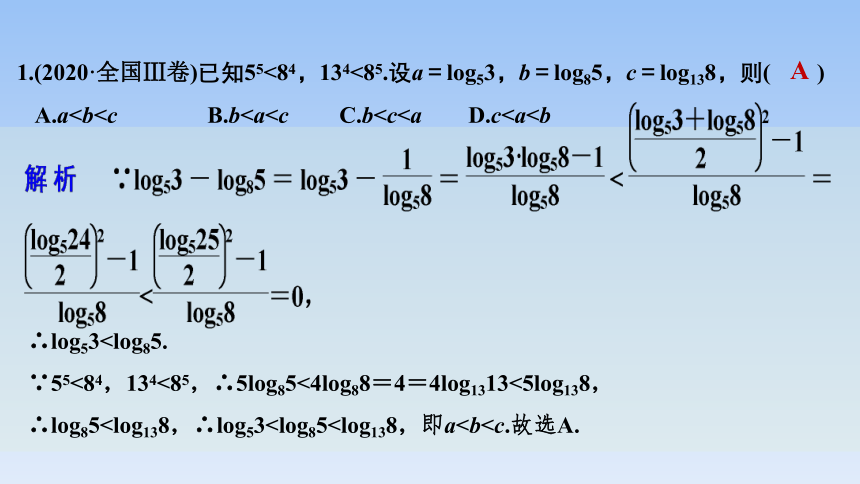
1.(2020·全国Ⅲ卷)已知55<84,134<85.设a=log53,b=log85,c=log138,则( )
A.aA
∴log53∵55<84,134<85,∴5log85<4log88=4=4log1313<5log138,
∴log852.(2020·全国Ⅱ卷)若2x-2y<3-x-3-y,则( )
A.ln(y-x+1)>0 B.ln(y-x+1)<0
C.ln|x-y|>0 D.ln|x-y|<0
解析 设函数f(x)=2x-3-x.
因为函数y=2x与y=-3-x在R上均单调递增,
所以f(x)在R上单调递增.
原已知条件等价于2x-3-x<2y-3-y,
即f(x)0,y-x+1>1,所以A正确,B不正确.
因为|x-y|与1的大小不能确定,所以C,D不正确.
A
解析 因为x2-2(a+1)x+a2+5=0最多有2个根,
所以cos (2πx-2πa)=0至少有4个根.
A
②当x≥a时,f(x)=x2-2(a+1)x+a2+5,
Δ=4(a+1)2-4(a2+5)=8(a-2),
当a<2时,Δ<0,f(x)无零点;
当a=2时,Δ=0,f(x)有1个零点x=3;
当a>2时,令f(a)=a2-2a(a+1)+a2+5=-2a+5≥0,则2<a≤,此时f(x)有2个零点;
4.(2021·北京卷)已知f(x)=|lg x|-kx-2,给出下列四个结论:
(1)若k=0,则f(x)有两个零点;
(2) k<0,使得f(x)有一个零点;
(3) k<0,使得f(x)有三个零点;
(4) k>0,使得f(x)有三个零点.
以上正确结论的序号是________.
(1)(2)(4)
解析 令f(x)=|lg x|-kx-2=0,
可转化成两个函数y1=|lg x|,y2=kx+2的图象的交点个数问题.
对于(1),当k=0时,y2=2与y1=|lg x|的图象有两个交点,(1)正确;
对于(2),存在k<0,使y2=kx+2与y1=|lg x|的图象相切,(2)正确;
对于(3),若k<0,则y1=|lg x|与y2=kx+2的图象最多有2个交点,(3)错误;
对于(4),当k>0时,过点(0,2)存在函数g(x)=lg x(x>1)图象的切线,此时共有两个交点,当直线斜率稍微小于相切时的斜率时,就会有3个交点,故(4)正确.
1.指数式与对数式的七个运算公式
2.指数函数与对数函数的图象和性质
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图象和性质,分01两种情况,当a>1时,两函数在定义域内都为增函数,当03.函数的零点问题
(1)函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.
(2)确定函数零点的常用方法:①直接解方程法;②利用零点存在性定理;③数形结合,利用两个函数图象的交点求解.
4.应用函数模型解决实际问题的一般程序
2
热点聚焦 分类突破
热点一 基本初等函数的图象与性质
【例1】 (1)(多选)(2021·八省八校一联)下列命题中正确的是( )
ABC
D
解析 y=logax的图象关于y轴对称的图象对应的函数为y=loga(-x),函数f(x)的图象上有且仅有两个点关于y轴对称,等价于y=loga(-x)与y=|x+2|,-3≤x≤0的图象有且仅有一个交点.
当0<a<1时,显然符合题意(图略).
当a>1时,只需loga3>1,∴1<a<3.
综上所述,a的取值范围是(0,1)∪(1,3).
1.指数函数、对数函数的图象和性质受底数a的影响,解决与指数、对数函数特别是与单调性有关的问题时,首先要看底数a的范围.
2.基本初等函数的图象和性质是统一的,在解题中可相互转化.
探究提高
解析 易知f(x)在定义域R上为非奇非偶函数,B不合题意.
当x<0且x→-∞时,f(x)>0,且f(x)→+∞,C不合题意.
当x>0且x→+∞时,f(x)→0,知D不合题意,只有A满足.
A
(2)(多选)(2021·南京、盐城一模)已知函数f(x)=log2(1+4x)-x,则下列说法正确的是( )
A.函数f(x)是偶函数 B.函数f(x)是奇函数
C.函数f(x)在(-∞,0]上单调递增 D.函数f(x)的值域为[1,+∞)
AD
所以函数f(x)为偶函数,故A正确,B不正确;
则当x<0时,f′(x)<0,函数f(x)单调递减,当x>0时,f′(x)>0,函数f(x)单调递增,故C不正确;
由以上分析知,f(x)min=f(0)=1,
所以函数f(x)的值域为[1,+∞),故D正确.综上所述,选AD.
热点二 函数的零点与方程
考向1 确定函数零点个数
【例2】 (1)(2021·大连调研)设函数f(x)=2|x|+x2-3,则函数y=f(x)的零点个数是( )
A.4 B.3 C.2 D.1
C
解析 易知f(x)是偶函数,当x≥0时,f(x)=2x+x2-3,所以x≥0时,f(x)在[0,+∞)上是增函数,且f(1)=0,所以x=1是函数y=f(x)在[0,+∞)上的唯一零点.
根据奇偶性,知x=-1是y=f(x)在(-∞,0)内的零点,
因此y=f(x)有两个零点.
解析 当x≥0时,f(x)=4x3-6x2+1的导数为f′(x)=12x2-12x,
当0<x<1时,f(x)单调递减,x>1时,f(x)单调递增,
A
可得f(x)在x=1处取得最小值,最小值为-1,且f(0)=1,
作出函数f(x)的图象,如图.
g(x)=3[f(x)]2-10f(x)+3,
可令g(x)=0,t=f(x),可得3t2-10t+3=0,
即g(x)有三个零点;
当t=3时,可得f(x)=3有一个实根,即g(x)有一个零点.
综上,g(x)共有四个零点.
判断函数零点个数的主要方法
(1)解方程f(x)=0,直接求零点;(2)利用零点存在性定理;
(3)数形结合法:对于给定的函数不能直接求解或画出图象,常会通过分解转化为两个能画出图象的函数,求其图象交点问题.
探究提高
【训练2】 (1)函数f(x)=2sin x-sin 2x在[0,2π]的零点个数为( )
A.2 B.3 C.4 D.5
B
解析 令f(x)=0,得2sin x-sin 2x=0,
即2sin x-2sin xcos x=0,
∴2sin x(1-cos x)=0,∴sin x=0或cos x=1.
又x∈[0,2π],
∴由sin x=0得x=0,π或2π,由cos x=1得x=0或2π.
故函数f(x)的零点为0,π,2π,共3个.
解析 对于任意的x∈R,都有f(2+x)=f(2-x),
∴f(x+4)=f[2+(x+2)]=f[2-(x+2)]=f(-x)=f(x),
∴函数f(x)是一个周期函数,且T=4.
C
则函数y=f(x)与y=log8(x+2)在区间(-2,6)上的图象如图所示,
根据图象可得y=f(x)与y=log8(x+2)在区间(-2,6)上有3个不同的交点,即f(x)-log8(x+2)=0在区间(-2,6)上有3个根.
考向2 根据函数的零点求参数的值或范围
【例3】 (1)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=( )
C
解析 f(x)=(x-1)2+a(ex-1+e1-x)-1,
令t=x-1,则g(t)=f(t+1)=t2+a(et+e-t)-1.
∵g(-t)=(-t)2+a(e-t+et)-1=g(t),且t∈R,
∴函数g(t)为偶函数.
∵f(x)有唯一零点,∴g(t)也有唯一零点.
又g(t)为偶函数,由偶函数的性质知g(0)=0,
解析 由题意,令y=f(x)-ax-b=0,得
C
则以上两个函数的图象恰有3个交点,根据选项进行讨论.
①当a<-1时,1-a>0,可知在x∈(-∞,0)上,g(x)单调递增,且g(x)<0;
由g′(x)=x2-(a+1)x=x[x-(a+1)](x≥0),a+1<0,
可知在x∈[0,+∞)上,g(x)单调递增,且g(x)≥0.
此时直线y=b与g(x)的图象只有1个交点,不符合题意,故排除A,B.
②当a>-1,即a+1>0时.
因为g′(x)=x[x-(a+1)](x≥0),所以当x≥0时,
由g′(x)<0可得00可得x>a+1,
所以当x≥0时,g(x)在(0,a+1)上单调递减,g(x)在(a+1,+∞)上单调递增.
如图,y=b与y=g(x)(x≥0)的图象至多有2个交点.
当1-a>0,即-1当1-a=0时,y=g(x)与y=b的图象可以有1个、2个或无数个交点,但不存在恰有3个交点的情况,不符合题意,舍去;
当1-a<0,即a>1时,y=g(x)与y=b的图象可以有1个或2个交点,但不存在恰有3个交点的情况,不符合题意,舍去.
综上,-11.求解第(1)题关键是利用函数f(x)有唯一零点找到解题思路.借助换元法,构造函数g(t)=f(t+1)=t2+a(et+e-t)-1,利用函数的性质求解.
2.解决由函数零点的存在情况求参数的值或取值范围问题,关键是利用函数方程思想或数形结合思想,构建关于参数的方程或不等式求解.
探究提高
【训练3】 设函数f(x)=ex(2x-1)-ax+a(a<1)有两个零点,则实数a的取值范围是( )
A
解析 依题设,f(x)=ex(2x-1)-ax+a有两个零点,
∴函数y=ex(2x-1)的图象与直线y=a(x-1)有两个交点.
设直线y=a(x-1)与y=ex(2x-1)相切于点P(x0,y0),
∴y0=ex0(2x0-1).
则过点P(x0,y0)的切线为
y-ex0(2x0-1)=ex0(2x0+1)(x-x0).
此时,直线y=a(x-1)的斜率为1.
故若直线y=a(x-1)与函数y=ex(2x-1)的图象有两个交点,应有0热点三 函数的实际应用
(1)求桥AB的长度;
解 如图,设AA1,BB1,CD1,EF1都与MN垂直,A1,B1,D1,F1是相应垂足.
由条件知,当O′B=40时,
得O′A=80.
所以AB=O′A+O′B=80+40=120(米).
解 以O为原点,OO′所在直线为y轴建立平面直角坐标系xOy(如图所示).
因为CE=80,所以O′C=80-x.
记桥墩CD和EF的总造价为f(x)万元,
令f′(x)=0,得x=20或x=0(舍去).
列表如下:
X (0,20) 20 (20,40)
f′(x) - 0 +
f(x) ? 极小值 ?
所以当x=20时,f(x)取得最小值.
答:(1)桥AB的长度为120米;
(2)当O′E为20米时,桥墩CD与EF的总造价最低.
1.解决函数的实际应用问题时,首先要耐心、细心地审清题意,弄清各量之间的关系,再建立函数关系式,然后借助函数的知识求解,解答后再回到实际问题中去.
2.对函数模型求最值的常用方法:单调性法、基本不等式法及导数法.
探究提高
【训练4】 (2021·西南名校联考)“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=eax+b(a,b为常数),若该果蔬在6 ℃的保鲜时间为216小时,在24 ℃的保鲜时间为8小时,且该果蔬所需物流时间为3天,则物流过程中果蔬的储藏温度(假设物流过程中恒温)最高不能超过( )
A.9 ℃ B.12 ℃ C.18 ℃ D.20 ℃
B
解析 当x=6时,e6a+b=216;当x=24时,e24a+b=8,
故物流过程中果蔬的储藏温度最高不能超过12 ℃.
专题训练 对接高考
3
巩固提升
A.a<b<c B.c<a<b C.b<c<a D.a<c<b
D
解析 ∵log20.3<log21=0,∴a<0.
∵0<0.40.3<0.40=1,∴0<c<1,
∴a<c<b.
A.2 B.3 C.4 D.5
解析 由f(x+1)=-f(x),得f(x+2)=f(x),知周期T=2.
令f(x)-|x|=0,得f(x)=|x|.
作出函数y=f(x)与g(x)=|x|的图象如图所示.
A
由图象知,函数y=f(x)-|x|有两个零点.
A.60 B.63 C.66 D.69
C
B
所以g(x)在(0,1)上必然存在零点,
即x0∈(0,1),
因此f(x0)=[x0]=0,
所以g[f(x0)]=g(0)=-2.
5.(多选)(2021·江苏调考)若0b>1,则( )
A.logac>logbc B.abc>bac
C.alogbc>blogac D.a(b-c)>b(a-c)
AB
所以0>logac>logbc,故A正确;
对于B,因为01时,函数y=xc-1单调递减,
所以bc-1>ac-1,又ab>0,所以由不等式的基本性质得abc>bac,故B正确;
对于C,由A知logbcb>1,所以alogbc对于D,因为0b>1,所以ac>bc,所以-ac<-bc,所以ab-ac6.(多选)(2021·湖南六校联考)已知f(x)是定义在R上的奇函数,且f(1+x)=f(1-x),当0≤x≤1时,f(x)=x,则关于函数g(x)=|f(x)|+f(|x|),下列说法正确的是( )
A.g(x)为偶函数 B.g(x)在(1,2)上单调递增
C.g(x)在[2 016,2 020]上恰有三个零点 D.g(x)的最大值为2
AD
解析 易知函数g(x)的定义域为R,
且g(-x)=|f(-x)|+f(|-x|)=|-f(x)|+f(|x|)=|f(x)|+f(|x|)=g(x),
所以g(x)为偶函数,故A正确;
因为f(1+x)=f(1-x),所以f(x)的图象关于直线x=1对称,又f(x)是奇函数,当0≤x≤1时,f(x)=x,所以f(x)是周期为4的函数,其部分图象如图所示,
g(x)在[2 016,2 020]上零点的个数等价于g(x)在[0,4]上零点的个数,而g(x)在[0,4]上有无数个零点,故C错误;
当x≥0时,易知g(x)的最大值为2,由偶函数图象的对称性可知,当x<0时,g(x)的最大值也为2,所以g(x)在整个定义域上的最大值为2,故D正确.
综上可知,选AD.
(1,3]∪(4,+∞)
解析 令f(x)=0,当x≥λ时,x=4.当x<λ时,x2-4x+3=0,则x=1或x=3.若函数f(x)恰有2个零点,结合图1与图2知,1<λ≤3或λ>4.
9:30
解析 由题图可得函数图象过点(10,1),
设从喷洒药物开始经过t min顾客方可进入商场,易知t>10,
所以如果商场规定10:00顾客可以进入商场,那么开始喷洒药物的时间最迟是9:30.
9.已知a,b,c为正实数,且ln a=a-1,bln b=1,cec=1,则a,b,c的大小关系是______________.
c<a<b
由图象可知0<c<1,a=1,b>1,∴c<a<b.
(1)作出函数f(x)的图象;
解 函数f(x)的图象如图所示.
(3)若方程f(x)=m有两个不相等的正根,求实数m的取值范围.
解 由函数f(x)的图象可知,当0故实数m的取值范围为(0,1).
11.(2021·兰州质检)随着中国经济的快速发展,节能减耗刻不容缓.某市环保部门为了提高对所辖水域生态环境的巡查效率,引进了一种新型生态环保探测器,该探测器消耗能量由公式En=MvnT给出,其中M是质量(常数),v是设定速度(单位:km/h),T是行进时间(单位:h),n为参数.某次巡查为逆水行进,水流速度为4 km/h,行进路程为100 km.(逆水行进中,实际速度=设定速度-水流速度,顺水行进中,实际速度=设定速度+水流速度)
(1)求T关于v的函数关系式,并指出v的取值范围;
(2)①当参数n=2时,求探测器最低消耗能量;
②当参数n=3时,试确定使该探测器消耗的能量最低的设定速度.
因此,当参数n=2时,该探测器最低消耗能量为1 600M.
当4当v>6时,f′(v)>0,f(v)单调递增.
故当设定速度为6 km/h时,该探测器消耗的能量最低.
能力突破
12.基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln 2≈0.69)( )
A.1.2天 B.1.8天 C.2.5天 D.3.5天
B
解析 由R0=1+rT,R0=3.28,T=6,
由题意,累计感染病例数增加1倍,则I(t2)=2I(t1),
即e0.38t2=2e0.38t1,所以e0.38(t2-t1)=2,即0.38(t2-t1)=ln 2,
13.(多选)(2021·辽宁五校期末)方程ex+x-2=0的根为x1,ln x+x-2=0的根为x2,则( )
BD
解析 令f(x)=ex+x-2,g(x)=ln x+x-2,作出函数y=-x+2,y=ex,y=ln x的图象,其中y=ex与y=ln x互为反函数,其图象关于直线y=x对称,如图,则A(x1,ex1),B(x2,ln x2).
设直线y=x与y=-x+2的交点为C,则C(1,1),且A,B关于点C对称,∴ex1=x2,x1+x2=2.
∵ex1=x2,∴x1x2=x1ex1.
14.记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.
(1)证明:函数f(x)=x与g(x)=x2+2x-2不存在“S点”;
证明 函数f(x)=x,g(x)=x2+2x-2,
则f′(x)=1,g′(x)=2x+2.
由f(x)=g(x)且f′(x)=g′(x),得
因此,f(x)与g(x)不存在“S点”.
(2)若函数f(x)=ax2-1与g(x)=ln x存在“S点”,求实数a的值.
解 函数f(x)=ax2-1,g(x)=ln x,
设x0为f(x)与g(x)的“S点”,
由f(x0)=g(x0)且f′(x0)=g′(x0),得
即x0为f(x)与g(x)的“S点”.
上篇 专题六 函数与导数
第2讲 基本初等函数、函数的应用
高考定位
1.掌握二次函数、分段函数、幂函数、指数函数、对数函数的图象与性质;2.以基本初等函数为依托,考查函数与方程的关系、函数零点存在性定理;3.能利用函数解决简单的实际问题.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
1.(2020·全国Ⅲ卷)已知55<84,134<85.设a=log53,b=log85,c=log138,则( )
A.a
∴log53
∴log85
A.ln(y-x+1)>0 B.ln(y-x+1)<0
C.ln|x-y|>0 D.ln|x-y|<0
解析 设函数f(x)=2x-3-x.
因为函数y=2x与y=-3-x在R上均单调递增,
所以f(x)在R上单调递增.
原已知条件等价于2x-3-x<2y-3-y,
即f(x)
因为|x-y|与1的大小不能确定,所以C,D不正确.
A
解析 因为x2-2(a+1)x+a2+5=0最多有2个根,
所以cos (2πx-2πa)=0至少有4个根.
A
②当x≥a时,f(x)=x2-2(a+1)x+a2+5,
Δ=4(a+1)2-4(a2+5)=8(a-2),
当a<2时,Δ<0,f(x)无零点;
当a=2时,Δ=0,f(x)有1个零点x=3;
当a>2时,令f(a)=a2-2a(a+1)+a2+5=-2a+5≥0,则2<a≤,此时f(x)有2个零点;
4.(2021·北京卷)已知f(x)=|lg x|-kx-2,给出下列四个结论:
(1)若k=0,则f(x)有两个零点;
(2) k<0,使得f(x)有一个零点;
(3) k<0,使得f(x)有三个零点;
(4) k>0,使得f(x)有三个零点.
以上正确结论的序号是________.
(1)(2)(4)
解析 令f(x)=|lg x|-kx-2=0,
可转化成两个函数y1=|lg x|,y2=kx+2的图象的交点个数问题.
对于(1),当k=0时,y2=2与y1=|lg x|的图象有两个交点,(1)正确;
对于(2),存在k<0,使y2=kx+2与y1=|lg x|的图象相切,(2)正确;
对于(3),若k<0,则y1=|lg x|与y2=kx+2的图象最多有2个交点,(3)错误;
对于(4),当k>0时,过点(0,2)存在函数g(x)=lg x(x>1)图象的切线,此时共有两个交点,当直线斜率稍微小于相切时的斜率时,就会有3个交点,故(4)正确.
1.指数式与对数式的七个运算公式
2.指数函数与对数函数的图象和性质
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图象和性质,分0
(1)函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.
(2)确定函数零点的常用方法:①直接解方程法;②利用零点存在性定理;③数形结合,利用两个函数图象的交点求解.
4.应用函数模型解决实际问题的一般程序
2
热点聚焦 分类突破
热点一 基本初等函数的图象与性质
【例1】 (1)(多选)(2021·八省八校一联)下列命题中正确的是( )
ABC
D
解析 y=logax的图象关于y轴对称的图象对应的函数为y=loga(-x),函数f(x)的图象上有且仅有两个点关于y轴对称,等价于y=loga(-x)与y=|x+2|,-3≤x≤0的图象有且仅有一个交点.
当0<a<1时,显然符合题意(图略).
当a>1时,只需loga3>1,∴1<a<3.
综上所述,a的取值范围是(0,1)∪(1,3).
1.指数函数、对数函数的图象和性质受底数a的影响,解决与指数、对数函数特别是与单调性有关的问题时,首先要看底数a的范围.
2.基本初等函数的图象和性质是统一的,在解题中可相互转化.
探究提高
解析 易知f(x)在定义域R上为非奇非偶函数,B不合题意.
当x<0且x→-∞时,f(x)>0,且f(x)→+∞,C不合题意.
当x>0且x→+∞时,f(x)→0,知D不合题意,只有A满足.
A
(2)(多选)(2021·南京、盐城一模)已知函数f(x)=log2(1+4x)-x,则下列说法正确的是( )
A.函数f(x)是偶函数 B.函数f(x)是奇函数
C.函数f(x)在(-∞,0]上单调递增 D.函数f(x)的值域为[1,+∞)
AD
所以函数f(x)为偶函数,故A正确,B不正确;
则当x<0时,f′(x)<0,函数f(x)单调递减,当x>0时,f′(x)>0,函数f(x)单调递增,故C不正确;
由以上分析知,f(x)min=f(0)=1,
所以函数f(x)的值域为[1,+∞),故D正确.综上所述,选AD.
热点二 函数的零点与方程
考向1 确定函数零点个数
【例2】 (1)(2021·大连调研)设函数f(x)=2|x|+x2-3,则函数y=f(x)的零点个数是( )
A.4 B.3 C.2 D.1
C
解析 易知f(x)是偶函数,当x≥0时,f(x)=2x+x2-3,所以x≥0时,f(x)在[0,+∞)上是增函数,且f(1)=0,所以x=1是函数y=f(x)在[0,+∞)上的唯一零点.
根据奇偶性,知x=-1是y=f(x)在(-∞,0)内的零点,
因此y=f(x)有两个零点.
解析 当x≥0时,f(x)=4x3-6x2+1的导数为f′(x)=12x2-12x,
当0<x<1时,f(x)单调递减,x>1时,f(x)单调递增,
A
可得f(x)在x=1处取得最小值,最小值为-1,且f(0)=1,
作出函数f(x)的图象,如图.
g(x)=3[f(x)]2-10f(x)+3,
可令g(x)=0,t=f(x),可得3t2-10t+3=0,
即g(x)有三个零点;
当t=3时,可得f(x)=3有一个实根,即g(x)有一个零点.
综上,g(x)共有四个零点.
判断函数零点个数的主要方法
(1)解方程f(x)=0,直接求零点;(2)利用零点存在性定理;
(3)数形结合法:对于给定的函数不能直接求解或画出图象,常会通过分解转化为两个能画出图象的函数,求其图象交点问题.
探究提高
【训练2】 (1)函数f(x)=2sin x-sin 2x在[0,2π]的零点个数为( )
A.2 B.3 C.4 D.5
B
解析 令f(x)=0,得2sin x-sin 2x=0,
即2sin x-2sin xcos x=0,
∴2sin x(1-cos x)=0,∴sin x=0或cos x=1.
又x∈[0,2π],
∴由sin x=0得x=0,π或2π,由cos x=1得x=0或2π.
故函数f(x)的零点为0,π,2π,共3个.
解析 对于任意的x∈R,都有f(2+x)=f(2-x),
∴f(x+4)=f[2+(x+2)]=f[2-(x+2)]=f(-x)=f(x),
∴函数f(x)是一个周期函数,且T=4.
C
则函数y=f(x)与y=log8(x+2)在区间(-2,6)上的图象如图所示,
根据图象可得y=f(x)与y=log8(x+2)在区间(-2,6)上有3个不同的交点,即f(x)-log8(x+2)=0在区间(-2,6)上有3个根.
考向2 根据函数的零点求参数的值或范围
【例3】 (1)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=( )
C
解析 f(x)=(x-1)2+a(ex-1+e1-x)-1,
令t=x-1,则g(t)=f(t+1)=t2+a(et+e-t)-1.
∵g(-t)=(-t)2+a(e-t+et)-1=g(t),且t∈R,
∴函数g(t)为偶函数.
∵f(x)有唯一零点,∴g(t)也有唯一零点.
又g(t)为偶函数,由偶函数的性质知g(0)=0,
解析 由题意,令y=f(x)-ax-b=0,得
C
则以上两个函数的图象恰有3个交点,根据选项进行讨论.
①当a<-1时,1-a>0,可知在x∈(-∞,0)上,g(x)单调递增,且g(x)<0;
由g′(x)=x2-(a+1)x=x[x-(a+1)](x≥0),a+1<0,
可知在x∈[0,+∞)上,g(x)单调递增,且g(x)≥0.
此时直线y=b与g(x)的图象只有1个交点,不符合题意,故排除A,B.
②当a>-1,即a+1>0时.
因为g′(x)=x[x-(a+1)](x≥0),所以当x≥0时,
由g′(x)<0可得0
所以当x≥0时,g(x)在(0,a+1)上单调递减,g(x)在(a+1,+∞)上单调递增.
如图,y=b与y=g(x)(x≥0)的图象至多有2个交点.
当1-a>0,即-1
当1-a<0,即a>1时,y=g(x)与y=b的图象可以有1个或2个交点,但不存在恰有3个交点的情况,不符合题意,舍去.
综上,-1
2.解决由函数零点的存在情况求参数的值或取值范围问题,关键是利用函数方程思想或数形结合思想,构建关于参数的方程或不等式求解.
探究提高
【训练3】 设函数f(x)=ex(2x-1)-ax+a(a<1)有两个零点,则实数a的取值范围是( )
A
解析 依题设,f(x)=ex(2x-1)-ax+a有两个零点,
∴函数y=ex(2x-1)的图象与直线y=a(x-1)有两个交点.
设直线y=a(x-1)与y=ex(2x-1)相切于点P(x0,y0),
∴y0=ex0(2x0-1).
则过点P(x0,y0)的切线为
y-ex0(2x0-1)=ex0(2x0+1)(x-x0).
此时,直线y=a(x-1)的斜率为1.
故若直线y=a(x-1)与函数y=ex(2x-1)的图象有两个交点,应有0
(1)求桥AB的长度;
解 如图,设AA1,BB1,CD1,EF1都与MN垂直,A1,B1,D1,F1是相应垂足.
由条件知,当O′B=40时,
得O′A=80.
所以AB=O′A+O′B=80+40=120(米).
解 以O为原点,OO′所在直线为y轴建立平面直角坐标系xOy(如图所示).
因为CE=80,所以O′C=80-x.
记桥墩CD和EF的总造价为f(x)万元,
令f′(x)=0,得x=20或x=0(舍去).
列表如下:
X (0,20) 20 (20,40)
f′(x) - 0 +
f(x) ? 极小值 ?
所以当x=20时,f(x)取得最小值.
答:(1)桥AB的长度为120米;
(2)当O′E为20米时,桥墩CD与EF的总造价最低.
1.解决函数的实际应用问题时,首先要耐心、细心地审清题意,弄清各量之间的关系,再建立函数关系式,然后借助函数的知识求解,解答后再回到实际问题中去.
2.对函数模型求最值的常用方法:单调性法、基本不等式法及导数法.
探究提高
【训练4】 (2021·西南名校联考)“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=eax+b(a,b为常数),若该果蔬在6 ℃的保鲜时间为216小时,在24 ℃的保鲜时间为8小时,且该果蔬所需物流时间为3天,则物流过程中果蔬的储藏温度(假设物流过程中恒温)最高不能超过( )
A.9 ℃ B.12 ℃ C.18 ℃ D.20 ℃
B
解析 当x=6时,e6a+b=216;当x=24时,e24a+b=8,
故物流过程中果蔬的储藏温度最高不能超过12 ℃.
专题训练 对接高考
3
巩固提升
A.a<b<c B.c<a<b C.b<c<a D.a<c<b
D
解析 ∵log20.3<log21=0,∴a<0.
∵0<0.40.3<0.40=1,∴0<c<1,
∴a<c<b.
A.2 B.3 C.4 D.5
解析 由f(x+1)=-f(x),得f(x+2)=f(x),知周期T=2.
令f(x)-|x|=0,得f(x)=|x|.
作出函数y=f(x)与g(x)=|x|的图象如图所示.
A
由图象知,函数y=f(x)-|x|有两个零点.
A.60 B.63 C.66 D.69
C
B
所以g(x)在(0,1)上必然存在零点,
即x0∈(0,1),
因此f(x0)=[x0]=0,
所以g[f(x0)]=g(0)=-2.
5.(多选)(2021·江苏调考)若0
A.logac>logbc B.abc>bac
C.alogbc>blogac D.a(b-c)>b(a-c)
AB
所以0>logac>logbc,故A正确;
对于B,因为0
所以bc-1>ac-1,又ab>0,所以由不等式的基本性质得abc>bac,故B正确;
对于C,由A知logbc
A.g(x)为偶函数 B.g(x)在(1,2)上单调递增
C.g(x)在[2 016,2 020]上恰有三个零点 D.g(x)的最大值为2
AD
解析 易知函数g(x)的定义域为R,
且g(-x)=|f(-x)|+f(|-x|)=|-f(x)|+f(|x|)=|f(x)|+f(|x|)=g(x),
所以g(x)为偶函数,故A正确;
因为f(1+x)=f(1-x),所以f(x)的图象关于直线x=1对称,又f(x)是奇函数,当0≤x≤1时,f(x)=x,所以f(x)是周期为4的函数,其部分图象如图所示,
g(x)在[2 016,2 020]上零点的个数等价于g(x)在[0,4]上零点的个数,而g(x)在[0,4]上有无数个零点,故C错误;
当x≥0时,易知g(x)的最大值为2,由偶函数图象的对称性可知,当x<0时,g(x)的最大值也为2,所以g(x)在整个定义域上的最大值为2,故D正确.
综上可知,选AD.
(1,3]∪(4,+∞)
解析 令f(x)=0,当x≥λ时,x=4.当x<λ时,x2-4x+3=0,则x=1或x=3.若函数f(x)恰有2个零点,结合图1与图2知,1<λ≤3或λ>4.
9:30
解析 由题图可得函数图象过点(10,1),
设从喷洒药物开始经过t min顾客方可进入商场,易知t>10,
所以如果商场规定10:00顾客可以进入商场,那么开始喷洒药物的时间最迟是9:30.
9.已知a,b,c为正实数,且ln a=a-1,bln b=1,cec=1,则a,b,c的大小关系是______________.
c<a<b
由图象可知0<c<1,a=1,b>1,∴c<a<b.
(1)作出函数f(x)的图象;
解 函数f(x)的图象如图所示.
(3)若方程f(x)=m有两个不相等的正根,求实数m的取值范围.
解 由函数f(x)的图象可知,当0
11.(2021·兰州质检)随着中国经济的快速发展,节能减耗刻不容缓.某市环保部门为了提高对所辖水域生态环境的巡查效率,引进了一种新型生态环保探测器,该探测器消耗能量由公式En=MvnT给出,其中M是质量(常数),v是设定速度(单位:km/h),T是行进时间(单位:h),n为参数.某次巡查为逆水行进,水流速度为4 km/h,行进路程为100 km.(逆水行进中,实际速度=设定速度-水流速度,顺水行进中,实际速度=设定速度+水流速度)
(1)求T关于v的函数关系式,并指出v的取值范围;
(2)①当参数n=2时,求探测器最低消耗能量;
②当参数n=3时,试确定使该探测器消耗的能量最低的设定速度.
因此,当参数n=2时,该探测器最低消耗能量为1 600M.
当4
故当设定速度为6 km/h时,该探测器消耗的能量最低.
能力突破
12.基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln 2≈0.69)( )
A.1.2天 B.1.8天 C.2.5天 D.3.5天
B
解析 由R0=1+rT,R0=3.28,T=6,
由题意,累计感染病例数增加1倍,则I(t2)=2I(t1),
即e0.38t2=2e0.38t1,所以e0.38(t2-t1)=2,即0.38(t2-t1)=ln 2,
13.(多选)(2021·辽宁五校期末)方程ex+x-2=0的根为x1,ln x+x-2=0的根为x2,则( )
BD
解析 令f(x)=ex+x-2,g(x)=ln x+x-2,作出函数y=-x+2,y=ex,y=ln x的图象,其中y=ex与y=ln x互为反函数,其图象关于直线y=x对称,如图,则A(x1,ex1),B(x2,ln x2).
设直线y=x与y=-x+2的交点为C,则C(1,1),且A,B关于点C对称,∴ex1=x2,x1+x2=2.
∵ex1=x2,∴x1x2=x1ex1.
14.记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.
(1)证明:函数f(x)=x与g(x)=x2+2x-2不存在“S点”;
证明 函数f(x)=x,g(x)=x2+2x-2,
则f′(x)=1,g′(x)=2x+2.
由f(x)=g(x)且f′(x)=g′(x),得
因此,f(x)与g(x)不存在“S点”.
(2)若函数f(x)=ax2-1与g(x)=ln x存在“S点”,求实数a的值.
解 函数f(x)=ax2-1,g(x)=ln x,
设x0为f(x)与g(x)的“S点”,
由f(x0)=g(x0)且f′(x0)=g′(x0),得
即x0为f(x)与g(x)的“S点”.
同课章节目录
