规范答题示范课——函数与导数解答题 课件(共15张PPT)
文档属性
| 名称 | 规范答题示范课——函数与导数解答题 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 542.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 22:35:19 | ||
图片预览






文档简介
(共15张PPT)
上篇 专题六 函数与导数
规范答题示范课——函数与导数解答题
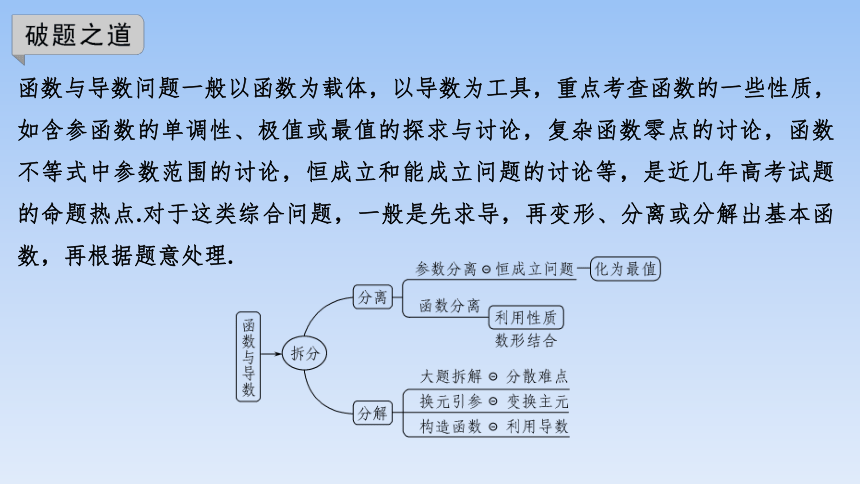
函数与导数问题一般以函数为载体,以导数为工具,重点考查函数的一些性质,如含参函数的单调性、极值或最值的探求与讨论,复杂函数零点的讨论,函数不等式中参数范围的讨论,恒成立和能成立问题的讨论等,是近几年高考试题的命题热点.对于这类综合问题,一般是先求导,再变形、分离或分解出基本函数,再根据题意处理.
(2)若曲线y=f(x)与直线y=1有且仅有两个交点,求a的取值范围.
解 曲线y=f(x)与直线y=1有且仅有两个交点,
当0<x<e时,g′(x)>0,函数g(x)单调递增,
当x>e时,g′(x)<0,函数g(x)单调递减,
故a的取值范围为(1,e)∪(e,+∞). 12分
得计算分:解题过程中计算准确是得满分的根本保证.如第(1)问中,求导f′(x)准确,否则全盘皆输;第(2)问中正确求g′(x)及g(x)max,数形结合得不等式组,并准确计算出a>1,且a≠e,否则导致失分.
1.已知函数f(x)=ln x,g(x)=x+m(m∈R).
(1)若f(x)≤g(x)恒成立,求实数m的取值范围;
解 令F(x)=f(x)-g(x)=ln x-x-m(x>0),
当x>1时,F′(x)<0,当00,
所以F(x)在(1,+∞)上单调递减,在(0,1)上单调递增.
所以F(x)在x=1处取得最大值-1-m.
若f(x)≤g(x)恒成立,则-1-m≤0,即m≥-1.
故m的取值范围为[-1,+∞).
(2)已知x1,x2是函数F(x)=f(x)-g(x)的两个零点,且x1证明 由(1)可知,若函数F(x)=f(x)-g(x)有两个零点,有F(1)>0,则m<-1,0由F(x1)=F(x2)=0,m=ln x1-x1,
故h(x)在(0,1)上单调递增,
h(x)所以x1x2<1.
2.(2021·天津卷)已知a>0,函数f(x)=ax-xex.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
解 f′(x)=a-(x+1)ex,则f′(0)=a-1,
又f(0)=0,则所求切线方程为y=(a-1)x(a>0).
(2)证明函数y=f(x)存在唯一的极值点;
证明 令f′(x)=a-(x+1)ex=0,则a=(x+1)ex.
令g(x)=(x+1)ex,则g′(x)=(x+2)ex.
当x∈(-∞,-2)时,g′(x)<0,g(x)单调递减;当x∈(-2,+∞)时,g′(x)>0,g(x)单调递增.
又当x→-∞时,g(x)<0,当x→+∞时,g(x)>0,
又g(-1)=0,故画出g(x)的大致图象如下:
所以当a>0时,y=a与y=g(x)的图象仅有一个交点.
令g(m)=a,则m>-1,且f′(m)=a-g(m)=0.
当x∈(-∞,m)时,a>g(x),则f′(x)>0,f(x)单调递增;当x∈(m,+∞)时,a<g(x),则f′(x)<0,f(x)单调递减,
所以x=m为f(x)的极大值点,
故f(x)存在唯一的极值点.
(3)若存在实数a,使得f(x)≤a+b对任意x∈R成立,求实数b的取值范围.
解 由(2)知f(x)max=f(m),此时a=(1+m)em,且m>-1,
所以(f(x)-a)max=f(m)-a
=(m2-m-1)em,m>-1.
令h(x)=(x2-x-1)ex(x>-1),
若存在a,使得f(x)≤a+b对任意x∈R成立,等价于存在x∈(-1,+∞),使得h(x)≤b,即b≥h(x)min.
h′(x)=(x2+x-2)ex=(x-1)(x+2)ex,x>-1,
当x∈(-1,1)时,h′(x)<0,h(x)单调递减;当x∈(1,+∞)时,h′(x)>0,h(x)在(1,+∞)上单调递增,
所以h(x)min=h(1)=-e,故b≥-e,
所以实数b的取值范围为[-e,+∞).
上篇 专题六 函数与导数
规范答题示范课——函数与导数解答题
函数与导数问题一般以函数为载体,以导数为工具,重点考查函数的一些性质,如含参函数的单调性、极值或最值的探求与讨论,复杂函数零点的讨论,函数不等式中参数范围的讨论,恒成立和能成立问题的讨论等,是近几年高考试题的命题热点.对于这类综合问题,一般是先求导,再变形、分离或分解出基本函数,再根据题意处理.
(2)若曲线y=f(x)与直线y=1有且仅有两个交点,求a的取值范围.
解 曲线y=f(x)与直线y=1有且仅有两个交点,
当0<x<e时,g′(x)>0,函数g(x)单调递增,
当x>e时,g′(x)<0,函数g(x)单调递减,
故a的取值范围为(1,e)∪(e,+∞). 12分
得计算分:解题过程中计算准确是得满分的根本保证.如第(1)问中,求导f′(x)准确,否则全盘皆输;第(2)问中正确求g′(x)及g(x)max,数形结合得不等式组,并准确计算出a>1,且a≠e,否则导致失分.
1.已知函数f(x)=ln x,g(x)=x+m(m∈R).
(1)若f(x)≤g(x)恒成立,求实数m的取值范围;
解 令F(x)=f(x)-g(x)=ln x-x-m(x>0),
当x>1时,F′(x)<0,当0
所以F(x)在(1,+∞)上单调递减,在(0,1)上单调递增.
所以F(x)在x=1处取得最大值-1-m.
若f(x)≤g(x)恒成立,则-1-m≤0,即m≥-1.
故m的取值范围为[-1,+∞).
(2)已知x1,x2是函数F(x)=f(x)-g(x)的两个零点,且x1
故h(x)在(0,1)上单调递增,
h(x)
2.(2021·天津卷)已知a>0,函数f(x)=ax-xex.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
解 f′(x)=a-(x+1)ex,则f′(0)=a-1,
又f(0)=0,则所求切线方程为y=(a-1)x(a>0).
(2)证明函数y=f(x)存在唯一的极值点;
证明 令f′(x)=a-(x+1)ex=0,则a=(x+1)ex.
令g(x)=(x+1)ex,则g′(x)=(x+2)ex.
当x∈(-∞,-2)时,g′(x)<0,g(x)单调递减;当x∈(-2,+∞)时,g′(x)>0,g(x)单调递增.
又当x→-∞时,g(x)<0,当x→+∞时,g(x)>0,
又g(-1)=0,故画出g(x)的大致图象如下:
所以当a>0时,y=a与y=g(x)的图象仅有一个交点.
令g(m)=a,则m>-1,且f′(m)=a-g(m)=0.
当x∈(-∞,m)时,a>g(x),则f′(x)>0,f(x)单调递增;当x∈(m,+∞)时,a<g(x),则f′(x)<0,f(x)单调递减,
所以x=m为f(x)的极大值点,
故f(x)存在唯一的极值点.
(3)若存在实数a,使得f(x)≤a+b对任意x∈R成立,求实数b的取值范围.
解 由(2)知f(x)max=f(m),此时a=(1+m)em,且m>-1,
所以(f(x)-a)max=f(m)-a
=(m2-m-1)em,m>-1.
令h(x)=(x2-x-1)ex(x>-1),
若存在a,使得f(x)≤a+b对任意x∈R成立,等价于存在x∈(-1,+∞),使得h(x)≤b,即b≥h(x)min.
h′(x)=(x2+x-2)ex=(x-1)(x+2)ex,x>-1,
当x∈(-1,1)时,h′(x)<0,h(x)单调递减;当x∈(1,+∞)时,h′(x)>0,h(x)在(1,+∞)上单调递增,
所以h(x)min=h(1)=-e,故b≥-e,
所以实数b的取值范围为[-e,+∞).
同课章节目录
