第1讲 函数的图象与性质 课件(共60张PPT)
文档属性
| 名称 | 第1讲 函数的图象与性质 课件(共60张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 22:37:21 | ||
图片预览











文档简介
(共60张PPT)
上篇 专题六 函数与导数
第1讲 函数的图象与性质
高考定位
1.以基本初等函数为载体,考查函数的定义域、值域、最值、奇偶性、单调性和周期性;2.利用函数的图象研究函数性质,能用函数的图象与性质解决简单问题;3.函数与方程思想、数形结合思想是高考的重要思想方法.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
A.f(x-1)-1 B.f(x-1)+1
C.f(x+1)-1 D.f(x+1)+1
B
对于选项C,D,显然定义域不关于原点对称,故为非奇非偶函数.
D
因为当x∈(0,+∞)时,f(x)单调递增,且f(x)>0,
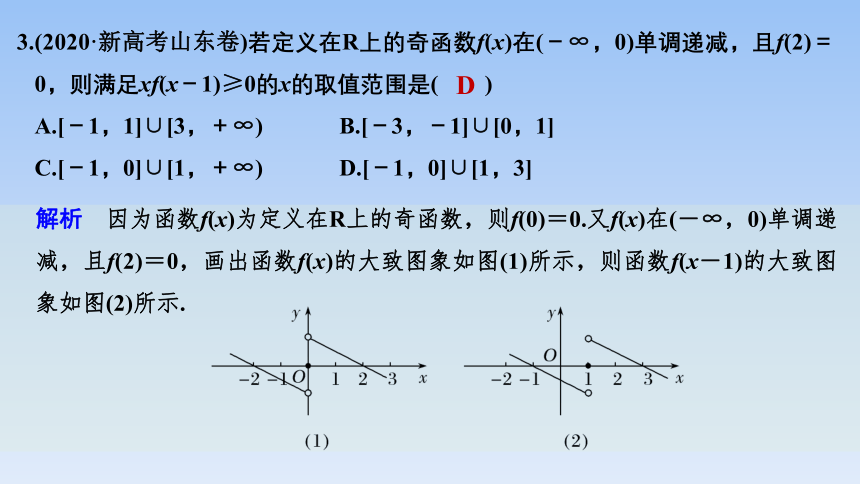
3.(2020·新高考山东卷)若定义在R上的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是( )
A.[-1,1]∪[3,+∞) B.[-3,-1]∪[0,1]
C.[-1,0]∪[1,+∞) D.[-1,0]∪[1,3]
D
解析 因为函数f(x)为定义在R上的奇函数,则f(0)=0.又f(x)在(-∞,0)单调递减,且f(2)=0,画出函数f(x)的大致图象如图(1)所示,则函数f(x-1)的大致图象如图(2)所示.
当x≤0时,要满足xf(x-1)≥0,则f(x-1)≤0,
得-1≤x≤0.
当x>0时,要满足xf(x-1)≥0,则f(x-1)≥0,
得1≤x≤3.
故满足xf(x-1)≥0的x的取值范围是[-1,0]∪[1,3].
故选D.
4.(2021·新高考Ⅰ卷)函数f(x)=|2x-1|-2ln x的最小值为________.
1
解析 函数f(x)=|2x-1|-2ln x的定义域为(0,+∞).
综上,f(x)min=1.
1.函数的图象
(1)对于函数的图象要会作图、识图和用图,作函数图象有两种基本方法:一是描点法;二是图象变换法,其中图象变换有平移变换、伸缩变换和对称变换.
(2)在研究函数性质特别是单调性、值域、零点时,要注意结合其图象研究.
(3)函数图象的对称性
①若函数y=f(x)满足f(a+x)=f(a-x),即f(x)=f(2a-x),则y=f(x)的图象关于直线x=a对称;
②若函数y=f(x)满足f(a+x)=-f(a-x),即f(x)=-f(2a-x),则y=f(x)的图象关于点(a,0)对称.
2.函数的性质
(1)单调性:单调性是函数在其定义域上的局部性质.证明函数的单调性时,规范步骤为取值、作差、变形、判断符号和下结论.复合函数的单调性遵循“同增异减”的原则.
(2)奇偶性:①若f(x)是偶函数,则f(x)=f(-x).
②若f(x)是奇函数,0在其定义域内,则f(0)=0.
③奇函数在关于原点对称的单调区间内有相同的单调性,偶函数在关于原点对称的单调区间内有相反的单调性.
2
热点聚焦 分类突破
热点一 函数及其表示
A.(1,2] B.(2,4] C.[1,2) D.[2,4)
B
D
综上,不等式f(x)≤5的解集为[-2,3].
1.(1)给出解析式的函数的定义域是使解析式有意义的自变量的集合,只需构建不等式(组)求解即可.
(2)抽象函数:根据f(g(x))中g(x)的范围与f(x)中x的范围相同求解.
2.对于分段函数求值或解不等式问题,一定要根据变量的取值条件进行分段讨论.
探究提高
A
解析 当x≥1时,f(x)=2x-1≥1,
热点二 函数的图象及应用
B
当x∈(0,1)时,ln|x|<0,x2+2>0,所以f(x)<0,排除D.故选B.
(2)已知函数f(x)=2x-x-1,则不等式f(x)>0的解集是( )
A.(-1,1) B.(-∞,-1)∪(1,+∞)
C.(0,1) D.(-∞,0)∪(1,+∞)
D
解析 在同一平面直角坐标系中画出h(x)=2x,g(x)=x+1的图象如图.由图象得交点坐标为(0,1)和(1,2).
又f(x)>0等价于2x>x+1,
结合图象,可得x<0或x>1.
故f(x)>0的解集为(-∞,0)∪(1,+∞).
1.函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不符合要求的图象.
2.(1)运用函数图象解决问题时,先要正确理解和把握函数图象本身的含义及其表示的内容,熟悉图象所能够表达的函数的性质.(2)图象形象地显示了函数的性质,因此,函数性质的确定与应用及一些方程、不等式的求解常与图象数形结合研究.
探究提高
A
所以f(x)是偶函数,图象关于y轴对称,排除C,D.
当0(2)已知函数f(x)在R上单调且其部分图象如图所示,若不等式-21
解析 由图象可知不等式-2即f(3)又y=f(x)在R上单调递减,
所以0依题意,得t=1.
热点三 函数的性质及应用
D
解析 由于f(x+1)为奇函数,所以函数f(x)的图象关于点(1,0)对称,
即有f(x)+f(2-x)=0,
所以f(1)+f(2-1)=0,得f(1)=0,即a+b=0 ①.
由于f(x+2)为偶函数,所以函数f(x)的图象关于直线x=2对称,
即有f(x)-f(4-x)=0,
所以f(0)+f(3)=-f(2)+f(1)=-4a-b+a+b=-3a=6 ②.
根据①②可得a=-2,b=2,
所以当x∈[1,2]时,f(x)=-2x2+2.
根据函数f(x)的图象关于直线x=2对称,且关于点(1,0)对称,可得函数f(x)的周期为4,
(2)(多选)已知函数f(x)的定义域为R,且f(x+1)是偶函数,f(x-1)是奇函数,则下列说法正确的是( )
A.f(7)=0 B.f(x)的一个周期为8
C.f(x)图象的一个对称中心为(3,0) D.f(x)图象的一条对称轴为直线x=2 019
ABC
解析 依题意知,直线x=1是f(x)图象的一条对称轴,(-1,0)是f(x)图象的一个对称中心,又因为f(x+1)是偶函数,f(x-1)是奇函数,所以f(x+1)=f(-x+1),f(x-1)=-f(-x-1),所以f(x)=f(-x+2),f(x)=-f(-x-2),所以f(-x+2)=-f(-x-2),所以f(x+2)=-f(x-2),所以f(x)=-f(x-4)=-[-f(x-8)]=f(x-8),所以f(x)是周期函数,且8为函数f(x)的一个周期,故B正确;
f(7)=f(-1)=0,故A正确;
因为f(x)图象上每隔4个单位长度出现一个对称中心,所以点(3,0)是函数f(x)图象的一个对称中心,故C正确;
x=2 019=8×252+3,所以直线x=2 019不是函数f(x)图象的对称轴,故D错误,故选ABC.
考向2 函数的单调性与奇偶性
AD
A.f(x)为奇函数 B.f(x)为偶函数
C.f(x)在R上单调递增 D.f(x)在R上单调递减
解析 由题意知函数f(x)的定义域为R,关于原点对称.对任意x∈R,
C
1.利用函数的奇偶性和周期性可以转化函数的解析式、图象和性质,把不在已知区间上的问题,转化到已知区间上求解.
2.函数单调性的应用:可以比较大小、求函数最值、解不等式、证明方程根的唯一性.
探究提高
【训练3】 (1)(2021·新高考Ⅱ卷)已知函数f(x)的定义域为R,f(x+2)为偶函数,f(2x+1)为奇函数,则( )
B
解析 因为函数f(x+2)为偶函数,则f(2+x)=f(2-x),可得f(x+3)=f(1-x).
因为函数f(2x+1)为奇函数,则f(1-2x)=-f(2x+1),
所以f(1-x)=-f(x+1),
所以f(x+3)=-f(x+1)=f(x-1),
即f(x)=f(x+4),
故函数f(x)是以4为周期的周期函数.
因为函数F(x)=f(2x+1)为奇函数,则F(0)=f(1)=0,故f(-1)=-f(1)=0,其它三个选项未知,不能确定数值.
(2)(2021·衡水模拟)已知定义在R上的可导函数f(x),对任意的实数x,都有f(x)-f(-x)=2x,且当x∈(0,+∞)时,f′(x)>1恒成立,若不等式f(a)-f(1-a)≥2a-1恒成立,则实数a的取值范围是( )
A
解析 由f(x)-f(-x)=2x,
得f(x)-x=f(-x)-(-x).
设F(x)=f(x)-x,则F(-x)=F(x),F(x)为偶函数.
由f′(x)>1,知F′(x)=f′(x)-1>0,
∴函数F(x)在(0,+∞)上单调递增.
由f(a)-f(1-a)≥2a-1,得f(a)-a≥f(1-a)-(1-a),
∴F(a)≥F(1-a) F(|a|)≥F(|1-a|),
专题训练 对接高考
3
巩固提升
一、选择题
1.(2021·北京卷)设函数f(x)的定义域为[0,1],则“函数f(x)在[0,1]上单调递增”是“函数f(x)在[0,1]上的最大值为f(1)”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
A
解析 显然f(-x)=-f(x),x∈[-π,π],所以f(x)为奇函数,排除A;
D
3.(2021·广州模拟)已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+a,则g(2)=( )
A.-4 B.4 C.-8 D.8
解析 依题意f(x)是偶函数,g(x)是奇函数,
且f(x)-g(x)=x3+x2+a,①
所以f(-x)-g(-x)=-x3+x2+a,
即f(x)+g(x)=-x3+x2+a,②
②-①得2g(x)=-2x3,g(x)=-x3,所以g(2)=-23=-8.故选C.
C
4.设f(x)是定义域为R的偶函数,且在(0,+∞)上单调递减,则( )
C
解析 因为f(x)是定义域为R的偶函数,
5.(多选)(2021·辽宁五校期末)定义在实数集R上的函数f(x)满足f(1+x)=-f(1-x),且x≥1时,函数f(x)单调递增,则( )
A.f(1)=0 B.f(x)是周期函数
C.方程f(x)=0有唯一实数解 D.函数f(x)在(-∞,0)上单调递减
AC
解析 ∵x∈R,f(1+x)=-f(1-x),
∴函数f(x)的图象关于点(1,0)成中心对称.
令x=0,则f(1)=-f(1),即f(1)=0.
又∵当x≥1时,函数f(x)单调递增,∴当x<1时,函数f(x)单调递增,∴f(x)不是周期函数,∴方程f(x)=0有唯一实数解.
∴A,C正确,B,D错误.故选AC.
6.设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)( )
D
又f(-x)=ln|-2x+1|-ln|-2x-1|=ln|2x-1|-ln|2x+1|=-f(x),
∴f(x)为奇函数,故排除A,C;
二、填空题
7.(2021·新高考Ⅰ卷)已知函数f(x)=x3(a·2x-2-x)是偶函数,则a=________.
1
解析 法一 因为f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数,
所以f(-x)=f(x)对任意的x∈R恒成立,
所以(-x)3(a·2-x-2x)=x3(a·2x-2-x)对任意的x∈R恒成立,
所以x3(a-1)(2x+2-x)=0对任意的x∈R恒成立,所以a=1.
法二 因为f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数,
经检验,f(x)=x3(2x-2-x)为偶函数,所以a=1.
法三 由题意知f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数.
设g(x)=x3,h(x)=a·2x-2-x,因为g(x)=x3为奇函数,
所以h(x)=a·2x-2-x为奇函数,
所以h(0)=a·20-2-0=0,解得a=1,
经检验,f(x)=x3(2x-2-x)为偶函数,所以a=1.
-ln 4
解析 ∵f(-1)=f(1),∴2-1=log2(1-a),
易知x<0时,f(x)=2x∈(0,1);
又x≥0时,f(x)=log2(x-a)递增,
故f(x)≥f(0)=log2(-a).
解得-1≤a<0.
10.设函数f(x)=ex+ae-x(a为常数).若f(x)为奇函数,则a=________;若f(x)是R上的增函数,则a的取值范围是________.
-1
(-∞,0]
解析 奇函数f(x)=ex+ae-x(a为常数)的定义域为R,
∴f(0)=e0+ae-0=1+a=0,∴a=-1(经验证符合题意).
∵f(x)是R上的增函数,∴f′(x)≥0在R上恒成立,
又e2x>0,∴a≤0,即a的取值范围是(-∞,0].
(1)求f(0);
(2)探究f(x)的单调性,并证明你的结论;
解 f(x)在R上单调递增,证明如下:
∵f(x)的定义域为R,∴任取x1,x2∈R且x1∵y=2x在R上单调递增且x1∴0<2x1<2x2,∴2x1-2x2<0,2x1+1>0,2x2+1>0,
∴f(x1)-f(x2)<0,即f(x1)∴f(x)在R上单调递增.
(3)若f(x)为奇函数,解不等式f(ax)解 ∵f(x)是奇函数,∴f(-x)=-f(x),
∴f(ax)又∵f(x)在R上单调递增,∴x<2.
∴不等式的解集为(-∞,2).
能力突破
12.(多选)(2021·济南统考)设函数f(x)=min{|x-2|,x2,|x+2|},其中min{x,y,z}表示x,y,z中的最小者,则下列说法正确的是( )
A.函数f(x)为偶函数 B.当x∈[1,+∞)时,f(x-2)≤f(x)
C.当x∈R时,f(f(x))≤f(x) D.当x∈[-4,4]时,|f(x)-2|≥f(x)
ABC
解析 在同一平面直角坐标系中分别画出函数y=|x-2|,y=x2,y=|x+2|的图象如图所示,
显然f(-x)=f(x),故f(x)为偶函数,故A正确;
当x≥1时,f(x)=|x-2|,f(x-2)的图象可由f(x)的图象向右平移2个单位长度得到,显然当x≥1时,f(x)的图象不在f(x-2)图象的下方,即当x∈[1,+∞)时,f(x-2)≤f(x),故B正确;
由图可知,当x∈R时,f(x)≥0,令t=f(x),t≥0,由y=f(t)和y=t(t≥0)的图象可知,当t≥0时,直线y=t不在曲线y=f(t)的下方,所以当t≥0时,t≥f(t),即f(f(x))≤f(x),故C正确;
当x∈[-4,4]时,f(-4)=2,f(-4)-2=0,显然f(-4)>|f(-4)-2|,故D不正确.故选ABC.
解析 因为函数f(x)为奇函数,所以f(x)=-f(-x),
所以f(2-x)+f(x)=-f(x-2)+f(x)=0,
即f(x-2)=f(x),
所以f(x)是以2为周期的周期函数.
14.已知函数f(x+1)是定义在R上的偶函数, x1,x2∈[1,+∞),且x1≠x2,都有(x1-x2)[f(x2)-f(x1)]<0,则不等式f(-2x+1+1)<f(5)的解集为________.
(-∞,1)
解析 因为函数f(x+1)是定义在R上的偶函数,
所以f(x+1)的图象关于y轴对称.
因为f(x)的图象向左平移1个单位长度得到f(x+1)的图象,
所以f(x)的图象关于直线x=1对称.
因为 x1,x2∈[1,+∞),且x1≠x2,
都有(x1-x2)[f(x2)-f(x1)]<0,
所以函数f(x)在[1,+∞)上单调递增,
由此可得函数f(x)在(-∞,1)上单调递减.
因为f(-2x+1+1)<f(5),
且f(5)=f(-3),-2x+1+1<1,
所以-2x+1+1>-3,即2x+1<4,解得x<1,
所以所求不等式的解集为(-∞,1).
上篇 专题六 函数与导数
第1讲 函数的图象与性质
高考定位
1.以基本初等函数为载体,考查函数的定义域、值域、最值、奇偶性、单调性和周期性;2.利用函数的图象研究函数性质,能用函数的图象与性质解决简单问题;3.函数与方程思想、数形结合思想是高考的重要思想方法.
真题感悟 考点整合
热点聚焦 分类突破
专题训练 对接高考
内容索引
真题感悟 考点整合
1
A.f(x-1)-1 B.f(x-1)+1
C.f(x+1)-1 D.f(x+1)+1
B
对于选项C,D,显然定义域不关于原点对称,故为非奇非偶函数.
D
因为当x∈(0,+∞)时,f(x)单调递增,且f(x)>0,
3.(2020·新高考山东卷)若定义在R上的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是( )
A.[-1,1]∪[3,+∞) B.[-3,-1]∪[0,1]
C.[-1,0]∪[1,+∞) D.[-1,0]∪[1,3]
D
解析 因为函数f(x)为定义在R上的奇函数,则f(0)=0.又f(x)在(-∞,0)单调递减,且f(2)=0,画出函数f(x)的大致图象如图(1)所示,则函数f(x-1)的大致图象如图(2)所示.
当x≤0时,要满足xf(x-1)≥0,则f(x-1)≤0,
得-1≤x≤0.
当x>0时,要满足xf(x-1)≥0,则f(x-1)≥0,
得1≤x≤3.
故满足xf(x-1)≥0的x的取值范围是[-1,0]∪[1,3].
故选D.
4.(2021·新高考Ⅰ卷)函数f(x)=|2x-1|-2ln x的最小值为________.
1
解析 函数f(x)=|2x-1|-2ln x的定义域为(0,+∞).
综上,f(x)min=1.
1.函数的图象
(1)对于函数的图象要会作图、识图和用图,作函数图象有两种基本方法:一是描点法;二是图象变换法,其中图象变换有平移变换、伸缩变换和对称变换.
(2)在研究函数性质特别是单调性、值域、零点时,要注意结合其图象研究.
(3)函数图象的对称性
①若函数y=f(x)满足f(a+x)=f(a-x),即f(x)=f(2a-x),则y=f(x)的图象关于直线x=a对称;
②若函数y=f(x)满足f(a+x)=-f(a-x),即f(x)=-f(2a-x),则y=f(x)的图象关于点(a,0)对称.
2.函数的性质
(1)单调性:单调性是函数在其定义域上的局部性质.证明函数的单调性时,规范步骤为取值、作差、变形、判断符号和下结论.复合函数的单调性遵循“同增异减”的原则.
(2)奇偶性:①若f(x)是偶函数,则f(x)=f(-x).
②若f(x)是奇函数,0在其定义域内,则f(0)=0.
③奇函数在关于原点对称的单调区间内有相同的单调性,偶函数在关于原点对称的单调区间内有相反的单调性.
2
热点聚焦 分类突破
热点一 函数及其表示
A.(1,2] B.(2,4] C.[1,2) D.[2,4)
B
D
综上,不等式f(x)≤5的解集为[-2,3].
1.(1)给出解析式的函数的定义域是使解析式有意义的自变量的集合,只需构建不等式(组)求解即可.
(2)抽象函数:根据f(g(x))中g(x)的范围与f(x)中x的范围相同求解.
2.对于分段函数求值或解不等式问题,一定要根据变量的取值条件进行分段讨论.
探究提高
A
解析 当x≥1时,f(x)=2x-1≥1,
热点二 函数的图象及应用
B
当x∈(0,1)时,ln|x|<0,x2+2>0,所以f(x)<0,排除D.故选B.
(2)已知函数f(x)=2x-x-1,则不等式f(x)>0的解集是( )
A.(-1,1) B.(-∞,-1)∪(1,+∞)
C.(0,1) D.(-∞,0)∪(1,+∞)
D
解析 在同一平面直角坐标系中画出h(x)=2x,g(x)=x+1的图象如图.由图象得交点坐标为(0,1)和(1,2).
又f(x)>0等价于2x>x+1,
结合图象,可得x<0或x>1.
故f(x)>0的解集为(-∞,0)∪(1,+∞).
1.函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不符合要求的图象.
2.(1)运用函数图象解决问题时,先要正确理解和把握函数图象本身的含义及其表示的内容,熟悉图象所能够表达的函数的性质.(2)图象形象地显示了函数的性质,因此,函数性质的确定与应用及一些方程、不等式的求解常与图象数形结合研究.
探究提高
A
所以f(x)是偶函数,图象关于y轴对称,排除C,D.
当0
解析 由图象可知不等式-2
所以0
热点三 函数的性质及应用
D
解析 由于f(x+1)为奇函数,所以函数f(x)的图象关于点(1,0)对称,
即有f(x)+f(2-x)=0,
所以f(1)+f(2-1)=0,得f(1)=0,即a+b=0 ①.
由于f(x+2)为偶函数,所以函数f(x)的图象关于直线x=2对称,
即有f(x)-f(4-x)=0,
所以f(0)+f(3)=-f(2)+f(1)=-4a-b+a+b=-3a=6 ②.
根据①②可得a=-2,b=2,
所以当x∈[1,2]时,f(x)=-2x2+2.
根据函数f(x)的图象关于直线x=2对称,且关于点(1,0)对称,可得函数f(x)的周期为4,
(2)(多选)已知函数f(x)的定义域为R,且f(x+1)是偶函数,f(x-1)是奇函数,则下列说法正确的是( )
A.f(7)=0 B.f(x)的一个周期为8
C.f(x)图象的一个对称中心为(3,0) D.f(x)图象的一条对称轴为直线x=2 019
ABC
解析 依题意知,直线x=1是f(x)图象的一条对称轴,(-1,0)是f(x)图象的一个对称中心,又因为f(x+1)是偶函数,f(x-1)是奇函数,所以f(x+1)=f(-x+1),f(x-1)=-f(-x-1),所以f(x)=f(-x+2),f(x)=-f(-x-2),所以f(-x+2)=-f(-x-2),所以f(x+2)=-f(x-2),所以f(x)=-f(x-4)=-[-f(x-8)]=f(x-8),所以f(x)是周期函数,且8为函数f(x)的一个周期,故B正确;
f(7)=f(-1)=0,故A正确;
因为f(x)图象上每隔4个单位长度出现一个对称中心,所以点(3,0)是函数f(x)图象的一个对称中心,故C正确;
x=2 019=8×252+3,所以直线x=2 019不是函数f(x)图象的对称轴,故D错误,故选ABC.
考向2 函数的单调性与奇偶性
AD
A.f(x)为奇函数 B.f(x)为偶函数
C.f(x)在R上单调递增 D.f(x)在R上单调递减
解析 由题意知函数f(x)的定义域为R,关于原点对称.对任意x∈R,
C
1.利用函数的奇偶性和周期性可以转化函数的解析式、图象和性质,把不在已知区间上的问题,转化到已知区间上求解.
2.函数单调性的应用:可以比较大小、求函数最值、解不等式、证明方程根的唯一性.
探究提高
【训练3】 (1)(2021·新高考Ⅱ卷)已知函数f(x)的定义域为R,f(x+2)为偶函数,f(2x+1)为奇函数,则( )
B
解析 因为函数f(x+2)为偶函数,则f(2+x)=f(2-x),可得f(x+3)=f(1-x).
因为函数f(2x+1)为奇函数,则f(1-2x)=-f(2x+1),
所以f(1-x)=-f(x+1),
所以f(x+3)=-f(x+1)=f(x-1),
即f(x)=f(x+4),
故函数f(x)是以4为周期的周期函数.
因为函数F(x)=f(2x+1)为奇函数,则F(0)=f(1)=0,故f(-1)=-f(1)=0,其它三个选项未知,不能确定数值.
(2)(2021·衡水模拟)已知定义在R上的可导函数f(x),对任意的实数x,都有f(x)-f(-x)=2x,且当x∈(0,+∞)时,f′(x)>1恒成立,若不等式f(a)-f(1-a)≥2a-1恒成立,则实数a的取值范围是( )
A
解析 由f(x)-f(-x)=2x,
得f(x)-x=f(-x)-(-x).
设F(x)=f(x)-x,则F(-x)=F(x),F(x)为偶函数.
由f′(x)>1,知F′(x)=f′(x)-1>0,
∴函数F(x)在(0,+∞)上单调递增.
由f(a)-f(1-a)≥2a-1,得f(a)-a≥f(1-a)-(1-a),
∴F(a)≥F(1-a) F(|a|)≥F(|1-a|),
专题训练 对接高考
3
巩固提升
一、选择题
1.(2021·北京卷)设函数f(x)的定义域为[0,1],则“函数f(x)在[0,1]上单调递增”是“函数f(x)在[0,1]上的最大值为f(1)”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
A
解析 显然f(-x)=-f(x),x∈[-π,π],所以f(x)为奇函数,排除A;
D
3.(2021·广州模拟)已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+a,则g(2)=( )
A.-4 B.4 C.-8 D.8
解析 依题意f(x)是偶函数,g(x)是奇函数,
且f(x)-g(x)=x3+x2+a,①
所以f(-x)-g(-x)=-x3+x2+a,
即f(x)+g(x)=-x3+x2+a,②
②-①得2g(x)=-2x3,g(x)=-x3,所以g(2)=-23=-8.故选C.
C
4.设f(x)是定义域为R的偶函数,且在(0,+∞)上单调递减,则( )
C
解析 因为f(x)是定义域为R的偶函数,
5.(多选)(2021·辽宁五校期末)定义在实数集R上的函数f(x)满足f(1+x)=-f(1-x),且x≥1时,函数f(x)单调递增,则( )
A.f(1)=0 B.f(x)是周期函数
C.方程f(x)=0有唯一实数解 D.函数f(x)在(-∞,0)上单调递减
AC
解析 ∵x∈R,f(1+x)=-f(1-x),
∴函数f(x)的图象关于点(1,0)成中心对称.
令x=0,则f(1)=-f(1),即f(1)=0.
又∵当x≥1时,函数f(x)单调递增,∴当x<1时,函数f(x)单调递增,∴f(x)不是周期函数,∴方程f(x)=0有唯一实数解.
∴A,C正确,B,D错误.故选AC.
6.设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)( )
D
又f(-x)=ln|-2x+1|-ln|-2x-1|=ln|2x-1|-ln|2x+1|=-f(x),
∴f(x)为奇函数,故排除A,C;
二、填空题
7.(2021·新高考Ⅰ卷)已知函数f(x)=x3(a·2x-2-x)是偶函数,则a=________.
1
解析 法一 因为f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数,
所以f(-x)=f(x)对任意的x∈R恒成立,
所以(-x)3(a·2-x-2x)=x3(a·2x-2-x)对任意的x∈R恒成立,
所以x3(a-1)(2x+2-x)=0对任意的x∈R恒成立,所以a=1.
法二 因为f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数,
经检验,f(x)=x3(2x-2-x)为偶函数,所以a=1.
法三 由题意知f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数.
设g(x)=x3,h(x)=a·2x-2-x,因为g(x)=x3为奇函数,
所以h(x)=a·2x-2-x为奇函数,
所以h(0)=a·20-2-0=0,解得a=1,
经检验,f(x)=x3(2x-2-x)为偶函数,所以a=1.
-ln 4
解析 ∵f(-1)=f(1),∴2-1=log2(1-a),
易知x<0时,f(x)=2x∈(0,1);
又x≥0时,f(x)=log2(x-a)递增,
故f(x)≥f(0)=log2(-a).
解得-1≤a<0.
10.设函数f(x)=ex+ae-x(a为常数).若f(x)为奇函数,则a=________;若f(x)是R上的增函数,则a的取值范围是________.
-1
(-∞,0]
解析 奇函数f(x)=ex+ae-x(a为常数)的定义域为R,
∴f(0)=e0+ae-0=1+a=0,∴a=-1(经验证符合题意).
∵f(x)是R上的增函数,∴f′(x)≥0在R上恒成立,
又e2x>0,∴a≤0,即a的取值范围是(-∞,0].
(1)求f(0);
(2)探究f(x)的单调性,并证明你的结论;
解 f(x)在R上单调递增,证明如下:
∵f(x)的定义域为R,∴任取x1,x2∈R且x1
∴f(x1)-f(x2)<0,即f(x1)
(3)若f(x)为奇函数,解不等式f(ax)
∴f(ax)
∴不等式的解集为(-∞,2).
能力突破
12.(多选)(2021·济南统考)设函数f(x)=min{|x-2|,x2,|x+2|},其中min{x,y,z}表示x,y,z中的最小者,则下列说法正确的是( )
A.函数f(x)为偶函数 B.当x∈[1,+∞)时,f(x-2)≤f(x)
C.当x∈R时,f(f(x))≤f(x) D.当x∈[-4,4]时,|f(x)-2|≥f(x)
ABC
解析 在同一平面直角坐标系中分别画出函数y=|x-2|,y=x2,y=|x+2|的图象如图所示,
显然f(-x)=f(x),故f(x)为偶函数,故A正确;
当x≥1时,f(x)=|x-2|,f(x-2)的图象可由f(x)的图象向右平移2个单位长度得到,显然当x≥1时,f(x)的图象不在f(x-2)图象的下方,即当x∈[1,+∞)时,f(x-2)≤f(x),故B正确;
由图可知,当x∈R时,f(x)≥0,令t=f(x),t≥0,由y=f(t)和y=t(t≥0)的图象可知,当t≥0时,直线y=t不在曲线y=f(t)的下方,所以当t≥0时,t≥f(t),即f(f(x))≤f(x),故C正确;
当x∈[-4,4]时,f(-4)=2,f(-4)-2=0,显然f(-4)>|f(-4)-2|,故D不正确.故选ABC.
解析 因为函数f(x)为奇函数,所以f(x)=-f(-x),
所以f(2-x)+f(x)=-f(x-2)+f(x)=0,
即f(x-2)=f(x),
所以f(x)是以2为周期的周期函数.
14.已知函数f(x+1)是定义在R上的偶函数, x1,x2∈[1,+∞),且x1≠x2,都有(x1-x2)[f(x2)-f(x1)]<0,则不等式f(-2x+1+1)<f(5)的解集为________.
(-∞,1)
解析 因为函数f(x+1)是定义在R上的偶函数,
所以f(x+1)的图象关于y轴对称.
因为f(x)的图象向左平移1个单位长度得到f(x+1)的图象,
所以f(x)的图象关于直线x=1对称.
因为 x1,x2∈[1,+∞),且x1≠x2,
都有(x1-x2)[f(x2)-f(x1)]<0,
所以函数f(x)在[1,+∞)上单调递增,
由此可得函数f(x)在(-∞,1)上单调递减.
因为f(-2x+1+1)<f(5),
且f(5)=f(-3),-2x+1+1<1,
所以-2x+1+1>-3,即2x+1<4,解得x<1,
所以所求不等式的解集为(-∞,1).
同课章节目录
