北师大版2022学年数学九年级下册期中检测卷(提高卷)(含答案)
文档属性
| 名称 | 北师大版2022学年数学九年级下册期中检测卷(提高卷)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 19:01:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2022学年数学九年级下册期中检测卷(提高卷)
一、单选题
1.在 中, ,如果 的正弦值是 ,那么下列各式正确的是( )
A. B. C. D.
2.下列函数是二次函数的是( )
A.y=x(x+1) B.x2y=1
C.y=2x2-2(x-1)2 D.y=x—0.5
3.对于抛物线y=(x﹣1)2+2的说法错误的是( )
A.抛物线的开口向上 B.抛物线的顶点坐标是(1,2)
C.抛物线与x轴无交点 D.当x<1时,y随x的增大而增大
4.将抛物线y=(x+1)2﹣3向右平移2个单位后得到的新抛物线的表达式为( )
A.y=(x﹣1)2﹣3 B.y=(x+3)2﹣3
C.y=(x+1)2﹣1 D.y=(x+1)2﹣5
5.如图,将 绕点A按顺时针方向旋转一定角度得到 ,点B的对应点D恰好落在 边上.若 ,则 的长为( ) 21教育网
( http: / / www.21cnjy.com / )
A.0.5 B.1.5 C. D.1
6.如图,小明家附近有一观光塔CD,他发现当光线角度发生变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他继续往前再走5米到达点B(点A,B,C在同一直线上),此时塔顶D的仰角为53°,则观光塔CD的高度约为( )(精确到0.1米,参考数值: , ) 21cnjy.com
( http: / / www.21cnjy.com / )
A.7.6米 B.7.8米 C.8.6米 D.8.8米
7.将抛物线 向上平移 个单位后得到的抛物线恰好与 轴有一个交点,则a的值为( ) www.21-cn-jy.com
A.-1 B.1 C.-2 D.2
8.如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是( )
( http: / / www.21cnjy.com / )
A.50° B.55° C.60° D.65°
9.如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. B. C. D.
10.已知抛物线y=a(x﹣3)2+过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切。正确的结论是( )
( http: / / www.21cnjy.com / )
A.①③ B.①④ C.①③④ D.①②③④
二、填空题
11.如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,则sinA= .
( http: / / www.21cnjy.com / )
12.若点,在抛物线上,则,的大小关系为: (填“>”,“=”或“<”).www-2-1-cnjy-com
13.请选择一组你喜欢的 、 、 的值,使二次函数 的图象同时满足下列条件:①开口向下,②对称轴是直线 ;③顶点在 轴下方,这样的二次函数的解析式可以是 .2-1-c-n-j-y
14.如图,⊙O的半径是5,点A在⊙O上.P是⊙O所在平面内一点,且AP=2,过点P作直线l,使l⊥PA.21*cnjy*com
(1)点O到直线l距离的最大值为 ;
(2)若M,N是直线l与⊙O的公共点,则当线段MN的长度最大时,OP的长为 .
( http: / / www.21cnjy.com / )
15.如图,有一座抛物线 ( http: / / www.21cnjy.com )形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就到达警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升 小时水位能由正常水位到达拱桥顶.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
16.如图,点A、B、C、D在⊙O上,AD是⊙O的直径,且AD=3 ,若∠ABC=∠CAD,BC交AD于点E,则CE BC为 . 21教育名师原创作品
( http: / / www.21cnjy.com / )
三、解答题
17.把二次函数y=﹣2x2﹣4x+5化成y=a(x-h)2+k形式,并求出它的图象顶点坐标、对称轴
18.如图, 的弦 相交于点P,且 .求证 .
( http: / / www.21cnjy.com / )
19.如图,在楼房AB和 ( http: / / www.21cnjy.com )塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)21·cn·jy·com
( http: / / www.21cnjy.com / )
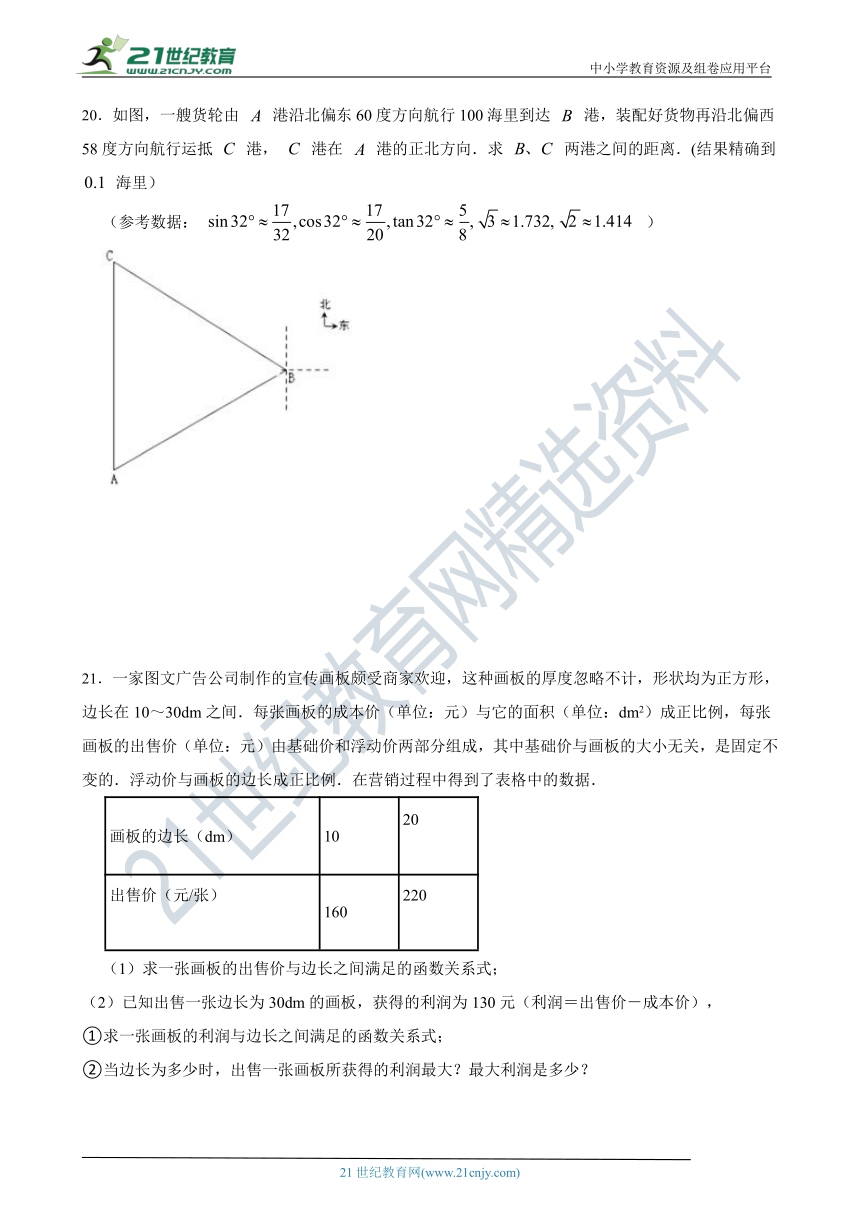
20.如图,一艘货轮由 港沿北偏东60度方向航行100海里到达 港,装配好货物再沿北偏西58度方向航行运抵 港, 港在 港的正北方向.求 两港之间的距离.(结果精确到 海里) 21*cnjy*com
(参考数据: )
( http: / / www.21cnjy.com / )
21.一家图文广告公司制作的宣传画板颇受商家 ( http: / / www.21cnjy.com )欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.【出处:21教育名师】
画板的边长(dm) 10 20
出售价(元/张)
160 220
(1)求一张画板的出售价与边长之间满足 ( http: / / www.21cnjy.com )的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?2·1·c·n·j·y
22.在体育课掷实心球活动中,小华通过研究发现:实心球所经过的路线是一条抛物线的一部分,如果球出手处点 距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问实心球的落地点 与出手处点 的水平距离是多少?(结果保留根号)
( http: / / www.21cnjy.com / )
23.某机械传动装置在静止时如图,连杆PB与 ( http: / / www.21cnjy.com )点B运动所形成的⊙O交于点A,测得PA=4cm,AB=6cm,⊙O半径为5cm,求点P到圆心O的距离. 【版权所有:21教育】
( http: / / www.21cnjy.com / )
24.已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
( http: / / www.21cnjy.com / )
(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】
12.【答案】<
13.【答案】 (不唯一)
14.【答案】(1)7
(2)
15.【答案】20
16.【答案】9
17.【答案】解:y=-2 ( http: / / www.21cnjy.com )x2-4x+5=-2(x2+2x+1-1)+5=-2(x+1)2+7.
∴顶点坐标为(-1,7),对称轴为直线x=-1.【来源:21·世纪·教育·网】
18.【答案】证明:连接BD.
( http: / / www.21cnjy.com / )
∴
即
19.【答案】解:如图, ( http: / / www.21cnjy.com / )由题意可知∠BAD=∠ADB=45°,∴FD=EF=6米,在Rt△PEH中,∵tanβ= ,∴BF= ,∴PG=BD=BF+FD=5 +6,在Rt△PCG中,∵tanβ= ,∴CG=(5 +6) =5+2 ,∴CD=(6+2 )米.
20.【答案】解:过点B作BD⊥AC,垂足为D,
( http: / / www.21cnjy.com / )
在Rt△ABD中,
∵ ,
,
∵∠CBE=58°,
∴∠DBC=32°,
在 ,
∴ 海里
答: 两刚之间距离101.9海里.
21.【答案】(1)设正方形画板的边长为xdm,出售价为每张y元,且y=kx+b(k≠0) (1分)
由表格中的数据可得,,解得
从而一张画板的出售价y与边长x之间满足函数关系式y=6x+100
(2)设每张画板的成本价为ax2,利润W=6x+100-ax2
当x=30时,W=130,180+100-900a=130,得a=
一张画板的利润W与边长x之间满足函数关系式W=-x2+6x+100
由W=-16(x-18)2+154,知当x=18时,W有最大值,W最大=154
因此当正方形画板的边长为18dm时,可获最大利润154元.21·世纪*教育网
22.【答案】解:建立平面直角坐标系,如图所示.
( http: / / www.21cnjy.com / )
则 ,
设抛物线解析式为 ( ),
在抛物线上,
代入得: ,
.
令 ,
(舍), ,
.
答:实心球的落地点 与出手处点 的水平距离是 .
23.【答案】解:连接OA,过点O作OD⊥AB于点D,
∵AB=6cm,
∴AD=BD= AB=3,
∴PD=PA+AD=4+3=7.
在Rt△AOD中,
∵OA=5,
∴OD= = =4.
在Rt△OPD中,OP= = = .
( http: / / www.21cnjy.com / )
24.【答案】解:(Ⅰ)∵MA切⊙O于点A,∴∠MAC=90°.
又∠BAC=25°,∴∠MAB=∠MAC-∠BAC=65°.
∵MA、MB分别切⊙O于点A、B,∴MA=MB.
∴∠MAB=∠MBA.
∴∠AMB=180°-(∠MAB+∠MBA)=50°.
(Ⅱ)如图,连接AD、AB,
( http: / / www.21cnjy.com / )
∵MA⊥AC,又BD⊥AC,
∴BD∥MA.
又∵BD=MA,∴四边形MADB是平行四边形.
又∵MA=MB,∴四边形MADB是菱形.∴AD=BD.
又∵AC为直径,AC⊥BD,
∴ AB =" AD" .
∴AB=AD=BD.∴△ABD是等边三角形.∴∠D=60°.
∴在菱形MADB中,∠AMB=∠D=60°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版2022学年数学九年级下册期中检测卷(提高卷)
一、单选题
1.在 中, ,如果 的正弦值是 ,那么下列各式正确的是( )
A. B. C. D.
2.下列函数是二次函数的是( )
A.y=x(x+1) B.x2y=1
C.y=2x2-2(x-1)2 D.y=x—0.5
3.对于抛物线y=(x﹣1)2+2的说法错误的是( )
A.抛物线的开口向上 B.抛物线的顶点坐标是(1,2)
C.抛物线与x轴无交点 D.当x<1时,y随x的增大而增大
4.将抛物线y=(x+1)2﹣3向右平移2个单位后得到的新抛物线的表达式为( )
A.y=(x﹣1)2﹣3 B.y=(x+3)2﹣3
C.y=(x+1)2﹣1 D.y=(x+1)2﹣5
5.如图,将 绕点A按顺时针方向旋转一定角度得到 ,点B的对应点D恰好落在 边上.若 ,则 的长为( ) 21教育网
( http: / / www.21cnjy.com / )
A.0.5 B.1.5 C. D.1
6.如图,小明家附近有一观光塔CD,他发现当光线角度发生变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他继续往前再走5米到达点B(点A,B,C在同一直线上),此时塔顶D的仰角为53°,则观光塔CD的高度约为( )(精确到0.1米,参考数值: , ) 21cnjy.com
( http: / / www.21cnjy.com / )
A.7.6米 B.7.8米 C.8.6米 D.8.8米
7.将抛物线 向上平移 个单位后得到的抛物线恰好与 轴有一个交点,则a的值为( ) www.21-cn-jy.com
A.-1 B.1 C.-2 D.2
8.如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是( )
( http: / / www.21cnjy.com / )
A.50° B.55° C.60° D.65°
9.如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. B. C. D.
10.已知抛物线y=a(x﹣3)2+过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切。正确的结论是( )
( http: / / www.21cnjy.com / )
A.①③ B.①④ C.①③④ D.①②③④
二、填空题
11.如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,则sinA= .
( http: / / www.21cnjy.com / )
12.若点,在抛物线上,则,的大小关系为: (填“>”,“=”或“<”).www-2-1-cnjy-com
13.请选择一组你喜欢的 、 、 的值,使二次函数 的图象同时满足下列条件:①开口向下,②对称轴是直线 ;③顶点在 轴下方,这样的二次函数的解析式可以是 .2-1-c-n-j-y
14.如图,⊙O的半径是5,点A在⊙O上.P是⊙O所在平面内一点,且AP=2,过点P作直线l,使l⊥PA.21*cnjy*com
(1)点O到直线l距离的最大值为 ;
(2)若M,N是直线l与⊙O的公共点,则当线段MN的长度最大时,OP的长为 .
( http: / / www.21cnjy.com / )
15.如图,有一座抛物线 ( http: / / www.21cnjy.com )形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就到达警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升 小时水位能由正常水位到达拱桥顶.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
16.如图,点A、B、C、D在⊙O上,AD是⊙O的直径,且AD=3 ,若∠ABC=∠CAD,BC交AD于点E,则CE BC为 . 21教育名师原创作品
( http: / / www.21cnjy.com / )
三、解答题
17.把二次函数y=﹣2x2﹣4x+5化成y=a(x-h)2+k形式,并求出它的图象顶点坐标、对称轴
18.如图, 的弦 相交于点P,且 .求证 .
( http: / / www.21cnjy.com / )
19.如图,在楼房AB和 ( http: / / www.21cnjy.com )塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)21·cn·jy·com
( http: / / www.21cnjy.com / )
20.如图,一艘货轮由 港沿北偏东60度方向航行100海里到达 港,装配好货物再沿北偏西58度方向航行运抵 港, 港在 港的正北方向.求 两港之间的距离.(结果精确到 海里) 21*cnjy*com
(参考数据: )
( http: / / www.21cnjy.com / )
21.一家图文广告公司制作的宣传画板颇受商家 ( http: / / www.21cnjy.com )欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.【出处:21教育名师】
画板的边长(dm) 10 20
出售价(元/张)
160 220
(1)求一张画板的出售价与边长之间满足 ( http: / / www.21cnjy.com )的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?2·1·c·n·j·y
22.在体育课掷实心球活动中,小华通过研究发现:实心球所经过的路线是一条抛物线的一部分,如果球出手处点 距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问实心球的落地点 与出手处点 的水平距离是多少?(结果保留根号)
( http: / / www.21cnjy.com / )
23.某机械传动装置在静止时如图,连杆PB与 ( http: / / www.21cnjy.com )点B运动所形成的⊙O交于点A,测得PA=4cm,AB=6cm,⊙O半径为5cm,求点P到圆心O的距离. 【版权所有:21教育】
( http: / / www.21cnjy.com / )
24.已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
( http: / / www.21cnjy.com / )
(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】
12.【答案】<
13.【答案】 (不唯一)
14.【答案】(1)7
(2)
15.【答案】20
16.【答案】9
17.【答案】解:y=-2 ( http: / / www.21cnjy.com )x2-4x+5=-2(x2+2x+1-1)+5=-2(x+1)2+7.
∴顶点坐标为(-1,7),对称轴为直线x=-1.【来源:21·世纪·教育·网】
18.【答案】证明:连接BD.
( http: / / www.21cnjy.com / )
∴
即
19.【答案】解:如图, ( http: / / www.21cnjy.com / )由题意可知∠BAD=∠ADB=45°,∴FD=EF=6米,在Rt△PEH中,∵tanβ= ,∴BF= ,∴PG=BD=BF+FD=5 +6,在Rt△PCG中,∵tanβ= ,∴CG=(5 +6) =5+2 ,∴CD=(6+2 )米.
20.【答案】解:过点B作BD⊥AC,垂足为D,
( http: / / www.21cnjy.com / )
在Rt△ABD中,
∵ ,
,
∵∠CBE=58°,
∴∠DBC=32°,
在 ,
∴ 海里
答: 两刚之间距离101.9海里.
21.【答案】(1)设正方形画板的边长为xdm,出售价为每张y元,且y=kx+b(k≠0) (1分)
由表格中的数据可得,,解得
从而一张画板的出售价y与边长x之间满足函数关系式y=6x+100
(2)设每张画板的成本价为ax2,利润W=6x+100-ax2
当x=30时,W=130,180+100-900a=130,得a=
一张画板的利润W与边长x之间满足函数关系式W=-x2+6x+100
由W=-16(x-18)2+154,知当x=18时,W有最大值,W最大=154
因此当正方形画板的边长为18dm时,可获最大利润154元.21·世纪*教育网
22.【答案】解:建立平面直角坐标系,如图所示.
( http: / / www.21cnjy.com / )
则 ,
设抛物线解析式为 ( ),
在抛物线上,
代入得: ,
.
令 ,
(舍), ,
.
答:实心球的落地点 与出手处点 的水平距离是 .
23.【答案】解:连接OA,过点O作OD⊥AB于点D,
∵AB=6cm,
∴AD=BD= AB=3,
∴PD=PA+AD=4+3=7.
在Rt△AOD中,
∵OA=5,
∴OD= = =4.
在Rt△OPD中,OP= = = .
( http: / / www.21cnjy.com / )
24.【答案】解:(Ⅰ)∵MA切⊙O于点A,∴∠MAC=90°.
又∠BAC=25°,∴∠MAB=∠MAC-∠BAC=65°.
∵MA、MB分别切⊙O于点A、B,∴MA=MB.
∴∠MAB=∠MBA.
∴∠AMB=180°-(∠MAB+∠MBA)=50°.
(Ⅱ)如图,连接AD、AB,
( http: / / www.21cnjy.com / )
∵MA⊥AC,又BD⊥AC,
∴BD∥MA.
又∵BD=MA,∴四边形MADB是平行四边形.
又∵MA=MB,∴四边形MADB是菱形.∴AD=BD.
又∵AC为直径,AC⊥BD,
∴ AB =" AD" .
∴AB=AD=BD.∴△ABD是等边三角形.∴∠D=60°.
∴在菱形MADB中,∠AMB=∠D=60°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
