高三数学高考专题训练:圆锥曲线最值问题公开课课件(共22张PPT)
文档属性
| 名称 | 高三数学高考专题训练:圆锥曲线最值问题公开课课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 329.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 12:03:57 | ||
图片预览





文档简介
(共22张PPT)
圆锥曲线的最值问题
高三复习专题教学
高考地位:
最值问题是高考的热点,而圆锥曲线的最值问题几乎是高考的必考点,不仅会在选择题或填空题中进行考察,在综合题中也往往将其设计为试题考查的核心。
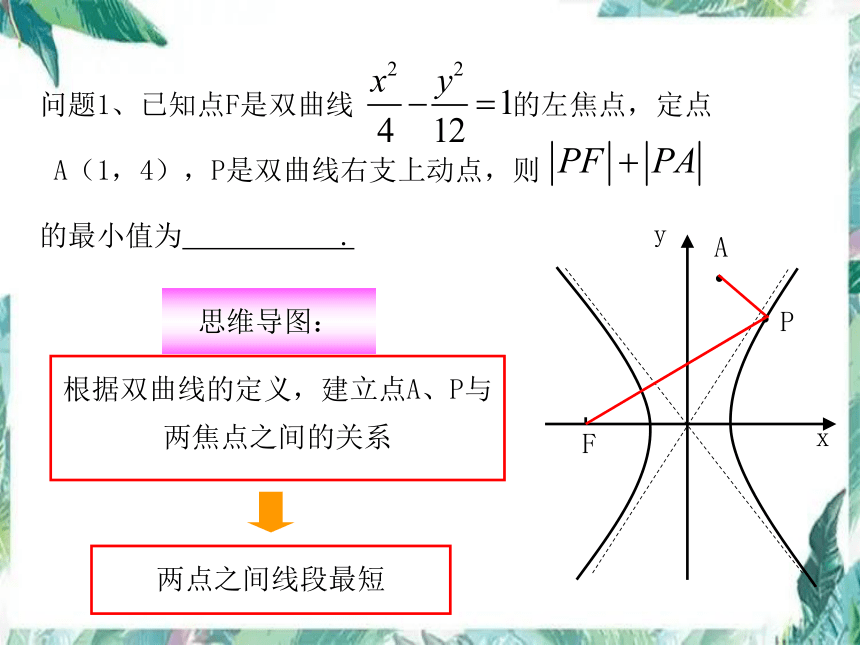
问题1、已知点F是双曲线 的左焦点,定点
A(1,4),P是双曲线右支上动点,则
的最小值为 .
思维导图:
根据双曲线的定义,建立点A、P与两焦点之间的关系
两点之间线段最短
F
A
P
y
x
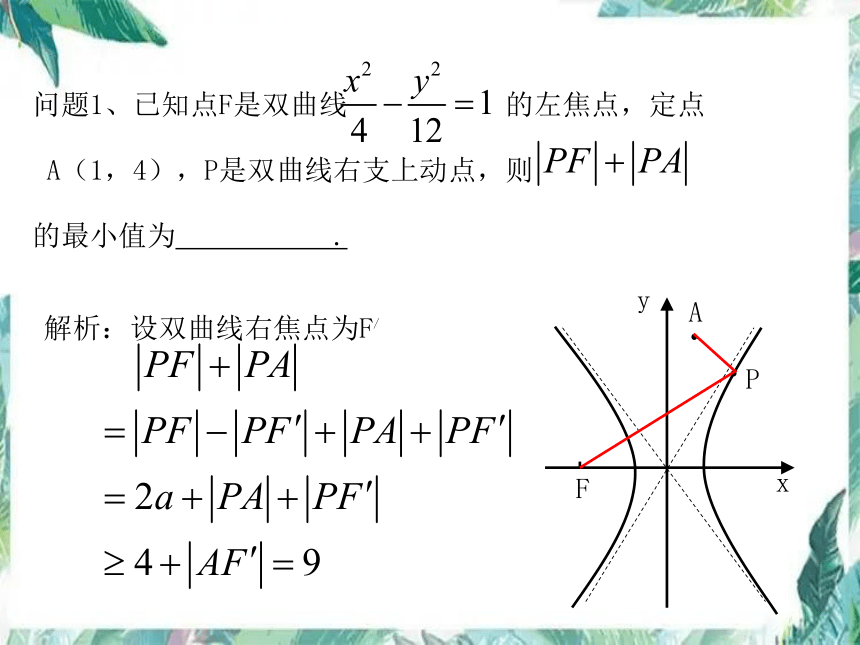
问题1、已知点F是双曲线 的左焦点,定点
A(1,4),P是双曲线右支上动点,则
的最小值为 .
解析:设双曲线右焦点为F/
F
A
P
y
x
方法总结1:
圆锥曲线的定义转化法
根据圆锥曲线的定义,把所求的最值转化为平面上两点之间的距离、点线之间的距离等,这是求圆锥曲线最值问题的基本方法。
关键:用好圆锥曲线的定义
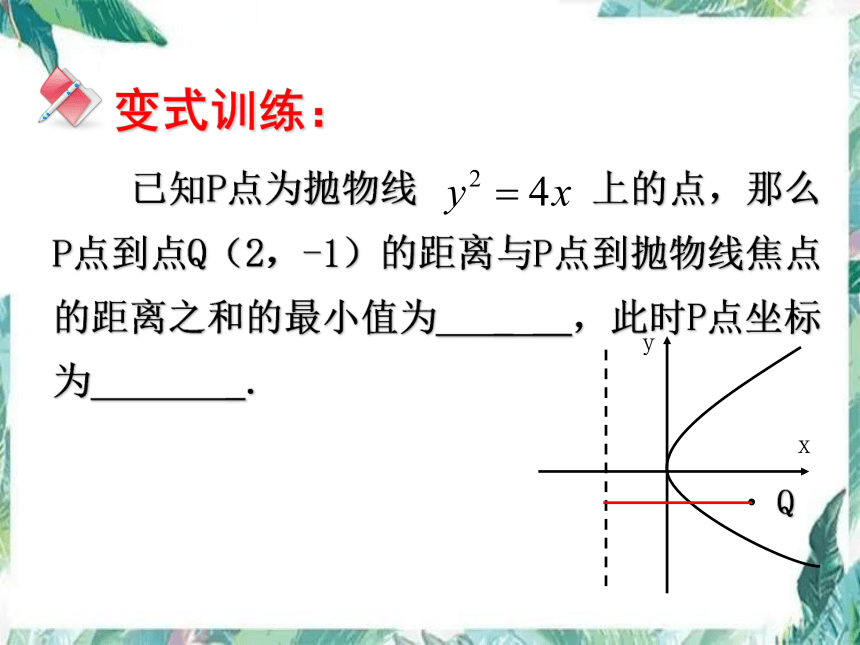
变式训练:
已知P点为抛物线 上的点,那么P点到点Q(2,-1)的距离与P点到抛物线焦点的距离之和的最小值为 _ __,此时P点坐标为 _.
Q
x
y
回顾反思与能力提升:
1、若圆锥曲线为椭圆,A为椭圆内一点,有可
得出什么结论,能否自己设计出一道题目;
2、体现了什么数学思想方法?
3、理论根据是什么?
4、此法适合解决那类问题?
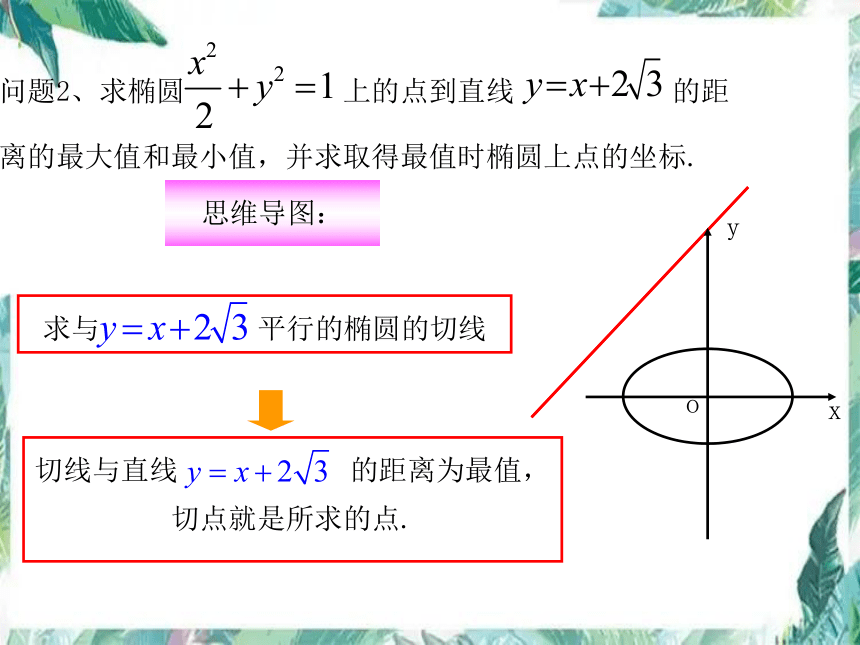
问题2、求椭圆 上的点到直线 的距
离的最大值和最小值,并求取得最值时椭圆上点的坐标.
思维导图:
求与 平行的椭圆的切线
切线与直线 的距离为最值,切点就是所求的点.
x
y
o
问题2、求椭圆 上的点到直线 的距
离的最大值和最小值,并求取得最值时椭圆上点的坐标.
解:设椭圆与 平行的切线方程为
方法总结2:
切 线 法
当所求的最值是圆锥曲线上点到某条直线的距离的最值时,可以通过作与这条直线平行的圆锥曲线的切线,则两平行线间的距离就是所求的最值,切点就是曲线上去的最值时的点。
变式训练:
动点P在抛物线 上,则点P
到直线 的距离最小时,P点的坐
标为_________.
回顾反思与能力提升:
1、此法用了哪种数学思想方法?
2、有没有别的办法?
3、要注意画出草图,根据图形确定何时取最大
值,何时取最小值.
问题3: 直线 与椭圆 交于A、B两点,直线 与椭圆交于C、D两点,求四边形ABCD的面积。
A
B
C
D
思维导图:
用k表示四边形的面积
根据函数或基本不等式求最值
思考题:设椭圆中心在坐标原点A(2,0)、B(0,1)是它的两个顶点,直线 与椭圆交于E、F两点,求四边形AEBF面积的最大值.
A
F
E
B
x
y
问题3、设椭圆中心在坐标原点A(2,0)、B(0,1)是它的两个顶点,直线 与椭圆交于E、F两点,求四边形AEBF面积的最大值.
解析:依题意设得椭圆标准方程为
直线AB、EF的方程分别为
设
根据点到直线距离公式及上式,点E、F到AB的距离分别为
∴四边形AFBE的面积为
方法总结3:
构造函数,妙用基本不等式法
先将所求最值的量用变量表示出来,再利
用基本不等式求这个表达式的最值.
这种方法是求圆锥曲线中最值问题应用最
为广泛的一种方法.
变式训练:
已知椭圆 的左右焦点
分别为F1、F2,过F1的直线交椭圆于B、D
两点,过F2的直线交椭圆于A、C两点,且
AC⊥BD,求四边形ABCD面积的最小值.
回顾反思与能力提升:
1、关键是什么?
2、应注意什么?
作业:
小结:
圆锥曲线的最值问题解决方法较多,有些题目可以用多种方法解决,遇到此类题目时,要选取适当地方法。
谢谢
圆锥曲线的最值问题
高三复习专题教学
高考地位:
最值问题是高考的热点,而圆锥曲线的最值问题几乎是高考的必考点,不仅会在选择题或填空题中进行考察,在综合题中也往往将其设计为试题考查的核心。
问题1、已知点F是双曲线 的左焦点,定点
A(1,4),P是双曲线右支上动点,则
的最小值为 .
思维导图:
根据双曲线的定义,建立点A、P与两焦点之间的关系
两点之间线段最短
F
A
P
y
x
问题1、已知点F是双曲线 的左焦点,定点
A(1,4),P是双曲线右支上动点,则
的最小值为 .
解析:设双曲线右焦点为F/
F
A
P
y
x
方法总结1:
圆锥曲线的定义转化法
根据圆锥曲线的定义,把所求的最值转化为平面上两点之间的距离、点线之间的距离等,这是求圆锥曲线最值问题的基本方法。
关键:用好圆锥曲线的定义
变式训练:
已知P点为抛物线 上的点,那么P点到点Q(2,-1)的距离与P点到抛物线焦点的距离之和的最小值为 _ __,此时P点坐标为 _.
Q
x
y
回顾反思与能力提升:
1、若圆锥曲线为椭圆,A为椭圆内一点,有可
得出什么结论,能否自己设计出一道题目;
2、体现了什么数学思想方法?
3、理论根据是什么?
4、此法适合解决那类问题?
问题2、求椭圆 上的点到直线 的距
离的最大值和最小值,并求取得最值时椭圆上点的坐标.
思维导图:
求与 平行的椭圆的切线
切线与直线 的距离为最值,切点就是所求的点.
x
y
o
问题2、求椭圆 上的点到直线 的距
离的最大值和最小值,并求取得最值时椭圆上点的坐标.
解:设椭圆与 平行的切线方程为
方法总结2:
切 线 法
当所求的最值是圆锥曲线上点到某条直线的距离的最值时,可以通过作与这条直线平行的圆锥曲线的切线,则两平行线间的距离就是所求的最值,切点就是曲线上去的最值时的点。
变式训练:
动点P在抛物线 上,则点P
到直线 的距离最小时,P点的坐
标为_________.
回顾反思与能力提升:
1、此法用了哪种数学思想方法?
2、有没有别的办法?
3、要注意画出草图,根据图形确定何时取最大
值,何时取最小值.
问题3: 直线 与椭圆 交于A、B两点,直线 与椭圆交于C、D两点,求四边形ABCD的面积。
A
B
C
D
思维导图:
用k表示四边形的面积
根据函数或基本不等式求最值
思考题:设椭圆中心在坐标原点A(2,0)、B(0,1)是它的两个顶点,直线 与椭圆交于E、F两点,求四边形AEBF面积的最大值.
A
F
E
B
x
y
问题3、设椭圆中心在坐标原点A(2,0)、B(0,1)是它的两个顶点,直线 与椭圆交于E、F两点,求四边形AEBF面积的最大值.
解析:依题意设得椭圆标准方程为
直线AB、EF的方程分别为
设
根据点到直线距离公式及上式,点E、F到AB的距离分别为
∴四边形AFBE的面积为
方法总结3:
构造函数,妙用基本不等式法
先将所求最值的量用变量表示出来,再利
用基本不等式求这个表达式的最值.
这种方法是求圆锥曲线中最值问题应用最
为广泛的一种方法.
变式训练:
已知椭圆 的左右焦点
分别为F1、F2,过F1的直线交椭圆于B、D
两点,过F2的直线交椭圆于A、C两点,且
AC⊥BD,求四边形ABCD面积的最小值.
回顾反思与能力提升:
1、关键是什么?
2、应注意什么?
作业:
小结:
圆锥曲线的最值问题解决方法较多,有些题目可以用多种方法解决,遇到此类题目时,要选取适当地方法。
谢谢
同课章节目录
