第1讲 空间几何体与空间位置关系——小题备考 课件(共张35PPT)
文档属性
| 名称 | 第1讲 空间几何体与空间位置关系——小题备考 课件(共张35PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 00:59:17 | ||
图片预览











文档简介
(共35张PPT)
第1讲 空间几何体与空间位置关系——小题备考
微专题1 空间几何体的表面积和体积
微专题2 与球有关的切、接问题
微专题3 空l间中的位置关系
微专题1
空间几何体的表面积和体积
『常考常用结论』
1.柱体、锥体、台体、球的表面积公式:
①圆柱的表面积S=2πr(r+l);
②圆锥的表面积 S=πr(r+l);
③圆台的表面积S=π(r′2+r2+r′l+rl);
④球的表面积S=4πR2.
2.柱体、锥体和球的体积公式:
①V柱体=Sh(S为底面面积,h为高);
②V锥体=Sh(S为底面面积,h为高);
③V球=πR3.
『保分题组训练』
1.[2021·广东大联考]正方体ABCD-A1B1C1D1的棱长为2,E为BC的中点,则四面体AEDC1的体积为( )
A.4 B. C. D.2
C
解析:由题意,四面体AEDC1的底面积为:×2×2=2,高为2,
所以四面体AEDC1的体积为:×2×2=.
故选C.
2.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12π B.12π C.8π D.10π
B
解析:设圆柱的底面半径为r,由题意得高h=2r,
∴(2r)2=8,得r=,
∴S圆柱表=2πr2+2πrh=4π+8π=12π.故选B.
3.[2021·福建福州二模]某公园设置了一些石凳供大家休息,每张石凳是由正方体石料截去八个一样的四面体得到的,如图所示.如果一张石凳的体积是0.18 m3,那么原正方体石料的体积是( )
A.0.196 m3 B.0.216 m3
C.0.225 m3 D.0.234 m3
解析:设正方体的棱长为a,则正方体的体积为a3,
每一个正四面体的体积为:····=,
由题意可知:a3-8·=0.18 a3=0.216,故选B.
B
4.[2021·山东淄博一模]已知某圆锥底面圆的半径r=1,侧面展开图
是一个半圆,则此圆锥的体积为________.
解析:∵圆锥的侧面展开图是一个半圆,圆锥的底面周长为:2π,即侧面展开图半圆的弧长是2π,半圆的半径就是圆锥的母线:2,
圆锥的高为:=,
∴圆锥的体积=π·12·=.
『提分题组训练』
1. [2021·湖北五校联考]某班科技兴趣小组研究在学校的图书馆顶上安装太阳能板的发电量问题,要测量顶部的面积,将图书馆看成是一个长方体与一个等底的正四棱锥组合而成,经测量长方体的底面正方形的边长为26米,高为9米,当正四棱锥的顶点在阳光照射下的影子恰好落在底面正方形的对角线的延长线上时,测的光线与底面夹角为30°,正四棱锥顶点的影子到长方体下底面最近顶点的距离为11.8米,则图书馆顶部的面积大约为________平方米(注:≈1.4,≈1.7,≈15.2)( )
A.990 B.890 C.790 D.690
C
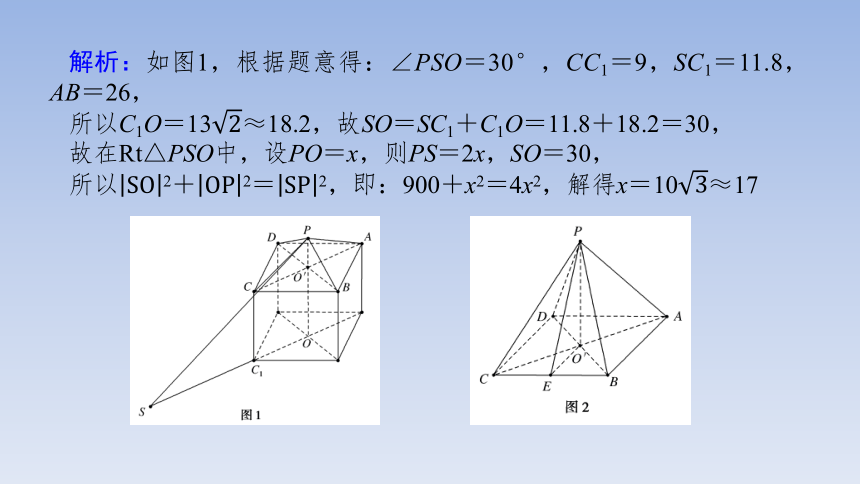
解析:如图1,根据题意得:∠PSO=30°,CC1=9,SC1=11.8,AB=26,
所以C1O=13≈18.2,故SO=SC1+C1O=11.8+18.2=30,
故在Rt△PSO中,设PO=x,则PS=2x,SO=30,
所以2+2=2,即:900+x2=4x2,解得x=10≈17
所以如图2,在正四棱锥P-ABCD中,PO′=17-9=8,AB=26,
取BC中点E,连接EP,EO′,所以EO′=13
由正四棱锥的性质得△PEO为直角三角形,故2=2+2=132+82=233,
所以=≈15.2,
所以正四棱锥P-ABCD的侧面积为S=4×S△PBC=4××15.2×26=790.4≈790.故选C.
2.[2021·湖南永州三模] 有一个装有水且底面直径为12 cm的圆柱形容器,水面与容器口的距离为1 cm.现往容器中放入一个半径为r(单位:cm)的小球,该小球放入水中后直接沉入容器底部,若使该容器内的水不溢出,则小球半径r的最大值为( )
A.1 B. 2 C. 3 D. 4
解析:小球放入水中后直接沉入容器底部,若使该容器内的水不溢出,则球的最大体积与圆柱上部的体积相等,小球半径r,
可得·r3=62π·1,
解得r=3(cm).故选C.
C
3.[2021·辽宁沈阳三模]柏拉图多面体,是指严格对称,结构等价的正多面体,由于太完美,因此数量很少,只有正四、六、八、十二、二十面体五种,如果用边数不同的正多边形来构造接近圆球、比较完美的多面体,那么数量会多一些,用两种或两种以上的正多边形构建的凸多面体虽不是正多面体,但有些类似,这样的多面体叫做半正多面体,古希腊数学家、物理学家阿基米德对这些正多面体进行研究并发现了13种半正多面体(后人称为“阿基米德多面体”).现在正四面体上将四个角各截去一角,形成最简单的阿基米德多面体家族中的一个,又名截角四面体.设原正四面体的棱长为6,则所得的截角四面体的体积为( )
A. B. C. D.18
C
解析:由题意及几何体的对称性可知,所得截角四面体为棱长为6的正四面体截掉四个棱长为2的正四面体而构成的几何图形.设一个棱长为x的正四面体的体积为V(x),可求得正四面体的高为=x,正四面体一个底面正三角形的面积为x2sin 60°=x2,V(x)=x×x2=x3.可得V(6)=×216=18,V(2)=×8=,故所得截角四面体的体积为18-4×=.故选C.
4.[2021·河北沧州二模]沙漏是一种古代的计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时,如图,某沙漏由上、下两个圆锥组成,该圆锥的高为1,若上面的圆锥中装有高度为的液体,且液体能流入下面的圆锥,
则液体流下去后的液面高度为________.
解析:=3=,当液体流下去后,=1-=,所以液体流下去后的液面高度为1-.
1-
【技法领悟】
求解几何体的表面积和体积的技巧
1.求几何体的表面积及体积问题,可以多角度、多方位地考虑,熟记公式是关键.求三棱锥的体积,等体积转化是常用的方法,转化原则是其高易求,底面放在已知几何体的某一面上.
2.求不规则几何体的体积,常用分割或补形的方法,将不规则几何体转化为规则几何体,易于求解.
微专题2
与球有关的切、和接的问题
『常考常用结论』
1.球的表面积S=4πR2,体积V=πR3.
2.长方体、正方体的体对角线等于其外接球的直径.
3.n面体的表面积为S,体积为V,则内切球的半径r=.
4.直三棱柱的外接球半径:R=,其中r为底面三角形的外接圆半径,L为侧棱长,如果直三棱柱有内切球,则内切球半径R′=.
5.正四面体中,外接球和内切球的球心重合,且球心在高对应的线段上,它是高的四等分点,球心到顶点的距离为外接球的半径R=a,球心到底面的距离为内切球的半径r=a,因此R∶r=3∶1.
『保分题组训练』
1.[2020·天津卷]若棱长为2的正方体的顶点都在同一球面上,则该球的表面积为( )
A.12π B.24π C.36π D.144π
解析:设外接球的半径为R,易知2R=×2=6,所以R=3,于是表面积S=4πR2=36π,故选C.
C
2.设正方体的表面积为24,那么其内切球的体积是( )
A. B.π C. D.
解析:设正方体的棱长为a,
则6a2=24,解得a=2,
所以正方体的内切球的半径为1,
其体积为×13=.
故选A.
A
3.[2021·山东泰安一模]设三棱柱的侧棱垂直于底面,所有棱的长都为1,顶点都在一个球面上,则该球的表面积为( )
A.5π B.π C.π D.π
解析:根据题意条件可知三棱柱是棱长都为1的正三棱柱,上下底面中心连线的中点就是球心,
则其外接球的半径为R==,
则球的表面积为S=4π×=,
故选D.
D
4.[2021·辽宁朝阳二模]已知三棱锥S-ABC的三条侧棱SA,SB,SC两两互相垂直且AC=,AB=,此三棱锥的外接球的表面积为14π,则BC=_______.
4.解析:设SA=x,SB=y,SC=z,
由题意可得:x2+z2=13,x2+y2=5,y2+z2=BC2,
三棱锥的外接球的表面积为14π,三棱锥扩展为长方体,长方体的对角线的长度,就是外接球的直径2R,
所以2R=,4πR2=14π,
可得x2+y2+z2=14,
解得x=2,y=1,z=3,
所以BC==.
『提分题组训练』
1.[2021·山东临沂二模]如图为一个圆锥形的金属配件,重75.06克,其正视图是一个等边三角形,现将其打磨成一个体积最大的球形配件,则该球形配件的重量约为( )
A.32.69克 B.33.36克 C.34.03克 D.34.37克
解析:设圆锥形的体积为V1,底面半径为r,内切球的体积为V2,
∴V1=··2r,V2=π3,
∴= = m=33.36,
故选B.
B
2.[2021·河北沧州二模]在三棱锥P-ABC中,底面ABC是面积为3的正三角形,若三棱锥P-ABC的每个顶点都在球O的球面上,且点O恰好在平面ABC内,则三棱锥P-ABC体积的最大值为( )
A. B.2 C.4 D.6
解析:由题可知底面ABC的边长为2,因为三棱锥P-ABC外接球的球心O恰好在平面ABC内,所以球O的半径为2,则三棱锥P-ABC体积的最大值为×3×2=2.
故选B.
B
3.[2021·山东德州一模]已知三棱锥P-ABC中,AP,AB,AC三条棱两两垂直,且长度均为2,以顶点P为球心,4为半径作一个球,则该球面被三棱锥四个表面截得的所有弧长之和为________.
解析:如图,AP=2,PN=4,则AN=2,∠APN=,
∴∠NPM==,
∴=×4=,同理=,
=×2=π,=×4=,
故球面与三棱锥的表面相交所得到的四段弧长之和等于+π+=3π,
3π
4.[2021·湖北五校联考] 为迎接中国共产党诞辰100周年,我校扬帆文学社举办有奖征文活动,每位获奖者的奖品为4个半径为2 cm的球形饰品,文学社的同学们为每一位获奖选手制作一个正四面体的包装盒,则包装盒的
高的最小值为________ cm.
解析:当4个球如图放置,再让正四面体包装盒的每个面与三个球相切,这样的包装盒高最小
连接4个球心,得到一个棱长为4小四面体,小四面体的中心与包装盒正四面体的中心重合,
容易求出小四面体的高,由正四面体的性质,
正四面体中心到底面的距离为高的,所以小正四面
体中心到底面的距离为,所以小四面体中心
(正四面体包装盒中心)到正四面体包装盒底面的
距离为+2,再利用正四面体性质,四面体包装盒的高为4×=+8
+8
【技法领悟】
空间几何体与球接、切问题的求解方法
(1)确定球心的位置,弄清球的半径(直径)与几何体的位置和数量关系.
(2)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(3)补成正方体、长方体、正四面体、正棱柱、圆柱等规则几何体.
微专题3
空间中的位置关系
『常考常用结论』
1.直线、平面平行的判定及其性质
(1)线面平行的判定定理:a α,b α,a∥b a∥α.
(2)线面平行的性质定理:a∥α,a β,α=b a∥b.
(3)面面平行的判定定理:a β,b β,a=P,a∥α,b∥α α∥β.
(4)面面平行的性质定理:α∥β,α=a,β=b a∥b.
2.直线、平面垂直的判定及其性质
(1)线面垂直的判定定理:m α,n α,m=P,l⊥m,l⊥n l⊥α.
(2)线面垂直的性质定理:a⊥α,b⊥α a∥b.
(3)面面垂直的判定定理:a β,a⊥α α⊥β.
(4)面面垂直的性质定理:α⊥β,α=l,a α,a⊥l a⊥β.
『保分题组训练』
1.[2021·山东潍坊一模]在空间中,下列命题是真命题的是( )
A.经过三个点有且只有一个平面
B.平行于同一平面的两直线相互平行
C.如果两个角的两条边分别对应平行,那么这两个角相等
D.如果两个相交平面垂直于同一个平面,那么它们的交线也垂直于这个平面
解析:A没有说清楚三点是否共线,B明显错误,C中这两个角也有可能互补.
故选D.
D
2.[2021·河北衡水中学第二次联考]已知a,b为两条不同的直线,α,β为两个不同的平面,则下列结论正确的是( )
A.若α∥β,a α,b β,则a∥b
B.若a α,b β,a∥b,则α∥β
C.若α=a,b β,b⊥a,则α⊥β
D.若α=l,α⊥β,a α,a⊥l,a∥b,则b⊥β
解析:对于A,如图,在长方体ABCD-A1B1C1D1中,平面A1B1C1D1∥平面ABCD,A1B1 平面A1B1C1D1,AC 平面ABCD,但A1B1与AC不平行,故A错误;对于B,如图,A1B1 平面A1B1BA,DC 平面ABCD,A1B1∥DC,但平面A1B1BA与平面ABCD不平行,故B错误;对于C,如图,平面ABC1D1∩平面ABCD=AB,BC 平面ABCD,且BC⊥AB,但平面ABCD与平面ABC1D1不互相垂直,故C错误;对于D,由平面与平面垂直的性质定理,得a⊥β,又a∥b,所以b⊥β,故D正确.
故选D.
D
3.[2021·河北张家口一模]已知两条不同的直线l,m和不重合的两个平面α,β,且l⊥β,有下面四个命题:
①若m⊥β,则l∥m;②若α∥β,则l⊥α;
③若α⊥β,则l∥α;④若l⊥m,则m∥β.
其中真命题的序号是( )
A.①② B.②③ C.②③④ D.①④
解析:对于①,由l⊥β,m⊥β,可得l∥m,故①正确;
对于②,若l⊥β,α∥β,可得l⊥α,故②正确;
对于③,若l⊥β,α⊥β,则l∥α或l α,故③错误;
对于④,若l⊥β,l⊥m,则m∥β或m β,故④错误.
综上,真命题的序号是①②.
故选A.
A
4.[2021·山东泰安一模](多选题)如图所示,在长方体,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中成立的是( )
A.EF与BB1垂直
B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°
D.EF∥平面A1B1C1D1
ABD
解析:连接A1B,A1C1,则A1B交AB1于E,又F为BC1中点,
可得EF∥A1C1,由B1B⊥平面A1B1C1D1,可得B1B⊥A1C1,可得B1B⊥EF,故A正确;
连接D1B1,EF∥A1C1,A1C1⊥平面BDD1B1,可得EF⊥平面BDD1B1,故B正确;
EF与C1D所成角就是∠A1C1D,∵AA1的长度不确定,∴∠A1C1D的大小不确定,故C错误;
由E,F分别是AB1,BC1的中点,得EF∥A1C1,可得EF∥平面A1B1C1D1,故D正确.
故选ABD.
【技法领悟】
空间位置关系的判断方法
1.根据空间线面平行、垂直关系的判定定理和性质定理逐项判断来解决问题;
2.必要时可以借助空间几何模型,如从长方体、四面体等模型中观察线面位置关系,并结合有关定理来进行判断.
[提醒]
1.平面几何中的结论不能完全引用到立体几何中;
2.当从正面入手较难时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断.
第1讲 空间几何体与空间位置关系——小题备考
微专题1 空间几何体的表面积和体积
微专题2 与球有关的切、接问题
微专题3 空l间中的位置关系
微专题1
空间几何体的表面积和体积
『常考常用结论』
1.柱体、锥体、台体、球的表面积公式:
①圆柱的表面积S=2πr(r+l);
②圆锥的表面积 S=πr(r+l);
③圆台的表面积S=π(r′2+r2+r′l+rl);
④球的表面积S=4πR2.
2.柱体、锥体和球的体积公式:
①V柱体=Sh(S为底面面积,h为高);
②V锥体=Sh(S为底面面积,h为高);
③V球=πR3.
『保分题组训练』
1.[2021·广东大联考]正方体ABCD-A1B1C1D1的棱长为2,E为BC的中点,则四面体AEDC1的体积为( )
A.4 B. C. D.2
C
解析:由题意,四面体AEDC1的底面积为:×2×2=2,高为2,
所以四面体AEDC1的体积为:×2×2=.
故选C.
2.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12π B.12π C.8π D.10π
B
解析:设圆柱的底面半径为r,由题意得高h=2r,
∴(2r)2=8,得r=,
∴S圆柱表=2πr2+2πrh=4π+8π=12π.故选B.
3.[2021·福建福州二模]某公园设置了一些石凳供大家休息,每张石凳是由正方体石料截去八个一样的四面体得到的,如图所示.如果一张石凳的体积是0.18 m3,那么原正方体石料的体积是( )
A.0.196 m3 B.0.216 m3
C.0.225 m3 D.0.234 m3
解析:设正方体的棱长为a,则正方体的体积为a3,
每一个正四面体的体积为:····=,
由题意可知:a3-8·=0.18 a3=0.216,故选B.
B
4.[2021·山东淄博一模]已知某圆锥底面圆的半径r=1,侧面展开图
是一个半圆,则此圆锥的体积为________.
解析:∵圆锥的侧面展开图是一个半圆,圆锥的底面周长为:2π,即侧面展开图半圆的弧长是2π,半圆的半径就是圆锥的母线:2,
圆锥的高为:=,
∴圆锥的体积=π·12·=.
『提分题组训练』
1. [2021·湖北五校联考]某班科技兴趣小组研究在学校的图书馆顶上安装太阳能板的发电量问题,要测量顶部的面积,将图书馆看成是一个长方体与一个等底的正四棱锥组合而成,经测量长方体的底面正方形的边长为26米,高为9米,当正四棱锥的顶点在阳光照射下的影子恰好落在底面正方形的对角线的延长线上时,测的光线与底面夹角为30°,正四棱锥顶点的影子到长方体下底面最近顶点的距离为11.8米,则图书馆顶部的面积大约为________平方米(注:≈1.4,≈1.7,≈15.2)( )
A.990 B.890 C.790 D.690
C
解析:如图1,根据题意得:∠PSO=30°,CC1=9,SC1=11.8,AB=26,
所以C1O=13≈18.2,故SO=SC1+C1O=11.8+18.2=30,
故在Rt△PSO中,设PO=x,则PS=2x,SO=30,
所以2+2=2,即:900+x2=4x2,解得x=10≈17
所以如图2,在正四棱锥P-ABCD中,PO′=17-9=8,AB=26,
取BC中点E,连接EP,EO′,所以EO′=13
由正四棱锥的性质得△PEO为直角三角形,故2=2+2=132+82=233,
所以=≈15.2,
所以正四棱锥P-ABCD的侧面积为S=4×S△PBC=4××15.2×26=790.4≈790.故选C.
2.[2021·湖南永州三模] 有一个装有水且底面直径为12 cm的圆柱形容器,水面与容器口的距离为1 cm.现往容器中放入一个半径为r(单位:cm)的小球,该小球放入水中后直接沉入容器底部,若使该容器内的水不溢出,则小球半径r的最大值为( )
A.1 B. 2 C. 3 D. 4
解析:小球放入水中后直接沉入容器底部,若使该容器内的水不溢出,则球的最大体积与圆柱上部的体积相等,小球半径r,
可得·r3=62π·1,
解得r=3(cm).故选C.
C
3.[2021·辽宁沈阳三模]柏拉图多面体,是指严格对称,结构等价的正多面体,由于太完美,因此数量很少,只有正四、六、八、十二、二十面体五种,如果用边数不同的正多边形来构造接近圆球、比较完美的多面体,那么数量会多一些,用两种或两种以上的正多边形构建的凸多面体虽不是正多面体,但有些类似,这样的多面体叫做半正多面体,古希腊数学家、物理学家阿基米德对这些正多面体进行研究并发现了13种半正多面体(后人称为“阿基米德多面体”).现在正四面体上将四个角各截去一角,形成最简单的阿基米德多面体家族中的一个,又名截角四面体.设原正四面体的棱长为6,则所得的截角四面体的体积为( )
A. B. C. D.18
C
解析:由题意及几何体的对称性可知,所得截角四面体为棱长为6的正四面体截掉四个棱长为2的正四面体而构成的几何图形.设一个棱长为x的正四面体的体积为V(x),可求得正四面体的高为=x,正四面体一个底面正三角形的面积为x2sin 60°=x2,V(x)=x×x2=x3.可得V(6)=×216=18,V(2)=×8=,故所得截角四面体的体积为18-4×=.故选C.
4.[2021·河北沧州二模]沙漏是一种古代的计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时,如图,某沙漏由上、下两个圆锥组成,该圆锥的高为1,若上面的圆锥中装有高度为的液体,且液体能流入下面的圆锥,
则液体流下去后的液面高度为________.
解析:=3=,当液体流下去后,=1-=,所以液体流下去后的液面高度为1-.
1-
【技法领悟】
求解几何体的表面积和体积的技巧
1.求几何体的表面积及体积问题,可以多角度、多方位地考虑,熟记公式是关键.求三棱锥的体积,等体积转化是常用的方法,转化原则是其高易求,底面放在已知几何体的某一面上.
2.求不规则几何体的体积,常用分割或补形的方法,将不规则几何体转化为规则几何体,易于求解.
微专题2
与球有关的切、和接的问题
『常考常用结论』
1.球的表面积S=4πR2,体积V=πR3.
2.长方体、正方体的体对角线等于其外接球的直径.
3.n面体的表面积为S,体积为V,则内切球的半径r=.
4.直三棱柱的外接球半径:R=,其中r为底面三角形的外接圆半径,L为侧棱长,如果直三棱柱有内切球,则内切球半径R′=.
5.正四面体中,外接球和内切球的球心重合,且球心在高对应的线段上,它是高的四等分点,球心到顶点的距离为外接球的半径R=a,球心到底面的距离为内切球的半径r=a,因此R∶r=3∶1.
『保分题组训练』
1.[2020·天津卷]若棱长为2的正方体的顶点都在同一球面上,则该球的表面积为( )
A.12π B.24π C.36π D.144π
解析:设外接球的半径为R,易知2R=×2=6,所以R=3,于是表面积S=4πR2=36π,故选C.
C
2.设正方体的表面积为24,那么其内切球的体积是( )
A. B.π C. D.
解析:设正方体的棱长为a,
则6a2=24,解得a=2,
所以正方体的内切球的半径为1,
其体积为×13=.
故选A.
A
3.[2021·山东泰安一模]设三棱柱的侧棱垂直于底面,所有棱的长都为1,顶点都在一个球面上,则该球的表面积为( )
A.5π B.π C.π D.π
解析:根据题意条件可知三棱柱是棱长都为1的正三棱柱,上下底面中心连线的中点就是球心,
则其外接球的半径为R==,
则球的表面积为S=4π×=,
故选D.
D
4.[2021·辽宁朝阳二模]已知三棱锥S-ABC的三条侧棱SA,SB,SC两两互相垂直且AC=,AB=,此三棱锥的外接球的表面积为14π,则BC=_______.
4.解析:设SA=x,SB=y,SC=z,
由题意可得:x2+z2=13,x2+y2=5,y2+z2=BC2,
三棱锥的外接球的表面积为14π,三棱锥扩展为长方体,长方体的对角线的长度,就是外接球的直径2R,
所以2R=,4πR2=14π,
可得x2+y2+z2=14,
解得x=2,y=1,z=3,
所以BC==.
『提分题组训练』
1.[2021·山东临沂二模]如图为一个圆锥形的金属配件,重75.06克,其正视图是一个等边三角形,现将其打磨成一个体积最大的球形配件,则该球形配件的重量约为( )
A.32.69克 B.33.36克 C.34.03克 D.34.37克
解析:设圆锥形的体积为V1,底面半径为r,内切球的体积为V2,
∴V1=··2r,V2=π3,
∴= = m=33.36,
故选B.
B
2.[2021·河北沧州二模]在三棱锥P-ABC中,底面ABC是面积为3的正三角形,若三棱锥P-ABC的每个顶点都在球O的球面上,且点O恰好在平面ABC内,则三棱锥P-ABC体积的最大值为( )
A. B.2 C.4 D.6
解析:由题可知底面ABC的边长为2,因为三棱锥P-ABC外接球的球心O恰好在平面ABC内,所以球O的半径为2,则三棱锥P-ABC体积的最大值为×3×2=2.
故选B.
B
3.[2021·山东德州一模]已知三棱锥P-ABC中,AP,AB,AC三条棱两两垂直,且长度均为2,以顶点P为球心,4为半径作一个球,则该球面被三棱锥四个表面截得的所有弧长之和为________.
解析:如图,AP=2,PN=4,则AN=2,∠APN=,
∴∠NPM==,
∴=×4=,同理=,
=×2=π,=×4=,
故球面与三棱锥的表面相交所得到的四段弧长之和等于+π+=3π,
3π
4.[2021·湖北五校联考] 为迎接中国共产党诞辰100周年,我校扬帆文学社举办有奖征文活动,每位获奖者的奖品为4个半径为2 cm的球形饰品,文学社的同学们为每一位获奖选手制作一个正四面体的包装盒,则包装盒的
高的最小值为________ cm.
解析:当4个球如图放置,再让正四面体包装盒的每个面与三个球相切,这样的包装盒高最小
连接4个球心,得到一个棱长为4小四面体,小四面体的中心与包装盒正四面体的中心重合,
容易求出小四面体的高,由正四面体的性质,
正四面体中心到底面的距离为高的,所以小正四面
体中心到底面的距离为,所以小四面体中心
(正四面体包装盒中心)到正四面体包装盒底面的
距离为+2,再利用正四面体性质,四面体包装盒的高为4×=+8
+8
【技法领悟】
空间几何体与球接、切问题的求解方法
(1)确定球心的位置,弄清球的半径(直径)与几何体的位置和数量关系.
(2)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(3)补成正方体、长方体、正四面体、正棱柱、圆柱等规则几何体.
微专题3
空间中的位置关系
『常考常用结论』
1.直线、平面平行的判定及其性质
(1)线面平行的判定定理:a α,b α,a∥b a∥α.
(2)线面平行的性质定理:a∥α,a β,α=b a∥b.
(3)面面平行的判定定理:a β,b β,a=P,a∥α,b∥α α∥β.
(4)面面平行的性质定理:α∥β,α=a,β=b a∥b.
2.直线、平面垂直的判定及其性质
(1)线面垂直的判定定理:m α,n α,m=P,l⊥m,l⊥n l⊥α.
(2)线面垂直的性质定理:a⊥α,b⊥α a∥b.
(3)面面垂直的判定定理:a β,a⊥α α⊥β.
(4)面面垂直的性质定理:α⊥β,α=l,a α,a⊥l a⊥β.
『保分题组训练』
1.[2021·山东潍坊一模]在空间中,下列命题是真命题的是( )
A.经过三个点有且只有一个平面
B.平行于同一平面的两直线相互平行
C.如果两个角的两条边分别对应平行,那么这两个角相等
D.如果两个相交平面垂直于同一个平面,那么它们的交线也垂直于这个平面
解析:A没有说清楚三点是否共线,B明显错误,C中这两个角也有可能互补.
故选D.
D
2.[2021·河北衡水中学第二次联考]已知a,b为两条不同的直线,α,β为两个不同的平面,则下列结论正确的是( )
A.若α∥β,a α,b β,则a∥b
B.若a α,b β,a∥b,则α∥β
C.若α=a,b β,b⊥a,则α⊥β
D.若α=l,α⊥β,a α,a⊥l,a∥b,则b⊥β
解析:对于A,如图,在长方体ABCD-A1B1C1D1中,平面A1B1C1D1∥平面ABCD,A1B1 平面A1B1C1D1,AC 平面ABCD,但A1B1与AC不平行,故A错误;对于B,如图,A1B1 平面A1B1BA,DC 平面ABCD,A1B1∥DC,但平面A1B1BA与平面ABCD不平行,故B错误;对于C,如图,平面ABC1D1∩平面ABCD=AB,BC 平面ABCD,且BC⊥AB,但平面ABCD与平面ABC1D1不互相垂直,故C错误;对于D,由平面与平面垂直的性质定理,得a⊥β,又a∥b,所以b⊥β,故D正确.
故选D.
D
3.[2021·河北张家口一模]已知两条不同的直线l,m和不重合的两个平面α,β,且l⊥β,有下面四个命题:
①若m⊥β,则l∥m;②若α∥β,则l⊥α;
③若α⊥β,则l∥α;④若l⊥m,则m∥β.
其中真命题的序号是( )
A.①② B.②③ C.②③④ D.①④
解析:对于①,由l⊥β,m⊥β,可得l∥m,故①正确;
对于②,若l⊥β,α∥β,可得l⊥α,故②正确;
对于③,若l⊥β,α⊥β,则l∥α或l α,故③错误;
对于④,若l⊥β,l⊥m,则m∥β或m β,故④错误.
综上,真命题的序号是①②.
故选A.
A
4.[2021·山东泰安一模](多选题)如图所示,在长方体,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中成立的是( )
A.EF与BB1垂直
B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°
D.EF∥平面A1B1C1D1
ABD
解析:连接A1B,A1C1,则A1B交AB1于E,又F为BC1中点,
可得EF∥A1C1,由B1B⊥平面A1B1C1D1,可得B1B⊥A1C1,可得B1B⊥EF,故A正确;
连接D1B1,EF∥A1C1,A1C1⊥平面BDD1B1,可得EF⊥平面BDD1B1,故B正确;
EF与C1D所成角就是∠A1C1D,∵AA1的长度不确定,∴∠A1C1D的大小不确定,故C错误;
由E,F分别是AB1,BC1的中点,得EF∥A1C1,可得EF∥平面A1B1C1D1,故D正确.
故选ABD.
【技法领悟】
空间位置关系的判断方法
1.根据空间线面平行、垂直关系的判定定理和性质定理逐项判断来解决问题;
2.必要时可以借助空间几何模型,如从长方体、四面体等模型中观察线面位置关系,并结合有关定理来进行判断.
[提醒]
1.平面几何中的结论不能完全引用到立体几何中;
2.当从正面入手较难时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断.
同课章节目录
